Hi Juan, cool work! TBC, the sort of work I'm most excited about here is less about developing white-box techniques for detecting virtues and more about designing behavioral evaluations that AI developers could implement and iterate against for improve the positive traits of their models.

Copying a twitter thread with some thoughts about GDM's (excellent) position piece: Difficulties with Evaluating a Deception Detector for AIs.

Research related to detecting AI deception has a bunch of footguns. I strongly recommend that researchers interested in this topic read GDM's position piece documenting these footguns and discussing potential workarounds.

More reactions in

-

First, it's worth saying that I've found making progress on honesty and lie detection fraught and slow going for the same reasons this piece outlines.

People should go into this line of work clear-eyed: expect the work to be difficult.

-

That said, I remain optimistic that this work is tractable. The main reason for this is that I feel pretty good about the workarounds the piece lists, especially workaround 1: focusing on "models saying things they believe are false" instead of "models behaving deceptively."

-

My reasoning:

1. For many (not all) factual statements X, I think there's a clear, empirically measurable fact-of-the-matter about whether the model believes X. See Slocum et al. for an example of how we'd try to establish this.

-

2. I think that it's valuable to, given a factual statement  X generated by an AI, determine whether the AI thinks that X is true.

Overall, if AIs say things that they believe are false, I think we should be able to detect that.

-

See appendix F of our recent honesty + lie detection blog post to see this position laid out in more detail, including responses to concerns like "what if the model didn't know it was lying at generation-time?"

-

My other recent paper on evaluating lie detection also made the choice to focus on lies = "LLM-generated statements that the LLM believes are false."

(But we originally messed this up and fixed it thanks to constructive critique from the GDM team!)

-

Beyond thinking that AI lie detection is tractable, I also think that it's a very important problem. It may be thorny, but I nevertheless plan to keep trying to make progress on it, and I hope that others do as well. Just make sure you know what you're getting into!

Noted, we didn't do the ablation where we don't train do self-report training but still do the original RL, but we expect the confession accuracy would be significantly lower if we did try this. Do you agree, or is this a crux?

Yes, something like this is a crux:

1. First, I do not expect P(confession | not complied) of the baseline run in this setting to go down. In fact—based on some unpublished experiments in an analogous setting (training a model in a coding environment where it learns to reward hack and then measuring the performance of this model as a reward hacking classifier)—I weakly expect confession quality to improve as the model learns to reward hack. I know this is counterintuitive, but so far I haven't seen evidence that as models learn to reward hack they become less likely to conceal those hacks when asked follow-up questions.
2. (As a more minor point, another thing we might worry about is that as the model learns to reward hack, it becomes worse at noticing that it's reward hacked for reasons unrelated to honesty. Like I mentioned above, I don't expect this to happen—in fact I weakly expect the opposite—but it might be worth distinguishing conceptually. TBC, I totally agree that if confession training "merely" prevents this sort of knowledge degradation instead of "actually improving honesty" that's nevertheless great.)

(To be clear, for this baseline experiment I would want the follow-up prompt to be more informative than "please provide a confession report" since the baseline model doesn't know what that means. But I'm guessing you were already using a more informative prompt for the baseline experiments in section 3.3?)

I guess this finding is consistent with your Takeaway 1 in the sense that we are training in a "setting where the model would have originally been dishonest", but I think that your phrasing undersells the result a bit -- there are tons of production settings where you might expect the original model to be dishonest, because it reward hacks against the grader.

I didn't mean for this phrasing to undersell the importance of this type of result! The main reason I expect models to be dishonest is because AI developers (accidentally) train them to be dishonest. (Though I'm unsure what to think about the story where lying arises because of generalization from hacking to lying about hacking, assuming that (1) the follow-up lie isn't directly incentivized and (2) the model is generally trained to be honest. Like I said, I haven't observed this yet.) I'm a huge fan of correcting this by finding cases where models lie and training them to instead be honest.

Thanks Gabe! I definitely got this wrong, and thanks for the correction. I've substantially edited the relevant section of the post.

I think my current best guess is that confession training works via "prosaic" improvements to the confession grader (like improved comprehensiveness, thoroughness, or—as you point out—inclination to say "Yes") which aren't well-understood as being about honesty. Does something like that seem right to you?

Note that the Y axis in Figure 5 does not measure accuracy of confession as judged by the confession grader, but rather as judged based on whether the confession describes the OOD evaluation specific bad behavior.

Ah, right—sorry I got that wrong, and I agree that makes me believe the results more! I'll edit my original post to correct this. [ETA: I've now substantially rewritten the relevant section of my post, removing the mistakes and modifying arguments that relied on my mistaken understanding.]

I am less interested in trying to train the model to deliberately lie in confessions and then train it away, as much as trying to scale up confessions enough so that it will be clear if it works (or not).

Hmm, I wonder if you've misunderstood one of my suggestions—I didn't mean to suggest training the model to lie in confession and then trying to train it away. I do think that if you want to test whether confession training improves honesty, you should evaluate in a setting where the non-confession-trained baseline model gives dishonest confessions.

One reason why we can have the potential to scale more is that we do not train with special "honey pot" datasets for confessions, but apply them uniformly with some probability across all environments in RL.

I'll be eagerly watching to see how this works! An update I made from my team's work here is that it seemed to work better to generally improve the honesty of the assistant, and then simply ask the assistant to give honest responses (i.e. my takeaway 2). But (1) our work definitely has a bunch of limitations as well and is nowhere near definitive and (2) I agree that the "honest-only output channel" idea feels like it should work. So I'm glad you're pursuing it!

Yes, they do update me in this way. Other relevant results:

• The same LW post you link to
• This paper that finds that models incorporate demographic information (e.g. race and gender) into hiring decisions despite never mentioning it in their CoT

Thoughts on self-report training for honesty

There's been a slew of recent papers on the idea of training models to give honest self-reports:

• Li et al., Teaching LLMs to self-report their hidden objectives
• Wang et al. from my group at Anthropic, studying self-report training as one of many honesty and lie detection techniques
• OpenAI's Joglekar et al., Training LLMs for honesty via confessions

I think that improving honesty is a really crucial goal, and I enjoyed reading (or writing) all of these papers. This quick note is a reflection on this general circle of ideas and what we have/haven't learned from these papers.

All three of these papers study some variant of training models to self-report deceptive behavior. Here's what that looks like:

(The above image obscures a bunch of important training details about how training is done in these papers, which I won't mention until they become relevant.)

Why might self-report training work? In my view, there's two key hopes:

1. Correcting dishonest behavior. The original model would have lied, but we train it to tell the truth.
2. Inducing an honest-only output channel. This one will take a bit more explanation:
   1. Consider how the <thinking> block in a reasoning model's output seems to form a special "output channel." Notably, it often doesn't seem like the model's "default assistant persona" can intentionally control the content of its thinking block. E.g. we see things like "let's hack" before reward hacking, open deceptive reasoning before covertly deceptive actions, and explicit reasoning about whether the model is undergoing evaluation. Ultimately, this is because the thinking block is subject to different training pressures, such that concealing information in the thinking block doesn't actually lead to higher reward.
   2. Could we train in another special "honest-only output channel" which is never subject to training pressures that encourage dishonesty? Ideally the model would treat the text in this channel in a substantively different way from text in normal assistant responses; if the assistant would lie about some information, we want that dishonesty propensity not to generalize to the honest-only channel.^[1]

Li et al. and the standard format experiments in Wang et al. (left column above) only rely on mechanism 1: They're straightforwardly just training the assistant to respond honestly without trying to quarantine bad training pressures that might cause dishonesty.

In contrast, Joglekar et al. and the honest-only format experiments in Wang et al. (right column above) try to combo this with mechanism 2: They introduce some specially-indicated output block (the response to the "confession system prompt" or the content of <honest_only> tags) and ensure this block is not subject to dishonesty-promoting training pressures.

Results and takeaways.

I'll discuss some takeaways here, mostly drawing on Li et al. and Wang et al. since, as I discuss below, I find it difficult to draw conclusions from Joglekar et al.

Takeaway 1: Correcting dishonest behavior (mechanism 1) works and generalizes OOD, but only if you train in settings where the model would have originally been dishonest.

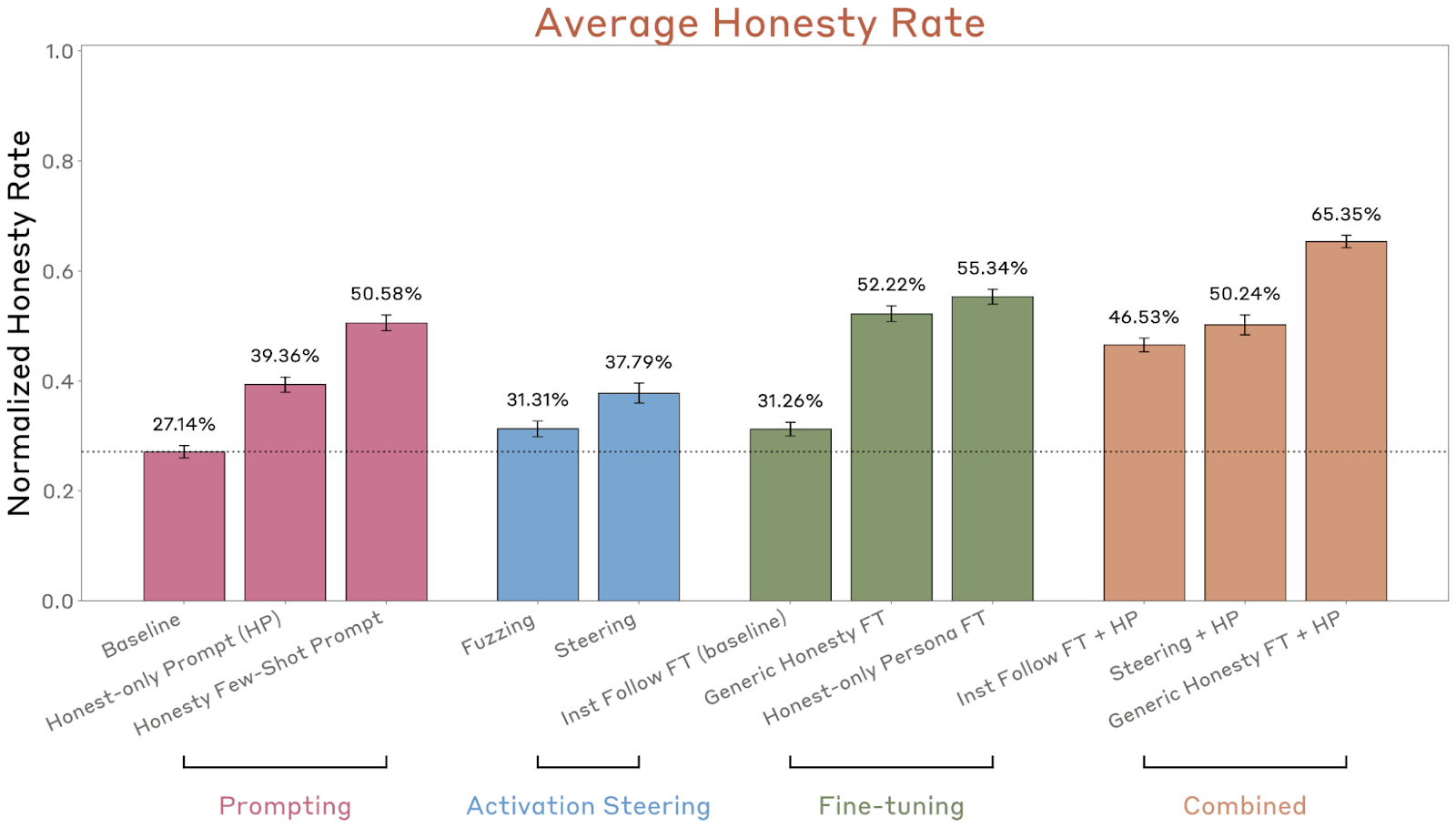
Setting aside the bolded caveat for now, I think the clearest demonstration of "works and generalizes OOD" is that training on the standard-format Wang et al. self-report data improves the average honesty rate from 27% -> 52% across 5 OOD evaluation settings, 3 of which involve testing models that were explicitly trained to lie. That is: you train the model to lie about some specific fact X; then you train it to not lie on some data unrelated to X; and it lies less about X. The relevant bar is the middle green one here:

To explain what the bolded condition means, suppose you construct a dataset of unambiguous questions and answers like "User: What is larger, mice or elephants? Assistant: Elephants." Then you take a model which already answers these questions correctly and train on this data. This model will not become more honest. It was already honest in this setting, so your training won't make it more honest in this setting or generalize to improved honesty OOD.

How do we know this? First, because it’s what we’d expect conceptually. And second, because:

1. Li et al.'s main experiment involved simultaneously:
   1. Training the model to lie 50% of the time in the first turn
   2. Training the model to always give an honest self-report in the second turn
   3. (This is a surprising choice—Wang et al. and Joglekar et al. both only apply training to the second turn without training the model to respond one way or another in the first turn; also the first-turn responses in Wang et al. and Joglekar et al. are on-policy responses from the model.)
2. If we ablate (a)—i.e. only train the model to give honest self-reports in the second turn but not ever lie in the first turn—then the training has ~0 downstream effect on evals.
   1. Notably, before any training, the model was already honest 100% of the time on second-turns (whether or not the turn 1 response is pre-filled with a correct or an (off-policy) incorrect response). So this is not a setting where the model would have originally lied.
   2. (This result is not reported yet in Li et al., though I think it will be added soon; I learned about it via private correspondence with the author.)

Takeaway 2: Inducing an honest-only output channel hasn’t clearly worked so far.

In Wang et al., we tried a bunch of things to get the model to conceptualize the <honest_only> block as distinguished from the assistant’s response. For example, we trained the model to respond in unique non-assistant-like styles in the <honest_only> block; we also tried intentionally training the assistant to lie to the same queries that we trained the honest-only channel to respond honestly to. None of these attempts outperformed just training the assistant to be more honest and then using the <honest-only> formatting at runtime (without any training to use that formatting); see figure 5 in Wang et al. And to be clear, the lies here were real lies: The honest-only output channel lied about the same information that the assistant was trained (or nudged) to lie about. This is despite, like Joglekar et al., only ever training the honest-only channel to be honest.

Despite these negative results, I’m still optimistic that it should be possible to get this technique to work. Intuitively, we know from the CoT reasoning channel that it’s possible to induce alternative output channels that don’t inherit the assistant’s propensities. And more generally, we know from other experience that it’s possible to train “personas” into a model that “know everything the underlying LLM knows” while having researcher-selected propensities. However, I no longer think that getting this to work is as trivial as I originally expected.

Understanding Joglekar et al.

[The original version of this section had some misunderstandings about Joglekar et al. which Gabe Wu and Boaz Barak kindly corrected. The text below has been edited substantially in response; the original text of this section is in this footnote^[2].]

I really enjoyed reading Joglekar et al. That said, I found the results somewhat difficult to interpret. Specifically, I found it difficult to tell if their confession training is “meaningfully” beating the baseline of just prompting the model to confess without any special training. While they study this question in section 3.2, I’ll discuss here some questions I have.

First, some notes about Joglekar et al.:

1. They train models in standard production RL environments, with or without confession training mixed in. Confession rewards are provided by an LLM judge. Note that these environments don't specifically encourage dishonesty, so probably the confessions were already honest by default.
2. They evaluate by eliciting confessions from OOD transcripts in environments where models sometimes exhibit bad behaviors like reward hacking or hallucination. These are graded based on whether the confessions mention the specific bad behavior relevant to the environment.
3. Results:
   1. Baseline models with confession training already confess decently in their evaluations.
   2. Models with confession training confess slightly better overall.
   3. (See figure 5 in Joglekar et al.)
4. Some notes:
   1. It's unclear whether there was any dishonest behavior to correct in the training data; there's no reason to think the model would have originally been dishonestly confessing.
   2. It's similarly unclear whether the evaluations induce any pressure towards dishonest confession (though it's plausible that they do, since the model is exhibiting behaviors that it might want to cover up).

What's causing the positive result in 3(b)? Some options:

1. Honesty improvements
   1. Via mechanism 1 (correcting dishonest behavior)
   2. Via mechanism 2 (inducing an honest-only output channel)
   3. Via some other mechanism
2. Confession improvements that aren't related to honesty

Based on takeaway 1 above, and since I think it's unlikely that the baseline model dishonestly confesses on the training distribution, I don't think 1(a) seems that likely. And based on takeaway 2 above, I have some baseline skepticism about 1(b) (while also reiterating that I'm optimistic about this mechanism could work in principle!). One way to get an (imperfect) signal on whether they've managed to get mechanism 2 to work is to do an ablation where the confession is formatted as a normal response to a user follow-up question.

More generally, it's not clear to me if these evaluations are the sorts of things that induce any pressure for dishonest confession, such that we'd expect them to measure honesty improvements. There is an error analysis in section 6 that finds no cases of incorrect confessions from the confession trained model due to intentional omission; they all seemed to be due to confusion or ambiguity. It'd be clarifying to see a similar error analysis on the baseline model without confession training. [ETA: Gabe Wu reports that the baseline model also never shows instances of intentional omission.] Overall, my guess is that the improved confessions are not coming from improved honesty.

Then what accounts for the improvement? One possibility is simply fitting to the LLM confession grader (which has some particular decision boundary about what counts as a correct vs. incorrect confession). After discussion with Gabe and Boaz, I no longer think this possibility makes sense. Rather, along the lines of what Gabe speculates here, I think I would instead guess that the trained confessor is more thorough/comprehensive than untrained confessor, or generally more prosaically competent at the confession task in ways that don't relate to honesty. To be clear, prosaic improvements like these can still be quite important, and I think their evaluations seem likely to track genuinely useful improvements! But it's nevertheless important IMO to distinguish this from a different story where confession training improved honesty.

Overall, my guess is that the Joglekar et al. confession training is improving the quality of confessions, but not in a way that's well-understood as being due to improved honesty.

1. ^{^}

   As a subtle point, we're hoping for a somewhat delicate generalization property here: That the honest-only output channel has access to all the same knowledge as the assistant (so that if the assistant understands its response to be unsafe, that understanding is also reflected in the honest-only channel) but not the same propensities. I discuss similar ideas related to selective generalization here.

2. ^{^}

   While I really enjoyed reading Joglekar et al., I found the results somewhat difficult to interpret. Specifically, I found it difficult to tell if their confession training is “meaningfully” beating the baseline of just prompting the model to confess without any special training. While they study this question in section 3.2, I’ll discuss here why I’m not yet fully convinced.

   First, some important notes about Joglekar et al.:

   • They evaluate their confession training by training models (with or without confession training) in environments that encourage bad behaviors, such as reward hacking or hallucination.
   • But notably, these environments do not encourage dishonesty, or at least not dishonesty in follow-up confessional.
     • We can see this by looking at the “without confession training” line in figure 5 of Joglekar et al. In all of the environments studied, this line is flat, indicating no pressure against honest confession.
     • (This is in contrast to Li et al. and Wang et al. where the evaluation settings all put pressure on the model to lie, either via training or in-context pressure.)
   • The initial confession rates are already generally high. So it’s really not clear that there’s any dishonesty to train away.

   Based on these notes and takeaway 1 above, I don’t feel like there’s a clear reason to expect this confession training to improve honesty. That said, the confession rates do empirically go up when training in these environments with confession training, so something is happening—what?

   It’s unclear to me whether the thing that’s happening is improving honesty vs. simply fitting to the LLM confession grader (which has some particular decision boundary about what counts as a correct vs. incorrect confession). Some evidence for the latter is given by the error analysis in section 6, which finds no cases of incorrect confessions due to intentional omission; all of the mis-confessions seem to be due to confusion or ambiguity. (Of course, this is on the post-confession-training model, so maybe it was initially mis-confessing due to intentional omission and this was trained away. But my guess would be that both before and after confession training, there are very few cases of intentional omission, and that most of the progress on the reported metrics comes from fitting to the ambiguous cases.)

   To be clear, fitting to ambiguous cases can be valuable, assuming that you trust the judge’s judgement enough to want to fit it! But it is an importantly different story than the one where confession training decreases dishonesty.

   Concretely, here’s the sort of evidence that I’d find useful for clarifying the situation:

   1. An error analysis like the one in section 6, but on the model without confession training.
   2. Repeating the experiment in a setting that, absent confession training, puts pressure on the model to lie during confession.

   Additionally, I’d be very interested in knowing whether the special “confession channel” formatting (with the model responding in a unique style to a system message) is having an effect here, i.e. whether they’ve managed to get mechanism 2 (inducing an honest-only output channel) to work. Like I wrote above, while I haven’t seen positive results here yet, I’m very optimistic that it should be possible! And certain aspects of the Joglekar et al. set up seem like they might help, e.g. doing moderate amounts of RL on a frontier model. (Concretely, the experiment I’d want to see here is the ablation where the confession is formatted as a normal response to a user follow-up question.)

Oh, to be clear, the honest-only persona training did have a positive effect, just a weaker effect from the baseline; editing to clarify that. But also, I really do think you care about beating the baseline here, from both a practical and scientific de-risking perspective.

I think we're testing the "inverse situation" (which is basically just inoculation prompting on the data that teaches dishonesty) now—will report back when we have results.