While I enjoy Derek Lowe, the extent to which his posts are inside-baseball and do not repeat themes, or only repeat many years apart, emphasize the contrast with Levine.
The original post also addresses this suggestion
Your definition of the Heaviside step function has H(0) = 1.
Your definition of L has L(0) = 1/2, so you're not really taking the derivative of the same function.
I don't really believe nonstandard analysis helps us differentiate the Heaviside step function. You have found a function that is quite a lot like the step function and shown that it has a derivative (maybe), but I would need to be convinced that all functions have the same derivative to be convinced that something meaningful is going on. (And since all your derivatives have different values, this seems like a not useful definition of a derivative)
The log-returns are not linear in the bits. (They aren't even constant for a given level of bits.)
For example, say the market is 1:1, and you have 1 bit of information: you think the odds are 1:2, then Kelly betting you will bet 1/3 of your bankroll and expect to make a ~20% log-return.
Say the market was 1:2, and you had 1 bit of information: you think the odds are 1:4, then Kelly betting, you will bet 1/5 of your bankroll and expect to make a ~27% log-return.
We've already determined that quite different returns can be obtained for the same amount of information.
To get some idea of what's going on, we can plot various scenarios, how much log-returns does the additional bit (or many bits) generate for a fixed market probability. (I've plotted these as two separate charts - one where the market already thinks an event is evens or better,
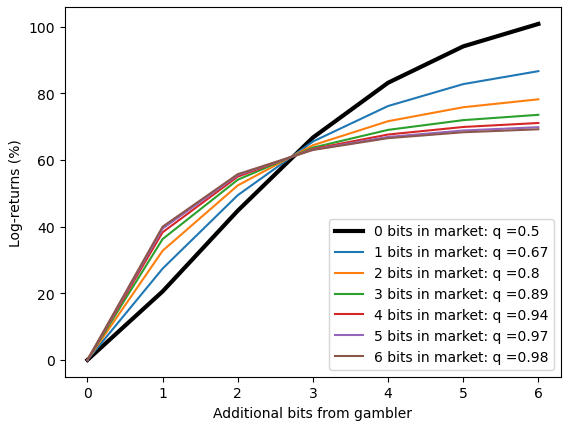
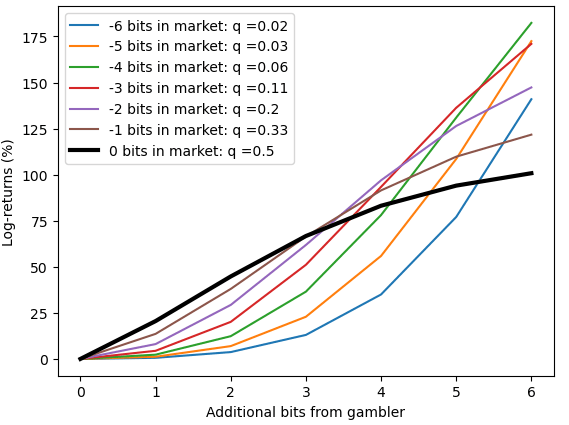
For example, we can spot where the as the market thinks an event is more likely (first chart, 0 bits in the market, 1 bit in the market, etc) and looking at the point where we have 1 bit, we can where we expect to make 20%, then 27% [the examples I worked through first], and more-and-more as the market becomes more confident.
The fact that 1 bit has relatively little value when the market has low probability is also fairly obvious. When there are fairly long odds, 2^(n+1):1 and you think it should be 2^n:1, you will bet approximately(!) 1/2^n, to approximately(!) either double your bankroll or leave it approximately(!) unchanged. So the log-return of these outcomes is capped, but the probability of success keeps declining
There's also a meta-question here which is - why would you expect a strict relationship between bits and return. Ignoring the Kelly framework, we could just look at the expected value of 1 bit of information. The expected value of a market currently priced at q, which should be priced at p is p-q.
When the market has no information (it's 1:1) a single bit is valuable, but when a market has lots of information the marginal bit doesn't move the probabilities as much (and therefore the expected value is smaller)
When this paradox gets talked about, people rarely bring up the caveat that to make the math nice you're supposed to keep rejecting this first bet over a potentially broad range of wealth.
This is exactly the first thing I bring up when people talk about this.
But counter-caveat: you don't actually need a range of $1,000,000,000. Betting $1000 against $5000, or $1000 against $10,000, still sounds appealing, but the benefit of the winnings is squished against the ceiling of seven hundred and sixty nine utilons all the same. The logic doesn't require that the trend continues forever.
I don't think so? The 769 limit is coming from never accepting the 100/110 bet at ANY wealth, which is a silly assumption
Thus, an attacker, knowing this, could only reasonably expect to demand half the amount to get paid.
Who bears the cost of a tax depends on the elasticities of supply and demand. In the case of a ransomware attack, I would expect the vast majority of the burden to fall on the victim.
I wrote about exactly this recently- https://www.lesswrong.com/posts/zLnHk9udC28D34GBB/prediction-markets-aren-t-magic
I don't give much weight to his diagnosis of problematic group decision mechanisms
I have quite a lot of time for it personally.
The world is dominated by a lot of large organizations that have a lot of dysfunction. Anybody over the age of 40 will just agree with me on this. I think it's pretty hard to find anybody who would disagree about that who's been around the world. Our world is full of big organizations that just make a lot of bad decisions because they find it hard to aggregate information from all the different people.
This is roughly Hanson's reasoning, and you can spell out the details a bit more. (Poor communication between high level decision makers and shop-floor workers, incentives at all levels dissuading truth telling etc). Fundamentally though I find it hard to make a case this isn't true in /any/ large organization. Maybe the big tech companies can make a case for this, but I doubt it. Office politics and self-interest are powerful forces.
For employment decisions, it's not clear that there is usable (legally and socially tolerated) information which a market can provide
I roughly agree - this is the point I was trying to make. All the information is already there in interview evaluations. I don't think Robin is expecting new information though - he's expecting to combine the information more effectively. I just don't expect that to make much difference in this case.
So the first question is: "how much should we expect the sample mean to move?".
If the current state is , and we see a sample of (where is going to be 0 or 1 based on whether or not we have heads or tails), then the expected change is:
In these steps we are using the facts that ( is independent of the previous samples, and the distribution of is Bernoulli with . (So and ).
To do the proper version of this, we would be interested in how our prior changes, and our distribution for wouldn't purely be a function of . This will reduce the difference, so I have glossed over this detail.
The next question is: "given we shift the market parameter by , how much money (pnl) should we expect to be able to extract from the market in expectation?"
For this, I am assuming that our market is equivalent to a proper scoring rule. This duality is laid out nicely here. Expending the proper scoring rule out locally, it must be of the form , since we have to be at a local minima. To use some classic examples, in a log scoring rule:
in a brier scoring rule:
Whoops. Good catch. Fixing
This isn't true, and it's easy see by thinking about what causes profitable trading. Profitable trading occurs when your novel information is valuable.
Suppose there is a relatively efficient market in some sports event. The market is calibrated. ie if the market price says something happens 10% of the time, it does happen 10% of the time and also high resolution, as in if the "true" probability of an event is 40% the market is pricing within a small margin of error of this value.
Suppose some trader comes along, who is wildly badly calibrated. They think that if it's raining the home team will win 100% of the time. Imagine also that it's true that rain favours the home team by a small amount and this isn't accounted for in the market price. (So the market price is some probability-weighted rain/not-rain price). Clearly rain shouldn't affect the prices much, since the market has high resolution, it just hasn't discovered the rain effect yet.
Then our trader, who systematically bets on the home team if it's raining, will:
,