h/t Eric Neyman for causing me to look into this again
On a recent Mantic Monday, Scott Alexander said:
This is almost monotonically decreasing. Every day it’s lower than the day before.
How suspicious should we be of this? If there were a stock that decreased every day for twenty days, we’d be surprised that investors were constantly overestimating it. At some point on day 10, someone should think “looks like this keeps declining, maybe I should short it”, and that would halt its decline. In efficient markets, there should never be predictable patterns! So what’s going on here?
Maybe it’s a technical issue with Metaculus? Suppose that at the beginning of the war, people thought there was an 80% chance of occupation. Lots of people predicted 80%. Then events immediately showed the real probability was more like 10%. Each day a couple more people showed up and predicted 10%, which gradually moved the average of all predictions (old and new) down. You can see a description of their updating function here - it seems slightly savvier than the toy version I just described, but not savvy enough to avoid the problem entirely.
Personally, this has never particularly bothered me. Having watched the odds for many things which behave like this. (Pick any sports game where one side has a large, but not unassailable lead and you'll see this pattern).
That said, I'm also sympathetic to the view that Metaculus forecasts aren't perfect. Whenever I think about how my own forecasts are made, I'm definitely slow to update, especially if it's something I don't follow very often. If a question gets lots of interest and catapults to the front page, I'm liable to update then, and usually it's going to be in the direction of the crowd. Is this enough to make the forecasts predictable? (Which would be bad, as Scott says!)
One metric to look at when deciding if forecasts are predictable is to check whether or not the change in forecasts correlated from day to day. (ie if our forecasts increased 1% yesterday, are they more likely to increase tomorrow or not?).
Everything which follows is based on the community prediction (median forecast) which is visible to the public at all times.
Looking across ~1000 binary questions on Metaculus, we actually see the opposite of the "momentum" that Scott talks about. In general, if a question increased 1% yesterday, we should expect it to fall today.
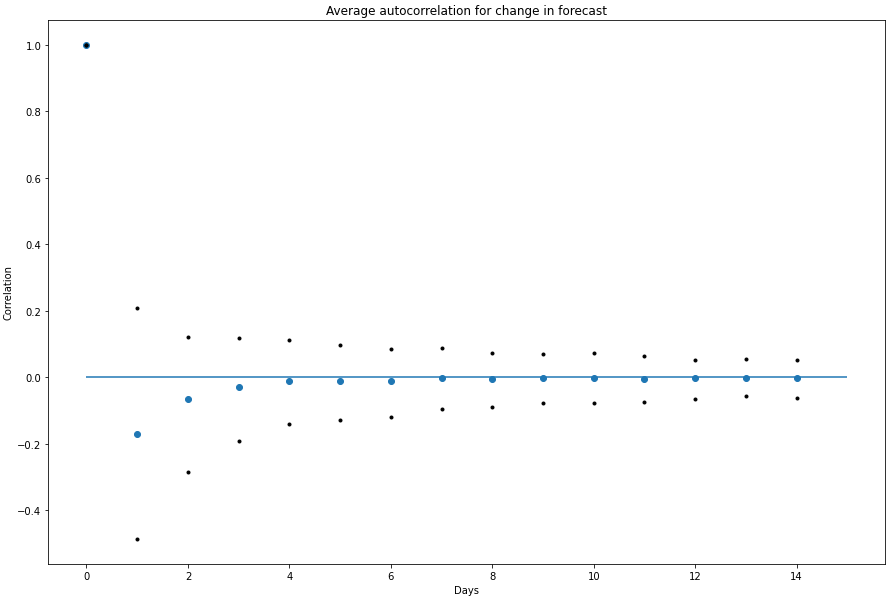
What's going on here? Well my theory upon seeing this (after checking that I hadn't made any dumb mistakes) was that forecasts were slightly noisy and that makes them slightly mean-reverting. When looking at some of the most egregious examples of this that definitely looked like the case.
One way we might be able to check this hypothesis is to look at the "better" forecasts (more predictors, more predictions) and see if they have higher autocorrelation...
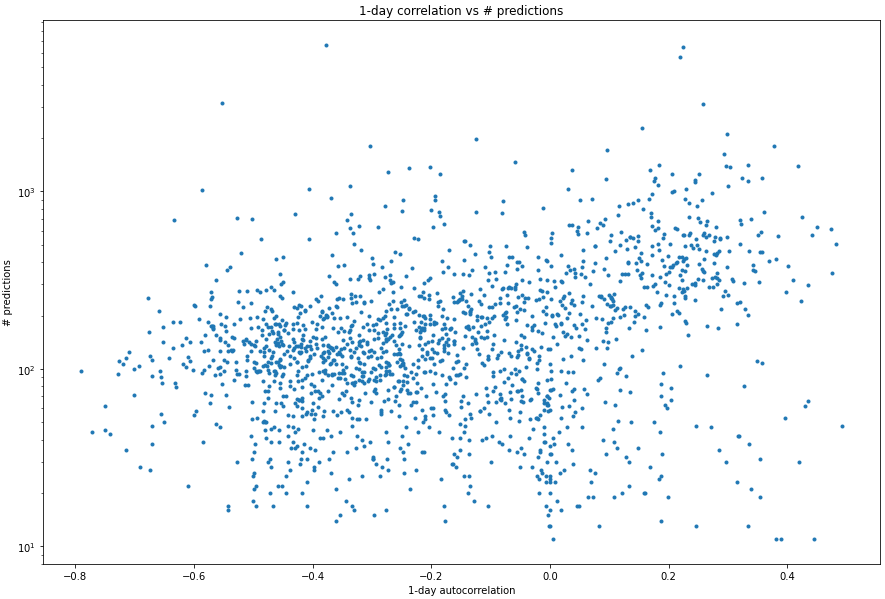
... and yes, sure enough that does seem to be the case. For questions with fewer predictions they are more likely to have negative autocorrelation (mean-reverting) behaviour. The largest questions do seem to have at least some auto-correlation. (Eyeballing it, I would guess maybe ~.1 is a fair estimate?)
To make this concrete (and find out over what time horizon Metaculus is 'predictable'), I ran the same exercise, across 1-day, 2-day, etc autocorrelations, fitted a regression and took a point with a 'large' number of predictors. My adjusted autocorrelation chart looks as follows:
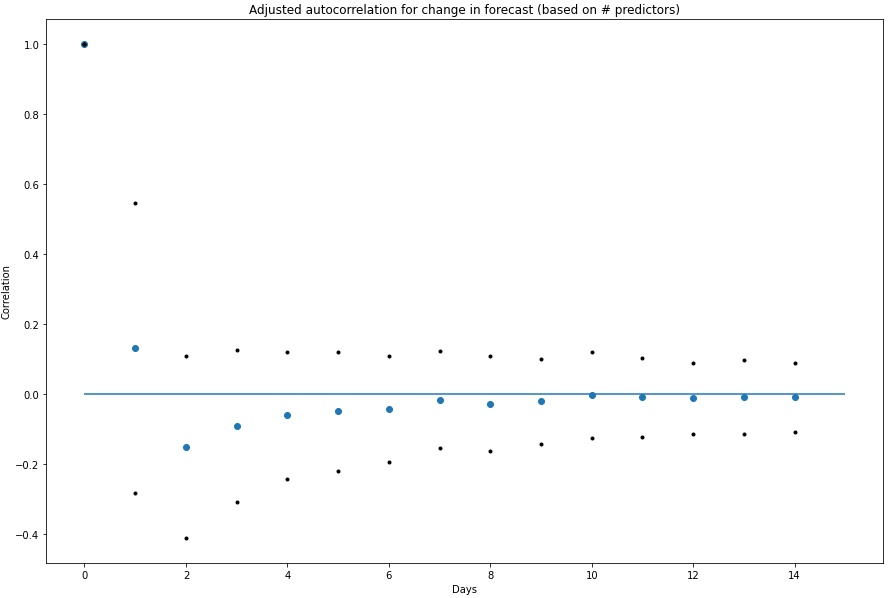
My takeaways from this are:
- Metaculus exhibits some slight momentum over a 1-day time horizon (although noise in the smaller questions dwarfs it)
- Over 2-days, this effect is nil, and in fact forecasts are slightly mean reverting
- My confidence that this applies to any specific question is pretty low
On the whole, I think this is pretty positive for Metaculus - I had to torture the data to show some very slight momentum, and even then I'm not completely convinced it exists.