EDIT: I tested this idea in a simulation and it (un)fortunately failed.

This post is an attempt to combine some parts of frequentism with some parts of Bayesianism. Unfortunately, there is a good deal of probability theory. I assume that "improper priors" are okay to use and that we have no prior knowledge about the population of which we are trying to learn.

THEORY

Let's say we're trying to estimate some parameter, B. If we interpret the likelihood function as a conditional probability function, we get a function for our posterior probability density function after taking n samples:

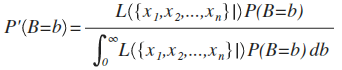
This yields an expected value of B:

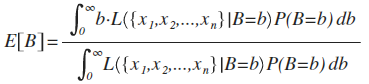
Now, intuitively, it would make a lot of sense if, given B=b, the expected value of our posterior probability density function turned out to be actually be B. In frequentist terms, it would be nice if our posterior distribution was unbiased:

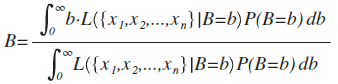
So, the question is: If we're trying to estimate a parameter of some distribution, can we pick a prior distribution such that this property is true?

EXAMPLE

Let's say that we have a uniform distribution from 0 to B. So, we draw a sample of "N" numbers with some maximum value "M". Now, let's examine the hypothesis that B=b, for some "b". If b<M, we know that B=b is impossible. If b>M, we know it is possible. In particular, the likelihood function becomes:

The expected value calculation turns out to be:

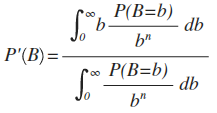
Now, I leave solving this equation as an exercise for the reader, but it turns out that if we let we get an unbiased estimator for B if

Now, of course, 1/x^2 is definitely not a proper prior distribution for the simple reason that its integral is infinite. However, if we use it as an improper prior distribution, then, any sample with maximum≠0 will yield a valid probability distribution.

DISCUSSION

As far as I know there is no law of probability that says our posterior probability function "should" have an expected value equal to the parameter. That being said it does seem like a positive trait for the function to have. I also suspect that this idea can be extended to a wide variety of distributions. That being said, we obviously tend to have  prior information in real life about our populations, so the practical effects of this idea are probably minimal.