Epistemological Status: I ran a basic simulation and this checks out. Specific details need refinement. Probably just a curiosity, but I think there's a chance there's a deeper connection here. I opted to post in the earlier stages incase I'm missing something big.

In biology, the quasispecies equation is used to model population structures of viruses. States are usually interpreted as genotypes for an individual. Commonly, these states represent proto-viral DNA/RNA strands. Transitions are mutations between these genotypes. Usually, the state genotype confers the replication rate and transitions are equivalent to mutations. The literal equation states that we can study the population dynamics with the mutation matrix $Q$ using, $π_{t + 1} = Q π_{t}$ Let's switch to the MDP setting. Assume the actions of the individual(s) have a deterministic effect on the environment transitions. We're going to interpret the rewards as a fitness score allowing the agent to continue propagating. First, let the transition matrix for the system be given as $T_{i j}$ . Second, transform each reward to the fitness $r_{i j} \to e^{\frac{1}{λ} r_{i j}}$ . The Quasispecies formala relates the population of individuals at each state after one stage of replication after we set $Q_{i j} = T_{i j} r_{i j}$ .

The individuals aren't intelligent. Instead, the fitness controls the replication rate of transitions. If $r = 0$ then the transition is neutral and the number of individuals collected on a state is neither amplified nor diminished. If $r ≪ 0$ then the transition is extremely harmful and if $r ≫ 0$ the transition is extremely helpful.

Notice that we can study the space of all possible transitions and conclude that, $π_{t} (s_{t}) = \sum s_{t - 1} Q_{s_{t - 1}, s_{t}} π_{t - 1} (s_{t - 1}) = \sum s_{t - 2} \sum s_{t - 1} Q_{s_{t - 1}, s_{t}} Q_{s_{t - 2}, s_{t - 1}} π_{t - 2} (s_{t - 2}) = \dots = \sum s_{0}, \dots, s_{t - 1} (Π_{k = 1}^{t} Q_{s_{k - 1}, s_{k}}) π_{0} (s_{0})$ To make further progress, remember that actions have deterministic effects so it's okay to assume individuals are fully random in their exploration. This allows us to simplify the product into, $Π_{k = 1}^{t} Q_{s_{k - 1}, s_{k}} = Π_{k = 1}^{t} T_{s_{k - 1}, s_{k}} {^r}_{s_{k - 1}, s_{k}} = t \prod k = 1 e^{\frac{1}{λ} r_{s_{k - 1}, s_{k}}} = e^{\frac{1}{λ} \sum_{k} r_{s_{k - 1}, s_{k}}}$ In words, we have decomposed the evolution of the population into a summation over all the paths an agent could take through the system. The twist, is that each path is weighted by an exponential term proportional to the reward that path receives from the environment.

Philosophically, this has the same spirit as the path integral approach used in physics. If we send $λ \to 0$ in the path integral, this is the thermodynamic limit, we'll get back the equations for classical motion. The claim is that the dynamics reinforce only the optimal paths in this limit.

Let's consider a toy-example. Say, there are only two paths. One provides $r_{1}$ return and the other $r_{2}$ . If $r_{1} > r_{2}$ then we have, $lim λ \to 0 λ log (e^{r_{1} / λ} + e^{r_{2} / λ}) = r_{1}$ It's not hard to see that this extends to any finite sum of paths. Say $π_{0} (s) = δ (s, s_{0})$ is an indicator function. $lim λ \to 0 λ log (π_{t} (s, λ)) = v (s, s_{0}, t)$ Where $v (s, s_{0}, t)$ is the optimal return for a $t$ -step path between $s_{0}$ and $s$ . Note, if the path doesn't exist this will be zero. Since we have no discounting, the return will generally become infinite. Luckily, this very situation is a strength of the quasispecies model. The long-term replication rate is given by the largest eigenvalue $α$ of $Q$ . In our formalism, $max s ρ (s) = lim λ \to 0 λ log (α (λ))$ This is equivalent to the long-term average reward of a population of agents distributed over the MDP. If we want the gain of a specific state then we study the quantity $Q^{t} π_{0} (s_{0})$ .

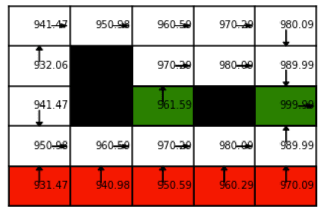
We can test these assumptions on a grid-world. Green and red states are terminal. Imagine a green state as a rewarding home-base. The left state gives unit reward and the right state gives ten units of reward. The red states act as a cliff that kills the agent. The agent is penalized by ten units of reward. All other states return zero reward in these states. The episode is terminated if the agent encounters either a green or red state. The value function for this MDP for $γ = 0.99$ is given as,

The max gain is returned as $\sim 10$ . If we multiply by the horizon of the discount rate ( $\frac{1}{1 - γ} \sim 100$ ) then we see that this formalism passes a first sanity check. The implication of all of this is that there's a bridge between replicon dynamics and true reinforcement learning.