The Bullwhip Effect

aysajan

Background

In the 1990s, when Procter & Gamble was examining the supply chain order patterns for one of its best-selling products, Pampers diapers, they discovered an interesting phenomenon. As they expected, the sales at its retail stores fluctuated moderately. However, as they moved further up in the supply chain, they observed greater and greater amplification in order variabilities at the distributor's and supplier's sites.

The supply chain phenomenon of this increasing variability of orders is called the Bullwhip Effect. It was named after the behavior of a whip when one swings from the origin (e.g., the increased amplitude of the whip in the figure below). The bullwhip effect is used to describe the amplifying demand variation in response to consumer demand as we move up in the supply chain. In this post, I will discuss when and why this effect happens and when and why it does not.

As an example, consider a simple shoes supply chain with a retailer, wholesaler, distributor, and manufacturer. Each week, supply chain members engage in a non-coordinated multi-step activities:

The retailer observes the customer shoes demand of the current week, satisfies the demand with the available inventory, and places an order with the wholesaler based on consumer demand forecasting for the next week.
The retailer’s order request causes the wholesaler to fulfill the order with the available inventory and then place a new order with the distributor by forecasting the retailer's order next week.
Moving further up in the supply chain, the distributor fulfills the order request from the wholesaler and places an order with the manufacturer by forecasting the wholesaler's order next week.
Finally, the manufacturer fulfills the wholesaler’s order request.

We are interested in analyzing order patterns of different participants over time when they face varying consumer demand. In particular, we are interested in evaluating the degree of demand/order variability in the supply chain as we move up the supply chain (i.e., move further away from the consumer). Let’s assume the manufacturer has unlimited capacity such that he/she is always able to fulfill any order request from the distributor. At each stage, if any participant (except manufacturer) lacks of inventory to satisfy demand of immediate downstream, he/she records a back-order, which needs to be fulfilled first from the next order. We express the relationship between the supply chain members using a simple chain:

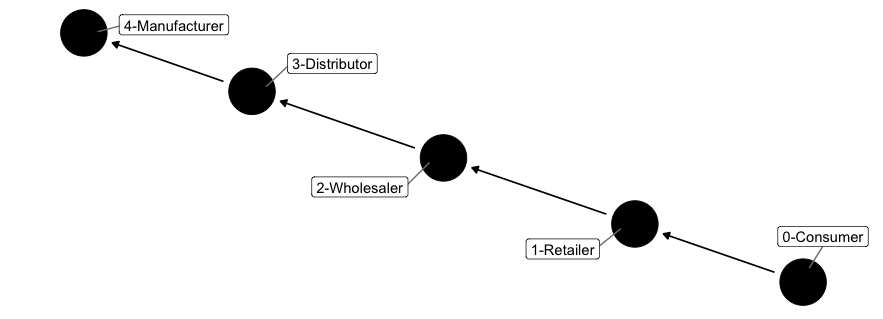
The Model

Let’s unpack demand/order patterns for each participant by defining explicit variables on demand/order, time, and supply chain levels. We first consider a case with no back order. The key steps are:

The retailer observes of consumer demand at week $t$ and satisfies the demand.
The retailer then places an order of $d^{1} (t)$ according to the forecast of consumer demand for week $t + 1$ .
The wholesaler receives the order request of $d^{1} (t)$ , fulfills it and places a new order $d^{2} (t)$ with the distributor.
Moving up the supply chain stream, the distributor fulfills the wholesaler’s order request of $d^{2} (t)$ and places an order of $d^{3} (t)$ with the manufacturer.
The manufacturer always fulfills the distributor’s order request.

Formally, $d^{n} (t)$ represents the demand/order quantity of the participant on level $n$ at week $t$ . For instance, $d^{1} (2)$ is the demand/order placed by the level 1 participant, i.e., the retailer, at week 2, $d^{3} (5)$ is the demand/order placed by the distributor at week 5, etc. To evaluate the degree of variation on demand/order, we need consumer demand $d^{0} (t)$ fluctuating over time, which serves as input. More generally, let's assume demand/order $d^{n + 1} (t)$ for the $(n + 1)^{th}$ upstream participant at time $t$ is a function of demands $d^{n} (t)$ , $d^{n} (t - 1)$ of the immediate downstream:

d^{n + 1} (t) = f (d^{n} (t), d^{n} (t - 1))

A change $ϵ^{n} (t)$ of demand $d^{n} (t)$ causes change in demand, thus order at the immediate upstream $n + 1$ :

\frac{\partial f}{\partial d^{n} (t)} = lim ϵ^{n} (t) \to 0 \frac{f (d^{n} (t) + ϵ^{n} (t), d^{n} (t - 1)) - f (d^{n} (t), d^{n} (t - 1))}{ϵ^{n} (t)}

⟹ f (d^{n} (t) + ϵ^{n} (t), d^{n} (t - 1))

\approx f (d^{n} (t), d^{n} (t - 1)) + \frac{\partial f}{\partial d^{n} (t)} \cdot ϵ^{n} (t)

\approx d^{n + 1} (t) + \frac{\partial f}{\partial d^{n} (t)} \cdot ϵ^{n} (t)

We can use the ratio $\frac{ϵ^{n + 1} (t)}{ϵ^{n} (t)}$ of demand variations to evaluate the impact of demand variability in the downstream on the demand in the immediate upstream:

\frac{ϵ^{n + 1} (t)}{ϵ^{n} (t)} = \frac{\partial f}{\partial d^{n} (t)}

What does this ratio look like in the context of different types of function $f$ ? We consider two general cases:

Case 1: Without back-order. For instance, supply chain members always have enough inventory to fulfill order requests from the downstream player, i.e., the orders are always fulfilled immediately without any lead time.

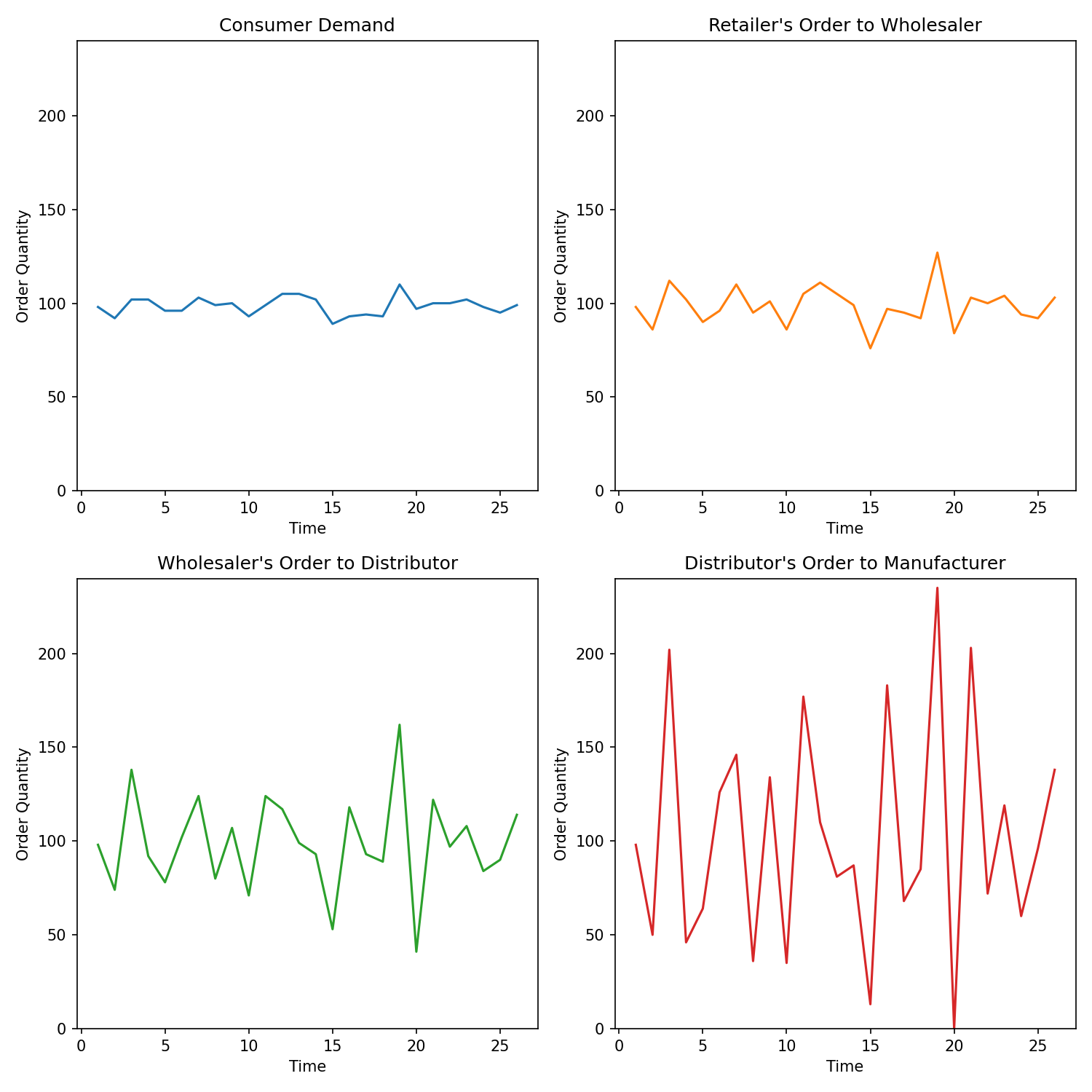
The amplification case. In this scenario we have $\frac{\partial f}{\partial d^{n} (t)} > 1$ . For instance,

f (d^{n} (t), d^{n} (t - 1)) = d^{n} (t) + [d^{n} (t) - d^{n} (t - 1)]

⟹ \frac{\partial f}{\partial d^{n} (t)} = 2

As a result, we can expect the demand variability of an upstream is always greater than those of the downstream members. In our shoes supply chain example, even when consumer demand do not seem to vary much, there is increased variability in the retailer's order to wholesaler, wholesaler's order to distributor, etc (see figure below, with consumer demand ~ $N (100, 5)$ ).

Increasing variability of orders up in the shoe supply chain

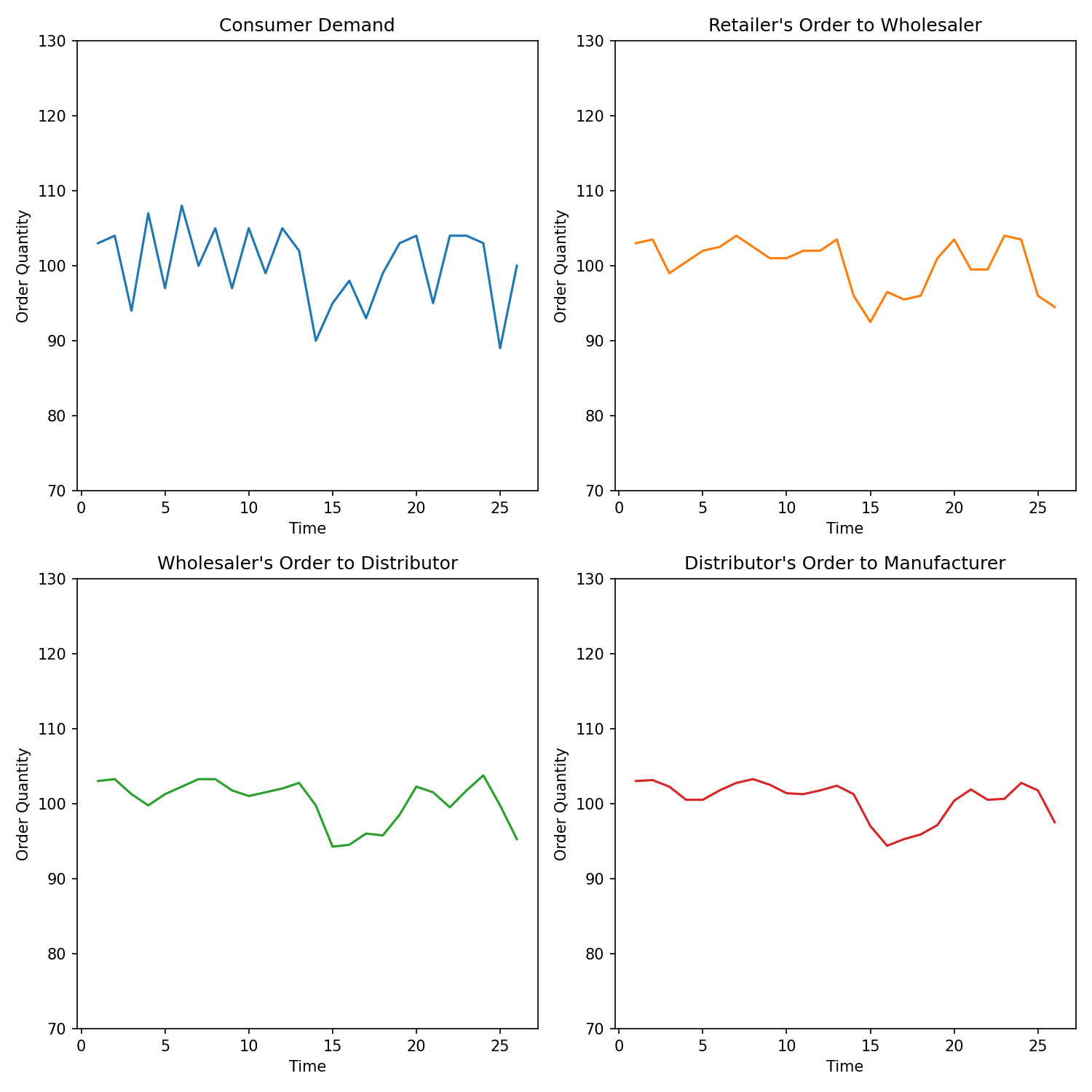
The damping case. This scenario is associated with $\frac{\partial f}{\partial d^{n} (t)} < 1$ . For instance, consider a two-step moving average function:

f (d^{n} (t), d^{n} (t - 1)) = \frac{d^{n} (t) + d^{n} (t - 1)}{2}

⟹ \frac{\partial f}{\partial d^{n} (t)} = \frac{1}{2}

Thus, we have a decreasing demand variability of the upstream players. In our shoes supply chain, compared to the consumer demand variability, we observe decreased variability in the retailer's order to wholesaler, wholesaler's order to distributor, etc (see figure below, with consumer demand ~ $N (100, 5)$ ).

Decreasing variability of orders up in the shoe supply chain

The no-change case with $\frac{\partial f}{\partial d^{n} (t)} = 1$ . Let's consider naive forecasting model where a member orders exactly the same as the demand from the immediate downstream:

f (d^{n} (t), d^{n} (t - 1)) = d^{n} (t)

⟹ \frac{\partial f}{\partial d^{n} (t)} = 1

As a result, there is no change in demand variability up in the supply chain.

Case 2: With back-order. In this instance, each player starts with an initial inventory and fulfill orders depending on the available inventory. If there is no inventory left, it will be back-ordered and fulfilled first from the order placed next period.

Formally, demand/order $d^{n + 1} (t)$ for the $(n + 1)^{th}$ upstream player is a function of demand $d^{n} (t)$ of the immediate downstream and its own available inventory $v^{n + 1} (t)$ at time $t$ :

d^{n + 1} (t) = f (d^{n} (t), v^{n + 1} (t))

A change $ϵ^{n} (t)$ of demand $d^{n} (t)$ causes change in demand/order at the immediate upstream:

\frac{\partial f}{\partial d^{n} (t)} = lim ϵ^{n} (t) \to 0 \frac{f (d^{n} (t) + ϵ^{n} (t), v^{n + 1} (t)) - f (d^{n} (t), v^{n + 1} (t))}{ϵ^{n} (t)}

⟹ f (d^{n} (t) + ϵ^{n} (t), v^{n + 1} (t))

\approx f (d^{n} (t), v^{n + 1} (t)) + \frac{\partial f}{\partial d^{n} (t)} \cdot ϵ^{n} (t)

\approx d^{n + 1} (t) + \frac{\partial f}{\partial d^{n} (t)} \cdot ϵ^{n} (t)

Similarly, we can use the ratio $\frac{ϵ^{n + 1} (t)}{ϵ^{n} (t)}$ to evaluate the impact of demand variability in the downstream on the demand in the immediate upstream:

\frac{ϵ^{n + 1} (t)}{ϵ^{n} (t)} = \frac{\partial f}{\partial d^{n} (t)}

What does this ratio look like in the context of a specific function $f$ ? We consider a simple case:

f = d^{n} (t) + [d^{n} (t) - v^{n + 1} (t)]^{+}, where

[d^{n} (t) - v^{n + 1} (t)]^{+} = {\begin{matrix} d^{n} (t) - v^{n + 1} (t), & if d^{n} (t) > v^{n + 1} (t) 0, & if d^{n} (t) \leq v^{n + 1} (t) \end{matrix}

The first instance is associated with back-order and second one with no back-order. As a result, we have

\frac{\partial f}{\partial d^{n} (t)} = {\begin{matrix} 2, & if back-order 1, & if no back-order \end{matrix}

Therefore, we have a non-decreasing demand variability up in the supply chain.

Summary

The bullwhip effect in supply chain illustrates that even when the consumer demand does not vary much, there is an increased variability up in the supply chain. This post suggests that bullwhip effect is not always present in a supply chain and the degree of variability heavily depends on the demand forecasting model used by the supply chain participants. For instance, when a two-step moving average is used, the degree of variability decreases; when an exponential-smoothing model with a smoothing factor of 1 is used, the degree of variability amplifies, causing inefficiencies in inventory management, capacity planning, etc. From the perspective of each member in the supply chain, the member should share the demand data with the upstream participants so that they all have access to the same raw demand data to update their forecast.

Source code is available at https://github.com/AysajanE/bullwhip_with_dag.

[-]Gunnar_Zarncke3y80

There is a game that is used to teach students of supply chain logistics this intuitively. I have always wanted to try this out in an LW meetup: https://en.wikipedia.org/wiki/Beer_distribution_game

[-]aysajan3y10

Yes. The beer game has been frequently used in undergraduate and MBA programs when professors introduce the bullwhip effect.

[-]Ericf3y10

That game doesn't work if any participant has heard of it, or the effect, just FYI

[-]Gunnar_Zarncke3y40

Do you predict this or know from first-hand experience?

It's just a prediction, based on the first time I read about that "game" and thought about what I would do in it.

[-]Gunnar_Zarncke3y30

Most people are not like you. Try it out like this:

https://twitter.com/ESYudkowsky/status/1414647916728229912

[-]Ericf3y30

But "people who are taking a training where that game would be used" are much closer.

And note that I didn't say I saw the solution when presented with the game rules alone - only when I had finished reading through to the conclusion, and then thought about it. Which is a much lower bar.

[-]aysajan3y30

I disagree. The key factor to observe bullwhip effect is no coordination among players. For example, retailer does not share consumer demand information with the wholesaler, and the wholesaler does not share demand information with the distributor, etc.

If anyone knows about the simulation, and they play to win, they will implement a dampening effect at whatever stage they are (assuming they don't just say something out loud before things start, and let everyone do it). Depending on the exact mechanics of the game, there are different ways to smooth out demand fluctuations at minimal cost.

[-][anonymous]3y10

(e.g., the increased wavelength of the whip in the figure below)

Don't you mean increased amplitude?

Yes, "amplitude" is a more appropriate word. I've changed it. Thank you.