Here are some updates on the work that @Jeremy Gillen and I have been doing on Natural Latents, following on from Jeremy's comment on Resampling Conserves Redundancy (Approximately). We are still trying to prove that a stochastic natural latent implies the existence of a deterministic latent which is almost as good.

First, if a latent is a deterministic function of X and Y, (ie. $\Lambda =f(X,Y)$), the deterministic redundancy conditions will be satisfied up to errors of $H\left(Y|X\right)$ and H(X|Y). (We don't actually use this in anything that follows, but think its quite nice.)

Furthermore, we can always consider a latent which just copies one of the variables (for example $\Lambda =Y$). This kind of latent will always perfectly satisfy one of the deterministic redundancy conditions (if $\Lambda =Y$, then $H\left(\Lambda |Y\right)=0$ ). The other deterministic redundancy condition will be satisfied with error $H\left(\Lambda |X\right)=H\left(Y|X\right)$. The mediation condition will also have zero error since $I(X;Y|\Lambda )=H\left(Y|\Lambda \right)-H(Y|X,\Lambda )=0$ (since $H\left(Y|\Lambda \right)=0$).

We can choose $\Lambda$ to copy either $X$ or $Y$, meaning that using this method we can always construct a deterministic natural latent with $\text{error}=\text{min}\left[H\right(Y|X),H(X|Y\left)\right].$

Another deterministic latent that can always be constructed is the constant latent $\Lambda =const.$ This will always perfectly satisfy the two deterministic redundancy conditions, since $H\left(\Lambda |X\right)\le H\left(\Lambda \right)=0$. The mediation error for the constant latent is just the mutual information between $X$ and $Y$.

Between these two types of latent, a deterministic natural latent can always be constructed with error bounded by $\text{min}\left[I\right(X;Y),H(X|Y),H(Y|X\left)\right]$. Loosely: if $X$ and $Y$ are highly correlated you can use the copy latent and if $X$ and $Y$ are close to being independent, you can use the constant latent.

To test how tight this bound is, Jeremy has numerically found the optimal deterministic and stochastic natural latents for a family of (X,Y) distributions. The distribution is parametrised by $\alpha$ which captures how correlated $X$ and $Y$ are ($\alpha =0$ implies perfect correlation and $\alpha =1$ implies no correlation). A nice graph of these results is below:

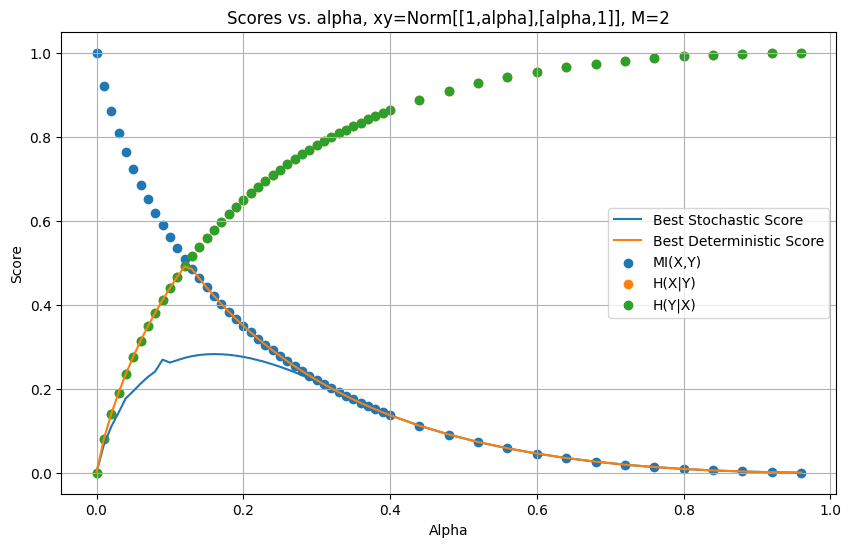
The ‘score’ of the latents is the sum of the errors on the mediation and redundancy conditions. The fact that the best deterministic score closely hugs the line $min\left[I\right(X,Y),H(Y|X\left)\right]$ suggests that the bound we found above is pretty tight. When we look at the latents found by the numerical optimizer, we find that it is using the copy latent at low $H\left(Y|X\right)$ and the constant latent when$I(X;Y)<H\left(Y|X\right)$.

We also have a graph which breaks down the individual errors for optimal stochastic and deterministic latents:

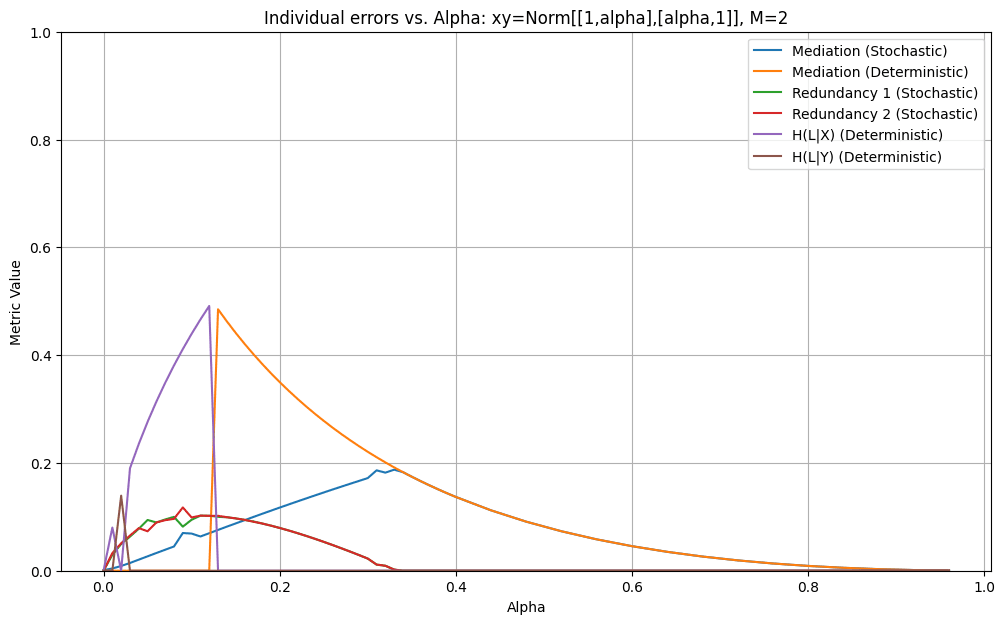
It shows quite clearly the point where the optimal deterministic latent switches from ‘copy’ to constant around $\alpha =0.1$. Furthermore, for $\alpha >1/3$ we have shown that the constant latent is at a local minimum in the space of possible stochastic latents. We did this by differentiating with respect to the conditional probabilities $P(\Lambda |X,Y)$ and finding the Hessian. This was done using a symbolic program so we don’t have a compact proof to put here. The point $\alpha =1/3$ is also the point where the errors for the best stochastic and deterministic latents become the same. This seems like good news for the general NxN conjecture, since it shows that when two states are roughly independent, there’s zero cost (to the difference between stochastic and deterministic scores) to ‘merging’ those states from the perspective of the latent.

Eyeballing the first graph, it seems like the deterministic score is never more than twice the best stochastic score for any given distribution. It is interesting to note that the optimal stochastic latent roughly follows the same pattern as the deterministic latent but it notably performs better than the deterministic latent in situations where both $H\left(Y|X\right)$ and $I(X;Y)$ are high. Bear in mind that these graphs are just for one family of distributions (but we have tested others and got similar results). 

At the moment we are thinking about ways to lower bound the stochastic latent error in terms of $I(X;Y)$ and $H\left(Y|X\right)$. For example if we could show that it is impossible for a stochastic latent to have a total error less than $\frac{1}{n}\text{min}\left[I\right(X;Y),H(Y|X),H(X|Y\left)\right]$ then this would prove that the existence of a stochastic latent with error $ϵ$ implies the existence of a deterministic latent with error $nϵ$ or less. We are also thinking about ways to show that certain latent types have errors which are global minima (as opposed to just local minima) in the space of possible latents.