Disambiguation: What I’m talking about here is essentially the same thing that John Wentworth works on and writes about, including in Public Static: What is Abstraction?, and I stole some of the things he’s written (by quoting him directly) to save myself time. But I think this post has a different aim from anything I’ve read from him or anyone else (which isn’t to say no one has written a post with this aim; someone probably has). 

For a very quick TL;DR, I'd suggest reading the Definitions section and the Abstract Answer subsection.

Aim

My aim is to get readers (with approximately any background?) to understand the concept of abstraction; see that the concept is ubiquitous in the world and even in their lives; appreciate the usefulness of the concept; hone the skill of recognizing, generating, and utilizing abstractions; internalize the concept deeply enough to install the habit of employing this skill in the wild; and, ideally, learn to love the concept.

Simply skimming this post will hopefully partially serve all of these purposes, but I think doing the exercises included below is probably also an important component.

I expect this to be less valuable if you are already familiar with the concept of abstraction, but perhaps skimming this post will still lead you to encounter some valuable new perspectives on it.

Definitions

Abstraction is a conceptual process in which general rules and concepts are derived from specific examples by identifying shared high-level features and ignoring low-level differences. ‘An abstraction’ is the outcome of this process: a general idea that unifies a collection of specific objects, especially in a way that provides non-trivial insight into the nature or relationships of those objects.^[1]

John Wentworth said:

Anyway, (my reading of) Jaynes' answer to the main question: abstraction is mainly about throwing away or ignoring information, in such a way that we can still make strong predictions about some aspects of the underlying concrete system.

These are closely related definitions of abstraction; having multiple framings available to you may be helpful.

Introductory Examples

This section contains a bunch of examples of abstractions - I urge you to read as many as you need to feel like you have a handle on the basic concept, then skip to the next section. That's because in this section, for the sake of simplicity and clarity, the abstractions are fairly mundane; I don't expect many people to find them very exciting. Later in this post, I'll try to provide more exciting examples, and provide exercises that allow you to generate exciting examples for yourself.

Circle

• Definition: A 2-D closed figure such that every point in the figure is the same distance from some central point
• This is an abstraction because lots of specific objects fit the definition of a circle. All the figures in the following image are circles, but they are all different:

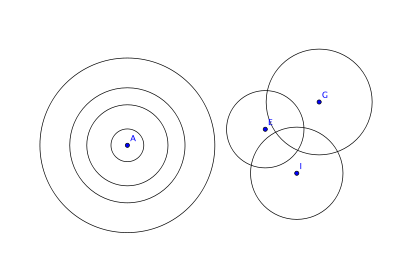
• We often use the word “circle” to refer to things that are only approximately circles: ovals, frisbees, plates, people sitting in a circle, etc. We sometimes utilize the fact that their shapes share some properties with circles. For example, one reason people might choose to sit in a circle is to ensure that everyone receives heat from a fire at the center, and this shape is effective for that purpose because everyone is equidistant from the center.
• There are useful things we know to be true about circles in general. For example:
  • Circle theorems
  • General principles for circular motion and rotation in physics
• Basically any 2D shape (square, rectangle, parallelogram, etc.) is an abstraction.

Metaphor

• The concept of "metaphor" is an abstraction because it unifies all examples of metaphors. What they have in common is that they are all comparisons between things that aren't directly related, but the things being compared and the nature of the comparison are different for each metaphor.
• Examples: You probably already feel familiar enough with metaphors to not need examples, and it's easy to look up examples of simple metaphors online. Two examples of more sophisticated metaphors, which are important enough for their books to be named after them, are The Lord of the Flies and The Catcher in the Rye. For a sophisticated example that you can read in about one minute, see Stopping by Woods on a Snowy Evening, by Robert Frost.
• As a reader, knowing the general concept of metaphors allows you to notice more of them and not have them go over your head. As a writer, knowing the concept of metaphors allows you to use metaphors to communicate ideas with more sophistication and subtlety (among other things).
• Basically any rhetorical device is an abstraction.

The Quadratic Formula

• Firstly, expressing a generic quadratic equation as ax${}^2$ + bx + c = 0 is an abstraction which unifies all quadratic equations, since they can all be expressed in this form for some specific values of a, b, and c. The quadratic formula builds on top of this abstraction.
• Every quadratic equation has a pair of solutions^[2], and the quadratic formula is an abstraction because it unifies the pairs of solutions associated with all quadratic equations. The pair of solutions to any given quadratic equation is an example of this abstraction. For instance, the fact that x = 1 and x = -1 are the solutions to x${}^2$ - 1 = 0 is an example of this abstraction.^[3]
• Knowing the quadratic formula allows you to solve quadratic equations in many contexts where doing so is useful. There are many such pure math contexts, but also more directly practical ones, like figuring out where a projectile will land when it is launched at a given angle and initial velocity.
• Lots of math rules are abstractions:
  • Exponent rules
  • Log rules
  • Sum rules
  • Differentiation rules
  • Integration rules

Examples from John Wentworth's Public Static: What is Abstraction?:

• We have a gas consisting of some huge number of particles. We throw away information about the particles themselves, instead keeping just a few summary statistics: average energy, number of particles, etc. We can then make highly precise predictions about things like e.g. pressure just based on the reduced information we've kept, without having to think about each individual particle. That reduced information is the "abstract layer" - the gas and its properties.
• We have a bunch of transistors and wires on a chip. We arrange them to perform some logical operation, like maybe a NAND gate. Then, we throw away information about the underlying details, and just treat it as an abstract logical NAND gate. Using just the abstract layer, we can make predictions about what outputs will result from what inputs. Note that there’s some fuzziness - 0.01 V and 0.02 V are both treated as logical zero, and in rare cases there will be enough noise in the wires to get an incorrect output.
• I tell my friend that I'm going to play tennis. I have ignored a huge amount of information about the details of the activity - where, when, what racket, what ball, with whom, all the distributions of every microscopic particle involved - yet my friend can still make some reliable predictions based on the abstract information I've provided.
• When we abstract formulas like "1+1=2*1" and "2+2=2*2" into "n+n=2*n", we're obviously throwing out information about the value of n, while still making whatever predictions we can given the information we kept. This is what abstraction is all about in math and programming: throw out as much information as you can, while still maintaining the core "prediction" - i.e. the theorem or algorithm.
• I have a street map of New York City. The map throws out lots of info about the physical streets: street width, potholes, power lines and water mains, building facades, signs and stoplights, etc. But for many questions about distance or reachability on the physical city streets, I can translate the question into a query on the map. My query on the map will return reliable predictions about the physical streets, even though the map has thrown out lots of info.^[4]

The Significance of Abstraction

Why is abstraction a useful concept? What exactly does it allow us to accomplish?

Abstract Answer

Given an abstraction, there are two main uses (that I know of): incorporation and generation of new examples into the framework defined by the abstraction.

• Incorporation:
  • Once you have an abstraction, and know the commonalities that all examples of that abstraction share, you can often recognize, understand, reason about, solve, or work with new examples that you are faced with much more effectively than you would have been able to if you were not familiar with the abstraction to which it belonged. The more insight the abstraction provides into the nature and relationships of its instances, the more useful it is.
• Generation: 
  • In many cases, knowing an abstraction which highlights common features of many objects makes it easier to produce new instances of that abstraction.

Concrete Answer

Abstraction in action shapes the world, and will likely do so even more radically in the future. Multilayered abstractions are critically useful, and it intuitively seems to me that the extent to which we can use them is the main difference between humans and other animals that allows us to shape the world to our desires as much as we do.^[5] Everyone relies on tools that other people provide without having the first clue how to produce them themselves (e.g. houses, cars, electronic devices, the internet, software packages, etc.), but because using these tools only requires knowledge of how to directly interface with them rather than low-level details of how to create them, we can build on each other’s work very effectively. Further, the creation of many of these tools also utilizes other deeper abstractions, which themselves are often built on abstractions, and so on for many levels. The state of human civilization today is the result of millennia of progress, much of which can be attributed to the development and application of new abstractions. This progress may have brought us to The Precipice, and the way we build on the abstractions we currently have in the near future may have a dramatic influence on the long-term future.

The Value of Being Consciously Aware of Abstraction

Frankly, abstraction may not be the most important idea to be consciously aware of, since people use it by default without paying too much direct attention to it. For example, here are a couple of abstraction exercises that I tried to do:

1. Look for areas where abstractions are clearly useful to other people for things you care about, and familiarize yourself with those abstractions, or find ways to use them more effectively if you already are familiar with them.
2. Figure out places where abstractions (or insights related to abstractions) would be useful for things you care about but haven’t yet been developed, and try to produce them.

If these exercises generate useful ideas for you, that's great! But they didn't for me. While at first I expected these to lead to useful insights, I realized after a few minutes that most of the things that came to mind were already familiar, and I just hadn't explicitly thought about them from the lens of abstraction before. They included things along the lines of "Read more about AI alignment (to figure out what relevant abstractions I'm not aware of yet)," "Get good at ML engineering," "Study more math," "Try to generate meaningful theoretical results for AI alignment", etc. The answers didn't really feel very abstraction-related, because that wasn't the most natural language in which to express them.

After that, my view on the value of being consciously aware of the concept of abstraction changed. I still do think that being deeply familiar with the concept of abstraction (in the ways described in the Aim section above) can help a lot. However, this value doesn't come from just thinking about abstraction and getting a major shortcut to large important ideas. Instead, it makes you less likely to miss opportunities to learn general lessons. It makes you more likely to notice when cool things you come across share properties with other interesting things you've previously seen, and that kicks off a mental process that allows you to synthesize generalizable takeaways.

Getting Excited about Abstraction

By this point, I have on numerous occasions come across something, realized it is an example of an abstraction, and thought "Woah, that's super cool! I totally feel like I've seen this general idea in a bunch of interesting places." Then, I have often had one or more of the following thoughts:

• "Where have I seen examples of this?" (Retroactive recognition)
• "Can I come up with original examples of this?" (Generation)
• "How can I make use of this?" (Planned future incorporation or generation)

I would then try to answer those questions, and a reasonable proportion of the time I had enough success to find it fruitful. Each time, this activity made a new abstraction more familiar to me, and I became more likely to incorporate new examples of it that I came across into an existing framework in my mind.

In the hopes that I can recreate this experience for you, this section will consist of:

1.  Examples of abstractions that I find exciting, and 
2.  Exercises for you to actively engage with abstraction.

If you are comfortable sharing, please put your responses to any or all of the exercises in the comments!

Unique Example: Abstraction Itself

The notion of abstraction is itself an extraordinarily deep and powerful abstraction. This whole post is dedicated to analyzing it through its examples and uses! It is the one that I most want you to appreciate, but I think you come to appreciate it by getting excited about several other examples of abstraction, and then registering that the thing that all of those have in common is that they are abstractions.

This may take some time, since the process is highly recursive: to appreciate the notion of abstraction, you first need to appreciate many abstractions, but to appreciate abstractions, you need to appreciate their specific examples, and sometimes those are also abstractions, and so on.^[6] The good news is that I think this process gives rise to deeply intellectually satisfying and enlightening trains of thought, and is extremely fun. The next few subsections are all aimed at walking you through this process, so let's get into it!

One quick note before we do: Keep in mind that different prompts and examples will resonate for different people. It's fine if some of them don't work for you - hopefully, at least some of them will.

Things with Precise Definitions

Many things that have precise definitions are abstractions. The circle example above fits this category.

Exercise: 

Make a list of abstractions that have precise definitions. Write down some examples and some of the key insights that these abstractions provide or allow for (e.g. theorems related to them). Continue until you feel like you have a good grasp on the richness of this class of abstractions (or until you think it's unlikely that will be attainable in a reasonable amount of time).

Suggested starting point: Look at the high-level topics, core results, and major theorems covered in STEM subjects you have previously studied (ideally ones where you know the material particularly well), and try to identify abstractions within them. You may want to look at syllabi, review guides, cheat sheets, etc. which give concise overviews of important high-level topics. (I think this is probably easiest for math and theoretical computer science courses.)

• It's fine if you don't systematically analyze every abstraction - do some of it quickly in your head, and only spend more time on and write down the abstractions, examples, and insights you find particularly interesting.
• Look for, and keep track of, multilayered abstractions.

My Examples:

This is essentially my (relatively brief) response to the exercise above. Looking at some of my examples may help you come up with ideas, but it may also use up some of the things you could have come up with on your own. I don't go into detailed descriptions of these abstractions or insights, and I only thought of examples in my head rather than writing them down, so this may not be very legible if you aren't already familiar with the subjects I draw from. My list may be unsatisfying to you, but your list should not be, since it should contain abstractions and insights that you are familiar with.

Indented bullets indicate nested abstractions; if an object is an example of the sub-bullet, that implies it is also an example of the parent bullet. ^[7]

Computer Science Theory

Abstractions

• Languages
  • Recognizable languages
    • Decidable languages
      • Context-free languages
        • Regular languages
          • Finite languages
  • Undecidable languages
    • Non-trivial properties of recognizable languages

Insights

The layers of abstraction indicated above encode several key results themselves.

• Finite$⟹$Regular$⟹$Context-free$⟹$Decidable$⟹$Recognizable
• There are interesting problems which cannot be solved by any algorithm.
  • Rice's Theorem: All non-trivial properties of recognizable languages are undecidable.
  • There are more unrecognizable languages than recognizable ones. (Both classes are infinite, but there are uncountably many unrecognizable languages and only countably many recognizable ones.)

Abstract Algebra

Abstractions

• Sets
  • Groups
    • Rings
      • Fields
• Functions
  • Homomorphisms
    • Isomorphisms
      • Automorphisms

Insights

• Lagrange's Theorem
• Cayley's Theorem
• Sylow Theorems
• Classification of finite simple groups (though we didn't quite get through the full proof of this one in my class)
• Fundamental Theorem of Galois Theory
• Insolubility in radicals of general polynomial equations of degree 5 and higher

There are a lot of other abstractions and theorems here - it's called abstract algebra for a reason!

Game Theory

Abstractions

• Strategy spaces
• Payoff functions
• Games
  • Stage games
  • Repeated games
  • Bayesian games
    • Mechanisms
      • Auctions
        • Standard auctions
      • Direct mechanisms
• Nash equilibria
• Shapley values

Insights

• General approaches for determining reasonable or expected behavior in multi-agent settings. Standard settings include:
  • Setting prices in competitive markets
  • Selecting production quantities in competitive markets
  • Deciding whether a firm should enter / exit a competitive market
  • Bidding for an object when you value it a certain amount, in various types of auctions
• Nash's Theorem
• Folk Theorem
• Revenue Equivalence Theorem
• Revelation Principle

Problem Solving Techniques

There are many problem solving techniques that are effective for large classes of problems. For example, doing a sanity check when you arrive at a solution to a problem often helps catch major flaws.

Exercise: 

Make a list of problem solving technique abstractions. Write down some examples and some of the key insights that these abstractions provide or allow for. Continue until you feel like you have a good grasp on the richness of this class of abstractions (or until you think it's unlikely that will be attainable in a reasonable amount of time).

• It's fine if you don't systematically analyze every abstraction - do some of it quickly in your head, and only spend more time on and write down the abstractions, examples, and insights you find particularly interesting.

Prompts: 

• Think about places where you’ve seen step-by-step instructions. Can you follow those instructions to accomplish more than one task?
• Imagine you are faced with a generic problem. What do you do to try and solve it?
• How have you actually addressed concrete problems you’ve faced in the (recent) past?
  • Math problems
  • Difficult decisions
  • Long-term life goals

My Examples:

• All the math rules listed with the quadratic formula example above
• All the instrumental rationality techniques in the Hammertime sequence (the intro post describes why these are abstractions). I particularly like Yoda Timers and Murphyjitsu.
  • Some problems I've solved and things I've done with Yoda Timers:
    • Reached out to people to set up meetings and activities
    • Found a way to remove a common distraction (by removing the shortcut to the videos page on Facebook)
    • Made decisions about whether or not to buy things
    • Bought things
• When making a decision, make a conscious effort to be an expected utility maximizer. Consider your space of possible options. Assign probabilities to different outcomes conditional on you selecting each of those options. Decide how good you think each possible outcome would be, all-things-considered (i.e. the utility of each outcome). Select the option with the highest expected value. (I find this very useful in practice sometimes, despite the practical difficulties that arise.)
• It is sometimes helpful to approach difficult questions by thinking about the properties that their answers must have.
  • In an earlier draft of this post I went into great detail about this example - I don't think that's necessary to include, and I never finished revising that section, but if you want to see it, it's in this Google doc. The examples use cases I discuss there are:
    • Trying to decide what materials to put in the syllabus for a reading group
    • Doing mathematical induction proofs
    • Deriving the form of the time evolution operator in quantum mechanics
    • Answering the question, "Why is there something rather than nothing?" (Don't get too excited - I no longer think it's a completely convincing resolution, as my comment in the doc suggests. Even if it were, it would only be somewhat satisfying.)
• "Have you tried turning it off and on again?" Because that often solves electronic glitches.
• Asking for help
• Taking a step back when stuck, and looking at the problem as a whole
• For problems where it is difficult to see a principled next step to take, using a brute force approach is often useful. Seeing the particular ways in which naïve solution attempts fail can highlight properties that the actual solution must have, and that you can use to direct your search to more promising subsets of all possible solutions.
• If you are trying to show that something is true in general, and don't have a clear sense of how to do it, look at some specific cases in which it's true and try to figure out why it's true. If it is in fact true in general, then the general reason it is true is manifesting itself somehow in each specific example, and seeing how it manifests itself can help discover the general reason.

Storytelling Abstractions

There are countless themes, ideas, principles, strengths, and shortcomings that are shared across stories of all kinds. Numerous stories are variants of the Hero's Journey: "the common template of stories that involve a hero who goes on an adventure, is victorious in a decisive crisis, and comes home changed or transformed." Many stories suffer from deus ex machina, in which "a seemingly unsolvable problem in a story is suddenly and abruptly resolved by an unexpected and unlikely occurrence" (though sometimes this can be intentional and serve a purpose).

Exercise: 

Come up with as many storytelling abstractions as you can. Also, come up with as many examples of each storytelling abstraction as you can.

Prompts: 

• To first familiarize yourself with some storytelling abstractions, explore the tvtropes website. Be warned: If you are anything like me, this site may well lead you down very fun but time-consuming rabbit holes. If you want to avoid this, consider skipping this prompt or setting a timer to limit your exploration. You may want to use the Random Trope button, or go to the tvtropes page of some book, movie, TV show, TV episode, or story in any other medium that you have enjoyed. (For the latter, use the search bar, and select the page that has the medium in parentheses next to the title, e.g. “Breaking Bad (Series)”. Some things I’ve searched for didn’t have pages, but most did.) For tropes (i.e. abstractions) that resonate with you, try to think of other stories that have examples of them. Bonus: try to come up with your own original ideas for scenes or stories that fit the trope!
• Pick a story that you have greatly enjoyed. Spend some time trying to identify what aspects of the story you enjoyed. For each, abstract away the details and identify what general thing this aspect of the story did which you liked. Try to think of other stories that also did that thing.
  • For stories you haven’t completed recently, it may only be possible to extract very high-level abstractions. You could look up summaries of the stories, or reread / rewatch / relisten to them, to identify lower-level abstractions. You could also make this an ongoing exercise in which every time you love a story from now on, you revisit this prompt.

My Examples:

• Almost all great character moments involve people experiencing certain feelings and demonstrating how they act when they experience those feelings. The best stories have settings and plots that brilliantly take their characters on beautiful and terrible journeys through intense, relatable, and striking feelings and actions. Example feelings: anger, jealousy, love, hatred, respect, joy, fear, insecurity, sorrow, disgust, surprise, awe, determination / agency, resignation, excitement, nervousness, relief, satisfaction, shame, embarrassment, pride, guilt, amusement, gratitude, disappointment, loneliness, boredom, patience, indignation, empowerment, uselessness, confusion, responsibility, apathy, vengefulness, exhaustion, doubtfulness, bitterness, shock, nostalgia.
  • Stories that contain examples of this:^[8]
    • The Kingkiller Chronicle
    • The Stormlight Archive
    • Spinning Silver
    • Song of Solomon
    • The Dark Knight
    • Pulp Fiction
    • Inception
    • Forrest Gump
    • The Prestige
    • It’s a Wonderful Life
    • The Wire
    • Breaking Bad
    • Attack on Titan
    • The West Wing
    • The Office
    • Extraordinary Attorney Woo
    • Arcane
  • Generative power: I've never actually seriously written a story, but I've wanted to write a book for a very long time and kept track of book ideas I've had. Using this abstraction as a prompt has led to some very fruitful idea generation.
    • "How can I develop a setting and core plot structure that do an amazing job of putting characters in as many contexts that induce rich feelings and meaningful actions as possible?"
    • Given a character that I already have some ideas for, "What interesting situations might make this character experience X? What actions might this character take in those situations?" Where X is some feeling from the list above. The reason I included so many feelings in that list is that having them readily available makes it much easier to use these questions as an algorithm for generating good ideas.
• Many excellent scenes or story arcs are based on character decisions, where we know exactly what the options available to the character are, and the story carefully explores the (emotionally weighty) pros and cons of the options. 
  • Examples (which hopefully make sense to people who are familiar without being spoilers^[9]):
    • Midnight Sun^[10] (Season 3, Episode 18 of Attack on Titan)
      • Levi, Erwin, and Armin
    • Two Cathedrals^[10] (Season 2 finale of The West Wing)
      • Bartlett, running for president
    • At least two in The Stormlight Archive: 
      • Near the end of Words of Radiance (book 2)
        • Kaladin, Elhokar
      • Near the end of Oathbringer (book 3)
        • Dalinar, Odium
  • Generative power:
    • Given a character that I already have some ideas for, "What does this character value? How would they make tradeoffs between the things they value? What interesting situations can I put them in that force them to make difficult tradeoffs?"
• Perfect imperfection can be at least as good as regular perfection. By perfect imperfection, I'm referring to scenes where some things clearly go wrong, but the outcome is still beautiful.
  • Examples (which hopefully make sense to people who are familiar without being spoilers^[9]):
    • One wedding in each of The Office, Parks and Recreation, and Brooklyn 99
    • One of the Eolian scenes in The Name of the Wind
• Having answers to the question "Why?" as often as possible tends to make stories better. Relatively few things should go unexplained or have to be taken on faith.
• Story components should be as interconnected as possible. If you make a graph with characters, settings, and plot events as nodes, then add edges between pairs of nodes that are related in some (meaningful) way, it is good for this to be as close to a complete graph (a graph in which each node is connected to every other node) as possible.
  • Spinning Silver is one of the best examples of this I know
  • Deus ex machina is an extreme violation of this principle 
• Sanderson's Three Laws of Magic Systems^[11]
  • Sanderson's First Law. “The author's ability to resolve conflicts in a satisfying way with magic is directly proportional to how well the reader understands said magic.”
  • Sanderson's Second Law. “Limitations are more interesting than powers.”
  • Sanderson's Third Law. “Expand what you already have before you add something new.”
• Some tropes from tvtropes I like:
  • Awesome Music
  • Chekhov's Gun
  • Moment of Awesome
  • Debt Detester
  • Grey and Gray Morality
  • Wham Episode and Wham Line

Concluding Exercises:

1. Tell me important things I've gotten wrong about abstraction, or important things I failed to mention, in the comments.
2. Lots of abstractions belong to the classes of "things with precise definitions," "problem solving techniques," and "storytelling abstractions." Come up with three other large classes of abstractions.

Miscellaneous

1. It seems to me that much of the field of mathematics is a large stack of abstractions. Abstract Algebra and Category Theory are two topics which I think may reflect this particularly well (though I haven't studied any category theory). The same goes for theoretical CS (which is really a branch of math).
2. There aren’t unique ways to slice up some interesting concepts, so there are some overlapping or even coinciding abstractions.
   1. We use specific abstractions because they have allowed us to achieve lots of progress on incorporation and generation of useful objects (e.g. definitions in abstract algebra that allow us to prove interesting theorems get widely adopted), but I strongly suspect there are sometimes alternative formulations that look quite different and still accomplish similar levels of success. In fact, I’ve heard examples of competing explanations of things that turned out to be proven equivalent. From the Wikipedia entry on the Church-Turing Thesis: 
      1. “Church, Kleene, and Turing proved that these three formally defined classes of computable functions coincide: a function is λ-computable if and only if it is Turing computable, and if and only if it is general recursive.”
3. Structure is a very important concept when it comes to abstraction. Every object that is an example of an abstraction must share the common features of the abstraction, and this necessity defines a basic structure of a generic example of the abstraction. Abstractions which involve more features, and more restrictive features, are more structured. Drawing on abstract algebra again: Groups are sets with additional structure, rings are groups with additional structure, and fields are rings with additional structure. Everything that is true in general with less structure remains true when additional structure is added, while the additional assumptions which generate more structure are often used to prove stronger statements to be true in general for objects with that structure. (The Wikipedia section on Basic Concepts in Abstract Algebra also describes this idea well.)
   1. So far, I've mostly explained how abstractions can be derived by looking at specific examples and extracting commonalities. This discussion of structure highlights an alternate way to derive abstractions: Start from an abstraction you already know, and add or remove structure. Of course, your choice of what structure to add or remove should be informed by the usefulness of the resulting abstraction.
   2. The aspects of specific examples that aren't pinned down by the abstract structure are the degrees of freedom that can vary between examples.
4. Another way of framing the value of abstractions is that they compress information, and this compressed information is often easier to work with. 
5. A pretty quote, paraphrased from my abstract algebra professor (Robert Friedman): "An abstraction is a way of calling many things by one name."

Further resources on abstraction:

1. Two 3blue1brown videos:
   1. Group theory, abstraction, and the 196,883-dimensional monster
   2. 8:20-11:02 in this other 3b1b video, on structuring math explanations
2. Wikipedia page on abstraction
3. The LessWrong Abstraction tag
4. All proof-based math and theoretical computer science
5. The world: once you know to look for it, you see abstraction everywhere!

1. ^{^}

   This definition combines components from the Wikipedia page on abstraction, John Wentworth's writing on abstraction, and my own interpretation.

2. ^{^}

   That is, every quadratic equation with coefficients in the complex numbers has two solutions in the complex numbers.

3. ^{^}

   Here, a = 1, b = 0, and c = -1. Plugging these values into the quadratic formula yields x = 1 and x = -1.

4. ^{^}

   Some of John's examples show that you need not care about all of the specific objects that an abstraction unifies - in fact, sometimes you only care about one of the objects. For instance, in the map of NYC example, the degrees of freedom that arise from moving from the actual streets to their representations in the map are things like "street width, potholes, power lines and water mains, building facades, signs and stoplights, etc." So the abstraction unifies all the possible versions of NYC streets with different widths, potholes, power lines, etc. However, we don't care about all these different versions - we only care about the real version. In these cases, the value of the abstraction doesn't come from its unification of many specific objects, but rather from its compression of the description of the single object we care about into a form that is easier to work with.

5. ^{^}

   Of course, our use of abstractions to shape the world isn't always positive. Most people regularly use products that are sourced via factory farming and burning fossil fuels, and the fact that we can use these products without seeing their production processes makes it very easy to indirectly contribute harm to animal welfare and the climate. These are just two examples, and there are countless others.

6. ^{^}

   It isn't really a matter of needing to appreciate examples before starting to appreciate an abstraction, but I think in many cases, you slowly gain an appreciation for the abstraction as you see and come up with more and more examples. It may actually take quite a few examples before you stop seeing new interesting instantiations of the abstraction.

7. ^{^}

   In some cases, like the sets-groups-rings-fields example under abstract algebra, this is because the sub-bullet is a variant of the parent bullet abstraction with additional structure. See the discussion of structure in the Miscellaneous section.

8. ^{^}

   This is kind of just a list of some of my favorite stories, but thinking about the specific ways they instantiate this abstraction helps me remember many of the specific things their creators did to make the stories so great.

9. ^{^}

   If you've completed these stories and want to know what specifically I'm referring to, feel free to ask in a comment. I had a bit of trouble with spoiler formatting so I tried to avoid spoilers, but I know that may have made it hard to know what I was referring to in some cases.

10. ^{^}

    One of the best episodes of TV I've ever seen.

11. ^{^}

    Sanderson's First Law is closely related to the "Have answers to the question 'Why?' as often as possible" abstraction, and his Third Law is closely related to the "Make story components as interconnected as possible" abstraction. I read about Sanderson's Three Laws before crystallizing those abstractions in my head, so they probably helped me do that.