This was the application I used to get into the upcoming developmental interpretability MATS stream. It is essentially a more polished version of this dialogue

Abstract

I investigated epoch-wise critical periods in neural networks from a singular learning theory lends. Hypothesizing that the cause has to do with a monotonic increasing relationship between epochs and temperature leading to periods at which, interpreting SGD as a kind of MCMC sampler, poor mixing occurs, resulting in SGD’s stationary distribution occupying a region of parameter space that doesn’t include the best parameter. This theory was experimentally supported by watching the RLCT increase only during the critical epochs, and showing we can increase when the critical period occurs by decreasing the batch size, a quantity with a far more straightforward relationship to the sampling temperature.

Introduction

I have argued in both a recent post, and dialogue that singular learning theory applied to reinforcement learning and neuroscience could serve as a bridge between the two, and allow for formally verifiable alignment between AI and human interests. In order to accomplish this goal, we need to actually know how to apply singular learning theory to developmental psychology and neuroscience.

Many animals that perform significant within-lifetime learning undergo critical periods, and so too do neural networks when trained on the appropriate tasks with the appropriate settings. If we hope to expand the theory of singular learning theory to developmental psychology and neuroscience, the study of in-silico critical periods therefore provides a well-defined and likely simple sub-problem with which to study.

Not only are the existence of critical periods impactful for the theory of neuroscience, but they're also impactful for asking about how the theory of singular learning generalizes to non-iid distributions. Critical periods arise due to distribution shifts in the training data, a major component of the modern language model fine-tuning paradigm. Those in the paper I build on here also occur epoch-wise, similarly making progress on the question of how to factor epochs into the framework of SLT.

The paper Critical Learning Periods in Deep Networks (Achille et al., 2019) is able to mimic early-childhood/infant cataract-caused permanent “amblyopia” (a weakening in the vision of an eye) by training image classifiers on first a blurred version of CIFAR-10 for a number of epochs, and then the sharp version of CIFAR-10 for the rest of the epochs. They witness a distinct drop-off, and then leveling off of the resulting accuracy on the original CIFAR-10, representing a critical period whereby no sharpness before a certain epoch leads to a poor solution.

Here I propose an argument about how these results may be consistent with singular learning theory, and present two experiments which are consistent with this argument.

The argument

Lets grant that increasing epochs can be thought of as decreasing temperature (or increasing inverse temperature $\beta$), and that SGD can be well modeled as a Gibbs sampler of the posterior distribution 

 and that this is dominated by the phase with the lowest free energy 

 Suppose we have two phases: The phase we get when training only on blurred images, and the phase we get when training on sharp images, and that for high temperature (low $\beta$) both of these phases look the same, in the sense that it is easy for a local samplers of the posterior distribution like gradient descent to traverse between them. But for high noise this is not so easy, and local samplers of the posterior distribution like gradient descent tend to get stuck inside one or the other phases.

Then as we decrease the temperature (increase $\beta$), we will predict a phase transition where if gradient descent is around one of the phases, it remains in that phase, and if its in the other phase, it remains in the other phase. This point therefore marks the end of the critical period of our model. If before/during this point we only saw blurry images, then we'd stay in the blurry-specific phase even when training on sharp images. If before/during this point we saw sharp images, then we'd be able to transition to the sharp phase before the no-return point.

If epochs, and the batch size both control the temperature of the model, and smaller epochs & batches correspond to larger temperatures, then we should expect that the no-return point will get pushed to a higher epoch if we decrease the batch size. This is the experiment that we run.

Experiment

I first replicated the paper, along with tracking the $\hat{\lambda }$ arrived at for each of the possible distribution transition points, to see if we could detect where the distribution shift happened. We were definitely able to replicate the paper, but $\hat{\lambda }$ seemed only loosely informative about where the critical point was. 

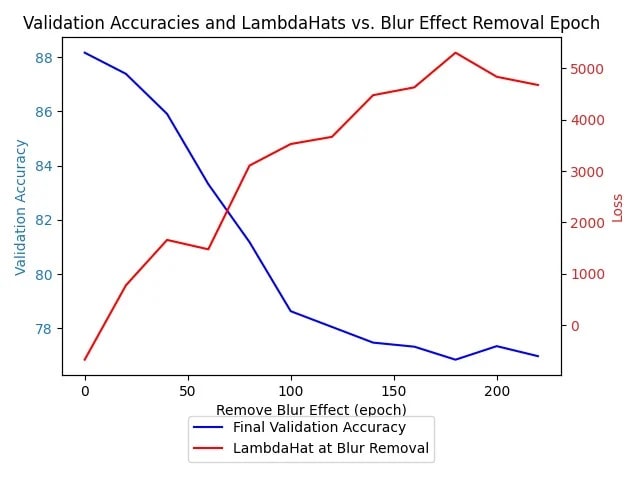
However the prediction that we can increase the amount of epochs it takes to finish the critical period by decreasing the batch size was vindicated. The above plot was produced with a batch size of 128, the below plot from a batch size of 64

We see a distinct increase in the epoch at which we have the kink in the graph, from between epochs 80 and 100 in the 128 graph to between epochs 120 and 160 in the second graph.

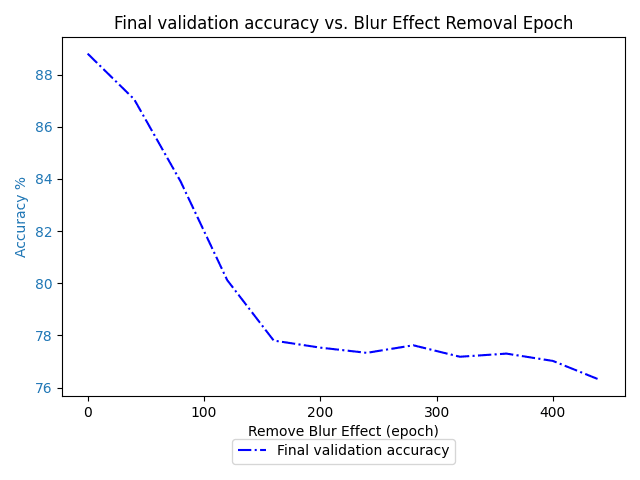
With a batch size of 256 we get 

for which its less obvious the kink in the graph got decreased, but it definitely didn't increase, and its rate of change is certainly a lot less after epoch 64 than before.

In this graph we also see a cleaner graph for lambdahat, this is because between the first graph and this one, I made some adjustements to some of the code for finding this quantity, so I don't think its fundamental, although it may be, since a larger batch size should produce a less noisy estimate.

Worries

One worry is that this story doesn't explain why you see a smooth decrease in loss as you change where the critical point happens. As if there's many different phases that you can get inside of which do decently well. Evidence for this is that on the way to the stationary distribution-transition epoch we see fairly reasonable & consistent estimates for $\hat{\lambda }$, suggesting at each of them we are at a different phase with a similar $\hat{\lambda }$.

Perhaps if we increased the resolution, we would in fact see a bunch of phase transitions. It seems likely we'd have to go down to batch level for that though, in my opinion. But I've been wrong in this project before.

Next steps

There are a few areas which these results open the way to further exploration in:

1. Finer grained analysis of the phase structure of the above. At what resolution must we record data for us to see this, if any?
2. What other epoch-wise phenomena can be explained via epoch vs batch-size tradeoffs, and the plausible connection to temperature?
   1. We could try to formally show the relation via mathematically tractable toy models
      1. Or even pseudo-theoretical toy problems like toy models of superposition, we could fit a temperature parameter to the empirical frequency distribution we get for a ground truth on just what the relation between batch, epoch, and temperature is.
   2. Perhaps epoch wise double descent is modulated through beta. If so, you should also see batch size double descent.
      1. If so, unlike in data double descent, where increasing the amount of data but keeping the phase constant can still decrease your expected bayesian generalization, I don't think there's a term in the expecteed bayesian generalization for $\beta$, so the only way it can change is by changing phases.
3. Further exploration of critical periods. This is certainly not the last word on them. For example, we are still unable to predict when critical periods occur, there are other control parameters we could mess around with having to do with the optimizer
4. Perhaps the simplest: Plotting the equi-temperate batch size vs epoch curve for a variety of problems with similar temperature varying controls, and checking whether the functional forms or even particular tradeoff parameters are similar.
5. Further exploration of more general varieties of mid-training distribution shifts.