The reward landscape of deep reinforcement learning models is probably pretty insane. Perhaps not insane enough to not be liable to singular learning theory-like analysis, since there’s always some probability of doing any sequence of actions, and those probabilities change smoothly as you change weights, so the chances you execute a particular plan change smoothly, and so your expected reward changes smoothly. So maybe there’s analogies to be made to the loss landscape.
I'm excited (and worried) about pursuing Whole Brain Emulation. I think that being able to study such an emulation to get a better idea about human values and human-human alignment successes and failures would be a boon. I also think finding a simplified brain-inspired AI with the useful aspects of the brain and also the useful aspects of current deep learning techniques would potentially be key for a pivotal act, or at least enforcing a delay long enough to figure out something better.
I rather suspect we're going to find ourselves in a transitional mixed-up muddle of many semi-aligned not-quite-trustworthy variants on ML models, which will not quite be good enough for anything approaching a pivotal act, but might be good enough for awkwardly muddling through on a Superalignment-type agenda. My best guess is that knowing more about the positive aspects of the brain could be quite helpful to humanity at such a juncture.
So I'm trying to figure out things like: "How is it that the general learning hardware of the cortex ends up with such specific and consistent-across-individuals localizations of function?"
One significant worry here would be that bounds from (classical) learning theory seem to be pretty vacuous most of the time. But I'm excited about comparing brains and learning algos, also see many empirical papers.
I'm hopeful that SLT's bounds are less vacuous than classical learning theoretic bounds, partially because non-equilibrium dynamics seem more tractable with such dominating singularities, and partially because all the equations are equality relations right now, not bounds.
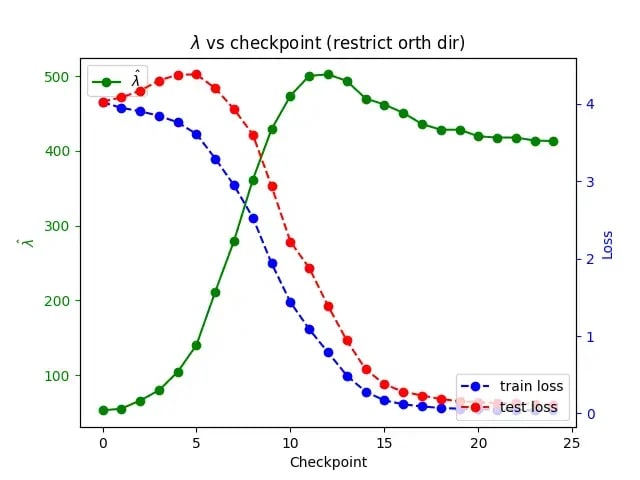
A comment I made while explaining why I was excited about the above picture to someone:
The timing of the plateau seems very accurate, the RLCT seems smooth & consistent, The test loss goes up as the RLCT increases faster than the train decreases (as would be predicted byBg=L+λ/n), (I did the math here wrong, 1. the estimate doesn't make sense between phases, and 2. If you go through the math, Bg' is very much not sensitive to small increases or decreases in lambda), this was done on a clearly not made for this particular situation model, rather than a bespoke model, we see that once the RLCT starts to decrease from its peak, the train loss doesn't move very much.
As far as I can tell, all lots of qualitative predictions of SLT's relating to how lambda will interact with generalization and test losses are shown in this picture, and the model is a model someone thought of to do something completely different.
The philosophy behind infra-bayesianism, and Vanessa's learning-theoretic alignment agenda seems very insightful to me. However, the giant stack of assumptions needed to make the approach work, and the ontology-forcing nature of the plan leave me unsettled. The path of singular learning theory has recently seen enough empirical justification to excite me. I'm optimistic it can describe brains & machine learning systems, and I describe my hope that this can be leveraged into alignment guarantees between the two, becoming an easier task as whole brain emulation develops.
Introduction
Imagine a world where instead of humanity wandering together blindly down the path of cobbled together weird tricks learned off the machine learning literature, with each person trying to prepare for the bespoke failure-mode that seems most threatening to them (most of whom are wrong).
That instead we lived in the world where before heading down we were given a map and eyes to see for ourselves the safest path, and the biggest and most dangerous cliffs, predators, and dangers to be aware of.
It has always seemed to me that we get to the second world once we can use math for alignment.
The left: Our situation. The right: Our situation if we had math for alignment. Generated with DALL·E 3.
For a long time I thought using math for alignment was essentially a non-starter. Deep learning is notoriously resistant to successful theories, I'm pessimistic that the approach of the Machine Intelligence Research Institute will take too much time, and the most successful mathematical theory of intelligence and alignment--infra-Bayesianism--rests on a stack of assumptions and mathematical arguments too high, too speculative, and too normative for me to be optimistic about. So I resigned myself to the lack of math for alignment.
I had previously known about singular learning theory, and gone to the singular learning theory conference in Berkeley. But after thinking about the ideas, and trying to implement some of the processes they came up with myself, and getting not so great results[3], I decided it too was falling for the same traps as infra-Bayesianism, lying on a giant stack of mathematical arguments, with only the most tentative contact with empirical testing with real world systems. So I stopped following it for a few months.
Looking at these new results though, it seems promising.
But its not natively a theory of alignment. Its an upgraded learning theory. How does that solve alignment?
Well, both the human brain & machine learning systems are learning machines, trained using a mix of reinforcement & supervised learning. If this theory were to be developed in the right way (and this is where the hope comes in), we could imagine relating the goals of the results of one learning process to the goals of a different learning process, and prove a maximal deviation between the two for a particular setup. If one of those learning systems is a human brain, then we have just gotten an alignment guarantee.
Hence my two main hopes for alignment[4]: whole brain emulation, and a learning-theoretic-agenda-like developmental track for singular learning theory.[5]
Interpretability, and other sorts of deep learning science seem good to the extent it helps with getting singular learning theory (or some better version of it) to the state where its able to prove such alignment-relevant theorems.
This task is made easier to the extent we have better whole brain emulation. And becomes so easy that we don't even need the singular learning theory component if we have succeeded in our whole brain emulation efforts.[6]
It seems like it'd be obvious to you, the reader, why whole brain emulation gives me hope[7]. But less obvious why singular learning theory gives me hope, so I will explain in much of the rest of this post why the latter is true.
Singular learning theory
Feel free to skip these next three paragraphs, or even instead of reading my description, read Jesse's or read pre-requisite 3. My goal is less to explain what singular learning theory is, and more to give an idea about why I'm excited about it.
Singular learning theory fills a gap in regular learning theory, in particular, regular learning theory assumes that the parameter function map of your statistical model is one-to-one, and intuitively your loss landscape has no flat regions.[8]
Singular learning theory handles the case where this is not true, which occurs often in hierarchical models, and (as a subset) deep neural networks. And in broad strokes by bringing in concepts from algebraic geometry in order to rewrite the KL divergence between the true model and parameters into a form that is easier to analyze.
In particular, it anticipates two classes of phase transitions during the development of models, one of which is that whenever loss suddenly goes down, the real-log-canonical-threshold (RLCT), a algebraic geometry derived metric for complexity, will go up.[9]
Its ultimately able to retrodict various facts about deep learning, including the success of data scaling, parameter scaling, and double descent, and there has been recent success in getting it to give predictions about phenomena in limited domains. Most recently, Nina Rimsky and Dmitry Vaintrob's Investigating the learning coefficient of modular addition: hackathon project where the two were able to verify various assertions about the RLCT/learning coefficient/^λ/Watanabe-Lau-Murfet-Wei estimate. Getting the most beautiful verification of a theoretical prediction in my lifetime
Chart of estimated ^λ over training for an MLP trained on modular addition mod 53. Checkpoints were taken every 60 batches of batch size 64. Hyperparameters for SGLD are γ=5, ϵ=0.001. The search was restricted to directions orthogonal to the gradient at the initialization point to correct for measurement at non-minima. [caption text from the original post]
As I said, singular learning theory makes the prediction that during phase transitions, the loss of a model will decrease while the RLCT (λ) will increase. Intuitively, this means, when you switch model classes you switch to a model class that fits the data better and is more complicated. Above, we see exactly this.
We investigate phase transitions in a Toy Model of Superposition (TMS) using Singular Learning Theory (SLT). We derive a closed formula for the theoretical loss and, in the case of two hidden dimensions, discover that regular k-gons are critical points. We present supporting theory indicating that the local learning coefficient (a geometric invariant) of these k-gons determines phase transitions in the Bayesian posterior as a function of training sample size. We then show empirically that the same k-gon critical points also determine the behavior of SGD training. The picture that emerges adds evidence to the conjecture that the SGD learning trajectory is subject to a sequential learning mechanism. Specifically, we find that the learning process in TMS, be it through SGD or Bayesian learning, can be characterized by a journey through parameter space from regions of high loss and low complexity to regions of low loss and high complexity.
In online learning and reinforcement learning, the theory typically aims to derive upper and lower bounds on "regret": the difference between the expected utility received by the algorithm and the expected utility it would receive if the environment was known a priori. Such an upper bound is effectively a performance guarantee for the given algorithm. In particular, if the reward function is assumed to be "aligned" then this performance guarantee is, to some extent, an alignment guarantee. This observation is not vacuous, since the learning protocol might be such that the true reward function is not directly available to the algorithm, as exemplified by DIRL and DRL. Thus, formally proving alignment guarantees takes the form of proving appropriate regret bounds.
If the principles of singular learning theory can be extended to reinforcement learning, and we get reasonable bounds for the generalization behavior of our model, or even exact claims about the different forms the value-equivalents inside our model will take as it progresses during training, we can either hope to solve a form of what can roughly be known as inner alignment--getting our model to consistently think & act in a certain way when encountering the deployment environment.
It seems reasonable to me to think we can in fact extend singular learning theory to reinforcement learning. The same sorts of deep learning algorithms work very well on both supervised and reinforcement learning, so we should expect the same algorithms have similar reasons for working on both, and singular learning theory gives a description of why those deep learning algorithms do well in the supervised learning case. So we should suspect the story for reinforcement learning follows the same general strokes[10].
If you like performance guarantees so much, why not just work on infra-Bayesianism?
Vanessa's technique was to develop a theory of what it meant to do good reasoning in a world that is bigger than yourself, and also requires you to do self-modeling. Then (as I understand it) prove some regret bounds, make a criterion for what it means to be an agent, and construct a system with a low bound on the satisfaction of the utility function of the agent that is most immediately causally upstream of the deployed agent.
This seems like a really shaky construction to me, mainly because we do not in fact have working in-silico examples of the agents she's thinking about. I'd be much happier with taking this methodology, and using it to prove bounds on actual real life deep learning systems' regret (or similar qualities) under different training dynamics.
I also feel uneasy about how it goes from theory about how values work (maximizing a utility function) to defining that as the success criterion[11]. I'd be more comfortable with a theory which you could apply to the human brain, and naturally derive a utility function (or other value format). Just by looking at how brains are built and developed. In the case that we're wrong about our philosophy of values, this seems more robust. And to the extent multiple utility functions can fit our behavior accounting for biases and lack of extensive reflection, having a prior over values informed by the territory (i.e. the format values are in in the brain) seems better than the blunt instrument of Occam's razor applied directly to the mapping from our actual and counterfactual actions to utility functions.
Of all the theories that I know of, singular learning theory seems the most adequate to the task. It both is based on well-proven math, it has and will continue to have great contact with actual systems, it covers a very wide range of learning machines, which includes human brains (ignoring the more reinforcement learning like aspects of human learning for now) & likely future machines (again ignoring reinforcement learning), and the philosophical assumptions it makes are far more minimalist than those of infra-Bayesianism.
The downside of this approach is singular learning theory says little right now about reinforcement learning. However, as I also said above, we see the same kinds of scaling dynamics in reinforcement learning as we do in supervised learning & the same kinds of models work in both cases, so it'd be pretty weird if they had very different reasons for being successful. Singular learning theory tries to explain the supervised learning case, so we should expect it or similar methods be able to explain the reinforcement learning case too.
Another downside is it not playing well with unrealizability. However, I'm told there hasn't been zero progress here, its an open problem in the field, and again, neural networks often learn in unrealizable environments, as far as I know, we see similar enough dynamics that I bet singular learning theory is up for the task.
Whole brain emulation
The human brain is almost certainly singular[12], has a big learning from scratch component to it, and singular learning theory is very agnostic about the kinds of models it can deal with[13], so I assert singular learning can deal with the brain. Probably not to help whole brain emulation all that much, but given data whole brain emulation gives us about the model class that brains fall into, the next hope is to use this to make nontrivial statements about the value-like-things that humans have. Connecting this with the value-like-things that our models have, we can hopefully (and this is the last hope) use singular learning theory to tell us under what conditions our model will have the same values-like-things that our brains have.
Fears
Wow! That's a lot of hopes. I'm surprised this makes you more hopeful than something simple like empirical model evaluations
Singular learning theory, interpretability, and the wider developmental interpretability all seem useful for empirically testing models. I'm not hopeful just because of the particular plan I outline above, I'm hopeful because I see a concrete plan at all for how to turn math into an alignment solution for which all parts seem to be useful even if not all of my hopes turn out correct.
I'm skeptical that something like singular learning theory continues to work as the model becomes reflective, and starts manipulating its training environment.
I am too. This consideration is why our guarantees should occur early in training, be robust to continued training, and be reflectively stable. Human-like values-like-things should be reflectively stable by their own lights, though we won't actually know until we actually see what we're dealing with here. So the job comes down to finding a system which puts them into our model early in training, keeps them throughout training, and ensures by the time reflection is online, the surrounding optimizing machinery is prepared.
Put another way: I see little reason to suspect the values-like-things deep learning induces will be reflectively stable by default. Primarily because the surrounding optimizing machinery is liable to give strange recommendations in novel situations, such as reflective thought becoming active[14]. So it does in fact seem necessary to prepare that surrounding optimizing machinery for the event of reflection coming online. But I'm not so worried about the values-like-objects being themselves disastrously suicidal once we know they're similar enough to those of humans.
Nate and possibly Eliezer would say this is important to know from the start. I would say I'll cross that bridge once I actually know a thing or two what values-like-thing, and surrounding machinery I'll be dealing with.
Why reinforcement learning? Shouldn't you focus on supervised learning, where the theory is clear, and we're more likely to get powerful models soon?
Well, brains are closer to reinforcement learning than supervised learning, so that's one reason. But yeah, if we can get a model which while supervised, we prove statements about values-like objects for, then that would be a good deal of the way there. But not all the way there, since we'd still be confused when looking at our brains.
Singular learning theory seems liable to help capabilities. That seems bad.
I will quote myself outlining my position on a related topic, which generalizes to the broader problem of developing a theory of deep learning:
Mostly I think that [mechanistic interpretability] is right to think it can do a lot for alignment, but I suspect that lots of the best things it can do for alignment it will do in a very dual-use way, which skews heavily towards capabilities. Mostly because capabilities advances are easier and there are more people working on those.
At the same time I suspect that many of those dual use concerns can be mitigated by making your [mechanistic interpretability] research targeted. Not necessarily made such that you can do off-the-shelf interventions based on your findings, but made such that if it ever has any use, that use is going to be for alignment, and you can predict broadly what that use will look like.
This also doesn't mean your [mechanistic interpretability] research can't be ambitious. I don't want to criticize people for being ambitious or too theoretical! I want to criticize people for producing knowledge on something which, while powerful, seems powerful in too many directions to be useful if done publicly.
My plan above is a good example of an ambitious & theoretical but targeted approach to deep learning theory for alignment.
Why singular learning theory, and not just whole brain emulation?
Firstly, as I said in the introduction, it is not obvious to me that given whole brain emulation we get aligned superintelligence, or are even able to perform a pivotal act. Recursive self improvement while preserving values may not be easy or fast (though you can always make the emulation faster). Pivotal acts done by such an emulation likely have difficulties I can't see.
However, I do agree that whole brain emulation alone seems probably alignment complete.
My main reason for focusing on both is that they feel like two different sides of the same problem in the sense that progress in whole brain emulation makes us need less progress in singular learning theory, and vice versa. And thinking in terms of a concrete roadmap makes me feel more like I'm not unintentionally sweeping anything important underneath any rugs. The hopes I describe have definite difficulties, but few speculative difficulties.
It seems difficult to get the guarantees you talk about which are robust to ontology shifts. Values are in terms of ontologies. Maybe if a model's ontology changes, its values will be different from the humans'
This is something I'm worried about. I think there's hope that during ontology shifts, the meta-values of the models will dominate what shape the model values take into the new ontology, and there won't be a fine line between the values of the human and the meta-values of the AI. There's also an independent hope that we can have a definition of values that is just robust to a wide range of ontology shifts.
So what next for singular learning theory and whole brain emulation?
I currently don't know too much about whole brain emulation. Perhaps there are areas they're focusing on which aren't so relevant to my goals here. For example, if they focus more on the statics of the brain than the dynamics, then that seems naively inefficient[15] because the theorem I want talks about the dynamics of learning systems and how those relate to each other.
Singular learning theory via Timaeus seems to mostly be doing what I want them to be doing: testing the theory on real world models, and seeing how to relate it to model internals via developmental interpretability. One failure-mode here is they focus too much on empirically testing it, and too little on trying to synthesize their results into a unified theory. Another failure-mode is they focus too much on academic outreach, and not enough on actually doing research. And then the academics they do outreach to don't really theoretically contribute that much to singular learning theory.
I'm not so worried about the first failure-mode, since everyone on their core team seems very theoretically inclined.
It seems like a big thing they aren't looking into is reinforcement learning. This potentially makes sense. Reinforcement learning is harder than supervised learning. You need some possibly nontrivial theoretical leaps to say anything about it in a singular learning theory framework. Even so, it seems possible there is low-hanging fruit in this direction. Similarly for taking current models of the brain
Of course, I expect the interests of Timaeus and myself will diverge as singular learning theory progresses, and there are pretty few people working on developing the theory right now. So it seems a productive use of my efforts.
Acknowledgements
Thanks to Jeremy Gillen, and David Udell for great comments and feedback! Thanks also to Nicholas Kees, and the Mesaoptimizer for the same.
Note I didn't read this, I watched the singular learning theory primer videos, but those seem longer than the series of LessWrong posts, and some have told me they're a good intro.
If I remember correctly, the reason for the not great results was because the random variable we were estimating had a too high variance to actually correlate with another quantity we were trying to measure in our project.
Ultimately hoping to construct a theorem of the form
Given agent Alice with architecture Vtrained with reward model RA in environment EA and agent Bob with architecture S trained with reward model RB in environment EB, end up with value systems UA and UB respectively (not necessarily utility functions), and UA∼EAUB+ε for some definition of ∼EA that means something like Bob tries to achieve something like what Alice tries to achieve when in environment EA.
And where we can solve for Bob's reward model and environment taking Alice as being a very ethical human. Hopefully with some permissive assumptions, and while constructing a dynamic algorithm in the sense that Bob can learn to do good by Alice's lights for a wide enough variety of Alices that we can hope humans are inside that class.
Since, hopefully, if we have whole brain emulation it will be easy for the uploaded person or people to bootstrap themselves to superintelligence while preserving their goals (not a trivial hope!).
There is a different phase transition which occurs when the RLCT goes down, and some other quantity goes up. There are several candidates for this quantity, and as far as I know, we don't know which increase is empirically more common.
The reward landscape of deep reinforcement learning models is probably pretty insane. Perhaps not insane enough to not be liable to singular learning theory-like analysis, since there's always some probability of doing any sequence of actions, and those probabilities change smoothly as you change weights, so the chances you execute a particular plan change smoothly, and so your expected reward changes smoothly. So maybe there's analogies to be made to the loss landscape.
I'm told that Vanessa and Diffractor believe infra-Bayesianism can produce reflectively stable and useful quantilizers and worst-case optimizers over a set of plausible utility functions. I haven't looked at it deeply, but I'd bet it still assumes more ontology than I'm comfortable with, both in the sense that for this reason it seems less practical than my imagined execution of what I describe here, and it seems more dangerous.
In its current form it requires only that they be analytic, but ReLUs aren't, and empirically we see ignoring that aspect gives accurate predictions anyway.
Situational novelty is not sufficient to be worried, but during reflection the model is explicitly thinking about how it should think better, so if its bad at this starting out, and makes changes to its thought, if those changes are to what it cares about, they will not necessarily be corrected by further thought or contact with the world. So situational novelty leading to incompetence is important here.
A way it could be efficient is if its just so much easier to do statics than dynamics, you will learn much more about dynamics from all the static data you collect than you would if you just focused on dynamics.
