Observation to potentially connect this to some math that people might be more familiar with: when and are probability distributions, then , where is the cross-entropy.
Note that the cross entropy, (and thus ) is dependent on meaningless details of what events you consider the same vs different, but is not (as much), and when maximizing with respect to , this is the same maximization.
(I am just pointing out that KL divergence is a more natural concept than cross entropy.)
I think might also have a natural interpretation of something along the lines of "The probability that two consecutive samples from P are equal". This holds exactly for the uniform distribution, but only holds approximately for the Bernoulli distribution, so this is not a perfect heuristic.
Now, let's consider the following modification: Each hypothesis is no longer a distribution on , but instead a distribution on some coarser partition of . Now is still well defined
Playing around with this a bit, I notice a curious effect (ETA: the numbers here were previously wrong, fixed now):
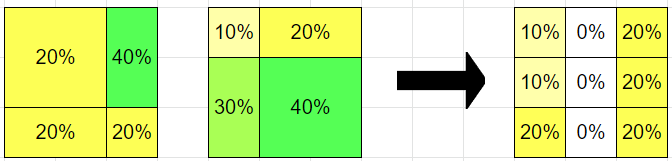
The reason the middle column goes to zero is that hypothesis A puts 60% on the rightmost column, and hypothesis B puts 40% on the leftmost, and neither cares about the middle column specifically.
But philosophically, what does the merge operation represent, which causes this to make sense? (Maybe your reply is just "wait for the next post")
I think your numbers are wrong, and the right column on the output should say 20% 20% 20%.
The output actually agrees with each of the components on every event in that component's sigma algebra. The input distributions don't actually have any conflicting beliefs, and so of course the output chooses a distribution that doesn't disagree with either.
I agree that the 0s are a bit unfortunate.
I think the best way to think of the type of the object you get out is not a probability distribution on but what I am calling a partial probability distribution on . A partial probability distribution is a partial function from that can be completed to a full probability distribution on (with some sigma algebra that is a superset of the domain of the partial probability distribution.
I like to think of the argmax function as something that takes in a distribution on probability distributions on with different sigma algebras, and outputs a partial probability distribution that is defined on the set of all events that are in the sigma algebra of (and given positive probability by) one of the components.
One nice thing about this definition is that it makes it so the argmax always takes on a unique value. (proof omitted.)
This doesn't really make it that much better, but the point here is that this framework admits that it doesn't really make much sense to ask about the probability of the middle column. You can ask about any of the events in the original pair of sigma algebras, and indeed, the two inputs don't disagree with the output at all on any of these sets.
Yeah, the right column should obviously be all 20s. There must be a bug in my code[1] :/
I like to think of the argmax function as something that takes in a distribution on probability distributions on with different sigma algebras, and outputs a partial probability distribution that is defined on the set of all events that are in the sigma algebra of (and given positive probability by) one of the components.
Take the following hypothesis :
If I add this into with weight , then the middle column is still nearly zero. But I can now ask for the probablity of the event in corresponding to the center square, and I get back an answer very close to zero. Where did this confidence come from?
I guess I'm basically wondering what this procedure is aspiring to be. Some candidates I have in mind:
- Extension to the coarse case of regular hypothesis mixing (where we go from P(w) and Q(w) to )
- Extension of some kind of Bayesian update-flavored thing where we go to then renormalize
- ETA: seems more plausible than
- Some kind of "aggregation of experts who we trust a lot unless they contradict each other", which isn't cleanly analogous to either of the above
Even in case 3, the near-zeros are really weird. The only cases I can think of where it makes sense are things like "The events are outcomes of a quantum process. Physics technique 1 creates hypothesis 1, and technique 2 creates hypothesis 2. Both techniques are very accurate, and the uncertainity they express is due to fundamental unknowability. Since we know both tables are correct, we can confidently rule out the middle column, and thus rule out certain events in hypothesis 3."
But more typically, the uncertainity is in the maps of the respective hypotheses, not in the territory, in which case the middle zeros seem unfounded. And to be clear, the reason it seems like a real issue[2] is that when you add in hypothesis 3 you have events in the middle which you can query, but the values can stay arbitrarily close to zero if you add in hypothesis 3 with low weight.
This maps the credence but I would imagine that the confidence would not be evenly spread around the boxes. With confidence literally 0 it does not make sense to express any credence to stand any taller than another as 1 and 0 would make equal sense. With a miniscule confidence the foggy hunch does point in some direction.
Without h3 it is consistent to have middle square confidence 0. With positive plausibily of h3 middle square is not "glossed over" we have some confidence it might matter. But because h3 is totally useless for credences those come from the structures of h1 and h2. Thus effectively h1 and h2 are voting for zero despite not caring about it.
Contrast what would happen with an even more trivial hypothesis of one square covering all with 100% or 9x9 equiprobable hypothesis.
You could also have a "micro detail hypothesis", (actually a 3x3) a 9x9 grid where each 3x3 is zeroes everywhere else than the bottom right corner and all the "small square locations" are in the same case among the other "big square" correspondents. The "big scale" hypotheses do not really mind the "small scale" dragging of the credence around. Thus the small bottom-right square is quite sensitive to the corresponding big square value and the other small squares are relatively insensitive. Mixing two 3x3 resolutions that are orthogonal results in a 9x9 resolution which is sparse (because it is separable). John Vervaeke meme of "sterescopic vision" seems to apply. The two 2x2 perspectives are not entirely orthogonal so the "sparcity" is not easy to catch.
The point I was trying to make with the partial functions was something like "Yeah, there are 0s, yeah it is bad, but at least we can never assign low probability to any event that any of the hypotheses actually cares about." I guess I could have make that argument more clearly if instead, I just pointed out that any event in the sigma algebra of any of the hypotheses will have probability at least equal to the probability of that hypothesis times the probability of that event in that hypothesis. Thus the 0s (and the s) are really coming from the fact that (almost) nobody cares about those events.
I agree with all your intuition here. The thing about the partial functions is unsatisfactory, because it is discontinuous.
It is trying to be #1, but a little more ambitious. I want the distribution on distributions to be a new type of epistemic state, and the geometric maximization to be the mechanism for converting the new epistemic state to a traditional probability distribution. I think that any decent notion of an embedded epistemic state needs to be closed under both mixing and coarsening, and this is trying to satisfy that as naturally as possible.
I think that the 0s are pretty bad, but I think they are the edge case of the only reasonable thing to do here. I think the reason it feels like the only reasonable thing to do for me is something like credit assignment/hypothesis autonomy. If a world gets probability mass, that should be because some hypothesis or collection of hypotheses insisted on putting probability mass there. You gave an edge case example where this didn't happen. Maybe everything is edge cases. I am not sure.
It might be that the 0s are not as bad as they seem. 0s seem bad because we have cached that "0 means you cant update" but maybe you aren't supposed to be updating in the output distribution anyway, you are supposed to do you updating in the more general epistemic state input object.
I actually prefer a different proposal for the type of "epistemic state that is closed under coarsening and mixture" that is more general than the thing I gesture at in the post:
A generalized epistemic state is a (quasi-?)convex function . A standard probability distribution is converted to an epistemic state through . A generalized epistemic state is converted to a (convex set of) probability distribution(s) by taking an argmin. Mixture is mixture as functions, and coarsening is the obvious thing (given a function , we can convert a generalized epistemic state over to a generalized epistemic state over by precomposing with the obvious function from to .)
The above proposal comes together into the formula we have been talking about, but you can also imagine having generalized epistemic states that didn't come from mixtures of coarse distributions.
I'm pretty sure that maximizing the expectation of any proper scoring rule will do all of these exactly the same, except maybe the last section because G has nice chaining properties that I'm too lazy to check for other scoring rules.
Do you think this has implications for there being other perfectly good versions of Thompson sampling etc? Or is this limited in implications because the argmax makes things too simple?
Yeah, I think Thompson sampling is even more robust, but I don't know much about the nice properties of Thompson sampling besides the density 0 exploration.
So a while ago, I was thinking about whether there was any way to combine probability distributions and by "intersecting" them; I wanted a distribution which had high probability only if both of and had high probability. One idea I came up with was . I didn't prove anything about it, but looking at some test cases it looked reasonable.
I was just about to suggest changing your belief aggregation method should be closer to this, but then I realized that it was already close in the relevant sense. Gonna be exciting to see what you might have to say about it.
The aggregation method you suggest is called logarithmic pooling. Another way to phrase it is: take the geometric mean of the odds given by the probability distribution (or the arithmetic mean of the log-odds). There's a natural way to associate every proper scoring rule (for eliciting probability distributions) with an aggregation method, and logarithmic pooling is the aggregation method that gets associated with the log scoring rule (which Scott wrote about in an earlier post). (Here's a paper I wrote about this connection: https://arxiv.org/pdf/2102.07081.pdf)
I'm also exited to see where this sequence goes!
Wait no, I'm stupid. What you do corresponds to , which is more like the union of hypotheses. You'd have to do something like to get the intersection, I think. I should probably think through the math again more carefully when I have more time.
Note that this is just the arithmetic mean of the probability distributions. Which is indeed what you want if you believe that P is right with probability 50% and Q is right with probability 50%, and I agree that this is what Scott does.
At the same time, I wonder -- is there some sort of frame on the problem that makes logarithmic pooling sensible? Perhaps (inspired by the earlier post on Nash bargaining) something like a "bargain" between the two hypotheses, where a hypothesis' "utility" for an outcome is the probability that the hypothesis assigns to it.
The place where I came up with it was in thinking about models that focus on independent dynamics and might even have different ontologies. For instance, maybe to set environmental policy, you want to combine climate models with economics models. The intersection expression seemed like a plausible method for that. Though I didn't look into it in detail.
Observation: If we want to keep everything in product form, then adding a constraint to the argmax can be seen as multiplying by an indicator function. I.e. if is 1 when is true and 0 when is false, then . Notably, we can't really do this with arithmetic maximization because then we would be taking the logarithm of 0, which is undefined.
I'm not sure how useful this is, because it doesn't really help with empirical approximation, as then you run into problems with multiplying by zero. But this might be nice; at least it seems to provide a quantitative justification for the view of probability distributions as being "soft constraints".
I have been posting a lot on instrumental geometric rationality, with Nash bargaining, Kelly betting, and Thompson sampling. I feel some duty to also post about epistemic geometric rationality, especially since information theory is filled with geometric maximization. The problem is that epistemic geometric rationality is kind of obvious.
A Silly Toy Model
Let's say you have some prior beliefs P0 at time 0, and you have to choose some new beliefs P1 for time 1. P0,P1∈ΔW are both distributions over worlds. For now, let's say you don't make any observations. What should your new beliefs be?
The answer is obvious, you should set P1=P0. However, if we want to phrase this as a geometric maximization, we can say
P1=argmaxP∈ΔWGw∼P0P(w).
This is saying, imagine the true world is sampled according to P0, and geometrically maximize the probability you assign to the true world. I feel silly recommending this because it is much more complicated that P1=P0. However, it gives us a new lens that we can use to generalize and consider alternatives.
For example, we can consider the corresponding arithmetic maximization,
P1=argmaxP∈ΔWEw∼P0P(w).
What would happen if we were to do this? We would find the world with the highest probability, and put all our probability mass on that world. We would anticipate that world, and ignore all the others.
This is a stupid way to manage our anticipation. Nobody is going around saying we should arithmetically maximize the probability we assign to the true world. (However, people are going around saying we should arithmetically maximize average utility, or arithmetically maximize our wealth.)
Not only does arithmetic maximization put all our anticipatory eggs in one basket, it also opens us up to all sorts of internal politics. If we take a world and add some extra features to it to split it up into multiple different worlds, this changes the evaluation of which world is most efficient to believe in. This is illustrating two of the biggest virtues of geometric rationality: proportional representation, and gerrymander resistance.
A Slightly Less Silly Toy Model
Now, lets assume we make some observation X⊆W, so we know that the real world is in X. We will restrict our attention to probability distributions that assign probability 1 to X. However, if we try to set
P1=argmaxP∈ΔW, P(X)=1Gw∼P0P(w),
we run into a problem. We are geometrically maximizing the same quantity as before, subject to the constraint that P(X)=1, but the problem is that the geometric expectation is 0 no matter what we do, because P(w)=0 for any w∉X.
However, this is easy to fix. Instead of requiring that P(X)=1, we can require that P(X)≥b, and take a limit as b approaches 1 from below. Thus, we get
P1=limb→1−argmaxP∈ΔW, P(X)≥bGw∼P0P(w).
Turns out this limit exists, and P1 corresponds exactly to Bayesian updating on the event X. Again, this is more complicated that just defining Bayesian updating like a normal person, so I am being a little obnoxious by treating this as an application of geometric rationality.
However, I think you can see the connection to geometric rationality in Bayesian updating directly. When I assign probability 1 to an event X that I used to assign probability 12, I have all this extra probability mass in X worlds. How should I distribute this probability mass across the X worlds? Bayesian updating recommends that I geometrically scale all the probabilities up by the same amount. Why are we scaling probabilities up rather than e.g. arithmetically increasing all the probabilities by the same amount?
Because we actually care about our probabilities in a geometric (multiplicative) way!
It is much worse to decrease your probability of the true world from .11 to .01 than it is to decrease your probability of the true world from .9 to .8. This is because the former is geometrically a much larger decrease.
Generalized Updates
This model stops being silly when we start using it for something new, where the geometric maximization actually helps. For that, we can consider updating on some more strange stuff. Imagine you want to update on the fact that X and Y are independent. How do you observe this? Well maybe you looked into the mechanism of how the world is generated, and see that there is no communication between the thing that generates X and the thing that generates Y. Or maybe you don't actually observe the fact, but you want to make your probability distribution simpler and easier to compress by separating out the X and Y parts. Or maybe X represents your choice, and Y represents your parents, and you want to implement a causal counterfactual via conditioning. Anyway, we have a proposal for updating on this.
P1=argmaxP∈ΔW, P(X)P(Y)=P(X∧Y)Gw∼P0P(w).
In general, we can enforce any restrictions we want on our new probability distribution, and geometric maximization gives us a sane way to update.
Aggregating Beliefs
Now let's say I have a bunch of hypotheses about the world. H is my set of hypotheses, and each hypothesis is a distribution on worlds, H⊆ΔW. I also have a distribution P∈ΔH, representing my credence on each of these hypotheses. How should interpret myself as having beliefs about the world, rather than just beliefs about hypotheses?
Well, my beliefs about the world are just argmaxQ∈ΔWGh∼PGw∼hQ(w). Again, I could have done this in a simpler way, not phrased as geometric maximization. However, I would not be able to do the next step.
Now, let's consider the following modification: Each hypothesis is no longer a distribution on W, but instead a distribution on some coarser partition of W. Now argmaxQ∈ΔWGh∼PGw∼hQ(w) is still well defined, and other simpler methods of defining aggregation are not. (The argmax might not be a single distribution, but it will be a linear space of distributions, and it will give a unique probability to every event in any of the sigma algebras of the hypotheses.)
I have a lot to say about this method of aggregating beliefs. I have spent a lot of time thinking about it over the last year, and think it is quite good. It can be used to track the difference between credence (probability) and confidence (the strength of your belief), and thinking a lot about it has also caused some minor shifts in the way I think about agency. I hope to write about it a bunch soon, but that will be in a different post/sequence.