Agenty things have the type signature (A -> B) -> A. In English: agenty things have some model (A -> B) which predicts the results (B) of their own actions (A). They use that model to decide what actions to perform: (A -> B) -> A.
In the context of causal DAGs, the model (A -> B) would itself be a causal DAG model - i.e. some Python code defining the DAG. Logically, we can represent it as:
… for some given distribution functions and .
From an outside view, the model (A -> B) causes the choice of action A. Diagrammatically, that looks something like this:
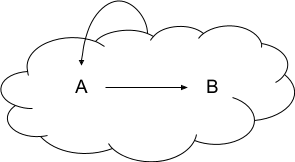
The “cloud” in this diagram has a precise meaning: it’s the model for the DAG inside the cloud.
Note that this model does not contain any true loops - there is no loop of arrows. There’s just the Hofstaderian “strange loop”, in which node A depends on the model of later nodes, rather than on the later nodes themselves.
How would we explicitly write this model as a Bayes net?
The usual way of writing a Bayes net is something like:
… but as discussed in the previous post, there’s really an implicit model M in there. Writing everything out in full, a typical Bayes net would be:
… with .
Now for the interesting part: what happens if one of the nodes is agenty, i.e. it performs some computation directly on the model? Well, calling the agenty node A, that would just be a term ... which looks exactly like a plain old root node. The model M is implicitly an input to all nodes anyway, since it determines what computation each node performs. But surely our strange loop is not the same as the simple model A -> B? What are we missing? How does the agenty node use differently from other nodes?
What predictions would (A -> B) -> A make which differ from A -> B?
Answer: interventions/counterfactuals.
Modifying M
If A is determined by a computation on the model , then is causally upstream of A. That means that, if we change - e.g. by an intervention - then A should change accordingly.
Let’s look at a concrete example.
We’ll stick with our (A -> B) -> A system. Let’s say that A is an investment - our agent can invest anywhere from $0 to $1. B is the payout of the investment (which of course depends on the investment amount). The “inner” model describes how B depends on A.
We want to compare two different models within this setup:
- A chosen to maximize some expected function of net gains, based on
- A is just a plain old root node with some value (which just so happens to maximize expected net gains for the we're using)
What predictions would the two make differently?
Well, the main difference is what happens if we change the model , e.g. by intervening on B. If we intervene on B - i.e. fix the payout at some particular value - then the “plain old root node” model predicts that investment A will stay the same. But the strange loop model predicts that A will change - after all, the payout no longer depends on the investment, so our agent can just choose not to invest at all and still get the same payout.
In game-theoretic terms: agenty models and non-agenty models differ only in predictions about off-equilibrium (a.k.a. interventional/counterfactual) behavior.
Practically speaking, the cleanest way to represent this is not as a Bayes net, but as a set of structural equations. Then we’d have:
However, this makes the key point a bit tougher to see: the main feature which makes the system “agenty” is that M appears explicitly as an argument to a function, not just as prior information in probability expressions.