The Problem
This post is an exploration of a very simple worry about the concept of utility maximisers - that they seem capable of explaining any exhibited behaviour. It is one that has, in different ways, has been brought up many times before. Rohin Shah, for example, complained that the behaviour of everything from robots to rocks can be described by utility functions. The conclusion seems to be that being an expected utility maximiser tells us nothing at all about the way a decision maker acts in the world - the utility function does not constrain. This clashes with arguments that suggest, for example, that a future humanity or AI would wish to self-modify its preferences to be representable as a utility function.
According to Wikipedia’s definition, a decision maker can be modelled as maximising expected utility if its preferences over mutually exclusive outcomes satisfy completeness, transitivity, continuity and independence. This is neat. However, it still leaves us with free choice in ordering over our set of mutually exclusive outcomes. The more outcomes we have, the less constrained we are by utility maximisation and when we look closely there are often a LOT of mutually exclusive outcomes, if we give ourselves truly free range over the variables in question.
In the context of thought around AI safety, introductions to these axioms have not denied this but added a gloss of something like ‘if you have a consistent direction in which you are trying to steer the future, you must be an expected utility maximizer’, in this case from Benya's post in 2012. Here the work done by ‘consistent direction’ seems to imply that you have reduced the world to a sufficiently low dimensional space of outcomes. Though I agree with this sentiment, it seems fuzzy. I hope to add some clarity to this kind of qualification. To put it another way, I want to see what restrictions we need to add to regain something like the intuitive notion of the maximiser and see if it is still sufficiently general as to be worth applying to theoretical discussions of agents.
Pareto Frontier of Concepts
A quick aside: Why do we want to use the idea of a utility maximiser? The explanation that comes to mind is that it is felt to be a concept that lies on the Pareto frontier of a trade-off between the explanatory power of a concept and the lack of troubling assumptions. I doubt this framing is new but I drew up a little diagram anyway.
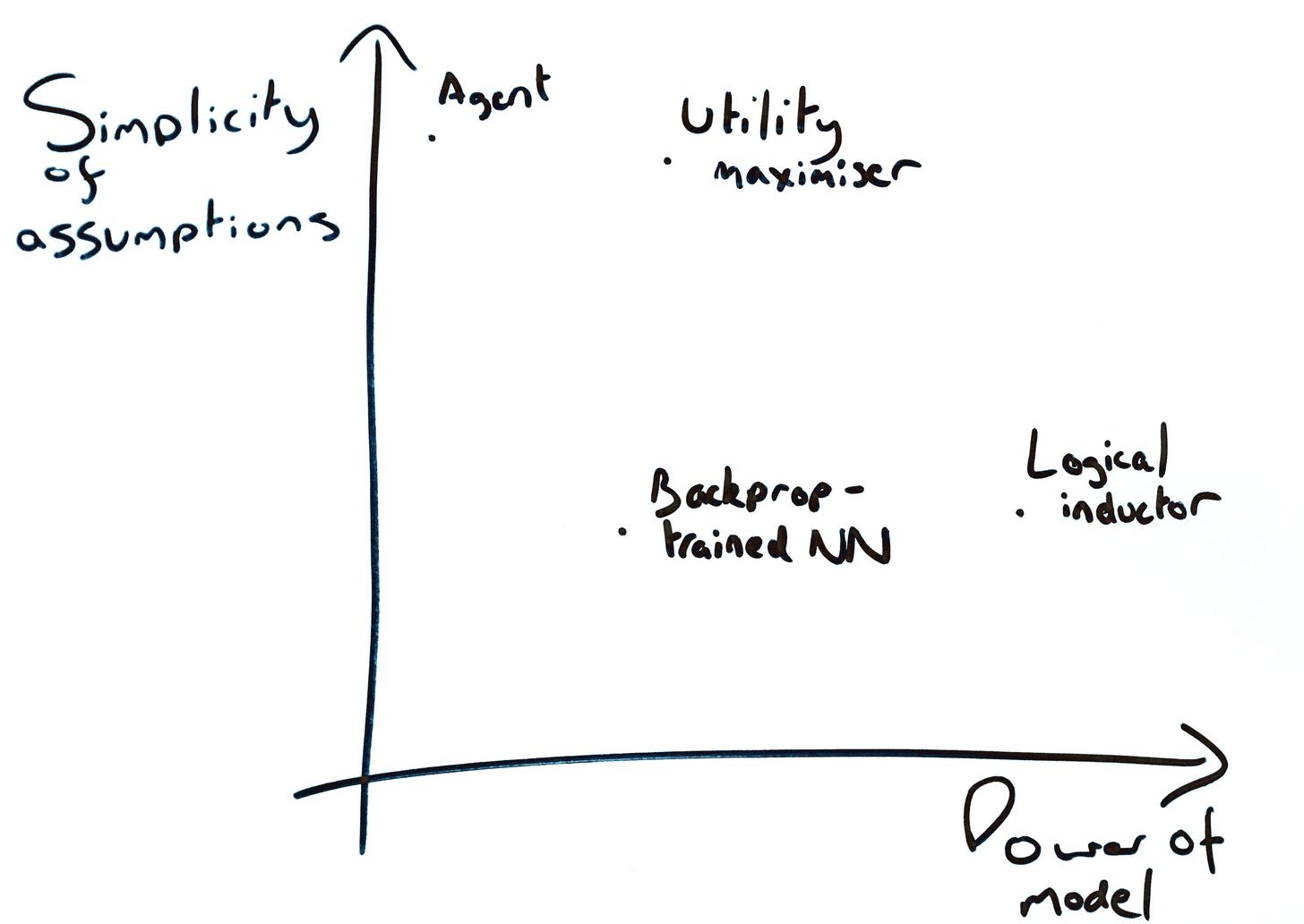
Explaining Too Much
What I want to do is move from considering utility functions in general to particular classes of utility functions. To begin, let's look at the first example, let's look at a canonical example of utilities being constraining - the Allais paradox. In the paradox it is shown that people have inconsistent preferences over money where the utilities involved are samples of the underlying utility function where the input is money, for concreteness, at a particular future time . In this case most humans can be shown to make decisions not compatible with any preference ordering.
When we construct this scenario we are imagining that people are in identical states when they are offered the various choices. However, we could instead construct these lotteries as being offered at distinct moments in time, and allow preferences over money to vary freely as time goes on. Now we are assuming instead the class of utility functions where the input is the pair (gain in money at current time , time). Importantly, a person can still make irrational decisions with respect to their individual utility function, but now there is no behaviour that can be ruled out by this abstraction.
The basic point is the obvious one that the class of potential utility functions decides the extent to which the utility function constrains behaviour. Note that even the first class of utility functions over money is extremely permissive - the Allais paradox only works because the possible outcomes in terms of money are identical, but in any scenario where the quantities involved in the lottery are different, one could make any set of decisions and remain free of inconsistency. I may for example have wildly different preferences for having £1, £1.01, £1.02 etc.. It is also important to note that we only need to have one such 'free' variable in our utility function to strip it of its predictive power.
Restricting Function Classes
The next question is whether it is possible to tighten up this theory so that it accords with my intuitive notion of a maximiser, and whether too much is lost in doing so.
One simple way is to reduce possible trajectories to a discrete space of outcomes - I want an aligned AI, I want to be alive in 20 years etc - and view all possible decisions as lotteries over this space. No arguments from me, but we certainly want a more expressive theory.
The example given in Eliezer's Stanford talk, which opens with an argument as to why advanced AIs will be utility maximisers, is that of a hospital trying to maximise the number of lives saved. Here we find the rather unsurprising result that one's preferences can be gainfully modelled as maximising expected utility... if they were already a linear function of some persistent real world variable.
What if we go beyond linear functions though? There certainly seems to be a space for 'near to a goal' functions, like radial basis functions, both in theoretical and practical uses of utility functions. What about cubics? Any polynomials? My instinct is to reach for some kind of notion of smooth preferences over a finite number of 'resources' which persist and remain similarly valued over time. This certainly does a lot of work to recover what we are assuming, or at least imagining, when we posit that something is a utility maximiser.
However, there seem to be nearly maximal examples of non-smoothness that still allow for a class of utility functions that constrain behaviour. For example, take the class of preferences over a rational number in which all I care about is the denominator when the number is in its simplest form. I could for example desire the greatest denominator: . In most situations, were these preferences over my store of dollars for example, this would seem to be outside the class of utility functions that would meaningfully constrain my action, since this function is not at all smooth over the resource in question. However, the are imaginable cases, such as when my action space is to multiply my bank account by a lottery of other rationals, in which a class of utility functions incorporating this sort of information represents a meaningful restriction on my behaviour.
A contrived example? Completely, but what this implies is that the real problem is not strictly in the way in which our function class is able to map 'real' variables to utility but in the way in which our decisions represent a restriction of our future outcome space.
Connecting Function Classes and Decision Spaces
The result is the perhaps obvious point that whether a class of utility functions constrains behaviour in a given situation is function not just of either the class in question or the type of actions available but a question of the extent to which our available actions are correlated with the possible. When this is true for all utility functions in the class we are considering, our utility function becomes capable of constraining behaviour (though there may still be cases where no course of action could not result from a utility function). This is more likely to happen when our objective must be a simple function of persistent real world states but it does not require this simplicity, as the above example shows.
To take an example of how this works in practice: in economics textbooks we will encounter a wide range of utility functions. These will of course determine the way that the agent behaves in the given scenario. More than this though, the very fact that these agents are utility maximisers feels as if it constrains their behaviour, not just because of the specific utility function but in the kind of calculating, maximising reasoning that it enforces. Under this analysis, the reason that it seems this way is that all utility functions that we might expect in such a scenario, whether logarithmic, quadratic, lexical, all are such that any given utility function, our actions will change the amount of utility we expect to be available. This is not because of the class of potential utility functions exactly, but because the action space/utility function class combination are such that the actions and changes in magnitude of available utility are always linked. (In this pedagogical case of course we come to expect this with good reason because the utility function/action space pair are selected to produce interesting interaction.)
What we need to find, for a given agent to be constrained by being a 'utility maximiser' is to consider it as having a member of a class of utility functions where the actions that are available to it systematically alter the expected utility available to it - for all utility functions within this class. This is a necessary condition for utility functions to restrict behaviour, not a sufficient one. Note that within almost any natural class there will be the degenerate utility function in which all results result in equal utility and therefore all actions are permissible - this must be deliberately excluded to make predictions. It is this notion of classes rather than individual utility functions, which saves my post (I hope) from total triviality.
What remains?
All this talk of restricting function classes is fine, and there is much more to say, but we're talking about selecting the class of possible utility functions as a modelling tool! We can restrict the class of functions that their utility function is allowed to be a part of, but if decision makers can employ a function from outside our allowed class and laugh at our Dutch books then what use is all this talk, and these abstractions?
Well, a few things. Firstly I hope this leads some people to clearer understanding of what is going on with utility functions - I feel I am now thinking more clearly about them, though only time will tell if this feeling lasts.
Second, when we make statements about utility functions being meaningful for an agent which wants to steer the future in a consistent direction, we have a more direct way of talking about this.
Third, there may be some ways in which such restrictions are natural for interesting classes of agents.
One thing to consider about a system, with respect to how we should model it, is whether we should expect a system to systematically acquire the capacity to control variables that are of relevance to it.
If I understand them correctly, systems which run according to active inference/predictive processing (of which humans may be a member) can be interpreted as maximising the power to predict observed variation (in this case entropy), presumably where variation is measured across a finite set of information streams. This may suggest that these systems naturally converge to methods of behaviour that are well modelled by utility functions of a particular class and so the abstraction of utility functions may regain meaning while still accurately describing such systems.
Sweeping the Floor
So what becomes of our rock that maximises its rock-like actions? Firstly, we can say that the class of utility functions needed to represent these 'decisions' is simply too broad to be consistently correlated with the minimal freedom of 'action' that a rock has, and thus our abstraction has no predictive power. Second, of course, is that thinking about utility in this way emphasizes that utility is a way of representing decisions. and a rock does not make decisions. How do we know? I'm not entirely sure, but it's not a question that can be offloaded to utility theory.
And what of our humans, and AIs, that may wish to modify themselves, in order to become truly consistent utility maximisers? Does this represent a likely happening? I think this may well still be true, for humans at least, but what is going on is not purely the result of utility functions but comes from the fact that humans seem to (a) organize their way of evaluating to situations to simpler outcome spaces so that there is a restriction of the space of utility functions that contains all of the possible ways in which humans value trajectories and (b) is such that all possible functions in this class require humans to take decisions which are consequential the evaluation of this utility function. In some ways this is very similar to the 'steering the future' hypothesis presented at the beginning but hopefully with some further clarification and operationalization of what this means.
My conclusions are getting shakier by the paragraph but it's posting day here at MSFP and so the flaws are left as an exercise to the reader.