Thankfully, almost all of the time the convex agents end up destroying themselves by taking insane risks to concentrate their resources into infinitesimally likely worlds, so you will almost never have to barter with a powerful one.
(why not just call them risk seeking / risk averse agents instead of convex/concave?)
I see the intuition here, but I think the actual answer on how convex agents behave is pretty messy and complicated for a few reasons:
- Otherwise convex agents might act as though resources are bounded. This could be because they assign sufficiently high probability to literally bounded universes or because they think that value should be related to some sort of (bounded) measure
- More generally, you can usually only play lotteries if there is some agent to play a lottery with. If the agent can secure all the resources that would otherwise be owned by all other agents, then there isn't any need for (further) lotteries. (And you might expect convex agents to maximize the probability of this sort of outcome.)
- Convex agents (and even linear agents) might be dominated by some possiblity of novel physics or similarly large breakthrough opening up massive amounts of resources. In this case, it's possible that the optimal move is something like securing enough R&D potential (e.g. a few galaxies of resources) that you're well past diminishing returns on hitting this, but you don't necessarily otherwise play lotteries. (It's a bit messier if there is competition for the resources opened up by novel physics.
- Infinite ethics.
True, they're naturally rare in general. The lottery game is a good analogy for the kinds of games they prefer; a consolidation, from many to few, and they can play these sorts of games wherever they are.
I can't as easily think of a general argument against a misaligned AI ending up convex though.
Well, if you make a convex misaligned AI, it will play the (metaphorical) lottery over and over again until 99.9999%+ of the time it has no power and resources left whatsoever. The smarter it is, the faster and more efficient it will be at achieving this outcome.
So unless the RNG gods are truly out to get you, in the long run you are exceedingly unlikely to actually encounter a convex misaligned AI that has accumulated any real amount of power.
Mm on reflection, the Holdout story glossed over the part where the agent had to trade off risk against time to first intersolar launch (launch had already happened). I guess they're unlikely to make it through that stage.
Accelerating cosmological expansion means that we lose, iirc, 6 stars every day we wait before setting out. The convex AGI knows this, so even in its earliest days it's plotting and trying to find some way to risk it all to get out one second sooner. So I guess what this looks like is it says something totally feverish to its operators to radicalize them as quickly and energetically as possible, messages that'll tend to result in a "what the fuck, this is extremely creepy" reaction 99% of the time.
But I guess I'm still not convinced this is true with such generality that we can stop preparing for that scenario. Situations where you can create an opportunity to gain a lot by risking your life might not be overwhelmingly common, given the inherent tension between those things (usually, safeguarding your life is an instrumental goal), and given that risking your life is difficult to do once you're a lone superintelligence with many replicas.
I can't as easily think of a general argument against a misaligned AI ending up convex though.
Most goals humans want you to achieve require concave-agent-like behaviors perhaps?
It’s difficult to trade with exponential agents
"Trade" between exponential agents could look like flipping a coin (biased to reflect relative power) and having the loser give all of their resources to the winner. It could also just look like ordinary trade, where each agent specializes in their comparative advantage, to gather resources/power to prepare for "the final trade".
"Trade" between exponential and less convex agents could look like making a bet on the size (or rather, potential resources) of the universe, such that the exponential agent gets a bigger share of big universes in exchange for giving up their share of small universes (similar to my proposed trade between a linear agent and a concave agent).
Maybe the real problem with convex agents is that their expected utilities do not converge, i.e., the probabilities of big universes can't possibly decrease enough with size that their expected utilities sum to finite numbers. (This is also a problem with linear agents, but you can perhaps patch the concept by saying they're linear in UD-weighted resources, similar to UDASSA. Is it also possible/sensible to patch convex agents in this way?)
However, convexity more closely resembles the intensity deltas needed to push reinforcement learning agent to take greater notice of small advances beyond the low-hanging fruit of its earliest findings, to counteract the naturally concave, diminishing returns that natural optimization problems tend to have.
I'm not familiar enough with RL to know how plausible this is. Can you expand on this, or anyone else want to weigh in?
Can you expand on this, or anyone else want to weigh in?
Just came across a datapoint, from a talk about generalizing industrial optimization processes, a note about increasing reward over time to compensate for low-hanging fruit exhaustion.
This is the kind of thing I was expecting to see.
Though, and although I'm not sure I fully understand the formula, I think it's quite unlikely that it would give rise to a superlinear U. And on reflection, increasing the reward in a superlinear way seems like it could have some advantages but would mostly be outweighed by the system learning to delay finding a solution.
Though we should also note that there isn't a linear relationship between delay and resources. Increasing returns to scale are common in industrial systems, as scale increases by one unit, the amount that can be done in a given unit of time increases by more than one unit, so a linear utility increase for problems that take longer to solve, may translate to a superlinear utility for increased resources.
So I'm not sure what to make of this.
Yeah, to clarify, I'm also not familiar enough with RL to assess exactly how plausible it is that we'll see this compensatory convexity, around today's techniques. For investigating, "Reward shaping" would be a relevant keyword. I hear they do some messy things over there.
But I mention it because there are abstract reasons to expect to see it become a relevant idea in the development of general optimizers, which have to come up with their own reward functions. It also seems relevant in evolutionary learning, where very small advantages over the performance of the previous state of the art equates to a complete victory, so if there are diminishing returns at the top, competition kind of amplifies the stakes, and if an adaptation to this amplification of diminishing returns trickles back into a utility function, you could get a convex agent.
- Though the ideas in this MLST episode optimization processes crushing out all serendipity and creativity suggest to me that that sort of strict life or death evolutionary processes will never be very effective. There was an assertion that it often isn't that way in nature. They recommend "Minimum Criterion Coevolution".
I was considering captioning the first figure "the three genders" as a joke, but I quickly realized it doesn't pass at all for a joke, it's too real. Polygyny (sperm being cheap, pregnancy being expensive) actually does give rise to a tendency for males of a species to be more risk-seeking, though probably not outright convex. And the correlation between wealth, altruism and linearity does kind of abstractly reflect an argument for the decreased relevance of this distinction in highly stable societies that captures my utopian nonbinary feelings pretty well.
The convex agent can be traded with a bit more than you think.
A 1 in 10^50 chance of us standing back and giving it free reign of the universe is better than us going down fighting and destroying 1kg as we do.
The concave agents are less cooperative than you think, maybe. I suspect that to some AI's, killing all humans now is more reliable than letting them live.
If the humans are left alive, who knows what they might do. They might make the vacuum bomb. Whereas the AI can Very reliably kill them now.
Alternate phrasing, "Oh, you could steal the townhouse at a 1/8billion probability? How about we make a deal instead. If the rng rolls a number lower than 1/7billion, I give you the townhouse, otherwise, you deactivate and give us back the world." The convex agent finds that to be a much better deal, accepts, then deactivates.
I guess perhaps it was the holdout who was being unreasonable, in the previous telling.
Or the sides can't make that deal because one side or both wouldn't hold up their end of the bargain. Or they would, but they can't prove it. Once the coin lands, the losing side has no reason to follow it other than TDT. And TDT only works if the other side can reliably predict their actions.
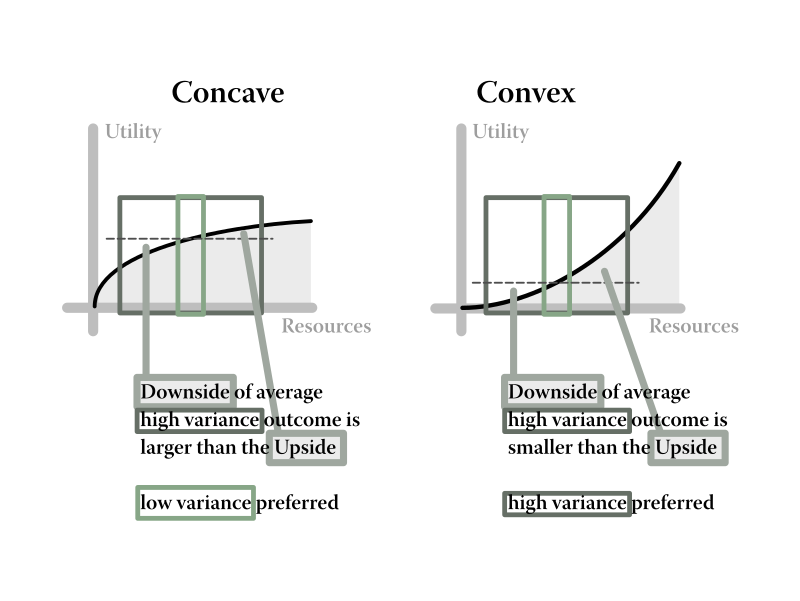
This seems to be talking about situations where a vector of inputs has an optimal setting at extremes (convex), in contrast to situations where the optimal setting is a compromise (concave).
I'm inclined to say it's a very different discussion than this one, as an agent's resource utility function is generally strictly increasing, so wont take either of these forms. The optimal will always be at the far end of the function.
But no, I see the correspondence: Tradeoffs in resource distribution between agents. A tradeoff function dividing resources between two concave agents (, where is the hoard being divided between them, ) will produce that sort of concave bulge, with its optimum being a compromise in the middle, while a tradeoff function between two convex agents will have its optima at one or both of the ends.
I hate the terms Concave and Convex in relation to functions.
Agreed.
the line (which should be considered to be the open side because integration makes the side below the line the solid side)
This is terrible: one pretty basic property you want in your definition describing the shape of functions is that it shouldn't change if you translate the function around.
Consider (for ). Pretty much the point of this definition is to be able to say it's the opposite kind as , but your choice wouldn't have that feature.
The "line at infinity" is a better choice for the imagined boundary. That's how we can think of parabolae as a kind of ellipse, for example.
if we called them decelerating (concave) or accelerating (convex) functions.
That'd be at least as confusing as the current terms for functions like or or .
No matter what the reward function, isn't a rational maximizer engaging in repeated play going to "end up" concave due to e.g Kelly Criterion? I would think convex agents would be sub-optimal/quickly self-destruct if you tried to create one and nature will basically never do so.
Lots of people think that. Occasionally because they are in a situation where the assumptions of Kelly don't hold (for example, you are not playing a repeated game), but more often because they confuse single bets (where Kelly maximizes log dollars) with repeated play (where Kelly maximizes total dollars).
In the long run, Kelly is optimal so long as your utility function is monotonic in dollars since it maximizes your total dollars.
From wikipedia
Whether it is possible to justify Kelly betting even when your utility is linear in money (SBF said it was for him) is very much an open research problem. There are various posts on this topic when you search LessWrong for "Kelly". I wouldn't assume Wikipedia contains authoritative information on this question yet.
These classifications are very general. Concave utility functions seem more rational than convex ones. But can we be more specific?
Intuitively, it seems a rational simple relation between resources and utility should be such that the same relative increases in resources are assigned the same utility. So doubling your current resources should be assigned the same utility (desirability) irrespective of how much resources you currently have. E.g. doubling your money while being already rich seems approximately as good as doubling your money when being not rich.
Can we still be more specific? Arguably, quadrupling (x4) your resources should be judged twice as good (assigned twice as much utility) as doubling (x2) your resources.
Can we still be more specific? Arguably, the prospect of halfing your resources should be judged being as bad as doubling your resources is good. If you are forced with a choice between two options A and B, where A does nothing, and B either halves your resources or doubles them, depending on a fair coin flip, you should assign equal utility to choosing A and to choosing B.
I don't know what this function is in formal terms. But it seems that rational agents shouldn't have utility functions that are very dissimilar to it.
The strongest counterargument I can think of is that the prospect of losing half your resources may seem significantly worse than the prospect of doubling your resources. But I'm not sure this has a rational basis. Imagine you are not dealing with uncertainty between two options, but with two things happening sequentially in time. Either first you double your money, then you half it. Or first you half your money, then you double it. In either case, you end up with the same amount you started with. So doubling and halfing seem to cancel out in terms of utility, i.e. they should be regarded as having equal opposite utility.