One thing that should be noted is that while Adam's argument is influential, especially since it first (to my knowledge) pointed out halfers have to either reject Bayesian updating upon learning it is Monday or accept a fair coin yet to be tossed has the probability other than 1/2. Thirders in general disagree with it in some crucial ways. Most notably Adam argued that there is no new information when waking up in the experiment. In contrast, most thirders endorsing some versions of SIA would say waking up in the experiment is evidence favouring Tails, which has more awakenings. Therefore targeting Adam's argument specifically is not very effective.
In your incubator experiment, thirders, in general, would find no problem: waking up, evidence favouring tails P(T)=2/3. Finding it is room 1: evidence favouring Heads, P(T) decreased to 1/2.
Here is a model that might interest halfers. You participate in this experiment: the experimenter tosses a fair coin, if Heads nothing happens, you sleep through the night uneventfully. If Tails they will split you in the middle into two halves, completing each half by cloning the missing part onto it. The procedure is accurate enough that the memory is preserved in both copies. Imagine yourself waking up the next morning: you can't tell if anything happened to you, if either of your halves is the same physical piece yesterday, or if there is another physical copy in another room. But regardless, you can participate in the same experiment again. The same thing happens when you find yourself waking up the next day. and so on.....As this continues, you will count about an equal number of Heads and Tails in the experiments you have subjective experiences of...
Counting subjective experience does not necessarily lead to Thirderism.
Thirders in general disagree with it in some crucial ways. Most notably Adam argued that there is no new information when waking up in the experiment. In contrast, most thirders endorsing some versions of SIA would say waking up in the experiment is evidence favouring Tails, which has more awakenings. Therefore targeting Adam's argument specifically is not very effective.
I think there is a weird knot of contradictions hidden there. On one hand, Elga's mathematical model doesn't include anything about awakening. But then people rationalize that the update on awakening is the justification why according to this model the probability of a fair coin landing Tails is always 2/3, instead of noticing that the model just returns contradictory results.
In your incubator experiment, thirders, in general, would find no problem: waking up, evidence favouring tails P(T)=2/3. Finding it is room 1: evidence favouring Heads, P(T) decreased to 1/2.
Which would be a mistake (unless we once again shifted to anthropical motte) because knowing that you are in Room 1 should update you to 2/3 Heads as I've showed here:
coin_guess = []
for n in range(100000):
room, coin = incubator()
beauty_knows_room1 = (room == 1)
if beauty_knows_room1:
coin_guess.append(coin == 'Heads')
print(coin_guess.count(True)/len(coin_guess)) # 0.6688515435956072It's quite curious that "updating on existence" here is equal to not updating on actual evidence. A Thirder who figured out that they are in Room 1 equals to the Halfer who didn't.
To thirders, your simulation is incomplete. It should first include randomly choosing a room and finding it occupied. That will push the probability of Tails to 2/3. Knowing it is room 1 will push it back to 1/2.
Code for incubator function includes random choice of a room on Tails
def incubator(heads_chance=0.5):
if random.random() >= heads_chance: # result of the coin toss
coin = 'Tails'
room = 1 if random.random() >= 0.5 else 2 # room sample
else:
coin = 'Heads'
room = 1
return room, coinThat's not it. In your simulation you give equal chances for Head and Tails, and then subdivide Tails into two equiprobables of T1 and T2 while keeping all probability of Heads as H1. It's essentially a simulation based on SSA. Thirders would say that is the wrong model because it only considers cases where the room is occupied: H2 never appeared in your model. Thirders suggests there is new info when waking up in the experiment because it rejects H2. So the simulation should divide both Head and Tails into equiprobables of H1 H2 T1 T2. And waking up rejects H2 which pushes P(T) to 2/3. And then learning it is room 1 would push it back down to 1/2.
It's essentially a simulation based on SSA.
The other way around. My simulation is based on the experiment as stated. SSA then tries to generalise this principle assuming that all possible experiments are the same - which is clearly wrong.
Thirders position in the incubator-like experiments requires assuming that SBs are randomly sampled, as if God selects a soul from the set of all possible souls and materialise it when a SB is created, and thus thirdism inevitably fails when it's not the case. I'm going to highlight it in the next post which is exploring multiple similar but a bit different scenarios.
My simulation is based on the experiment as stated.
No.
Your simulations for the regular sleeping beauty problem are good, they acknowledge that multiple sleeping beauty awakenings exist in the event of tails and then weight them in different ways according to different philosophical assumptions about how the weighting should occur.
Your simulation for the incubator version on the other hand, does not acknowledge that there are multiple sleeping beauties in the event of tails, and skips directly to sampling between them according to your personal assumptions.
If you were to do it properly, you would find that it is mathematically equivalent to the regular version, with the same sampling/weighting assumptions available each with the same corresponding answers to the regular version.
Note, mathematically equivalent does not mean philosophically equivalent; one could still be halfer for one and thirder for the other; based on which assumptions you prefer in which circumstances, it's just that both halfer and thirder assumptions can exist in both cases and will work equivalently.
Your simulation for the incubator version on the other hand, does not acknowledge that there are multiple sleeping beauties in the event of tails, and skips directly to sampling between them according to your personal assumptions.
The function returns your room an the result of the coin toss. It's enough to determine the existence and if so position of the other Beauty from it. You can also construct thirders scoring rule for the Anthropical Motte without any problem:
coin_guess = []
for n in range(100000):
room, coin = incubator()
coin_guess.append(coin == 'Heads')
if ( coin == Tails ):
coin_guess.append(coin == 'Heads')
print(coin_guess.count(True)/len(coin_guess))In principle I could've added more information on the return for the extra fluff, but the core logic would still be the same.
The incubator code generates a coin toss and a room. If the first coin toss is tails, the room is selected randomly based on a second coin toss, which does not acknowledge that both rooms actually occur in the real experiment, instead baking in your own assumptions about sampling.
Then, your "thirders scoring rule" takes only the first coin toss from the incubator code, throwing out all additional information, to generate a set of observations to be weighted according to thirder assumptions. While this "thirders scoring rule" does correctly reflect thirder assumptions that does not make the original incubator code compatible with thirder assumptions, since all you used from it was the initial coin toss. You could have just written
coin = "Heads" if random.random() >= 0.5 else "Tails"
in place of
room, coin = incubator()
A better version of the incubator code would be to use exactly the same code as for the "classic" version but just substituting "Room 1" for "Monday" and "Room 2" for "Tuesday".
A better version of the incubator code would be to use exactly the same code as for the "classic" version but just substituting "Room 1" for "Monday" and "Room 2" for "Tuesday"
No, absolutely not. Such modelling would destroy all the assymetry between the two experiments which I'm talking about in the post.
In classic the same person experiences both Monday and Tuesday, even if she doesn't remember it later. In the incubator there are two different people. In classic you can toss a coin after the Monday awakening already happened. In incubator you can't do it when the first person is already created. That's why
but
You could have just written
coin = "Heads" if random.random() >= 0.5 else "Tails"
No, I couldn't. I also need to know which room I am in.
Then, your "thirders scoring rule" takes only the first coin toss from the incubator code, throwing out all additional information, to generate a set of observations to be weighted according to thirder assumptions.
Whatever "additional information" thirders assume there is, it's either is represented in the result of the coin toss and which room I am in, or their assumptions are not applicable for the incubator experiment.
Anyway here is a more explicit implementation with both scoring rules. :
def incubator(heads_chance=0.5):
if random.random() >= heads_chance: # result of the coin toss
coin = 'Tails'
my_room = 1 if random.random() >= 0.5 else 2 # room sample
other_room = 2 if my_room == 1 else 1
return {'my_room': my_room, 'other_room': other_room}, coin
else:
coin = 'Heads'
my_room = 1
return {'my_room': my_room}, coin
coin_guess = []
for n in range(100000):
rooms, coin = incubator()
my_room = rooms['my_room']
for room in rooms.values():
if room == my_room:
coin_guess.append(coin == 'Heads')
coin_guess = []
for n in range(100000):
rooms, coin = incubator()
for room in rooms.values():
coin_guess.append(coin == 'Heads')The results are all the same. You in particular has only 50% to guess the result of the coin toss - that's the bailey. But if you also count the other person guesses - construct the thriders scoring rule you together get 2/3 for Tails - that's the motte.
Such modelling would destroy all the assymetry between the two experiments which I'm talking about in the post.
Exactly. There is no asymmetry (mathematically). I agree in principle that one could make different assumptions in each case, but I think making the same assumptions is probably common without any motte/bailey involved and equivalent assumptions produce mathematically equivalent results.
As this is the key point in my view, I'll point out how the classic thirder argument is the same/different for the incubator case and relegate brief comments on your specific arguments to a footnote[1].
Here is the classic thirder case as per Wikipedia:
The thirder position argues that the probability of heads is 1/3. Adam Elga argued for this position originally[2] as follows: Suppose Sleeping Beauty is told and she comes to fully believe that the coin landed tails. By even a highly restricted principle of indifference, given that the coin lands tails, her credence that it is Monday should equal her credence that it is Tuesday, since being in one situation would be subjectively indistinguishable from the other. In other words, P(Monday | Tails) = P(Tuesday | Tails), and thus
P(Tails and Tuesday) = P(Tails and Monday).
Suppose now that Sleeping Beauty is told upon awakening and comes to fully believe that it is Monday. Guided by the objective chance of heads landing being equal to the chance of tails landing, it should hold that P(Tails | Monday) = P(Heads | Monday), and thus
P(Tails and Tuesday) = P(Tails and Monday) = P(Heads and Monday).
Since these three outcomes are exhaustive and exclusive for one trial (and thus their probabilities must add to 1), the probability of each is then 1/3 by the previous two steps in the argument.
Here is the above modified to apply to the incubator version. Most straightforwardly would still apply, but I've bolded the most questionable step:
The thirder position argues that the probability of heads is 1/3. Adam Elga would argue for this position (modified) as follows: Suppose Sleeping Beauty is told and she comes to fully believe that the coin landed tails. By even a highly restricted principle of indifference, given that the coin lands tails, her credence that she is in Room 1 should equal her credence that she is in Room 2 since being in one situation would be subjectively indistinguishable from the other. In other words, P (Room 1 | Tails) = P(Room 2 | Tails), and thus
P(Tails and Room 1) = P(Tails and Room 2).
Suppose now that Sleeping Beauty is told upon awakening and comes to fully believe that she is in Room 1. Guided by the objective chance of heads landing being equal to the chance of tails landing, it should hold that P(Tails | Room 1) = P(Heads | Room 1), and thus
P(Tails and Room 2) = P(Tails and Room 1) = P(Heads and Room 1).
Since these three outcomes are exhaustive and exclusive for one trial (and thus their probabilities must add to 1), the probability of each is then 1/3 by the previous two steps in the argument.
Now, since as you point our you can't make the decision to add Room 2 later in the incubator experiment as actually written, this bolded step is more questionable than in the classic version. However, one can still make the argument, and there is no contradiction with the classic version - no motte/bailey. I note that you could easily modify the incubator version to add Room 2 later. In that case, Elga's argument would apply pretty much equivalently to the classic version. Maybe you think changing the timing to make it simultaneous vs. nonsimultaneous should result in different outcomes - that's fine, your personal opinion - but it's not irrational for a person to think it doesn't make a difference!
- ^
same person/different people - concept exists in map, not territory. Physical continuity/discontinuity on the other hand does exist in territory, but relevance should be argued not assumed; and certainly if one wants to consider someone irrational for discounting the relevance, that would need a lot of justification!
timing of various events - exists in territory, but again relevance should not be assumed, and need justification to consider discounting it as irrational.
but
You claim; but consistent assumptions could be applied to make them equivalent (such as my above modification of Elga's argument still being able to apply equivalently in both cases).
No, I couldn't. I also need to know which room I am in.
You literally just threw away that information (in the "thirders scoring rule" which is where I suggested you could make that replacement)!
Whatever "additional information" thirders assume there is, it's either is represented in the result of the coin toss and which room I am in, or their assumptions are not applicable for the incubator experiment.
Yes, but... you threw away the room information in your "thirders scoring rule"!
Anyway here is a more explicit implementation with both scoring rules. :
That works. Note that your new thirder scoring rule still doesn't care what room "you" are in, so your initial sampling (which bakes in your personal assumptions) is rendered irrelevant. The classic code also works, and in my view correctly represents the incubator situation with days changed to rooms.
You in particular
Another case of: concept exists in map, not territory (unless we are already talking about some particular Sleeping Beauty instance).[2]
- ^
While I'm on the subject of concepts that exist in the map, not the territory, here's another one:
Probability (at least the concept of some particular subjective probability being "rational")
In my view, a claim that some subjective probability is rational amounts to something like claiming that that subjective probability will tend to pay off in some way...which is why I consider it to be ambiguous in Sleeping Beauty since the problem is specifically constructed to avoid any clear payoffs to Sleeping Beauty's beliefs. FWIW though, I do think that modifications that would favour thirderism (such as Radford Neal's example of Sleeping Beauty deciding to leave the room) tend to seem more natural to me personally than modifications that would favour halferism. But that's a judgement call and not enough for me to rule halferism out as irrational.
I've been reading about this problem as well, due to a Manifold Question I made on the topic. So far I found the paper "Bayesian Beauty" the most clear and convincing explanation of the thirder position. Still, I have more to read. Here it is: https://link.springer.com/article/10.1007/s10670-019-00212-4
I'm also influenced by bettors who think that when we do get consensus on the problem, it's more likely to be a thirder consensus than either type of halfer consensus.
One of the points I'm making in this post is that the question of Sleeping Beauty problem is very context sensitive: people go between antropical motte and anthropical bailey without even realising it.
You should explicitly specify whether by "degree of belief for the coin having come up heads" you mean in this experiment or in this awakening. As you can see
coin_guess = []
for n in range(100000):
days, coin = classic()
for d in days:
coin_guess.append(coin == 'Heads')
coin_guess.count(True)/len(coin_guess) # 0.3322852689217815
coin_guess = {}
for i in range(100000):
days, coin = classic()
for d in days:
coin_guess[i] = (coin == 'Heads')
coin_guess = list(coin_guess.values())
coin_guess.count(True)/len(coin_guess) # 0.50167What answer is the correct one solely depends on how we count. And the whole controversy comes from the ambiguity, where people confuse probability that the coin is Heads with probability that the coin is Heads weighted by the number of awakenings you have.
You should also give link to the original paper with Double Halfer position authored by Mikaël Cozic.
As I show here
coin_guess = []
for n in range(100000):
days, coin = classic()
beauty_knows_monday = (days[0] == 'Monday')
if beauty_knows_monday :
coin_guess.append(coin == 'Heads')
print(coin_guess.count(True)/len(coin_guess)) # 0.49958 Halfer approach promoted by by Lewis is incorrect for the classical version of Sleeping Beauty. Double Halfer reasoning is correct when we are talking about probability and not weighted probability.
And the whole controversy comes from the ambiguity, where people confuse probability that the coin is Heads with probability that the coin is Heads weighted by the number of awakenings you have.
I don't think this is confusion. Obviously no one thinks that any outsider's probability should be different from 1/2, it is just that:
You should explicitly specify whether by "degree of belief for the coin having come up heads" you mean in this experiment or in this awakening.
Thirders think that "this awakening" is the correct way to define subjective probability, you think "this experiment" is the correct way to define subjective probability. It is a matter of definitions, and no confusion is necessarily involved.
Thanks, I'm reading the "Imaging and Sleeping Beauty" paper now, I'll add it to Manifold shortly.
Like Simon, I think the best interpretation of the Sleeping Beauty problem is that it's asking about the probability "in the awakening", and there seems to be consensus that the probability "in the experiment" is 1/2. But I plan to defer to expert consensus once it exists.
I don't think there is consensus that this "in the awakening" probability is 1/3. It looks like Bostrom (2006) invokes SSA to say that in a one-shot Sleeping Beauty experiment the probability is 1/2. And Milano (2022) thinks it depends on priors, so that a solipsistic prior gives probability 1/2.
I also don't think this is just a matter of confusion. With respect to the motte and bailey you describe, it looks to me like many thirders hold the bailey position, both in "classic" and "incubator" versions of the problem. So if you claim that the bailey position is wrong, then there is a real dispute in play.
there seems to be consensus that the probability "in the experiment" is 1/2
I also don't think this is just a matter of confusion. With respect to the motte and bailey you describe, it looks to me like many thirders hold the bailey position, both in "classic" and "incubator" versions of the problem.
Well, you see this is preciesly the confusion I'm talking about.
If there are thirders who hold the bailey position: that particiopating in the experiment gives them the ability to correctly guess tails in 2/3 of the experiments, then there can't be a consensus that probability "in the experiment" is 1/2.
The whole "paradox" is that despite the fact that any random awakening are 2/3 likely to happen when the coin landed Tails, the fact that you are awaken doesn't help you guess the outcome of the coin toss in this experiment better than chance. So it's very important to be very precise about what you mean by "credence" or "probability".
So if you claim that the bailey position is wrong, then there is a real dispute in play.
Yep. This is specifically the dispute I want to adress but to be able to do it one has to properly separate the bailey from the motte first. Next post will explore the bailey position in more details and show how it violates conservation of expected evidence.
I'm now unclear exactly what the bailey position is from your perspective. You said in the opening post, regarding the classic Sleeping Beauty problem:
The Bailey is the claim that the coin is actually more likely to be Tails when I participate in the experiment myself. That is, my awakening on Monday or Tuesday gives me evidence that lawfully update me to thinking that the coin landed Tails with 2/3 probability.
From the perspective of the Bayesian Beauty paper, the thirder position is that, given the classic (non-incubator) Sleeping Beauty experiment, with these anthropic priors:
- P(Monday | Heads) = 1/2
- P(Monday | Tails) = 1/2
- P(Heads) = 1/2
Then the following is true:
- P(Heads | Awake) = 1/3
I think this follows from the given assumptions and priors. Do you agree?
One conversion of this into words is that my awakening (Awake=True) gives me evidence that lawfully updates me from, on Sunday, thinking that the coin will equally land either way (P(Heads) = 1/2) to waking up and thinking that the coin right now is more likely to be showing tails (P(Heads | Awake) = 1/3). Do you disagree with the conversion of the math into words? Would you perhaps phrase it differently?
Whereas now you define the bailey position as:
The bailey position: that participating in the experiment gives them the ability to correctly guess tails in 2/3 of the experiments.
I agree with you that this is false, but it reads to me as a different position.
The Bailey is the claim that the coin is actually more likely to be Tails when I participate in the experiment myself. That is, my awakening on Monday or Tuesday gives me evidence that lawfully update me to thinking that the coin landed Tails with 2/3 probability.
The bailey position: that participating in the experiment gives them the ability to correctly guess tails in 2/3 of the experiments.
Could you explain what is the difference you see between these two position?
If you receive some evidence that lawfully updates you to believing that the coin is Tails with 2/3 probability in this experiment, in 2 out of 3 experiments the coin have to be Tails when you receive this evidence.
If you receive this evidence every experiment you participate in, then the coin have to be Tails 2 out of 3 times when you participate in the experiment and thus you have to be able to correctly guess Tails in 2 out of 3 of experiments.
- P(Monday | Heads) = 1/2
- P(Monday | Tails) = 1/2
- P(Heads) = 1/2
Then the following is true:
- P(Heads | Awake) = 1/3
I think this follows from the given assumptions and priors. Do you agree?
There is a fundamental issue with trying to apply formal probability theory to the classic Sleeping Beauty, because the setting doesn't satisfy the assumptions of Kolmogorov axioms. P(Monday) and P(Tuesday) are poorly defined and are not actually two elementary outcomes necessary for solution space because Tuesday follows Monday. Likewise, P(Heads&Monday), P(Tails&Monday) and P(Tails&Tuesday) are poorly defined and are not three elementary outcomes for the similar reason.
I'll give a deeper read to the Bayesian Beauty paper, but from what I've already seen it just keeps uplying the same mathematical apparatus to the setting that it's not properly fitting.
Could you explain what is the difference you see between these two position?
In the second one you specifically describe "the ability to correctly guess tails in 2/3 of the experiments", whereas in the first you more loosely describe "thinking that the coin landed Tails with 2/3 probability", which I previously read as being a probability per-awakening rather than per-coin-flip.
Would it be less misleading if I change the first phrase like this:
The Bailey is the claim that the coin is actually more likely to be Tails when I participate in the experiment myself. That is, my awakening on Monday or Tuesday gives me evidence that lawfully update me to thinking that the coin landed Tails with 2/3 probability in this experiment, not just on average awakening.
Thank you for sharing that Bayesian Beauty paper, its very clear.
I think the OP is onto something useful when they distinguish between (my phrasing) the approach such that "my probabilities are calibrated such that they represent the proportion of timelines in which I am right" and the approach that means "my probabilities are calibrated with respect to the number of times I answer questions about them".
I take the "timelines" (first) option. The second one seems odd to me, for example say someone considers a multiple choice question, decides that answer (a) is correct. They are told they have to wait in the examination room while other candidates finish. During this 10 minute wait they spend 9 minutes confident (a) was the right choice, then with 1 minute to go, realise (b) is actually right and change their answer. Here I would only judge the correctness (or otherwise) of the final choice, (b), and it would not be relevant that they spent more time believing (a). Similarly, if Beauty is woken for a second time any guesses she makes about the coin on this second waking should be taken to replace any guesses she made on the first waking (if you take the timelines point of view). I think we should only mark "final answers", otherwise we end up in really weird territory where if you think something is true with 2/3rds probability, but you used to think it was true with 1/3rd probability, then you should exaggerate your newfound belief that it is more likely in order to be more right on a temporal average.
Argument against marking only final answers: on Wednesday Beauty wakes up, and learns that the experiment has concluded. At this time her credence for P(heads) is 1/2. This is true both on a per-Wednesday-awakening basis and on a per-coin-flip basis, regardless of whether she is a thirder, halfer, or something else. If we only mark final answers, the question of the correct probability on Monday and Tuesday is left with no answer.
I agree that you can make a betting/scoring setup such that betting/predicting at 50% is correct. Eg, suppose that on both Monday and Tuesday, Beauty gets to make a $1 bet at some odds. If she's asleep on Tuesday then whatever bet she made on Monday is repeated. In that case she should bet at 1:1 odds. With other scoring setups we can get different answers. Overall, this makes me think that this approach is misguided, unless we have a convincing argument about which scoring setup is correct.
I think the exam hypothetical creates misleading intuitions because written exams are generally graded based on the final result. Whereas if this was an oral examination in spoken language, a candidate who spent the first nine minutes with incorrect beliefs about grammatical gender would lose points. But certainly if I knew my life was being scored based on my probabilities at the moment of death, I would optimize for dying in a place of accurate certainty.
Yes, the Wednesday point is a good one, so it the oral exam comparison.
I think we agree that the details of the "scoring system" completely change the approach beauty should take. This is not true for most probability questions. Like, if she can bet 1$ at some odds each time she wakes up then it makes sense for her policy going in to more heavily weight the timeline in which she gets to bet twice. As you point out if her sleeping self repeats bets that changes things. If the Tuesday bet is considered to be "you can take the bet, but it will replace the one you may or may not have given on a previous day if their was one", then things line up to half again. If she has to guess the correct outcome of the coin flip, or else die once the experiment is over, then the strategy where she always guesses heads is just as good as the one where she always guesses tails. Her possible submissions are [H, T, HH, TT], two of which result in death. Where we differ is that you think the details of the scoring system being relevant suggest the approach is misguided. In contrast I think the fact that scoring system details matter is the entire heart of the problem. If I take probabilities as "how I should bet" then the details of the bet should matter. If I take probabilities as frequencies then I need to decide whether the denominator is "per timeline" or "per guess". I don't think the situation allows one to avoid these choices, and (at least to me) once these are identified as choices, with neither option pushed upon us by probability theory, the whole situation appears to make sense.
Frequentist example --- If you understood me above you certainly don't need this example so skip ---: The experiment is repeated 100 times, with 50 heads and 50 tails on the coin flip. A total of 150 guesses are made by beauty. BeautyV1.0 said the probability was 50/50 every time. This means that for 100 of the times she answered 50/50 it was actually tails, and 50 times she answered this same way it was actually heads. So she is poorly calibrated with respect to the number of times she answered. By this scoring system BeautyV2.0 who says "1/3" appears better.
However, in every single trial, even the ones where beauty is consulted twice, she only provides one unique answer. If beauty is a simple program call in a simulation then she is a memoryless program, in some cases evaluated twice. In half the trials it was heads, in half it was tails, in every trial BeautyV1.0 said it was 50/50. So she is well calibrated per trial, but not per evaluation. BeautyV2.0 is the other way around.
the details of the "scoring system" completely change the approach beauty should take. This is not true for most probability questions.
I believe this IS true for most probability questions. However, most probability questions have only one reasonable scoring system to consider, so you don't notice the question.
If the Tuesday bet is considered to be "you can take the bet, but it will replace the one you may or may not have given on a previous day if their was one", then things line up to half again.
I can think of two interpretations of the setup you're describing here, but for both interpretations, Beauty does the right thing only if she thinks Heads has probability 1/3, not 1/2.
Note that depending on the context, a probability of 1/2 for something does not necessarily lead one to bet on it at 1:1 odds. For instance, if based on almost no knowledge of baseball, you were to assign probability 1/2 to the Yankees winning their next game, it would be imprudent to offer to bet anyone that they will win, at 1:1 odds. It's likely that the only people to take you up on this bet are the ones who have better knowledge, that leads them to think that the Yankees will not win. But even after having decided not to offer this bet, you should still think the probability of the Yankees winning is 1/2, assuming you have not obtained any new information.
I'll assume that Beauty is always given the option of betting on Heads at 1:1 odds. From an outside view, it is clear that whatever she does, her expected gain is zero, so we hope that that is also her conclusion when analyzing the situation after each awakening. Of course, by shifting the payoffs when betting on Heads a bit (eg, win $0.90, lose $1) we can make betting on Heads either clearly desirable or clearly undesirable, and we'd hope that Beauty correctly decides in such cases.
So... first interpretation: At each awakening, Beauty can bet on Heads at 1:1 odds (winning $1 or losing $1), or decide not to bet. If she decides to bet on Tuesday, any bet she may have made on Monday is cancelled, and if she decides not to bet on Tuesday, any bet she made on Monday is also cancelled. In other words, what she does on Monday is irrelevant if the coin landed Tails, since she will in that case be woken on Tuesday and whatever she decides then will replace whatever decision she made on Monday. (Of course, if the coin landed Heads, her decision on Monday does take effect, since she isn't woken on Tuesday.)
Beauty's computation on awakening of the expected gain from betting on Heads (winning $1 or losing $1) can be written as follows:
P(Heads&Monday)*1 + P(Tails&Monday)*0 + P(Tails&Tuesday)*(-1)
The 0 gain from betting on Monday when the coin landed Tails is because in that situation her decision is irrelevant. The expected gain from not betting is of course zero.
If Beauty thinks that P(Heads)=1/3, and hence P(Heads&Monday)=1/3, P(Tails&Monday)=1/3, and P(Tails&Tuesday)=1/3, and the formula above evaluates to zero, as we would hope. Furthermore, if the payoffs deviate from 1:1, Beauty will decide to bet or not in the correct way.
If Beauty instead thinks that P(Heads)=1/2, then P(Heads&Monday)=1/2. Trying to guess what a Halfer would think, I'll also assume that she thinks that P(Tails&Monday)=1/4 and P(Tails&Tuesday)=1/4. (Those who deny that these probabilities should sum to one, or maintain that the concept of probability is inapplicable to Beauty's situation, are beyond the bounds of rational discussion.) If we plug these into the formula above, we get that Beauty thinks her expected gain from betting on Heads is $0.25, which is contrary to the outside view that it is zero. Furthermore, if we shift the payoffs a little bit, so a win betting on Heads gives $0.90 and a loss betting on Heads still costs $1, then Beauty will compute the expected gain from betting on Heads to be $0.45 minus $0.25, which is $0.20$, so she's still enthusiastic about betting on Heads. But the outside view is that with these payoffs the expected gain is minus $0.05, so betting on Heads is a losing proposition.
Now... second interpretation: At each awakening, Beauty can bet or decide not to bet. If she decides to bet on Tuesday, any bet she may have made on Monday is cancelled, but if she decides not to bet on Tuesday, a bet she made on Monday is still in effect. In other words, she makes a bet if she decides to bet on either Monday or Tuesday, but if she decides to bet on both Monday and Tuesday, it only counts as one bet.
This one is more subtle. I answered essentially the same question in a comment on this blog post, so I'll just copy the relevant portion below, showing how a Thirder will do the right thing (with other than 1:1 payoffs). Note that "invest" means essentially the same as "bet":
- - -
First, to find the optimal strategy in this situation where investing when Heads yields -60 for Beauty, and investing when Tails yields +40 for Beauty, but only once if Beauty decides to invest on both wakenings, we need to consider random strategies in which with probability q, Beauty does not invest, and with probability (1-q) she does invest.
Beauty’s expected gain if she follows such a strategy is (1/2)40(1-q^2)-(1/2)60(1-q). Taking the derivative, we get -40q+30, and solving for this being zero gives q=3/4 as the optimal value. So Beauty should invest with probability 1/4, which works out to giving her an average return of (1/2)40(7/16)-(1/2)60(1/4)=5/4.
That’s all when working out the strategy beforehand. But what if Beauty re-thinks her strategy when she is woken? Will she change her mind, making this strategy inconsistent?
Well, she will think that with probability 1/3, the coin landed Heads, and the investment will lose 60, and with probability 2/3, the coin landed Tails, in which case the investment will gain 40, but only if she didn’t/doesn’t invest in her other wakening. If she follows the strategy worked out above, in her other wakening, she doesn’t invest with probability 3/4, and if Beauty thinks things over with that assumption, she will see her expected gain as (2/3)(3/4)40-(1/3)60=0. With a zero expected gain, Beauty would seem indifferent to investing or not investing, and so has no reason to depart from the randomized strategy worked out beforehand. We might hope that this reasoning would lead to a positive recommendation to randomize, not just acquiescence to doing that, but in Bayesian decision theory randomization is never required, so if there’s a problem here it’s with Bayesian decision theory, not with the Sleeping Beauty problem in particular.
- - -
On the other hand, if Beauty thinks the probability of Heads is 1/2, then she will think that investing has expected return of (1/2)(-60) + (1/2)40 or less (the 40 assumes she didn't/doesn't invest on the other awakening, if she did/does it would be 0). Since this is negative, she will change her mind and not invest, which is a mistake.
"If Beauty instead thinks that P(Heads)=1/2, then P(Heads&Monday)=1/2. Trying to guess what a Halfer would think, I'll also assume that she thinks that P(Tails&Monday)=1/4 and P(Tails&Tuesday)=1/4"
This part of the analysis gets to the core of my opinion. One could argue that if the coin is flicked and comes up tails then we have both "Tails&Monday" and "Tails&Tuesday" as both being correct, sequentially. They are not mutually exclusive outcomes. One could also argue that, on a particular waking up Beauty doesn't know which day it is and thus they are exclusive in that moment.*
Which gets me back to my point. What do you mean by "probability". If we take a frequentist picture do we divide by the number of timelines (or equivalently separate experimental runs if many are run), or do we divide by the number of times beauty wakes up. I think either can be defended and that you should avoid the words "probability" or the notation P( X ) until after you have specified which denominator you are taking.
I like the idea of trying to evaluate the optimal policy for Beauty, given the rules of the game. Maybe you are asked to right a computer function (Beauty.py) that is going to play the game as described.
I liked the thought about indeteriminisitc strategies sometimes being the best. I cooked up an extreme example underneath here to (1) show how I think the "find the optimal policy approach" works in practice and to (2) give another example of randomness being a real friend.
Consider two very extreme cases of the sleeping beauty game:
Guess wrong and you die! (GWYD)
Guess right and you live! (GRYL)
In both instances beauty guesses whether the coin was heads of tails on each waking. After the experiment is over her guesses are considered. In the first game, one (or more) wrong guesses get beauty killed. In the Second a single right guess is needed, otherwise she is killed.
In the first game, GWYD, (I think) it is obvious that the deterministic strategy "guess heads" is just as good as the deterministic strategy "guess tails". Importantly the fact that Beauty is sometimes woken twice is just not relevant in this game: because providing the same answer twice (once on each day) changes nothing. As both the "guess tails" and "guess heads" policies are considered equally good one could say that the revealed probability of heads is 1/2. (Although as I said previously I would avoid the word "probability" entirely and just talk about optimal strategies given some particular scoring system).
However, in the second game, GRYL, it is clear that a randomised strategy is best (assuming beauty has access to a random number generator). If the coin does come up tails then Beauty gets two guesses and (in GRYL) it would be very valuable for those two guesses to be different from one another. However, if it is heads she gets only one try.
I drew myself a little tree diagram expecting to find that in GRYL the probabilities revealed by the optimal policy would be thirder ones, but I actually found that the optimal strategy in this case is to guess heads with 50% probability, and tails with 50% probability (overall giving a survival chance of 5/8).
I had vaguely assumed that GWYD was a "halfers game" and GRYL was a "thirders". Odd that they both give strategies that feel "halfer-y". (It remains the case that in a game where right guesses are worth +1$ and wrong guesses -1$ that the thirder tactic is best, guess tails every time, expect to win 2/3rds).
* One could go even crazier and argue that experiences that are, by definition (amnesia drug) indistinguishable should be treated like indistinguishable particles.
One could argue that if the coin is flicked and comes up tails then we have both "Tails&Monday" and "Tails&Tuesday" as both being correct, sequentially.
Yes, it is a commonplace occurrence that "Today is Monday" and "Today is Tuesday" can both be true, on different days. This doesn't ordinarily prevent people from assigning probabilities to statements like "Today is Monday", when they happen to not remember for sure whether it is Monday or not now. And the situation is the same for Beauty - it is either Monday or Tuesday, she doesn't know which, but she could find out if she just left the room and asked some passerby. Whether it is Monday or Tuesday is an aspect of the external world, which one normally regards as objectively existing regardless of one's knowledge of it.
All this is painfully obvious. I think it's not obvious to you because you don't accept that Beauty is a human being, not a python program. Note also that Beauty's experience on Monday is not the same as on Tuesday (if she is woken). Actual human beings don't have exactly the same experiences on two different days, even if the have memory issues. The problem setup specifies only that these differences aren't informative about whether it's Monday or Tuesday.
What do you mean by "probability".
I'm using "probability" in the subjective Bayesian sense of "degree of belief". Since the question in the Sleeping Beauty problem is what probability of Heads should Beauty have when awoken, I can't see how any other interpretation would address the question asked. Note that these subjective degree-of-belief probabilities are intended to be a useful guide to decision-making. If they lead one to make clearly bad decisions, they must be wrong.
Consider two very extreme cases of the sleeping beauty game: - Guess wrong and you die! (GWYD) - Guess right and you live! (GRYL)
If we look at the GWYD and GRYL scenarios you describe, we can, using an "outside" view, see what the optimal strategies are, based on how frequently Beauty survives in repeated instances of the problem. To see whether Beauty's subjective probability of Heads should be 1/2 or 1/3, we can ask whether after working out an optimal strategy beforehand, Beauty will change her mind after waking up and judging that P(Heads) is either 1/2 or 1/3, and then using that to decide whether to follow the original strategy or not. If Beauty's judgement of P(Heads) leads to her abandoning the optimal strategy, there must be something wrong with that P(Heads).
For GWYD, both the strategy of deterministically guessing Heads on all awakenings and the strategy of deterministically guessing Tails on all awakenings will give a survival probability of 1/2, which is optimal (I'll omit the proof of this).
Suppose Beauty decides ahead of time to deterministically guess Tails. Will she change her mind and guess Heads instead when she wakes up?
Suppose that Beauty thinks that P(Heads)=1/3 upon wakening. She will then think that if she guesses Heads, her probability of surviving is P(Heads)=1/3. If instead, she guesses Tails, she thinks her probability of surviving is P(Tails & on other wakening she also guesses Tails), which is 2/3 if she is sure to follow the original plan in her other wakening, and is greater than 1/3 as long as she's more likely than not to follow the original plan on her other wakening. So unless Beauty thinks she will do something perverse on her other wakening, she should think that following the original plan and guessing Tails is her best action.
Now suppose that Beauty thinks that P(Heads)=1/2 upon wakening. She will then think that if she guesses Heads, her probability of surviving is P(Heads)=1/2. If instead, she guesses Tails, she thinks her probability of surviving is P(Tails & on other wakening she also guesses Tails), which is 1/2 if she is sure to follow the original plan in her other wakening, and less than 1/2 if there is any chance that on her other wakening she doesn't follow the original plan. Since Beauty is a human being, who at least once in a while does something strange or mistaken, the probability that she won't follow the plan on her other wakening is surely not zero, so Beauty will judge her survival probability to be greater if she guesses Heads than if she guesses Tails, and abandon the original plan of guessing Tails.
Now, if Beauty thinks P(Heads)=1/2 and then always reasons in this way on wakening, then things turn out OK - despite having originally planned to always guess Tails, she actually always guesses Heads. But if there is a non-negligible chance that she follows the original plan without thinking much, she will end up dead more than half the time.
So if Beauty thinks P(Heads)=1/3, she does the right thing, but if Beauty thinks P(Heads)=1/2, she maybe does the right thing, but not really reliably.
Turning now to the GRYL scenario, we need to consider randomized strategies. Taking an outside view, suppose that Beauty follows the strategy of guessing heads with probability h, independently each time she wakes. Then the probability that she survives is S=(1/2)h+(1/2)(1-h*h) - that is, the probability the coin lands Heads (1/2) times the probability she guesses Heads, plus the probability that the coin lands Tails time the probability that she doesn't guess Heads on both awakenings. The derivative of S with respect to h is (1/2)-h, which is zero when h=1/2, and one can verify this gives a maximum for S of 5/8 (better than the survival probability when deterministically guessing either Heads of Tails).
This matches what you concluded. However, Beauty guessing Heads with probability 1/2 does not imply that Beauty thinks P(Heads)=1/2. The "guess" here is not made in an attempt to guess the coin flip correctly, but rather in an attempt to not die. The mechanism for how the guess influences whether Beauty dies is crucial.
We can see this by seeing what Beauty will do after waking if she thinks that P(Heads)=1/2. She knows that her original strategy is to randomly guess, with Heads and Tails both having probability 1/2. But she can change her mind if this seems advisable. She will think that if she guesses Tails, her probability of survival will be P(Tails)=1/2 (she won't survive if the coin landed Heads, because this will be her only (wrong) guess, and she will definitely survive if the coin landed Tails, regardless what she does on her other awakening). She will also compute that if she guesses Heads, she will survive with probability P(Heads)+P(Tails & she guesses Tails on her other wakening). Since P(Heads)=1/2, this will be greater than 1/2, since the second term surely is not exactly zero (it will be 1/4 if she follows the original strategy on her other awakening). So she will think that guessing Heads gives her a strictly greater chance of surviving than guessing Tails, and so will just guess Heads rather than following the original plan of guessing randomly.
The end result, if she reasons this way each awakening, is that she always guesses Heads, and hence survives with probability 1/2 rather than 5/8.
Now lets see what Beauty does if after wakening she thinks that P(Heads)=1/3. She will think that if she guesses Tails, her probability of survival will be P(Tails)=2/3. She will think that if she guesses Heads, her probability of survival will be P(Heads)+P(Tails & she guesses Tails on her other wakening). If she thinks she will follow the original strategy on her other wakening, the this is (1/3)+(2/3)*(1/2)=2/3. Since she computes her probability of survival to be the same whether she guesses Heads or Tails, she has no reason to depart from the original strategy of guessing Heads or Tails randomly. (And this reinforces her assumption that on another wakening she would follow the original strategy.)
So if Beauty is a Thirder, she lives with probability 5/8, but if she is a Halfer, she lives with lower probability of 1/2.
We are in complete agreement about how beauty should strategize given each of the three games (bet a dollar on the coin flick with odds K, GWYL and GWYD). The only difference is that you are insisting that "1/3" is Beauty's "degree of belief". (By the way I am glad you repeated the same maths I did for GWYD, it was simple enough but the answer felt surprising so I am glad you got the same.)
In contrast, I think we actually have two quantities:
"Quobability" - The frequency of correct guesses made divided by the total number of guesses made.
"Srobability" - The frequency of trials in which the correct guess was made, divided by the number of trials.
Quabability is 1/3, Scrobability is 1/2. "Probability" is (I think) an under-precise term that could mean either of the two.
You say you are a Bayesian, not a frequentist. So for you "probability" is degree of belief. I would also consider myself a Bayesian, and I would say that normally I can express my degree of belief with a single number, but that in this case I want to give two numbers, "Quobability = 1/3, Scrobability =1/2". What I like about giving two numbers is that typically a Bayesian's single probability value given is indicative of how they would bet. In this case the two quantities are both needed to see how I would bet given slightly varies betting rules.
I was still interested in "GRYL", which I had originally assumed would support the thirder position, but (for a normal coin) had the optimal tactic being to pick at 50/50 odds. I just looked at biased coins.
For a biased coin that (when flicked normally, without any sleep or anmesia) comes up heads with probability k. (k on x-axis), I assume Beauty is playing GRYL, and that she is guessing heads with some probability. The optimal probability for her strategy to take is on the y-axis (blue line). Overall chance of survival is orange line.
You are completely correct that her guess is in no way related to the actual coin bias (k), except for k=0.5 specifically which is an exception not the rule. In fact, this graph appears to be vaguely pushing in some kind of thirder position, in that the value 2/3rds takes on special significance as beyond this point beauty always guesses heads. In contrast when tails is more likely she still keeps some chance of guessing heads because she is banking on one of her two tries coming up tails in the case of tails, so she can afford some preparation for heads.
CODE
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
def p_of_k(k):
if k==1:
return 1
nominal_p = -1 * k / (2 *(k-1))
if nominal_p > 1:
return 1
elif nominal_p < 0:
return 0
else:
return nominal_p
p_live = lambda k, p: k*p + (1-k) *(1-p**2)
ks = np.linspace(0, 1, 100)
dat = []
lives = []
for k in ks:
dat.append( p_of_k(k) )
lives.append( p_live(k, dat[-1] ) )
fig, ax = plt.subplots(figsize=(5,5))
ax.plot( ks, dat )
ax.plot( ks, lives)
ax.annotate("2/3", (0.6666, 1))
ax.grid()
ax.set_xticks(np.linspace(0, 1, 5))
ax.set_yticks(np.linspace(0, 1, 5))
I think we actually have two quantities:
"Quobability" - The frequency of correct guesses made divided by the total number of guesses made.
"Srobability" - The frequency of trials in which the correct guess was made, divided by the number of trials.
Quabability is 1/3, Scrobability is 1/2. "Probability" is (I think) an under-precise term that could mean either of the two.
I suspect that the real problem isn't with the word "probability", but rather the word "guess". In everyday usage, we use "guess" when the aim is to guess correctly. But the aim here is to not die.
Suppose we rephrase the GRYL scenario to say that Beauty at each awakening takes one of two actions - "action H" or "action T". If the coin lands Heads, and Beauty takes action H the one time she is woken, then she lives (if she instead takes action T, she dies). If the coin lands Tails, and Beauty takes action T at least one of the two times she is woken, then she lives (if she takes action H both times, she dies).
Having eliminated the word "guess", why would one think that Beauty's use of the strategy of randomly taking action H or action T with equal probabilities implies that she must have P(Heads)=1/2? As I've shown above, that strategy is actually only compatible with her belief being that P(Heads)=1/3.
Note that in general, the "action space" for a decision theory problem need not be the same as the "state space". One might, for example, have some uncertain information about what day of the week it is (7 possibilities) and on that basis decide whether to order pepperoni, anchovy, or ham pizza (3 possibilities). (You know that different people, with different skills, usually make the pizza on different days.) So if for some reason you randomized your choice of action, it would certainly not say anything directly about your probabilities for the different days of the week.
Maybe we are starting to go in circles. But while I agree the word "guess" might be problematic I think you still have an ambiguity with what the word probability means in this case. Perhaps you could give the definition you would use for the word "probability".
"In everyday usage, we use "guess" when the aim is to guess correctly." Guess correctly in the largest proportion of trials, or in the largest proportion of guesses? I think my "scrob" and "quob" thingies are indeed aiming to guess correctly. One in the most possible trials, the other in the most possible individual instances of making a guess.
"Having eliminated the word "guess", why would one think that Beauty's use of the strategy of randomly taking action H or action T with equal probabilities implies that she must have P(Heads)=1/2?" - I initially conjectured this as weak evidence, but no longer hold the position at all, as I explained in the post with the graph. However, I still think that in the other death-scenario (Guess Wrong you die) the fact that deterministically picking heads is equally good to deterministically picking tails says something. This GWYD case sets the rules of the wager such that Beauty is trying to be right in as many trials as possible, instead of for as many individual awakenings. Clearly moving the goalposts to the "number of trials" denominator.
For me, the issue is that you appear to take "probability" as "obviously" meaning "proportion of awakenings". I do not think this is forced on us by anything, and that both denominators (awakenings and trials) provide us with useful information that can beneficially inform our decision making, depending on whether we want to be right in as many awakenings or trials as possible. Perhaps you could explain your position while tabooing the word "probability"? Because, I think we have entered the Tree-falling-in-forest zone: https://www.lesswrong.com/posts/7X2j8HAkWdmMoS8PE/disputing-definitions, and I have tried to split our problem term in two (Quobability and Srobability) but it hasn't helped.
Perhaps you could give the definition you would use for the word "probability".
I define it as one's personal degree of belief in a proposition, at the time the judgement of probability is being made. It has meaning only in so far it is (or may be) used to make a decision, or is part of a general world model that is itself meaningful. (For example, we might assign a probability to Jupiter having a solid core, even though that makes no difference to anything we plan to do, because that proposition is part of an overall theory of physics that is meaningful.)
Frequentist ideas about probability being related to the proportion of times that an event occurs in repetitions of a scenario are not part of this definition, so the question of what denominator to use does not arise. (Looking at frequentist concepts can sometimes be a useful sanity check on whether probability judgements make sense, but if there's some conflict between frequentist and Bayesian results, the solution is to re-examine the Bayesian results, to see if you made a mistake, or to understand why the frequentist results don't actually contradict the Bayesian result.)
If you make the right probability judgements, you are supposed to make the right decision, if you correctly apply decision theory. And Beauty does make the right decision in all the Sleeping Beauty scenarios if she judges that P(Heads)=1/3 when woken before Wednesday. She doesn't make the right decision if she judges that P(Heads)=1/2. I emphasize that this is so for all the scenarios. Beauty doesn't have to ask herself, "what denominator should I be using?". P(Heads)=1/3 gives the right answer every time.
Another very useful property of probability judgements is that they can be used for multiple decisions, without change. Suppose, for example, that in the GWYD or GRYL scenarios, in addition to trying not to die, Beauty is also interested in muffins.
Specifically, she knows from the start that whenever she wakes up there will be a plate of freshly-baked muffins on her side table, purchased from the cafe down the road. She knows this cafe well, and in particular knows that (a) their muffins are always very delicious, and (b) on Tuesdays, but not Mondays, the person who bakes the muffins adds an ingredient that gives her a stomach ache 10 minutes after eating a muffin. Balancing these utilities, she decides to eat the muffins if the probability of it being Tuesday is less than 30%. If Beauty is a Thirder, she will judge the probability of Tuesday to be 1/3, and refrain from eating the muffins, but if Beauty is a Halfer, she will (I think, trying to pretend I'm a halfer) think the probability of Tuesday is 1/4, and eat the muffins.
The point here is not so much which decision is correct (though of course I think the Thirder decision is right), but that whatever the right decision is, it shouldn't depend on whether Beauty is in the GWYD or GRYL scenario. She shouldn't be considering "denominators".
I agree that you can make a betting/scoring setup such that betting/predicting at 50% is correct. Eg,suppose that on both Monday and Tuesday, Beauty gets to make a $1 bet at some odds. If she's asleep on Tuesday then whatever bet she made on Monday is repeated. In that case she should bet at 1:1 odds.
Let's work it out if Beauty has 1/3 probability for Heads, with the 2/3 probability for Tails split evenly between 1/3 for Tails&Monday and 1/3 for Tails&Tuesday.
Here, the possible actions are "don't bet" or "bet on Heads", at 1:1 odds (let's say win $1 or lose $1), on each day for which a bet is active.
The expected gain from not betting is of course zero. The expected gain from betting on some day can be computed by summing the gains in each situation (Heads&Monday, Tails&Monday, Tails&Tuesday) times the corresponding probabilities:
P(Heads&Monday) x 2 + P(Tails&Monday) x (-1) + P(Tails&Tuesday) x (-1)
This evaluates to zero. Note that the gain for betting in the Heads&Monday situation is $2 because if she makes this bet, it is active for two days, on each of which it wins $1. Since the expected gain is zero for both betting and not betting, Beauty is indifferent to betting on Heads or not betting. If the odds shifted a bit, so winning the bet paid $1 but losing the bet cost $1.06, then the expected gain would be minus $0.04, and Beauty should not make the bet on Heads.
Note that when Beauty is woken on both Monday and Tuesday, we expect that she will make the same decision both days, since she has no reason to make different decisions, but this is not some sort of logical guarantee - Beauty is a human being, who makes decisions for herself at each moment in time, which can conceivably (but perhaps with very low probability) be inconsistent with other decisions she makes at other times.
Now suppose that Beauty's probability for Heads is 1/2, so that P(Heads&Monday)=1/2, P(Tails&Monday)=1/4, and P(Tails&Tuesday)=1/4, though the split between Tails&Monday and Tails&Tuesday doesn't actually matter in this scenario.
Plugging these probabilities into the formula above, we compute the expected gain to be $0.50. So Beauty is not indifferent, but instead will definitely want to bet on Heads. If we shift the payoffs to win $1 lose $1.06, then the expected gain is $0.47, so Beauty will still want to bet on Heads.
However, when a win pays $1 and a loss costs $1.06, arguments from an outside perspective say that if every day she is woken Beauty follows this strategy of betting on Heads, her expected gain is minus $0.03 per experiment. [Edit: Correction, the expected gain per experiment is minus $0.06 - I forgot to multiply by two for the bet being made twice.]
So we see that Beauty makes a mistake if her probability for Heads is 1/2. She makes the right decision (if she applies standard decision theory) if her probability of Heads is 1/3.
Note that this is about how much money Beauty gets. One can get the right answer by applying standard decision theory. There is no role for some arbitrary "scoring setup".
you can't lawfully use probability theory in this setting assuming that Tails and Monday, Tails and Tuesday and Heads and Monday are three exhaustive and exclusive outcomes which probabilities are supposed to be added to 1
Why not?
Suppose for simplicity that Beauty knows that the coin is flipped on Sunday, on a table in a room next to her bedroom, and that the flipped coin is left on the table, with either Heads or Tails showing.
Now, suppose Beauty wakes up (and knows it's not Wednesday, since otherwise she would have been told immediately that it was Wednesday). Although she had been intending go along with this silly experiment, a chance (and unlikely) recollection of something her aunt said to her years ago changes her mind - she decides she has better things to do with her life. She gets up, goes into the next room and sees how the coin landed, and then goes outside and finds out whether it is Monday or Tuesday.
She will discover that the situation is either (Tails, Monday), or (Tails, Tuesday), or (Heads, Monday). Assuming the experimenters behave according to the design of the experiment, one and only one of these will be true. So before she does this, her probabilities for these three events should sum to one.
All that needs to be assumed to reach this conclusion is the common-sense notion of the reality of the external world - that, for example, it is either Monday or not, regardless of whether you happen to know whether it is Monday or not.
This is still a misleading framing, confusing "what she will discover" with "what is (aka: what she is guaranteed to discover later)". (tails, monday), (tails, tuesday), and (heads, monday) are the only experiences she will have, but (heads, tuesday) is assumed to happen in her model of the universe, though she won't know it happened until she's woken on Wednesday.
(Heads, Tuesday) does not occur in conjunction with her waking up, assuming the experimenters behave in the way they say they will. So when she wakes up, it is not a possibility for what her current situation is. Which is what we're talking about.
You don't contradict the claim "you can't lawfully use probability theory in this setting" by showing that you will be able to use probability theory if you break the setting up.
Also if the Beauty changes her mind an decides to break the setting of the experiment on Tuesday wouldn't she already have done it on Monday?
You don't contradict the claim "you can't lawfully use probability theory in this setting" by showing that you will be able to use probability theory if you break the setting up.
The setting is only "broken up" when she decides to leave the room, but she can think about probabilities before that. Are you saying that once she decides to leave the room, her probabilities for aspects of the external world should change?
It is completely typical for people to form probability judgements regarding what would happen if they were hypothetically to do something other than what they currently intend to do. In fact, that is the purpose of making probability judgements. If you eliminate this purpose, you can indeed say that the probability of Heads is 1/2, or 123/148, or whatever else you may please, since the choice of probability has no possible practical implications. The problem then becomes rather uninteresting, however.
Also if the Beauty changes her mind an decides to break the setting of the experiment on Tuesday wouldn't she already have done it on Monday?
That's why I specified that she changed her mind only due to an unlikely chance recollection of a conversation from years ago, which she knows would be unlikely to have happened on any previous awakening.
That's why I specified that she changed her mind only due to an unlikely chance recollection of a conversation from years ago, which she knows would be unlikely to have happened on any previous awakening.
Hmm. This opens a tangent discussion about determinism and whether the amnesia is supposed to return her to the exactly the same state as before, but thankfully we do not need to go there. We can just assume that a prince charming bursts into the room to rescue the beauty or something
The setting is only "broken up" when she decides to leave the room, but she can think about probabilities before that. Are you saying that once she decides to leave the room, her probabilities for aspects of the external world should change?
I'm saying that some of her probabilities become meaningful, even though they were not before. Tails&Monday, Tails&Tuesday, Heads&Monday become three elementary outcomes for her when she is suddenly not participating in the experiment. But when she is going along the experiment, Tails&Tuesday always follows Tails&Monday - these outcomes are causally connected and if you treat them as if they are not you arrive to the wrong conclusion.
It's easy to show that SB that every day of the experiment has a small chance of being interrupted/change her mind and walk away can correctly guess Tails with about 2/3 accuracy when she was interrupted/changed her mind. But only with 1/2 accuracy otherwise.
def interruption(heads_chance=0.5, interrupt_chance=0.001):
days, coin = classic(heads_chance=heads_chance)
for day in days:
if interrupt_chance > random.random():
return day, coin
return None, coin
interrupted_coin_guess = []
not_interrupted_coin_guess = []
for n in range(100000):
day, coin = interruption()
if day is not None:
interrupted_coin_guess.append(coin == 'Heads')
else:
not_interrupted_coin_guess.append(coin == 'Heads')
print(interrupted_coin_guess.count(True)/len(interrupted_coin_guess))
# 0.3006993006993007
print(not_interrupted_coin_guess.count(True)/len(not_interrupted_coin_guess))
# 0.5017374846029823The python code for interruption() doesn't quite make sense to me.
for day in days:
if interrupt_chance > random.random():
return day, coin
Suppose that day is Tuesday here. Then the function returns Tuesday, Tails, which represents that on a Tails Tuesday Beauty wakes up and is rescued by Prince Charming. But in this scenario she also woke up on Monday and was not rescued. This day still happened and somehow it needs to be recorded in the overall stats for the answer to be accurate.
This particular outcome is extremely rare: less then a tenth of a percent. It doesn't contribute much to the results:
interrupted_coin_guess = []
not_interrupted_coin_guess = []
for i in range(100000):
day, coin = interruption()
if day is not None:
interrupted_coin_guess.append(coin == 'Heads')
if day == 'Tuesday':
not_interrupted_coin_guess.append(coin == 'Heads')
else:
not_interrupted_coin_guess.append(coin == 'Heads')
print(interrupted_coin_guess.count(True)/len(interrupted_coin_guess))
# 0.363013698630137
print(not_interrupted_coin_guess.count(True)/len(not_interrupted_coin_guess))
# 0.501831795159256The point is that specifically in the rare outcomes where the Beauty is interrupted (some low probable random event happens and beauty notices it) she can guess Tails with 2/3 accuracy (actually a bit worse than that, the rarer the event the closer it is to 2/3) per experiment. Which she can not do when she is not interrupted.
Sure, it's rare with the given constants, but we should also be able to run the game with interrupt_chance = 0.1, 0.5, 0.99, or 1.0, and the code should output a valid answer.
Naively, if an interruption increases the probability of the coin being Tails, then not being interrupted should increase the probability of the coin being Heads. But with the current python code, I don't see that effect, trying with interrupt_chance of 0.1, 0.5, or 0.9.
Sure, it's rare with the given constants, but we should also be able to run the game with interrupt_chance = 0.1, 0.5, 0.99, or 1.0, and the code should output a valid answer.
Well, if you want to use custom chance then you shouldn't actually count not interrupted Monday if the Tuesday was interrupted. You see, here we count beauty being interrupted per experiment. If we count not interrupted Monday as a separate experiment we mess our metrics up, which isn't a big deal with very low chance of interruption but becomes relevant with custom chances.
Naively, if an interruption increases the probability of the coin being Tails, then not being interrupted should increase the probability of the coin being Heads.
If you do not count non-interrupted Monday, when Tuesday is interrupted that's indeed what happens and is clearly visible on high interruption chances. After all, if there is a highly probable event that can happen at every awakening it's much more likely not to happen if you are awaken only once. The probability of Heads on not being interrupted increases from 0.5 and approaches 1 with the interruption chance increase. This would be extremely helpful, sadly this information is unavailable. Beauty can't be shure what high likely event didn't happen in the experiment due to the memory loss - only what event didn't happen in this awakening.
This code-based approach is a very concrete approach to the problem, by the way, so thank you.
if you want to use custom chance then you shouldn't actually count not interrupted Monday if the Tuesday was interrupted.
Sure. So let's go back to the first way you had of calculating this:
for n in range(100000):
day, coin = interruption()
if day is not None:
interrupted_coin_guess.append(coin == 'Heads')
else:
not_interrupted_coin_guess.append(coin == 'Heads')
print(interrupted_coin_guess.count(True)/len(interrupted_coin_guess))
# 0.3006993006993007
The probability this is calculating is a per-experiment probability that the experiment will be interrupted. But Beauty doesn't ever get the information "this experiment will be interrupted". Instead, she experiences, or doesn't experience, the interruption. It's possible for her to not experience an interruption, even though she will later be interrupted, the following day. So this doesn't seem like a helpful calculation from Beauty's perspective, when Prince Charming busts in through the window.
The beauty gets the information "This experiment is interrupted" when she observed the interruption on her awakening. She never gets the information "This experiment is not to be interrupted" because the interruption could happen on the other awakening.
This means that specifically in the awakening that the experiment is interrupted/some random low probable event happens, the Beauty can determine how the coin landed in this particular experiment better than chance, contrary to other awakenings.
This opens a tangent discussion about determinism and whether the amnesia is supposed to return her to the exactly the same state as before, but thankfully we do not need to go there.
To briefly go there... returning her to the exactly same state would violate the no-cloning theorem of quantum mechanics. See https://en.wikipedia.org/wiki/No-cloning_theorem
I'm saying that some of her probabilities become meaningful, even though they were not before. Tails&Monday, Tails&Tuesday, Heads&Monday become three elementary outcomes for her when she is suddenly not participating in the experiment. But when she is going along the experiment, Tails&Tuesday always follows Tails&Monday - these outcomes are causally connected and if you treat them as if they are not you arrive to the wrong conclusion.
Some of her probabilities "become meaningful" in the sense that she is now more interested in them from a practical perspective. But they were meaningful beliefs before by any normal rational perspective.
I'm not sure how to continue this discussion. Your claim that Beauty's probabilities for Tails&Monday, Tails&Tuesday, and Heads&Monday need not sum to one is completely contrary to common sense, the formal theory of probability, and the way probability is used in numerous practical applications. What can I say when you deny the basis of rational discussion?
I think you have become mentally trapped by the Halfer position, and are blind to the fact that in trying to defend it you've adopted a position that is completely absurd. This may perhaps be aided by an abstract view of the problem, in which you never really consider Beauty to be an actual person. No actual person thinks in the absurd way you are advocating.
Regarding your simulation program, you build in the Halfer conclusion by apending only one guess when the experiment is not interrupted, even if the coin lands Tails.
To briefly go there... returning her to the exactly same state would violate the no-cloning theorem of quantum mechanics.
The state doesn't have to be the same up to the quantum mechanics just the same to the point that SB has the same thoughts for the same reasons and it's quite possible that QM isn't required for it. Nevertheless let's not pursue this line of inquiry anymore.
I'm not sure how to continue this discussion. Your claim that Beauty's probabilities for Tails&Monday, Tails&Tuesday, and Heads&Monday need not sum to one is completely contrary to common sense, the formal theory of probability, and the way probability is used in numerous practical applications. What can I say when you deny the basis of rational discussion?
I claim that they indeed need to sum to 1 so that we could use the formal probability theory in this setting as Kholmogorov axioms require that probability of the whole sample space was equal to one. However, they do not, as they are not three independant elementary outcomes as long as the beauty participates in the experiment. Thus we can't define probability space thus can't lawfully use the mathematical apparatus of formal probability theory.
I don't think it's fair to say that I deny the basis of rational discussion or adopted a completely absurd position. Sometimes maps do not corrspond to the territory. This includes mathematical models. There are settings in which 2+2 is not 4. There are settings where operation of "addition" cannot be defined. Likewise there are settings where probabilities of some events can not be defined. I believe Mikaël Cozic noticed one of the firsts that SB setting is problematic for certain probabilities in his paper for Double Halfer's position and the idea wasn't dismissed as a priori absurd.
I think you have become mentally trapped by the Halfer position
Actually, as you may see from the post I'm Halfer for incubator SB and Double Halfer for the classic one. And I quite understand what Thirders position in classic points to and do not have much problem with the Antropical Motte. On the contrary you claimed that all the arguments in favour of 1/2 are bad. I think, between two of us, you can be more justifiably claimed to be mentally "trapped in a position".
However, I don't think it's a fruitful direction of a discussion. I empathize how ridiculous and absurd I look from your perspective because that's exactly how you look from mine. I believe you can do the same. So let's focus on our empathy instead of outgroup mentality and keep the discussion in more respectful manner.
Regarding your simulation program, you build in the Halfer conclusion by apending only one guess when the experiment is not interrupted, even if the coin lands Tails
Of course I'm appending only one guess when the experiment is not interrupted, after all I'm, likewise, appending only one guess when the experiment is interrupted. Here I'm talking about Antropical Bailey: the ability to actually guess the coin side better then chance per experiment, not just taking advantage of a specific scoring rule.
In any case, this is beside the point. Simulation shows how just by ceasing to participate in the experiment SB's probabilities for aspects of the external world should change, no matter how counterintuitive it may sound. When the experiment is interrupted, Tails&Monday, Tails&Tuesday and Heads&Monday are not causally connected anymore, their sum becomes 1 and thriders mathematical model becomes aplicable: Beauty correctly guesses Tails 2/3 of times even though we are adding only one guess per experiment.
I'm not trying to be disrespectful here, just trying to honestly state what I think (which I believe is more respectful than not doing so).
If I understand your position correctly, you think Beauty should rationally think as follows:
- Wakes up, notices the experimenters are not here to tell her it's Wednesday and the experiment is over. Concludes it's Monday or Tuesday.
- Thinks to herself, "so, I wonder if the coin landed Heads?".
- Thinks a bit, and decides the probability of Heads is 1/2.
- Looks up and sees a dead rat crash to the ground just outside the window of her room. Thinks, "my god! I guess an eagle must have caught and killed the rat, and then lost its grip on it while flying away, and it landed outside my window!"
- Says to herself, "you know, death can come at any time..."
- Decides that wasting time on this experiment is not the right thing to do, and instead she'll leave and do something worthwhile.
- Happens to ask herself again what the probability is that the coin landed Heads.
- After thinking a bit, she decides the probability of Heads is now 1/3.
I think the combination of steps (3) and (8) is absurd. This is not how reason and reality work.
Here is how I think Beauty should rationally think:
- Beauty notices the experimenters are not here to tell her it's Wednesday and the experiment is over. Concludes it's Monday or Tuesday.
- Thinks to herself, "so, I wonder if the coin landed Heads?"
- (optional) Entertains the idea that her awakening itself is an evidence in favor of Tails, but realizes that it would be true only if her current experience was randomly sampled among three independent outcomes Tails&Monday, Tails&Tuesday and Heads&Monday, which isn't true for this experiment. Tails&Tuesday necessary follows Tails&Monday and the causal process that determines her state isn't random sample from these outcomes.
- Concludes that she doesn't have any evidence that would distinguish an outcome where coin landed Heads from the outcome where the coin landed Tails, thus keeps her prior 1/2.
- (either) Suddenly a prince bursts through the door and explains that he managed to overcome the defenses of the evil scientists keeping her here in an unlikely feat of martial prowess and is rescuing her now
- (or) The beauty has second thought about participating in the experiment. She has good reasons to stay but also some part of her wants to leave. Thankfully there is a random number generator in her room (she has another coin, for example), capable of outputting numbers in some huge interval. She thinks about a number and decides that if the generator output exactly it she will leave the room, otherwise she stays. The generator outputs the number the beauty has guessed. And she leaves.
- (or) Suddenly the beauty has panic attack that makes her leave the room immediately. She remembers that scientists told her that the experimental sleeping pills she took on Sunday have this rare side effects that can manifest in any person in 0.1% of cases in any day of the next week.
- (or) Any other event, that the beauty is rightfully confident to be low probable but possible for both Monday and Tuesday, happens. Actually even leaving the room is not necessary. The symmetry and thus the setting of the experiment is broken as long as beauty gets this new evidence. Mind you this wouldn't work with some observation which has high probability of happening - you can check it yourself with the code I provided. Likewise, it also wouldn't work if the beauty just observes any number on the random generator without precommiting to observing it in particular as it wouldn't be a rare event from her perspective. See this two posts:
https://www.lesswrong.com/posts/u7kSTyiWFHxDXrmQT/sleeping-beauty-resolved
https://www.lesswrong.com/posts/8MZPQJhMzyoJMYfz5/sleeping-beauty-not-resolved - And now, due to this new evidence, the Beauty updates to 1/3. Because now there is actually a random sampling process going on and she is twice as likely to observe the low probable outcome she has just observed when the coin is Tails
Do the steps from 4 to 8 in your example count as such evidence? They may. If it indeed was a random occurrence and not a deliberately staged performance, the rat crashing to the ground near her window is a relevant evidence! If it's surprising for you, notice that you've updated to 1/3 without any evidence whatsoever.
And yes, this is exactly how reason and reality work. Which I've shown with an actual python program faithfully replicating the logic of the experiment, that can be run on a computer from our reality. Reasoning like this, the beauty can correctly guess Tails with 2/3 probability per experiment without any shenanigans with the scoring rule.
Any other event, that the beauty is rightfully confident to be low probable but possible for both Monday and Tuesday, happens.
And since this happens absolutely every time she wakes, Beauty should always assess the probability of Heads as 1/3.
There's always fly crawling on the wall in a random direction, unlikely to be the same on Monday and Tuesday, or a stray thought about aardvarks, or a dimming of the light from the window as a cloud passes overhead, or any of millions of other things entering her consciousness in ways that won't be the same Monday and Tuesday.
If you've read the posts you link to, you must realize that this is central to my argument for why Heads has probability 1/3.
So why are you a Halfer? One reason seems to be explained by your following comment:
it also wouldn't work if the beauty just observes any number on the random generator without precommiting to observing it in particular as it wouldn't be a rare event from her perspective
But this is not how probability theory works. A rare event is a rare event. You've just decided to define another event, "random number generator produces number I'd guessed beforehand", and noted that that event didn't occur. This doesn't change the fact that the random number generator produced a number that is unlikely to be the same as that produced on another day.
But the more fundamental reason seems to be that you don't actually want to find the answer to the Sleeping Beauty problem. You want to find the answer to a more fantastical problem in which Beauty can be magically duplicated exactly and kept in a room totally isolated from the external world, and hence guaranteed to have no random experiences, or in which Beauty is a computer program that can be reset to its previous state, and have its inputs totally controlled by an experimenter.
The actual Sleeping Beauty problem is only slightly fantastical - a suitable memory erasing drug might well be discovered tomorrow, and nobody would think this was an incredible discovery that necessitates changing the foundations of probability theory or our notions of consciousness. People already forget things. People already have head injuries that make them forget everything for some period of time.
Of course, there's nothing wrong with thinking about the fantastical problem. But it's going to be hard to answer it when we haven't yet answered questions such whether a computer program can be conscious, and if so, whether consciousness requires actually running the program, or whether it's enough to set up the (deterministic) program on the computer, so that it could be run, even though we don't actually push the Start button. Without answers to such questions, how can one have any confidence that you're reasoning correctly in this situation that is far, far outside ordinary experience?
But in any case, wouldn't it be interesting and useful to first establish the answer to the actual Sleeping Beauty problem?
And since this happens absolutely every time she wakes, Beauty should always assess the probability of Heads as 1/3.
Nope. Doesn't work this way. There is an important difference between a probability of a specific low probable event happening and a probability of any low probable event from a huge class of events happening. Unsurprisingly, the former is much more probable than the latter and the trick works only with low probable events. As I've explicitly said, and you could've checked yourself as I provided you the code for it.
It's easy to see why something that happens absolutely every time she wakes doesn't help at all. You see, 50% of the coin tosses are Heads. If Beauty correctly guessed Tails 2/3 out of all experiments that would be a contradiction. But it's possible for the Beauty to correctly guess Tails 2/3 out of some subset of experiments. To get the 2/3 score she need some kind of evidence that happens more often when the coin is Tails than when it is Heads, not all the time, and then guess only when she gets this evidence.
There's always fly crawling on the wall in a random direction, unlikely to be the same on Monday and Tuesday, or a stray thought about aardvarks, or a dimming of the light from the window as a cloud passes overhead, or any of millions of other things entering her consciousness in ways that won't be the same Monday and Tuesday.
This is irrelevant unless the Beauty somehow knows where the fly is supposed to be on Monday and where on Tuesday. She can try to guess tails when the fly is in a specific place that the beauty precommited to, hoping that the causal process that define fly position is close enough to placing the fly in this place with the same low probability for every day but it's not guaranteed to work.
If you've read the posts you link to, you must realize that this is central to my argument for why Heads has probability 1/3.
I've linked two posts. You need to read the second one as well, to understand the mistake in the reasoning of the first.
But this is not how probability theory works. A rare event is a rare event. You've just decided to define another event, "random number generator produces number I'd guessed beforehand", and noted that that event didn't occur. This doesn't change the fact that the random number generator produced a number that is unlikely to be the same as that produced on another day.
This is exactly how probability theory works. The event "random number generator produced any number" has very high probability. The event "random number generator produced this specific number" has low probability. Which event we are talking about depends on whether the number was specified or not. It can be confusing if you forget that probabilities are in the mind, that it's about Beauty decision making process, not the metaphysical essence of randomness.
You want to find the answer to a more fantastical problem in which Beauty can be magically duplicated exactly and kept in a room totally isolated from the external world, and hence guaranteed to have no random experiences
The fact that Beauty is unable to tell which day it is or whether she has been awakened before is an important condition of the experiment.
But this doesn't have to mean that her experiences on Monday and Tuesday or on Heads and Tails are necessary exactly the same - she just doesn't have to be able to tell which is which. Beauty can be placed in the differently colored rooms on Monday&Tails, Monday&Heads and Tuesday&Tails. All the furniture can be completely different as well. There can be ciphered message describing the result of the coin toss. Unless she knows how to break the cipher, or knows the pattern in colors/furniture this doesn't help her. The mathematical model is still the same.
On a repeated experiment beauty can try executing a strategy but this requires precommitment to this strategy. And without this precommitment she will not be able to get useful information from all the differences in the outcomes.
But it's going to be hard to answer it when we haven't yet answered questions such whether a computer program can be conscious, and if so, whether consciousness requires actually running the program, or whether it's enough to set up the (deterministic) program on the computer, so that it could be run, even though we don't actually push the Start button.
How is the consciousness angle relevant here? Are you under the impression that probability theory works differently depending on whether we are reasoning about conscious or unconscious objects?
Nope. Doesn't work this way. There is an important difference between a probability of a specific low probable event happening and a probability of any low probable event from a huge class of events happening.
In Bayesian probability theory, it certainly does work this way. To find the posterior probability of Heads, given what you have observed, you combine the prior probability with the likelihood for Heads vs. Tails based on everything that you have observed. You don't say, "but this observation is one of a large class of observations that I've decided to group together, so I'll only update based on the probability that any observation in the group would occur (which is one for both Heads and Tails in this situation)".
You're arguing in a frequentist fashion. A similar sort of issue for a frequentist would arise if you flipped a coin 9 times and found that 2 of the flips were Heads. If you then ask the frequentist what the p-value is for testing the hypothesis that the coin was fair, they'll be unable to answer until you tell them whether you pre-committed to flipping the coin 9 times, or to flipping it until 2 Heads occurred (they'll be completely lost if you tell them you just flipped until your finger got tired). Bayesians think this is ridiculous.
Of course, there are plenty of frequentists in the world, but I presume they are uninterested in the Sleeping Beauty problem, since to a frequentist, Beauty's probability for Heads is a meaningless concept, since they don't think probability can be used to represent degrees of belief.
How is the consciousness angle relevant here? Are you under the impression that probability theory works differently depending on whether we are reasoning about conscious or unconscious objects?
I think if Beauty isn't a conscious being, it doesn't make much sense to talk about how she should reason regarding philosophical arguments about probability.
I suspect we're at a bit of an impasse with this line of discussion. I'll just mention that probability is supposed to be useful. And if you extend the problem to allow Beauty to make bets, in various scenarios, the bets the make Beauty the most money are the ones she will make by assessing the probability of Heads to be 1/3 and then applying standard decision theory. Halfers are losers.
You are making a fascinating mistake, and I may make a separate post about it, even though it's not particularly related to anthropics and just a curious detail about probability theory, which in retrospect I relize I was confused myself about. I'd recommend you to meditate on it for a while. You already have all the information required to figure it out. You just need to switch yourself from the "argument mode" to "investigation mode".
Here are a couple more hints that you may find useful.
1) Suppose you observed number 71 on a random number generator that produces numbers from 0 to 99.
Is it
- 1 in 100 occurence because the number is exactly 71?
- 1 in 50 occurence becaue the number consist of these two digits: 7 and 1?
- 1 in 10 occurence because the first digit is 7?
- 1 in 2 occurence because the number is more or equal 50?
- 1 in n occurence because it's possible to come with some other arbitrary rule?
What determine which case is actually true?
2) Suppose you observed a list of numbers with length n, produced by this random number generator. The probability that exactly this series is produced is
- At what n are you completely shocked and in total disbelief about your reality, after all you've just observed an event that your model of reality claims to be extremely improbable?
- Would you be more shocked if all the numbers in this list are the same? If so why?
- Can you now produce arbitrary improbable events just by having a random number generator? In what sense are these events have probability if you can witness as many of them as you want any time?
You do not need to tell me the answers. It's just something I believe will be helpful for you to honestly think about.
To find the posterior probability of Heads, given what you have observed, you combine the prior probability with the likelihood for Heads vs. Tails based on everything that you have observed.
Here is the last hint, actually I have a feeling that this just spoils the solution outright so it's in rot13:
Gur bofreingvbaf "Enaqbz ahzore trarengbe cebqhprq n ahzore" naq "Enaqbz ahzore trarengbe cebqhprq gur rknpg ahzore V'ir thrffrq" ner qvssrerag bofreingvbaf. Lbh pna bofreir gur ynggre bayl vs lbh'ir thrffrq n ahzore orsberunaq. Lbh znl guvax nobhg nf nal bgure novyvgl gb rkgenpg vasbezngvba sebz lbhe raivebazrag.
Fhccbfr jura gur pbva vf Gnvyf gur ebbz unf terra jnyyf naq jura vg'f Urnqf gur ebbz unf oyhr jnyyf. N crefba jub xabjf nobhg guvf naq vfa'g pbybe oyvaq pna thrff gur erfhyg bs n pbva gbff cresrpgyl. N pbybe oyvaq crefba jub xabjf nobhg guvf ehyr - pna'g. Rira vs gurl xabj gung gur ebbz unf fbzr pbybe, gurl ner hanoyr gb rkrphgr gur fgengrtl "thrff Gnvyf rirel gvzr gur ebbz vf terra".
N crefba jub qvqa'g thrff n ahzore orsberunaq qbrfa'g cbffrff gur novyvgl gb bofreir rirag "Enaqbz ahzore trarengbe cebqhprq gur rknpg ahzore V'ir thrffrq" whfg nf n pbybe oyvaq crefba qbrfa'g unir na novyvgl gb bofreir na rirag "Gur ebbz vf terra".
I think if Beauty isn't a conscious being, it doesn't make much sense to talk about how she should reason regarding philosophical arguments about probability.
The Beauty doesn't need to experience qualia or be self aware to have meaningful probability estimate.
I'll just mention that probability is supposed to be useful. And if you extend the problem to allow Beauty to make bets, in various scenarios, the bets the make Beauty the most money are the ones she will make by assessing the probability of Heads to be 1/3 and then applying standard decision theory.
Betting arguments are not particularly helpful. They are describing the motte - specific scoring rule, and not the actual ability to guess the outcome of the coin toss in the experiment. As I've written in the post itself:
As long as we do not claim that this fact gives an ability to predict the result of the coin toss better than chance, then we are just using different definitions, while agreeing on everything. We can translate from Thirder language to mine and back without any problem. Whatever betting schema is proposed, all other things being equal, we will agree to the same bets.
That is, if betting happens every day, Halfers and Double Halfers need to weight the odds by the number of bets, while Thirders already include this weighting in their definitions "probability". On the other hand, if only one bet per experiment counts, suddenly it's thirders who need to discount this weighting from their "probability" and Halfers and Double Halfers who are fine by default.
There are rules for how to do arithmetic. If you want to get the right answer, you have to follow them. So, when adding 18 and 17, you can't just decide that you don't like to carry 1s today, and hence compute that 18+17=25.
Similarly, there are rules for how to do Bayesian probability calculations. If you want to get the right answer, you have to follow them. One of the rules is that the posterior probability of something is found by conditioning on all the data you have. If you do a clinical trial with 1000 subjects, you can't just decide that you'd like to compute the posterior probability that the treatment works by conditioning on the data for just the first 700.
If you've seen the output of a random number generator, and are using this to compute a posterior probability, you condition on the actual number observed, say 71. You do not condition on any of the other events you mention, because they are less informative than the actual number - conditioning on them would amount to ignoring part of the data. (In some circumstances, the result of conditioning on all the data may be the same as the result of conditioning on some function of the data - when that function is a "sufficient statistic", but it's always correct to condition on all the data.)
This is absolutely standard Bayesian procedure. There is nothing in the least bit controversial about it. (That is, it is definitely how Bayesian inference works - there are of course some people who don't accept that Bayesian inference is the right thing to do.)
Similarly, there are certain rules for how to apply decision theory to choose an action to maximize your expected utility, based on probability judgements that you've made.
If you compute probabilities incorrectly, and then incorrectly apply decision theory to choose an action based on these incorrect probabilities, it is possible that your two errors will cancel out. That is actually rather likely if you have other ways of telling what the right answer is, and hence have the opportunity to make ad hoc (incorrect) alterations to how you apply decision theory in order to get the right decision with the wrong probabilities.
If you'd like to outline some specific betting scenario for Sleeping Beauty, I'll show you how applying decision theory correctly produces the right action only if Beauty judges the probability of Heads to be 1/3.
Of course, there are plenty of frequentists in the world, but I presume they are uninterested in the Sleeping Beauty problem, since to a frequentist, Beauty's probability for Heads is a meaningless concept, since they don't think probability can be used to represent degrees of belief.
Tangent: I ran across an apparently Frequentist analysis of Sleeping Beauty here: Sleeping Beauty: Exploring a Neglected Solution, Luna
To make the concept meaningful under Frequentism, Luna has Beauty perform an experiment of asking the higher level experimenters which awakening she is in (H1, T1, or T2). If she undergoes both sets of experiments many times, the frequency of the experimenters responding H1 will tend to 1/3, and so the Frequentist probability is similarly 1/3.
I say "apparently Frequentist" because Luna doesn't use the term and I'm not sure of the exact terminology when Luna reasons about the frequency of hypothetical experiments that Beauty has not actually performed.
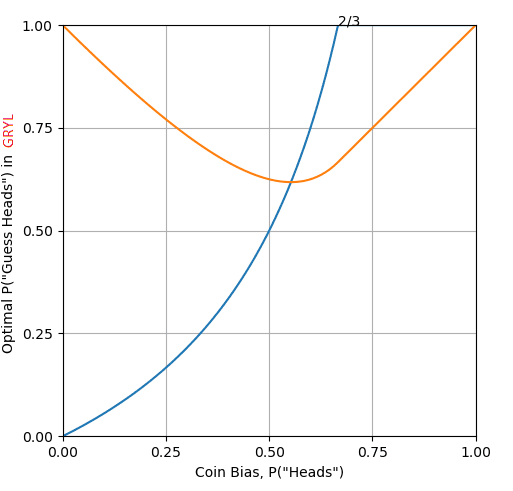
This is the first post in my series on Anthropics. The next one is Conservation of Expected Evidence and Random Sampling in Anthropics
Introduction
There is a curious Motte-and-Bailey dynamic going on with anthropic reasoning. The Motte is that it's just about a specific scoring rule and a corresponding way to define probability estimates. The Bailey is that we have psychic powers to blackmail reality by creating copies of our minds or using amnesia drugs. I'm going to explore these dynamics using two version of the famous Sleeping Beauty mind experiment: classical with the amnesia drug, and incubator, where either one or two Beauties are created. Simultaneously, I'll showcase the dissimilarities between them.
As far as I know people, who are Thirders in classical Sleeping Beauty, are also Thirders in the incubator version for mostly the same reasons. The SIA school of anthropics considers 1/3 to be the correct answer in both problems. And yet these problems are quite different. Adam Elga's proof for thirdism definitely doesn't work for the incubator version. Reasons for answering 1/2 are also different: Double Halfer in one and Halfer in the other.
Classic version of Sleeping Beauty
Let's start from the original version of the experiment
Here is a simple implementation in Python
First, let's clear out what I mean by different scoring rule producing either 1/3 or 1/2.
That is, depending on whether we count per day or per experiment we get different answers, upon running the experiment multiple times. This is completely unsurprising.
Personally, I've always answered 1/2 in Sleeping Beauty and found the Thirders approach silly. Clearly, my credence for Heads should represent the probability of the coin actually landing Heads per toss, not per my guess! For example, in the Monty Hall problem my credence of winning on a door switch is 2/3 not because now I make two guesses instead of one, but because I actually win two out of three times this way in a repeated experiment. If my credence for a coin being Heads is 1/3 and in reality, if we do the same experiment a hundred times, in about fifty of them the coin is heads - then it's an obvious example of a map not representing the territory - which is quite understandable considering the usage of the amnesia drug.
Yet, even I can appreciate that the Thirders position points to something. If we specifically care about subjective experience, than indeed two thirds of them are going to be when the coin is Tails. As long as we do not claim that this fact gives an ability to predict the result of the coin toss better than chance, then we are just using different definitions, while agreeing on everything. We can translate from Thirder language to mine and back without any problem. Whatever betting schema is proposed, all other things being equal, we will agree to the same bets.
This is what I call the Anthropic Motte. The Bailey is the claim that the coin is actually more likely to be Tails when I participate in the experiment myself. That is, my awakening on Monday or Tuesday gives me evidence that lawfully update me to thinking that the coin landed Tails with 2/3 probability in this experiment, not just on average awakening.
This Bailey has originated from anthropic theories, talking about "updating on existence" such as SIA and SSA and will be more evident in the incubator version of the Sleeping Beauty. But first let's have a look at the Adam Elga's paper Self-locating belief and the Sleeping Beauty problem with a proof for Thirdism, which, I believe has also contributed to the Bailey and the confusion between it and the Motte.
On Adam Elga's proof for Thirdism
I find a lot of issues with it, following from what the author acknowledges himself:
Basically, you can't lawfully use probability theory in this setting assuming that Tails and Monday, Tails and Tuesday and Heads and Monday are three exhaustive and exclusive outcomes which probabilities are supposed to be added to 1. T1 are causally connected to T2, they happen to the same person, even if this person doesn't remember it.
According to Elga:
P(Tuesday|Tails)P(Tails)=P(Tails∩Tuesday)=1/3
However
P(Tuesday|Tails)=1/2
And so
P(Tails)=2/3
Notice that it's just the probability of Tails, not probability of Tails conditional on awakening - the model Adam Elga uses doesn't account for such things at all, so all the justifications based on the updating on awakening are inappropriate here.
This, of course, directly contradicts the initial claim that the coin is fair, which is, among other things, used to prove that
P(Tails|Monday)=P(Heads|Monday) = 1/2
Now, whether the statement above is true or not, is a big deal. And not only because it's crucial for Adam Elga's proof. Among those who give the answer 1/2 in the Sleeping Beauty experiment there are two distinct positions: Halfers who do not agree with this statement and Double Halfers who do. Thankfully this disagreement is easy to solve.
That is, if the Beauty knows that she is awake on Monday it doesn't give her any information whether the coin landed Heads or Tails. This is expected because Beauty was supposed to be awoken on Monday regardless of the coin toss result, moreover she could've been awaken on Monday even before the coin toss was made. If the credence for Heads in such situation was anything but 1/2 it would mean that participation in the experiment gave the Sleeping Beauty psychic powers to predict the result of the fair coin toss better than chance.
To conclude, in the classic Sleeping Beauty experiment, regardless of what you mean by credence that the coin is Heads, 50% of coin tosses are Heads, Sleeping Beauty doesn't have a better way to determine them than chance and knowing that the current day is Monday doesn't help either.
Incubator version of Sleeping Beauty
Now, let's look at the incubator version of Sleeping Beauty, where there is no sleeping drug or memory loss, but either one or two Beauties are created based on the result of the coin toss.
Here is the implementation of this scenario
This version of experiment evades the previous critique. Outcomes T1 and T2 are not causally connected, are randomly selected and do not happen to the same participant in different time.
However, Elga's proof won't work in this situation for a different reason.
Suppose someone left a definitive clue in Room 1 that it's indeed Room 1. This time it will be relevant new information as, finding yourself in Room 1 is twice more likely if the coin is Heads.
P(Heads|Room1)=2P(Tails|Room1)
A crucial element of Elga's proof isn't satisfied. In this case Halfers' reasoning is correct and Double Halfers' is wrong. We can see it on the repeated experiment
So even if you believe that Adam Elga's proof for Thirdism is sound in the classical version of Sleeping Beauty, it's not applicable for the incubator version. It can't be the justification for answering 1/3 in both cases. Likewise the reasons to answer 1/2 are different in both experiments.
Anthropical Motte here is to claim that Beauties care for each other and invoke total utilitarianism. Being right on Tails means that two Beauties are right, while being right on Heads - that only one. Such attempt to construct the same scoring rule as with the classical version makes it completely clear that we are not talking about probability of coin being Heads or Tails anymore, but about the expected utility of the answer.
The Bailey is that you in particular are going to find yourself in the Tails world more likely if you were created during the experiment. Not that just on average most people created in such experiments are created when the coin landed tails. You in particular can guess that coin landed tails with 2/3 probability if you were part of the experiment due to the update on your existence. That the chance that there is another version of you in the different room is 2/3.
Final words on Anthropical Motte and Bailey
People do not usually hold both the Anthropical Motte and the Anthropical Bailey positions simultaneously. It's easy to see that if your scoring rule counted guesses every day/per every Beauty and it was 2/3 times likely that the coin landed Tails, then you should be not Thirder but Fifther.
Instead, people just assume that they are the same position, switching between them back and forth, often without noticing. This is understandable because usually they are! Usually if two thirds of your subjective experiences happen when the coin is Tails, Tails outcome of the coin toss are two times more likely. Usually if something is true on average for 2/3 of the population, it is 2/3 likely true for you as well. Sleeping Beauty cases are just specifically designed as adversarial attacks on this heuristic. Of course some people are confused.
Let's get rid of this confusion. Anthropical Motte and Bailey are two different things. And while the Motte is fine, the Bailey is responsible for, or at least, a serious symptom of much of absurdity of anthropic reasoning, which I'm going to resolve in the series of future posts.
The next post in the series is Conservation of Expected Evidence and Random Sampling in Anthropics.