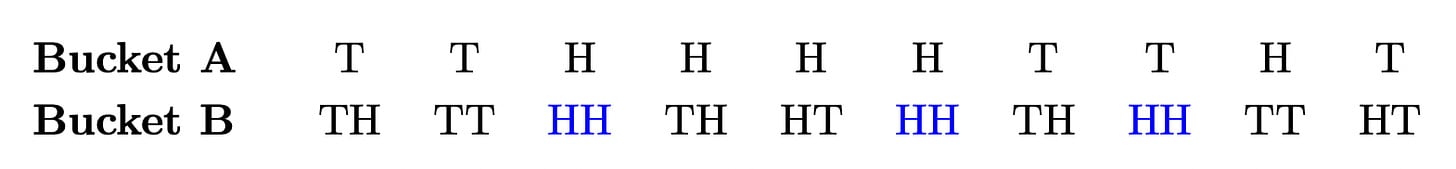(Co-written with Bernhard Salow)

TLDR: Differential legibility is a pervasive, persistent, and individually-rational source of unfair treatment. Either it’s a purely-structural injustice, or it’s a type of "zetetic injustice"—one requiring changes to our practices of inquiry.

Finally, graduate admissions are done. Exciting. Exhausting. And suspicious.

Yet again, applicants from prestigious, well-known universities—the “Presties”, as you call them—were admitted at a much higher rate than others.

But you’re convinced that—at least controlling for standardized-test scores and writing samples—prestige is a sham: it’s largely money and legacies that determine who gets into prestigious schools; and such schools train their students no better.

Suppose you’re right.

Does that settle it? Is the best explanation for the Prestie admissions-advantage that your department has a pure prejudice toward fancy institutions?

No. There’s a pervasive, problematic, but individually rational type of bias that is likely at play. Economists call it “statistical discrimination” (or "screening discrimination"). 

But it’s about uncertainty, not statistics. We’ll call it Bayesian injustice.

A simplified case

Start with a simple, abstract example. Two buckets, A and B, contain 10 coins each. The coins are weighted: each has either a ⅔ or a ⅓ chance of landing heads when tossed. Their weights were determined at random, independently of the bucket—so you expect the two buckets to have the same proportions of each type of coin.

You have to pick one coin to bet will land heads on a future toss. 

To make your decision, you’re allowed to flip each coin from Bucket A once, and each coin from Bucket B twice. Here are the outcomes:

Which coin are you going to bet on? One of the ones (in blue) that landed heads twice, of course! These are the coins that you should be most confident are weighted toward heads, since it’s less likely that two heads in a row was a fluke that that one was. 

Although the proportions of coins that are biased toward heads is the same in the two buckets, it’s easier to identify a coin from Bucket B that has good chance to land heads. As we might say: the coins from Bucket B are more legible than those from Bucket A, since you have more information about them.

This generalizes. Suppose there are 100 coins in each bucket, you can choose 10 to bet on landing heads, and you are trying to maximize your winnings. Then you’ll almost certainly bet on only coins from Bucket B (since almost certainly at least 10 of them will land HH).

End of abstract case.

The admissions case

If you squint, you can see how this reasoning will apply to graduate admissions. Let’s spell it out with a simple model.

Suppose 200 people apply to your graduate program. 100 are from prestigious universities—the Presties—and 100 are from normal universities—the Normies.

What your program cares about is some measure of qualifications, q_i, that each candidate i has. For simplicity, let's let q_i = the objective chance of completing your graduate program. 

You don’t know what q_i is in any given case. It ranges from 0–100%, and the committee is trying to figure out what it is for each applicant. To do so, they read the applications and form rational (Bayesian) estimates for each applicant’s chance of success (q_i), and then admit the 10 applicants with the highest estimates.

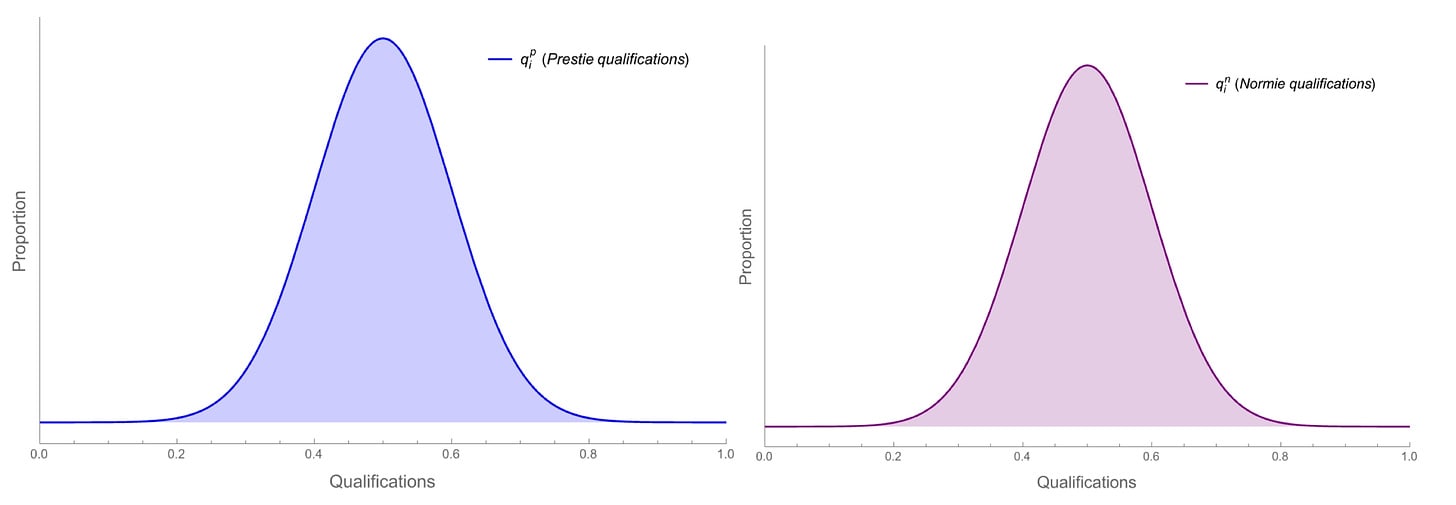
Suppose you know—since prestige is a sham—that the distribution of candidate qualifications is identical between Presties and Normies. For concreteness, say they’re both normally distributed with mean 50%:

Each application gives you an unbiased but noisy signal, 𝞱_i, about candidate i’s qualifications q_i.^[1]

Summarizing: you know that each Prestie and Normie candidate is equally likely to be equally qualified, and that you’ll get only unbiased information about each. Does it follow that—if you’re rational and unbiased—you’ll admit Presties and Normies at equal rates?

No! Given your background information, it’s likely that the Prestie applications are more legible than the Normie ones.

Why? Because you know the prestigious schools. You’ve had students from them. You’ve read many letters from their faculty. You have a decent idea how much coaching has gone into their application. And so on.

Meanwhile, you’re much less sure about the Normie applications. You barely know of some of the schools. You haven’t had any students from them. You don’t know the letter-writers. You have little idea how much coaching (or other opportunities) the students have had. And so on.

This difference in background knowledge makes the Prestie applications more legible than the Normie ones—makes you less uncertain about what to think upon reading their application. In other words: Prestie applications are like coins from Bucket B that you get to toss twice instead of just once.^[2]

Why does this matter? Because—as with our coins example—the more uncertainty you should have about a signal’s reliability (the less legible it is), the less it should move your estimates from your priors.

Imagine two letter-writers—Nolan and Paige—each tell you that their respective candidates (Nigel and Paula) have a 80% chance of completing your graduate program.

Paige is at a prestigious school. You know her well, and have had enough experience with her letters to know how reliable they are. Given that, her letter is a clear signal: your estimate of Paula’s qualifications should move up from 50% to close to 80%.

Meanwhile, you don’t know Nolan at all, so you’re uncertain how reliable his letters are. He could, of course, be more reliable than Paige; but he could also be extremely unreliable. If you knew the former, you’d move your estimate of Nigel’s chances all the way to 80%; if you knew the latter, you’d leave it at 50%. So when you’re uncertain, the rational thing to do is hedge—for example, to wind up with an estimate of 60%.

This generalizes. When you have more uncertainty about the reliability of source, your estimates should be less sensitive to that source’s information (and more dependent on your priors).

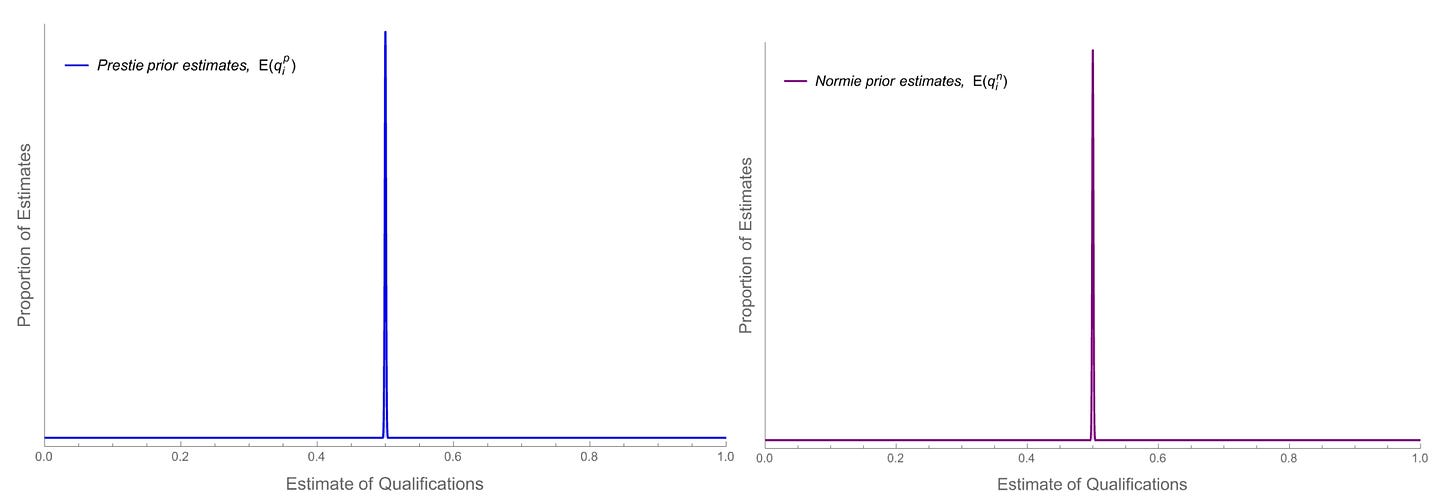
Given this, what happens to your estimates of the qualifications of the whole pool of applicants? You start out with the same prior estimate of q_i = 50% for every candidate in each group:

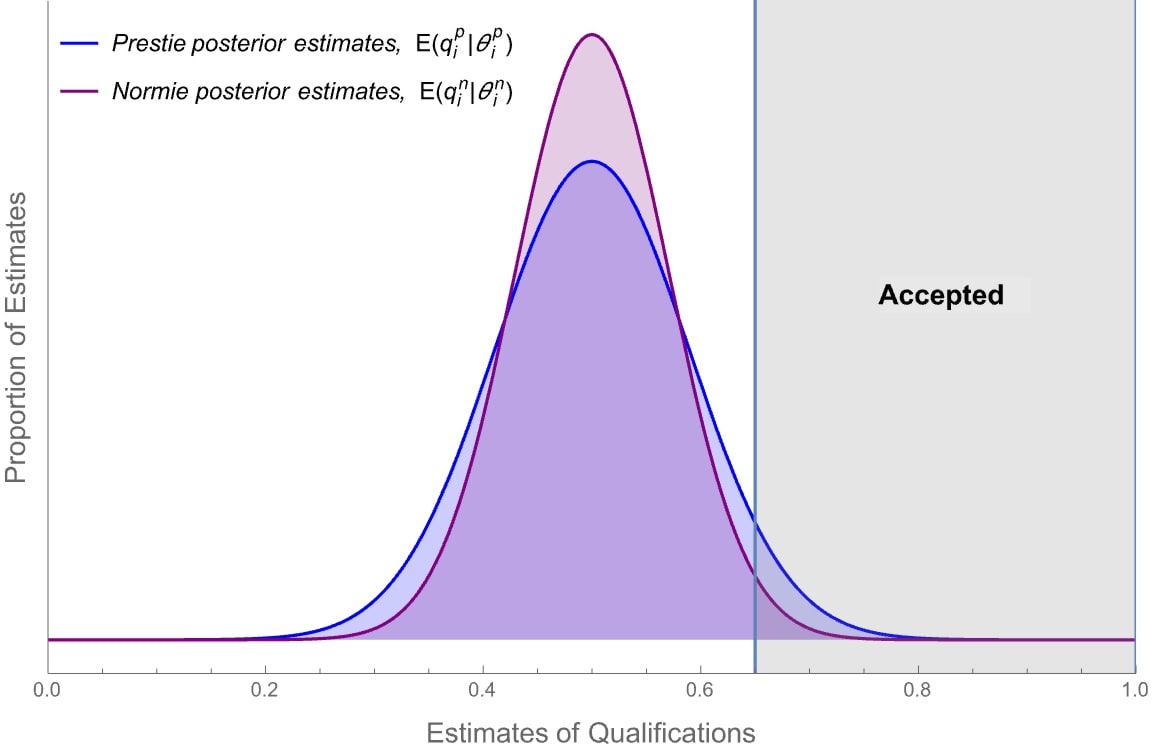
Once you get the signals, your estimates spread out—some candidates had strong applications, others had weak ones. But the Prestie signals are (on average) more legible. As a result, your estimates for the qualifications of various Presties will spread out more:

Remember that you’ll accept the 10 candidates that you have the highest estimates of. This determines an upper region—say the gray one—in which you accept all the candidates. But because your Prestie-estimates are more spread out, there are far more Presties than Normies in this Accepted (gray) region.

The upshot? Despite the fact that you know the two groups have the same distribution of qualifications and you process the evidence in an unbiased way, you’re still better at identifying the qualified Prestie candidates.

Though rational—indeed, optimal from the point of view of accurately estimating candidate’s qualifications—the result is seriously unfair. For example, in the above plots, Prestie signals have a standard deviation of 5% while Normies have one of 10%.  As a result:

• If you admit 10 candidates, the median class will have 8 Presties, and most (84%) of the time, you’ll admit more Presties than Normies.
• If Paula (a Prestie) and Nigel (a Normie) are in fact equally qualified (q_i = 70%), Paula is far more likely (73%) to be admitted than Nigel is (26%).

That looks like a form of epistemic injustice.

Why does this matter?

How common is Bayesian injustice? It’ll arise whenever there’s both (1) a competitive selection process, and (2) more uncertainty about (i.e. less legibility of) the signals from one group than another.

So it’s everywhere:

Who you know. Qualified candidates who are more familiar to a committee (through networking or social connections) will be more legible.

Who you are. Qualified candidates who are in the mainstream (of society, or a subfield) will be more legible.

What you face. Qualified candidates who are less likely to face potential obstacles will provide fewer sources of uncertainty, so will be more legible.

Who you’re like. Qualified candidates who are similar to known, successful past candidates will be more legible.

This is clearly unfair. Is it also unjust?

We think sometimes it clearly is—for example, when candidate legibility correlates with class, race, gender, and other socially fraught categories. (As it often will.) Graduate admissions is a simple case to think about, but the dynamics of Bayesian injustice crop up in every competitive selection process: college admissions; publication; hiring; loan decisions; parole applications; you name it.

Yet Bayesian injustice results from individually rational (and even well-meaning!) behavior. So where do we point the blame?

Two options.

First, we could say that it is an epistemic version of a tragedy of the commons: each individual is blameless—the problem is simply the structure that makes for differential legibility. In other words, Bayesian injustice is a structural injustice.

But that diagnosis might breed complacency—“That’s not our problem to address; it’s society’s", people might say.

Alternatively, we could say that individuals who perpetrate Bayesian injustices are violating a zetetic duty: a duty regulating how you gather and manage evidence. The problem arises because, by default, committees get better evidence about Presties than Normies. Thus they might have a duty of zetetic justice to try to equalize their evidence about candidates from each group. How?

One option is to level down: ignore extra information about more-legible candidates, insofar as they can. Bans on interviews, standardization of applications, and limitations of communication to formal channels during interview processes are all ways to try to do this.

Another option is to level up: devote more resources to learning about the less-legible candidates. Extra time discussing or learning about candidates from under-represented backgrounds, programs that attempt to give such candidates access to professional networks and coaching, and many other DEI efforts can all be seen as attempts to do this.

Obviously there’s no one-size-fits-all response. But equally obviously—we think—some response is often called for. When society makes life systematically harder for some people, something should be done. All the more so when the problem is one that individually rational, well-meaning people will automatically perpetuate. Leveling-up and leveling-down—within reason—can both be justified responses.

Still, the fact that this is individually rational matters. The possibility of Bayesian injustice shows that the existence of unfair outcomes doesn’t imply that those involved in the selection processes are prejudiced or biased.

It also explains why jumping to such conclusions may backfire: if Bayesian injustice is at play, selectors may be (rationally!) convinced that prejudice is not the driver of their decisions—making them quick to dismiss complaints as ill-informed or malicious.

So? Having more people more aware of the possibility of Bayesian injustice should allow for both more accurate diagnoses and more constructive responses to the societal injustices that persist. We hope.

What next?

If you liked this post, subscribe to my Substack for future posts.

For recent philosophy papers where we think Bayesian injustice is the background explanation, see Heesen 2018 on publication bias, Hedden 2021 on algorithmic fairness, and the exchange between Bovens 2016 and Mulligan 2017 on shortlisting in hiring decisions.

For classic economics paper on statistical discrimination, see Phelps 1972 and Aigner and Cain 1977; for the paper that coined "screening discrimination", see Cornell and Welch 1996.

1. ^{^}

   So 𝞱_i = q_i +𝟄_i, with 𝟄_i normally distributed with mean 0.

2. ^{^}

   Formally, the signals 𝞱_i have less variance for Prestie applications than Normie ones, and so are better indicators of their qualifications level q_i.