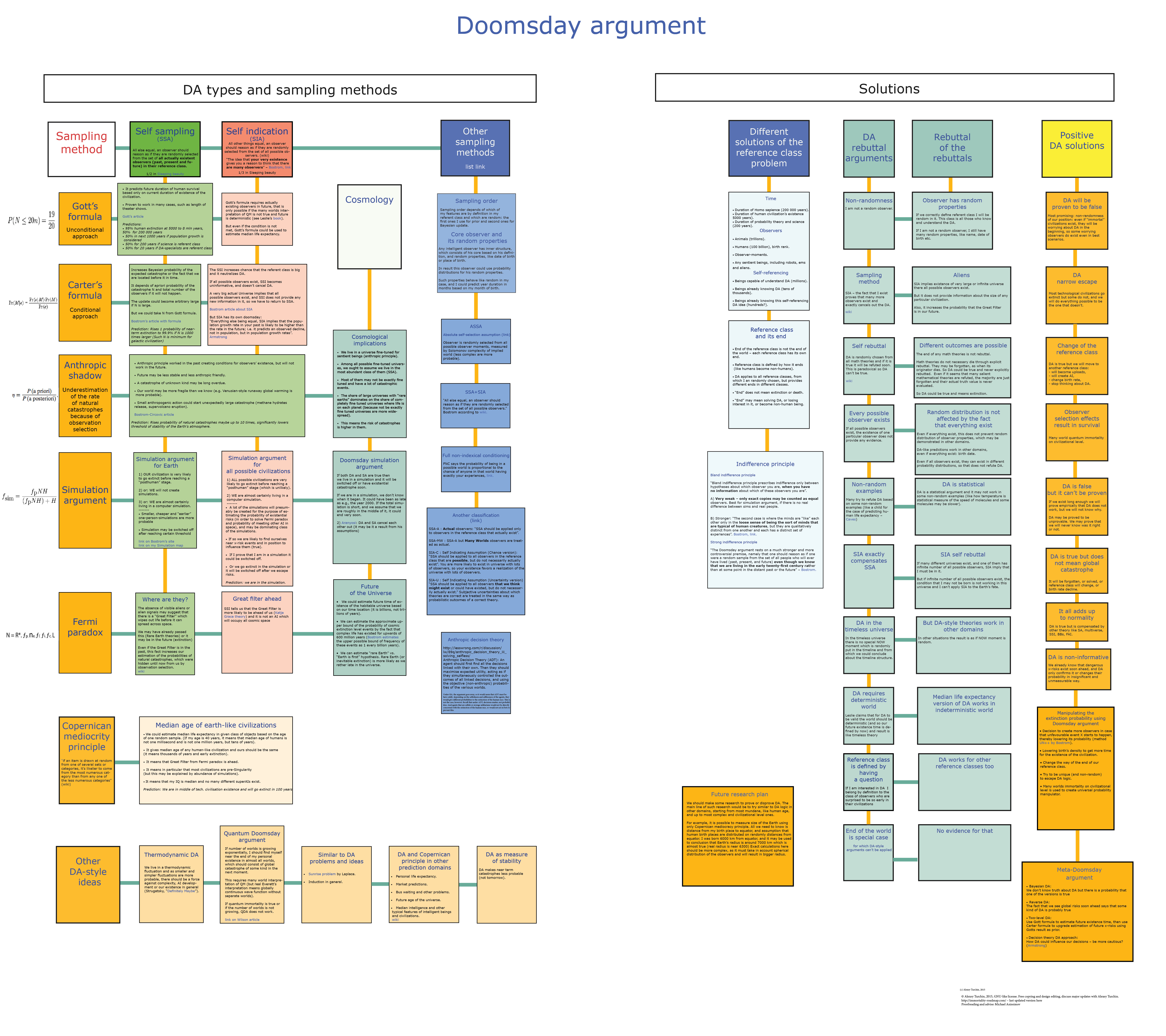
Doomsday Argument Map
3Avo
1turchin
1Avo
1turchin
1Avo
5turchin
0gjm
3turchin
0Avo
1gjm
1turchin
3entirelyuseless
3turchin
-1Avo
1turchin
-1Avo
1turchin
0Avo
1turchin
1Avo
1turchin
0Avo
1turchin
-1Lumifer
3turchin
0Lumifer
3turchin
0Lumifer
1turchin
0selylindi
1Vaniver
0turchin
New Comment
I've been doing some more reading on DA, and I now believe that the definitive argument against it was given by Dennis Dieks in his 2007 paper "Reasoning about the future: Doom and Beauty". See sections 3 and 4. The paper is available at http://www.jstor.org/stable/27653528 or, in preprint form, at http://www.cl.cam.ac.uk/~rf10/doomrev.pdf Dieks shows that a consistent application of DA, in which you use the argument that you are equally likely to be any human who will ever live, requires you to first adjust the prior for doom that you would have used (knowing that you live now). Then, inserting the adjusted prior into the usual DA formula simply gives back your original prior! Brilliant, and (to me) utterly convincing.
Thanks for the link. Does it work on toy models of DA in other domains?
For example, if I ask your age and you will say "30 years old" (guessing), I can conclude from it that medium human life expectancy is around several decades years with 50 per cent confidence, and that it is less than 1000 years with 95 per cent confidence.
Which priors I am using here?
For a general analysis along the same lines of life expectancies of various phenomena, see Carl Caves, "Predicting future duration from present age: Revisiting a critical assessment of Gott's rule", http://arxiv.org/abs/0806.3538 . Caves shows (like Dieks) that the original priors are the correct ones. In my example of the biologist and the the bacterium, the biologist is correct.
I know the paper, read it and found a mistake. The mistake is that while illustrating his disproval of DA, he creates special non random case, something like 1 month child for estimation of median life expectancy. It means that he don't understand the main idea of DA logic, that is we should use one random sample to estimate total set size.
Why is that case "non random"? A randomly selected person could well turn out to be a 1 month old child. If you know in advance that this is not typical, then you already know something about median life expectancy, and that is what you are using to make your estimate, not the age of the selected person.
Do you have a criticism of Caves' detailed mathematical analysis? It seems definitive to me.
And: to the person who keeps downvoting me. Are you treating my "arguments as soldiers", or do you have a rational argument of your own to offer?
In Cave case this argument was nonrandom, because he knew that median life expectancy was 80 years, and deliberately choose extremely young person. So he was cheating. If he would need really random person he should apply to him self or reader. It will be real experiment. I decided not to search math errors in his calculations, because I don't agree this his notion of "randomness".
I don't see how this is cheating. Cave's central claim is this (paraphrased rather than quoted): "If you wish to predict how long something will last on the basis of how long it has existed so far, and you have any further information about relevant time scales, then the DA will give bad predictions because it implicitly uses a prior that's invariant under temporal scaling."
He agrees that if you take a thousand random people and proclaim that half of them are in the first halves of their lives, you will probably be about right. But he disagrees with any version of the DA that says that for each of those people you should assign a 0.5 probability that they're in the first half of their life -- because you have some further information about human lifespans that you should be taking into account.
Cases in which the DA is applied usually have vaguer information about relevant timescales; e.g., if you want to predict how long the US will continue to exist as a nation, there are all kinds of relevant facts but none of them quite takes the form "we have a huge sample of nations similar to the US, and here's how their lifetimes were distributed". But usually there are some grounds for thinking some lifetimes more credible than others in advance of discovering how long the thing has lasted so far (e.g., even if you had no idea when the US came into existence you would be pretty surprised to find it lasting less than a week or more than a million years). And, says Caves, in that situation your posterior distribution for the total lifespan (after discovering how long the thing has existed so far) should not be the one provided by the DA.
So the examples he should be looking at are exactly ones where you have some prior information about lifespan; and the divergence between the "correct" posterior and the DA posterior, if Caves is right, should be greatest for examples whose current age is quite different from half the typical lifespan. So how's it cheating to look at such examples?
Basically, there is nothing do disagree here: DA is working, but gives weaker predictions, than actual information about distributions. That is why we should try to use DA in domains where we don't have initial distribution, just to get order of magnitude estimation.
The more interesting question is how to combine situations where we have some incomplete information about actual distribution and the age of one random object. It seems that Caves suggest to ignore DA in this case. (But there is also Carter's approach to DA, where DA inference is used to update information about known future x-risks, based on fact that we are before it.)
In some cases DA may be stronger than incomplete information provided by other sources. For example, if one extraterrestrial knows for sure, that any mammal life expectancy is less than 1 million years, and than he finds one human being with age 60 years, DA gives him that medium human life expectancy is less than 1000 years. In this case DA is much stronger than prior.
That's a very good summary of Caves' argument, thanks for providing it.
EDIT: I upvoted you, but now I see someone else has downvoted you. As with me, no reason was given.
I am new here at LW. I thought it would be a place for rational discussion. Apparently, however, this is not a universally held belief here.
There's a pretty good level of rational discussion here, better than in most online fora I know of.
Some people are pretty trigger-happy with the downvotes (and some get so worked up over political disagreements that they will go back and downvote many random unrelated comments of yours from the past -- but that's near-universally agreed to be bad and tends to get them banned eventually) but nowhere's perfect. And I think the majority of downvotes are genuinely deserved, though I can't see how anything in this thread deserves them.
Look, some one may say: "A fair coin could fail heads 20 times in row and you will win million dollar". And it is true. But this does not disprove more general statement that: "playing coin for money has zero expected money win".
The same situation is this Caves and DA.
We could imagine situation there DA is wrong, but its is true in most situations (where it is applyable)
See also my large comment about Caves to gjm.
While you didn't make any assumption like this in the post, it's a bit weird to talk about "Doomsday Argument" and "Solutions", as if we know in principle that the argument is wrong and we just have to find out why.
In other words, whether it is right or wrong, there isn't any special reason for the argument to be wrong just because people would like it to be wrong. Trying to get rid of the argument by looking for "solutions" is kind of like going out of your way to look for proofs for the existence of God, just because you want that to be true.
Solution are not only about research if DA is wrong, but about how we should live if it is true.
Personally I think that it is true and the doom is almost inevitable.
We should make some research to prove or disprove DA. The main line of such research would be to try similar to DA logic in other domains, starting from most mundane, like human age, and up to most complex and civilizational level ones.
For example, it is possible to measure size of the Earth using only Copernican mediocracy principle. All we need to know is distance from my birth place to equator, and assumption that human birth places are distributed on randomly distances from equator. I was born 6000 km from equator, and it may be used to conclusion that Earth's radius is around 7000 km which is almost true (real radius is near 6300) Exact calculations here should be more complex, as it must take in account spherical distribution of the observers and will result in bigger (edited) radius.
I think it is an excellent idea to try DA logic in other domains.
Example: A a biologist prepares a petri dish with some nutrients, and implants a small colony of bacteria. The question is: will this colony grow exponentially under these conditions? According to DA logic (with a reference class of all bacteria that will ever live in that petri dish), the biologist does not need to bother doing the experiment, since it is very unlikely that the colony will grow exponentially, because then the current bacteria would be atypical.
To the best of my knowledge, this sort of DA logic is never used by scientists to analyze experiments of this sort (or to decide which experiments to perform). I believe this casts severe doubt on the validity of DA.
Your example is not DA-style, because observer is not self-sampled here. Observer is not bacteria in this experiment. (By the way, most from all existing bacteria is not starters of exponential colonies)
I may suggest another experiment: you tell me your age and I will tell your life expectancy based on DA-logic.
I claim that self-sampling plays no essential role in DA logic.
If you think that self-sampling is essential, then you still must allow one of the bacteria in the petri dish to use DA logic about its own future. If you do not allow the biologist to use DA logic, then the bacterium and the biologist will make different predictions about the likely future. One of them must be more accurate than the other (as revealed by future events). If it is the bacterium that is more accurate, what prevents the biologist from adopting the bacterium's reasoning? I argue that nothing prevents it. And since, in the real world, biologists (and scientists of all fields) do not adopt DA logic, I claim that the most compelling reason for this is the invalidity of DA logic from the get-go.
(I did not downvote you)
Look, we could replace "self sampling" with "random". Random bacteria (from all existing bacteria on Earth) will not start exponential growth. Infinitely small subset of all bacteria will start it. There is no difference between prediction of statistic and biologist in this case. DA is statistical argument. It just say that most of random bacteria will not start exponential growth. The same may be true for young civilizations: most of them will not start exponential growth in the universe. But some may be.
So do you agree with me that, in the experiment I described (a biologist sets up a petri dish with a specific set of initial conditions, and wants to find out if a small bacteria colony will grow exponentially under those conditions), DA logic cannot be applied (by either the biologist or the bacterium) to judge the probable outcome?
DA should be applied to the situation where we know our position in the set, but do not know any other evidence. Of course if we have another source of information about the set size it could overweight DA-logic. If in this experiment the substrate is designed to support bacterial growth, it have is very strong posteriory evidence for future exponential growth.
But if you put random bacteria on random substrate it most likely will not grow. In this case DA works. DA here says that 1 bacteria most likely will have only several off springs, and it is true for most random bacteria on random substrates.
So, will DA works here or not depends of details of the experiment with you did not provide.
OK, let me rephrase the question.
The biologist has never heard of DA. He sets up the initial conditions in such a way that his expectation (based on all his prior knowledge of biology) is that the probability of exponential growth is 50%.
Now the biologist is informed of DA. Should his probability estimate change?
Probably, not, as he has a lot of information about the subject. DA is helpful in case if you don't have any other information about the subject. Also DA is statistical argument thereby it could not be disproved by counterexample. It is always possible to construct a situation where it will not work. Like some molecules in the air are not moving, despite the fact that median velocity is very high.
It may be used in such problems as bus waiting problem (variant of Laplace sunrise problem). If last bus was 5 minutes ago, want is the probability that it will come in next 1 millisecond, next 5 minutes? next 1 year?
At least some DA proponents claim that there should always be a change in the probability estimate, so I am pleased to see that you agree that there are situations where DA conveys no new information.
The situation would change, if I were Adam, first man in the world, and a priory will be able to start exponential human growth with P= 50 per cent probability (or think so). After finding that I am Adam, I would have to update this probability to lower. The way I update depends of sampling method - SSA or SIA but both result in early doom. SSA says that I am in short world. SSI said that my apriory estimation of universal distribution of short and long civilization may be wrong. It would be especially clear if apriory P would not 50 percent, but say 90 per cent.
and assumption that human birth places are distributed on randomly distances from equator.
Which is a pretty silly assumption that happens to be not true in real life.
It's clear that this assumption may be refined in two ways: accounting for spherical geometry and accounting for agriculture conditions, both of which will result in higher density near equator and thus larger Earth radius in this calculation. But if we are interesting to estimate Earth's radius just up to order of magnitude, it will still work.
The main idea was to present another DA-style calculation and check if DA-logic works. It works.
Before accounting for agricultural conditions you probably should account for the distribution of land masses... But anyway, how is this a "DA-style calculation"?
DA-style here means that my position is some set is used to estimate total size of the set, assuming that I random observer from this set. DA-style is also means that we ignore other available information about me, Earth etc, but use only my position in the set to get very rough estimate of total size of the set. The study of such DA-style predictions in known domains could help us estimate validity of DA in unknown domains.
This is probably the wrong place to ask, but I'm confused by one point in the DA.
For reference, here's Wikipedia's current version:
Denoting by N the total number of humans who were ever or will ever be born, the Copernican principle suggests that humans are equally likely (along with the other N − 1 humans) to find themselves at any position n of the total population N, so humans assume that our fractional position f = n/N is uniformly distributed on the interval [0, 1] prior to learning our absolute position.
f is uniformly distributed on (0, 1) even after learning of the absolute position n. That is, for example, there is a 95% chance that f is in the interval (0.05, 1), that is f > 0.05. In other words we could assume that we could be 95% certain that we would be within the last 95% of all the humans ever to be born. If we know our absolute position n, this implies[dubious – discuss] an upper bound for N obtained by rearranging n/N > 0.05 to give N < 20n.
My question is: What is supposed to be special about the interval (0.05, 1)?
If I instead choose the interval (0, 0.95), then I end up 95% certain that I'm within the first 95% of all humans ever to be born. If I choose (0.025, 0.975), then I end up 95% certain that I'm within the middle 95% of all humans ever to be born. If I choose the union of the intervals (0, 0.475) & (0.525, 1), then I end up 95% certain that I'm within the 95% of humans closer to either the beginning or the end.
As far as I can tell, I could have chosen any interval or any union of intervals containing X% of humanity and then reasonably declared myself X% likely to be in that set. And sure enough, I'll be right X% of the time if I make all those claims or a representative sample of them.
I guess another way to put my question is: Is there some reason - other than drama - that makes it special for us to zero in on the final 95% as our hypothesis of interest? And if there isn't a special-making reason, then shouldn't we discount the evidential weight of the DA in proportion to how much we arbitrarily zero in on our hypothesis, thereby canceling out the DA?
Yes, yes, given that there's so much literature on the topic, I'm probably missing some key insight into how the DA works. Please enlighten.
If I instead choose the interval (0, 0.95), then I end up 95% certain that I'm within the first 95% of all humans ever to be born.
What would this imply about the total number of humans? If you knew that you were the 50th percentile human, for example, that would give you the total number of humans, and the same is true for all percentiles.
I think the 'continuous' approach to the DA, which does not rely on the 'naturalness' of 1/20th, goes like the following:
Suppose across all of time there are a finite number of humans, and that we can order them by time of birth.
To normalize the birth orders, we can divide each person's position in the ordering by the total number of people, meaning each person corresponds to a fractile between 0.0 and 1.0.
My prior should be that my fractile is uniformly distributed between 0.0 and 1.0.
Upon observing that I am human number 108 billion, I can now combine this with my prior on the fractile to compute the estimated human population.
There is a 1% chance that my fractile is between 0.99 and 1.0, which would imply there is a 1% chance the total number of humans is between 109B and 108B. (The larger number is earlier because it corresponds to being the 99th percentile human instead of the 100th percentile human.) We now add this up for all possible fractiles, to get a distribution and a mean.
This is a tool for integration. If I'm number N and my fractile is f, then the total number of humans is N/f. So we integrate
, which... does not converge. The expected number of future humans is infinite!
But while the expectation diverges, that doesn't mean the most likely value is infinite humans. The median value is determined by f=0.5, where there are only 108B more humans. In fact, for any finite number of humans, one can calculate the probability that there will be that many or fewer humans--which is why the last 95% of humans is relevant. Those are the ones where the extinction numbers are soonest.
Any real resolution of the Doomsday Argument needs to replace the basic structure of "assume uniform prior on fractile distribution, combine with number of observed humans" with "assume uniform prior on fractile distribution, update fractile distribution based on modeled trajectory of history, combine with number of observed humans." For example, one could look at human history and the future and say "look, extinction in the near future seems very likely, and growth to immense numbers seems very likely, but exactly 100B more humans looks very unlikely. We need to replace our Beta(1,1) distribution with something like a Beta(0.5,0.5) distribution."
As we are interested in future time of humanity existence we choose this interval. If we have different question, we may choose different intervals.