This post was written during the agent foundations fellowship with Alex Altair funded by the LTFF.

Introduction

This is the second part of a two posts series explaining the Internal Model Principle and how it might relate to AI Safety, particularly to Agent Foundations research. In the first post, we constructed a simplified version of IMP that was easier to understand and focused on building intuition about the theorem's assumptions. In this second post, we explain the general version of the theorem as stated by Cai&Wonham^[1] and discuss how it relates to alignment-relevant questions such as agent-structure problem and selection theorems. 

We present the more general setup and explain Feedback and Regulation conditions. With those, we prove a first result. Then, we discuss the meaning of this first result and add another condition called "Observability" to derive another result. After this, we provide a worked out example and discuss possible extensions of the theorem.

Setup

The IMP from Cai&Wonham^[1] originally models the following control theory situation:

Suppose there's, for example, a chemical powerplant in a given environment. The temperature of the plant should be constant and the plant's temperature is affected by the environment's temperature, since they exchange heat, so there is a temperature system made of heaters and air conditioning systems inside the plant, controlled by a controller. This controller controls this systems: it receives information from the environment's temperature and passes a signal to the temperature inside the plant to counter-act the effect of the environment:

• If the environment is hot, air conditionings are turned on.
• If the environment is cold, heaters are turned on.

Naturally, one thing that could happen is that the controller could receive information from the environment and then, after that, control the temperature system. The theorem shows that, under specific circumstances, the controller actually "foresee" the environment's temperature and control the plant temperature concurrently to the environment's temperature changing. We use "foresee" because what the theorem really shows is that, under some circumstances, the controller is autonomous (i.e, it doesn't use outside information to decide how to control the temperature system) and it controls the temperature system in a way that counter-acts the environment's effect (even without using information from the environment). 

In Cai&Wonham's^[1] book, 

"Environment (E), Controller (C) and Plant (P) are dynamic systems which generate, via suitable output maps, the reference, control and output signals respectively. The objective of regulation is to ensure that the output signal coincides (eventually) with the reference, namely the system ‘tracks’. To this end the output is ‘fed back’ and compared (via $\otimes$) to the reference, and the resulting tracking error signal used to ‘drive’ the controller. The latter in turn controls the plant, causing its output to approach the reference, so that the tracking error eventually (perhaps as $t\to \infty$) approaches ‘zero’. Our aim is to show that this setup implies, when suitably formalized, that the controller incorporates a model of the Environment: this statement is the Internal Model Principle."

We model the world as any set $X$. For example, we could consider the whole world as $X=E\times C\times P$, comprised of environment, controller and plant. We assume there's a discrete and deterministic world dynamics $\alpha :X\to X$ that specifies how the world evolves. 

We could also consider $P$ and $C$ as a single joint system called internal system (or just controller), and then we'd have $X=E\times C$ (we're calling $C\times P$ just $C$).

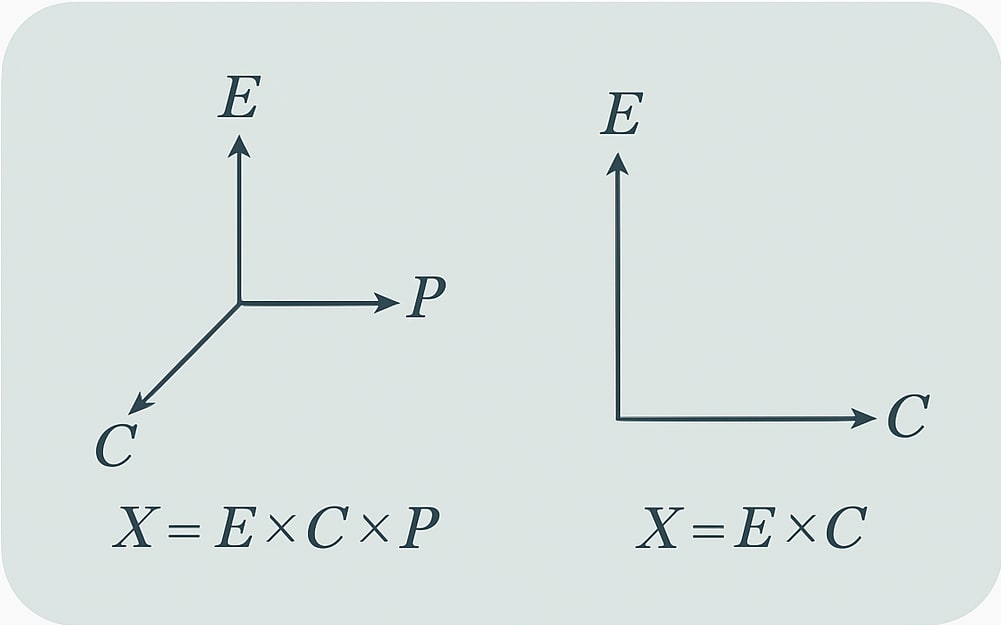
We say a system is autonomous if its next state depends only on the previous state. For example, if $A$ and $B$ are sets, then the function $f:A\to A$ is autonomous and the function $g:A\times B\to A$ is not. We'll just say "A is autonomous" as a slight abuse of terminology. We'll usually write $X_S\subset S$ to denote that $X_S$ is an autonomous system inside $S$ - while $S$ don't need necessarily to be autonomous, for $S=E,C,P$. We assume the environment is autonomous (intuitively, because we can't control the environment, it's a given) with update rule ${\alpha }_E:X_E\to X_E$, where $X_E\subseteq E$. We assume, however, the environment is always autonomous, so $E=X_E$.

We'll denote by $K\subset X$ the set of good states (that is, the set we want our system to be in after a large number of time-steps). It could be, for example, states where the plant's temperature is constant, for any environment state. A important thing to notice is that $K$ is not necessarily the set of states such that the system converges to, because it need not be $\alpha$-invariant - that is, we usually say a system converges to a part of it if it remains in that part after convergence - and it may not be the case that for $x\in K,\alpha \left(x\right)\in K$ - we haven't added any specific condition ensuring that. We don't care about what happened "prior to convergence", so all the states and assumptions we care about will be true on $K$.

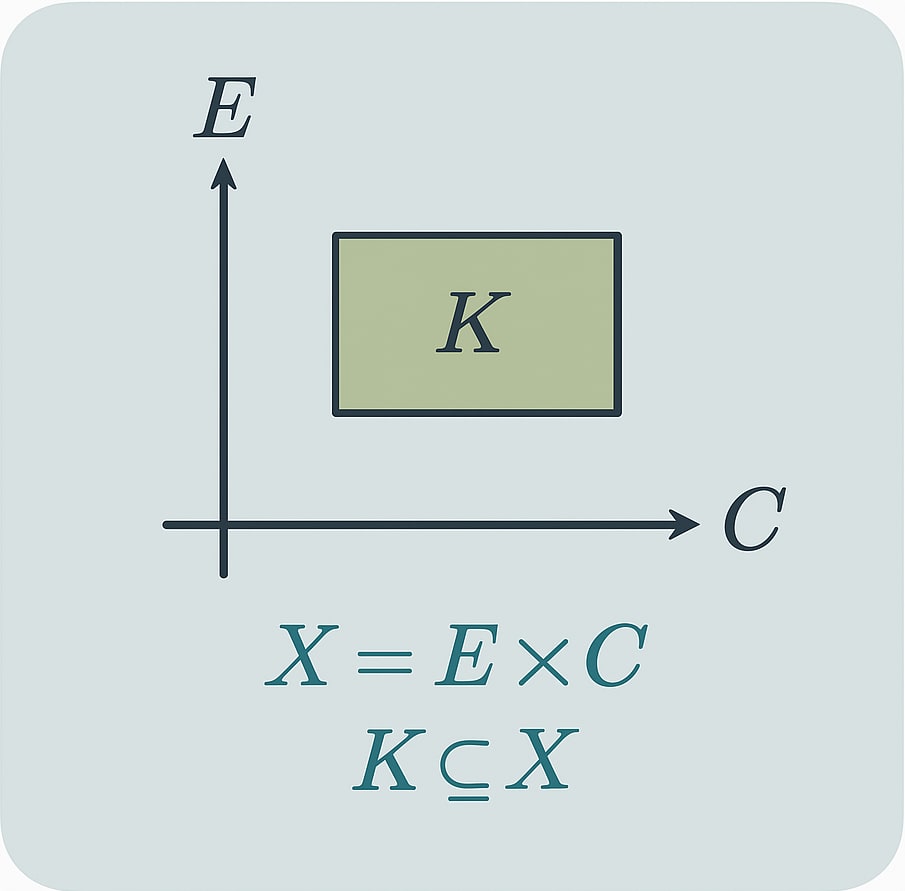
Since $K\subset X$, we can project states out of $K$. For example, if $X=E\times C\times P$, we can write the canonical projection ${\pi }_C:E\times C\times P\to C$ given by ${\pi }_C\left(\right(x_E,x_C,x_P\left)\right)=x_C$. More generally, we could have any function $\gamma :X\to C$ acting as "projection". We define $X_C:=\gamma \left(X\right)\subseteq C$, that is, $X_C$'s elements are controller states that we get from projecting good states to controller states. Recall that earlier we said we would use the "$X_S$" notation to denote autonomous systems, and one of the conclusions of the theorem is that $X_C$ will be autonomous - i.e, we will be able to define a function ${\alpha }_C:X_C\to X_C$ that is also interesting to us. At last, note that, by definition, $\gamma :X\to X_C$ is surjective.

So until now in our setup we have:

• $X$ world, $\alpha :X\to X$
• $X_E$ environment, ${\alpha }_E:X_E\to X_E$
• $K\subseteq X$ set of good states
• $\gamma :X\to X_C$ , $X_C$ denoting all the controller states we're interested in

At this point, the reader might be tempted to ask two things:

1. Ok, the controller states are obtained through the world via a "projection" $\gamma$, but what about the environment states?
2. Is it always true that the environment and world dynamics are consistent with each other? For example, if $X=X_E\times X_C$, it could be that ${\pi }_E\left(\alpha \right(x_E,x_C\left)\right)\ne {\alpha }_E\left({\pi }_E\right(x_E,x_C\left)\right)$

To answer these questions, we'll first play around with the $X=X_E\times X_C$ setup, and then arrive at a property that can be abstractly imposed to other setups.

If  $X=X_E\times X_C$, we have that $X_E={\pi }_E\left(X\right)$. Here, it's not true that $X_E\subseteq X$, but it's obvious that $X_E$ is "a part" of $X$ or "like a subset" of $X$. We want a general property to relate $X_E$ and $X$ such that $X_E$ is "like a subset" of $X$. In mathematics, we use the notion of insertion to work with this. If $A\subset B$, one can trivially define an injection between $A$ and $B$ (the identity, for example). If $A⊈B$, we think of $A$ as "like a subset" of $B$ if one can define an injective function $i:A\to B$. So in general we can just ask for $X_E$ and $X$ to be such that there's an injective function $i_E:X_E\to X$. This partly answers question 1. Now, we'll look closer at insertions to understand if any insertion is allowed. 

(For the following, if you're not familiar with equivalence relations and partitions, go read this section of my first post)

Note that ${\pi }_E:X\to X_E$ is not necessarily invertible, but ${\pi }_E:X\mathrm{mod}\ker {\pi }_E\to X_E$ is a bijection (exercise for the reader), so invertible.

$X\mathrm{mod}\ker {\pi }_E$ is a set containing lines parallel to the $X_E$-axis, so while ${\pi }_E:X\to X_E$ maps points on $X$ to points on $X_E$, ${\pi }_E:X\mathrm{mod}\ker {\pi }_E\to X_E$ maps lines to points on $X_E$. The inverse ${\pi }_E^{-1}:X_E\to X\mathrm{mod}\ker {\pi }_E$ takes a point in $X_E$ and map it to the specific parallel line such that, when projected over $X_E$, it reaches $x_E$. Hence, if we want to define an insertion$i_E:X_E\to X$, we can do the following:

• Given $x_E$, compute ${\pi }_E^{-1}\left(x_E\right)$, this is a line.
• Choose any point in the line and define it to be $i_E\left(x_E\right)$.

By this procedure, if $X_E=R$, for example, we can define an uncountable amount of insertions between $X_E$ and $X$. 

Note, however, that we want the environment to be part of the world, and thus to evolve consistently with the world. For a given $x_E\in X_E$, we have two ways of producing updates of the world now:

1. Compute $i_E\left(x_E\right)\in X$, then compute $\alpha \left(i_E\right(x_E\left)\right)\in X$
2. Compute ${\alpha }_E\left(x_E\right)$, and then $i_E\left({\alpha }_E\right(x_E\left)\right)\in X$

They don't necessarily need to be the same.

Thus, to answer question 1, we ask that $X_E$ and $X$ are such that there's $i_E:X_E\to X$ injective.

To answer question 2, we ask that this injection $i_E$ is such that $i_E\left({\alpha }_E\right(x_E\left)\right)=\alpha \left(i_E\right(x_E\left)\right),\forall x_E\in X_E$.

We define ${\tilde{X}}_E:=i_E\left(X_E\right)$.

Note that, if $X_E\subseteq X$, this is the same as asking $\alpha {|}_{X_E}={\alpha }_E$, so deep down we're asking something related to $X_E$ being $\alpha$-invariant. Indeed, ${\tilde{X}}_E$ is $\alpha$-invariant because:

• if $x\in {\tilde{X}}_E$, then $x=i_E\left(x_E\right)$ and $\alpha \left(x\right)=\alpha \left(i_E\right(x_E\left)\right)=i_E\left({\alpha }_E\right(x_E\left)\right)\in {\tilde{X}}_E$

Assumptions

Feedback Condition

We want to state something that enables us to proof the controller is autonomous and it models the environment. In the first post, we argued that one way to ensure that is by asking the feedback condition:

We want to be able to model a situation where the controller, prior to convergence, needs information from the environment to "learn" how the environment works. Then, after a large number of time-steps, the controller learns the environment's behaviour and becomes autonomous, so instead of asking full feedback, we only ask the controller to be autonomous on good states, that is,

Regulation Condition

We want all environment states to be good states, i.e, to have reached convergence. Since $X_E$ is not necessarily a subset of $X$, we ask 

The Controller Models the Environment

With this assumptions and setup, we're already able to prove the first part of the theorem, that states that the controller models/tracks the environment 

Conclusion (1)

There exists a unique mapping ${\alpha }_C:X_C\to X_C$ determined by ${\alpha }_C\circ \gamma {|}_K=\gamma \circ \alpha {|}_K$

Proof: 

Let $x_C\in X_C$, then $x_C=\gamma \left(x\right)$, for $x\in K$. Define ${\alpha }_C\left(x_C\right)=\gamma \circ \alpha \left(x\right)$. ${\alpha }_C$ is well defined because if $x_C=\gamma \left(x\right)=\gamma \left(x^{\prime }\right)$, then$(x,x^{\prime })\in \ker \gamma {|}_K⟹(x,x^{\prime })\in \ker \gamma \alpha {|}_K⟹\gamma \left(\alpha \right(x\left)\right)=\gamma \left(\alpha \right(x^{\prime }\left)\right)$.

The mapping ${\alpha }_C$ is uniquely determined by ${\alpha }_C\circ \gamma {|}_K=\gamma \circ \alpha {|}_K$: let ${\alpha }_{C,1}$ and ${\alpha }_{C,2}$ satisfying ${\alpha }_{C,i}\circ \gamma {|}_K=\gamma \circ \alpha {|}_K$. Then, for any $x_C=\in X_C,x_C=\gamma \left(x\right)$ for some $x\in K$, since $\gamma$ is surjective and thus ${\alpha }_{C,1}\left(x_C\right)={\alpha }_{C,1}\left(\gamma \right(x\left)\right)=\gamma \left(\alpha \right(x\left)\right)={\alpha }_{C,2}\left(\gamma \right(x\left)\right)={\alpha }_{C,2}\left(x_C\right)$

This point guarantees that we have an autonomous ${\alpha }_C:X_C\to X_C$ and that it

Conclusion (2)

It's true that ${\alpha }_C\circ \gamma {|}_{{\tilde{X}}_E}=\gamma \circ \alpha {|}_{{\tilde{X}}_E}$

Proof: Let $x\in {\tilde{X}}_E$, since ${\tilde{X}}_E\subset K$ by the regulation condition, $x\in K$ and hence ${\alpha }_C\circ \gamma \left(x\right)=\gamma \circ \alpha \left(x\right)=\gamma \circ \alpha {|}_{{\tilde{X}}_E}\left(x\right)$, since $x\in {\tilde{X}}_E$.

Note that if $X_E\subseteq X$, we have $\alpha {|}_{X_E}={\alpha }_E$, so this states that ${\alpha }_C\circ \gamma {|}_{X_E}=\gamma \circ {\alpha }_E$, that is, the controller tracks the environment. For more comments on why ${\alpha }_C\circ \gamma {|}_{X_E}=\gamma \circ {\alpha }_E$ means the controller tracks/models the environment, check out my first post and the section below. 

Note that $\alpha {|}_{{\tilde{X}}_E}$ can be thought of as the environment dynamics inserted into the world.

We say the "internal model" in the controller is the pair consisting of the set $X_M:=\gamma {|}_{{\tilde{X}}_E}\left({\tilde{X}}_E\right)$ and the rule ${\alpha }_C{|}_{X_M}$

In what sense is this a 'model'?

We now digress about the meaning of the theorem above. 

On this session, it's helpful to think that $X_E\subseteq X$, thus ${\alpha }_E=\alpha {|}_{X_E}$. The second conclusion of the theorem is ${\alpha }_C\circ \gamma {|}_{X_E}=\gamma {|}_{X_E}\circ {\alpha }_E$, that is, ${\alpha }_C$ evolves according to ${\alpha }_E$ autonomously: Consider the environment is in state $x_E\in X_E$ at time-step $t$, its next state is ${\alpha }_E\left(x_E\right)$ and the internal system state (which can be calculated via $\gamma$) is $\gamma {|}_{X_E}\left({\alpha }_E\right(x_E\left)\right)$ in time-step $t+1$. On the other hand, $\gamma \left(x_E\right)$ is the system’s state in time-step $t$, and in time-step $t+1$ it is ${\alpha }_C\left(\gamma \right(x_E\left)\right)$. The theorem ensures those two expressions for the internal system’s state in time-step $t+1$ are equal. 

This is qualitatively different from the internal system receiving information about the environment and one time-step later updating to track the environment. The internal system is updating accordingly to the environment in the same time-step. 

To clarify this, consider an analogy of a dog running after a beetle. The dog is initially in the position $d_0$ and the beetle in the position $b_0$. One thing that might happen is that the dog see the beetle's position and starts to move there. When the dog arrives, the beetle already left that position, and is now in a new position. So the dog starts moving to this new beetle position, and when he arrives, the beetle already left again, and so on. 

Another qualitatively different thing that can happen is that the dog actually understands (i.e, "models") how the beetle will move. So instead of moving to the beetle's current position, it moves to where it predicts the beetle will be in the future, so that it can catch it.

The theorem also states ${\alpha }_C$ is unique, so it can’t be the case that there’s other dynamics in a system that satisfies perfect regulation and feedback structure. Hence, the dynamics on the internal model will necessarily be the one that models the environment.

In the dog-beetle analogy, the theorem guarantees that the second scenario will necessarily happen if the dog behavior satisfyies our hypothesis.

The Controller Faithfully Models the Environment

To understand this session better, we recommend the reading of the first post. There, we explain more intuitively the key ideas used here.

In our first post, we were able to prove an analogous result with only feedback structure condition. There, we didn't need to worry about the difference between environment and world and good states. The last theorem is a particular scenario of this post's theorem when we have $X_E=K=X$ and ${\alpha }_E=\alpha {|}_{X_E}$. 

Analogous to the first post, the results proved above includes pathological cases, where, for example, the controller could be $X_C=\{x_{C,1},x_{C,2}\}$ and the environment ${\tilde{X}}_E=N$. Even if we had that ${\alpha }_C\circ \gamma {|}_{{\tilde{X}}_E}=\gamma \circ \alpha {|}_{{\tilde{X}}_E}$, the controller wouldn't have the "expressivity" to faithfully model the environment: it doesn't have enough states to do so. We'll now introduce the observability condition and prove a lemma to conclude the controller faithfully models the environment if, additionally to the prior assumptions, observability is also satisfied. 

Observability can be stated as

For intuition on what does this mean and why we ask this, check out this section of the first post

Generalized Feedback Lemma

We'll prove a generalization of the feedback structure condition in an analogous way we did in the first post, we'll use that together with observability to conclude the controller faithfully models the environment. 

The result we want to prove is

We'll prove it by induction on $k$. 

(Base case): If $k=1$, by feedback condition, we know$\ker \gamma {|}_K\le \ker \gamma \circ \alpha {|}_K$. Since ${\tilde{X}}_E\subseteq K$ by regulation condition, $(x,y)\in \ker \gamma {|}_{{\tilde{X}}_E}⟹(x,y)\in \ker \gamma {|}_K⟹(x,y)\in \ker \gamma \circ \alpha {|}_K$, but since ${\tilde{X}}_E$ is $\alpha$-invariant, and $(x,y)\in {\tilde{X}}_E$, then $\alpha \left(x\right),\alpha \left(y\right)\in {\tilde{X}}_E$, so $(x,y)\in \ker \gamma \circ \alpha {|}_{{\tilde{X}}_E}$. 

(Induction Hypothesis):  Suppose now the theorem holds up until $n$.

 (Inductive step) Let  $x,y\in {\tilde{X}}_E$, then, by definition of kernel of a function, $(x,y)\in \ker \gamma \circ {\alpha }^n{|}_{{\tilde{X}}_E}⟺\left({\alpha }^n\right(x),{\alpha }^n(y\left)\right)\in \ker \gamma {|}_{{\tilde{X}}_E}$ 

Let $s:={\alpha }^n\left(x\right),t:={\alpha }^n\left(y\right)$. Since ${\tilde{X}}_E$ is $\alpha$-invariant, we know $s,t\in {\tilde{X}}_E$. So the equivalence above gives us $(s,t)\in \ker \gamma {|}_{{\tilde{X}}_E}$. By the base case, we have that $\left(\alpha \right(s),\alpha (t\left)\right)\in \ker \gamma \circ \alpha {|}_{{\tilde{X}}_E}$, but $\left(\alpha \right(s),\alpha (t\left)\right)=\left({\alpha }^{n+1}\right(x),{\alpha }^{n+1}(y\left)\right)$, so the result follows by induction. 

Conclusion (3)

$\gamma {|}_{{\tilde{X}}_E}$ is injective

Proof:

1. By generalized feedback lemma, $inf\{\ker \gamma \circ {\alpha }^n{|}_{{\tilde{X}}_E};n=0,1,2,\dots \}=\ker \gamma {|}_{{\tilde{X}}_E}$
2. By observability, $inf\{\ker \gamma \circ {\alpha }^n{|}_K;n=0,1,2,\dots \}=\perp$, but since ${\tilde{X}}_E\subset K$, $\ker \gamma \circ {\alpha }^n{|}_K\le \ker \gamma \circ {\alpha }^n{|}_{{\tilde{X}}_E}$, for any $n$. Hence, $inf\{\ker \gamma \circ {\alpha }^n{|}_{{\tilde{X}}_E};n=0,1,2,\dots \}\le inf\{\ker \gamma \circ {\alpha }^n{|}_K;n=0,1,2,\dots \}=\perp$ 
3. So $\ker \gamma {|}_{{\tilde{X}}_E}=\perp$, so $\gamma {|}_{{\tilde{X}}_E}$ injective

In the next section, we explain why $\gamma {|}_{{\tilde{X}}_E}$  being an injection provides us the meaning of faiyhfully modeling. 

Cardinality and expressivity

In the first post, we concluded $\gamma :X\to X_C$ satisfying the theorem's hypothesis is necessarily a bijection. In terms of cardinality, this means, by definition, that $|X_C|=|X|$. 

In this post, we concluded $\gamma :X_E\to X_C$ injection. In cardinality terms, $|X_E|\le |X_C|$. 

Note that the elements of $X_E$ fully represents the description of each environment state.  Say the environment is the outside of a chemical plant and say the chemical reactions being done there depends on the temperature and pressure of the plant, which in turns depends on the temperature and pressure of the environment. Then, elements $x_E\in X_E$ could be ordered pairs $x_E=(T_E,P_E)$ comprising the external temperature and pressure. On the other hand, if there's an additional relevant environment feature, say, the water delivered from the environment need to be treated (for example, because otherwise the water used in the reactions will be contaminated), one would want to consider an environment state as $x_E=(T_E,P_E,W_E)$, where $W_E$ stands for "quality of water". In other words, $W_E$ is a relevant feature and if we don't include it in the environment, it's as if the environment is not "expressive" enough to model the whole system, and thus even if the theorem applies and the controller of the plant develops an internal model, it could be that it runs poorly, i.e, have bad performance overall (note, though, that we haven't discussed what it means for an internal model to have good performance in reality).

The point here is that the elements of $X_E$ are the only piece of our framework that encompasses the notion of "expressivity".  All the notion of "expressivity" in our setup comes from the sets $X_E$ and $X_C$ (for the controller, you could also say the expressivity comes from $\gamma$, since $X_C$ is determined by $\gamma$, i.e, $\gamma \left(X\right)=X_C$). 

The example above illustrated one way the states can show expressivity, that is, by the structure of the set of states: If $X\subseteq R^{14}$, we perhaps have 14 different relevant features, that could be independent or not. If $X\subseteq N^{10}$, we have 10 features with natural values. 

Another way the states have expressivity is via the state set cardinality, as we talked in the beginning of this section: if $X$ has $|X|=10$ (that is, 10 elements), it can only represent 10 different states.  If $|X|=|N|$, then there's a countable quantity of different states. Recall that cardinality is defined via mappings:

• $f:X\to Y$injection $⟺|X|\le |Y|$
• $f:X\to Y$surjection $⟺|X|\ge |Y|$
• $f:X\to Y$ bijection $⟺|X|=|Y|$

Thus, a state set $X$ exhibits expressivity in two ways:

1. Via $X$'s internal structure
2. Via $X$'s cardinality 

Our theorem states that a necessary condition for the internal system to have an internal model of the environment is $|X_E|\le |X_C|$, that is, in order for the internal system to model the environment, it must exhibit at least as much expressivity as the controller (in the second sense of expressivity). In other words, if the internal system isn't at least as expressive as the environment, the internal system necessarily can't have an internal model of the environment.

Summarizing the whole theorem-meaning discussion, 

• The semantics of the world "model" in the theorem means faithfully tracking/simulating. That is, for states in ${\tilde{X}}_E$ (which the internal system views as $X_M$) the internal system doesn't wait for the environment and then update a timestep later following the environment. Instead, it updates accordingly to the environment in the same time step. We’ll discuss more about that in a later section
• Conclusion (1) guarantees ${\alpha }_C$ - the autonomous dynamics on the controller - is well defined and unique. Conclusion (2) states that ${\alpha }_C$ simulates ${\alpha }_E$ and Conclusion (3) says this simulation is faithful.

Comparing the less general version of the theorem in the first post with this version, 

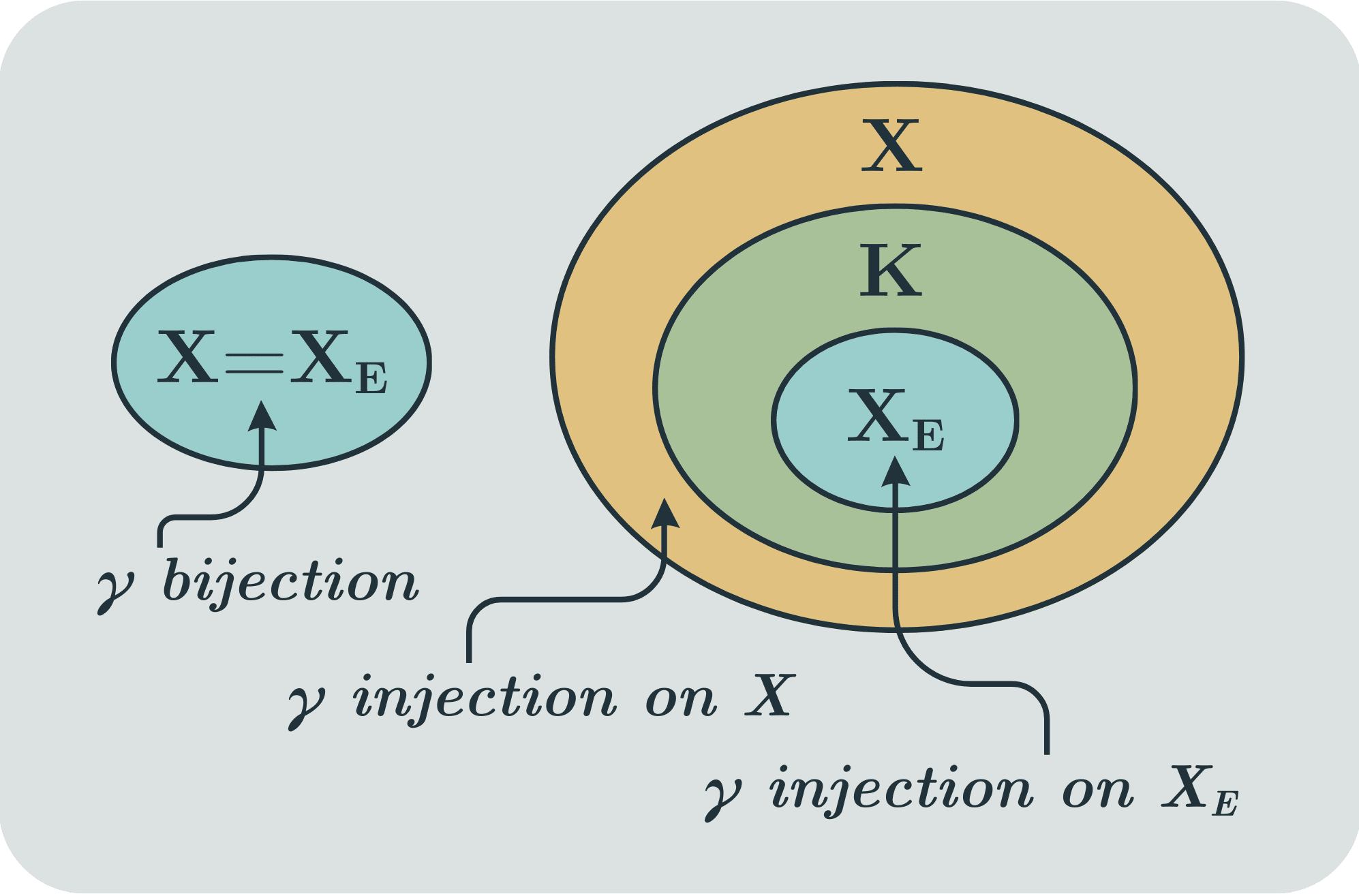
• This theorem does apply for systems where $\gamma$ is not a bijection. In fact, $\gamma$ is injective on $X_E$ and surjective on $K$. It also seems useful to model a wider range of systems.
• Our previous version of the theorem is a particular case of this, with $X_E=X=K$ and ${\alpha }_E=\alpha$.
• ${\tilde{X}}_E\subseteq K$ and $X_C\subseteq \gamma \left(K\right)$ are the conditions ensuring all the states involved in the internal modeling are good states. Thus, this theorem is supposed to apply after the regulation has "converged" in some sense (such as $t\to \infty$).

Thus, modeling here means tracking faithfully.

Example

Consider an unidimensional circular grid of size $N$ (i.e, a row of $N$ squares such that the first square is connected to the last square) with a moving target and an agent that has the goal to pursue that target. The target and the agent can move left and right and are always inside some square of the grid. 

The squares of our grid will be the set $N:=\{0,\dots ,N-1\}$.

We want the world to be able to describe the agent and the moving target, each moving in this $N$ sized grid, so we will consider a state of the world as an ordered pair $(i,j)$ with $i,j\in \{0,\dots ,N-1\}=N$ and so we'll define the world as $X:=N\times N$. Here, the first coordinate of the pair represents the position of the moving target and the second coordinate represents the position of the agent.

We will consider the environment to be the position of the moving target on the grid, thus $X_E:=N$.

We assume the moving target always moves one square to the right. That is, ${\alpha }_E:X_E\to X_E$ is given by ${\alpha }_E\left(i\right):=i+1\mathrm{mod}N$, where the $\mathrm{mod}N$ is to account for the fact that the world is circular.

We'll define the dynamics of the world $\alpha :X\to X$ by $\alpha (i,j)=(i+1\mathrm{mod}N,j+1\mathrm{mod}N)$ if $i=j$ and $\alpha (i,j)=(i+1\mathrm{mod}N,j\mathrm{mod}N)$ if $i\ne j$

Consider $j_E:X_E\to X$ defined by $j_E\left(x_E\right):=(x_E,x_E)$. Then, ${\tilde{X}}_E:=j_E\left(X_E\right)\subseteq X$ and$j_E\circ {\alpha }_E\left(x_E\right)=j_E\left({\alpha }_E\right(x_E\left)\right)=j_E(x_E+1\mathrm{mod}N)=(x_E+1\mathrm{mod}N,x_E+1\mathrm{mod}N)=\alpha \left(\right(x_E,x_E\left)\right)=\alpha \left(j_E\right(x_E\left)\right)=\alpha \circ j_E$

In other words, let ${\alpha }_{{\tilde{X}}_E}:=j_E\circ {\alpha }_E=\alpha \circ j_E=\alpha {|}_{{\tilde{X}}_E}$ (since $j_E$ is injective). Thus we can use the internal model theorem with ${\tilde{X}}_E=j_E\left(X_E\right)$ as environment instead of $X_E$ directly.

For the agent, 

• $X_C$ should represent the states the agent can be in, hence $X_C:=\{0,\dots ,N-1\}$
• $\gamma :X\to X_C$ defined by
  • Clearly, $\gamma$ is a surjection: given $j\in X_C,\exists x=(i,j)\in X$ s.t. $\gamma \left(x\right)=x_C,\forall i\in \{0,\dots ,N-1\}$
• We want our agent to pursue the moving target, so we will define $K:=\left\{\right(i,j)\in X|i=j\}$

This setup satisfy our hypothesis:

• ${\tilde{X}}_E=\left\{\right(x_E,x_E)\in X|x_E\in X_E\}\subseteq K=\left\{\right(i,j)\in X|i=j\}$ and ${\alpha }_{{\tilde{X}}_E}=\alpha {|}_{{\tilde{X}}_E}$
• $\gamma \left(K\right)=N=X_C$
• $\ker \gamma {|}_K\le \ker \gamma \circ \alpha {|}_K$.
  • Suppose $x,y\in K$ such that $(x,y)\in \ker \gamma ⟺\gamma \left(x\right)=\gamma \left(y\right)$. Since $x,y\in K,x=(i,i)$ and $y=(j,j)$. Then, $i=\gamma \left(x\right)=\gamma \left(y\right)=j⟹i=j$. Now, $\gamma \circ \alpha (i,i)=\gamma \circ \alpha (j,j)$ since $i=j$. Thus, $(x,y)\in \ker \gamma \circ \alpha$.
• ${\tilde{X}}_E$ is $\alpha$-invariant.
  • Let $(x_E,x_E)\in {\tilde{X}}_E$, then $\alpha \left(\right(x_E,x_E\left)\right)=(x_E+1\mathrm{mod}N,x_E+1\mathrm{mod}N)=j_E(x_E+1)$ if $x_E+1\le N-1$ and $=j_E\left(0\right)\text{if}{x}_E+1=N$. That is, $\alpha \left(\right(x_E,x_E\left)\right)=j_E\left(x_E^{\prime }\right)\in {\tilde{X}}_E$ for some $x_E^{\prime }\in X_E$.   
• $inf\ker \gamma \circ {\alpha }^n{|}_{{\tilde{X}}_E}=\perp$
  • This follows from feedback and regulation and $\alpha$-invariance of ${\tilde{X}}_E$: Since feedback holds and ${\tilde{X}}_E\subseteq K$, then $\ker \gamma {|}_{{\tilde{X}}_E}\le \ker \gamma \circ \alpha {|}_{{\tilde{X}}_E}$. Because ${\tilde{X}}_E$ is $\alpha$-invariant, one can prove the generalized feedback lemma for the sequence $\ker \gamma \circ {\alpha }^n{|}_{{\tilde{X}}_E}$. Then $inf\ker \gamma \circ {\alpha }^n{|}_{{\tilde{X}}_E}=\perp$

Since the theorem's assumptions are all true, we already know that there's a unique ${\alpha }_C$ determined by ${\alpha }_C\circ \gamma =\gamma \circ \alpha$.

• That is, $x_C=\gamma \left(x\right)=\gamma \left(\right(i,j\left)\right)=j$, ${\alpha }_C\left(x_C\right)=\gamma \left(\alpha \right(x\left)\right)=\gamma \left(\alpha \right(i,j\left)\right)$ $=$ $j\mathrm{mod}N$ if $i\ne j$ and $=j+1\mathrm{mod}N$ if $i=j$. 

Then the pair $X_M=\gamma {|}_{{\tilde{X}}_E}\left({\tilde{X}}_E\right)$ and ${\alpha }_C{|}_{X_M}$ is our internal model.

Discussion and further work

We presented the Internal Model Theorem statement, which basically states that, under a setup of an external system passing signals to an autonomous internal system syuch that these signals satisfy observability, then: feedback structure and regulation implies the controller necessarily have an internal model of the external system.

Some critiques:

• As we discuss in the first post, the update rules involved are all deterministic. Thus, the theorem can't represent non-deterministic scenarios such as taking decisions under uncertainty
  • Note, though, that the theorem is supposed to model regulation after some sort of equilibria or convergence. I expect intuitively many systems in these situations have at least an approximately deterministic behavior
• It's really hard to come up with non-trivial examples for the theorem. This difficulty is particularly present when trying to come up with examples that satisfy Feedback and Observability together
  • In fact, I'd be glad to see non-trivial examples of this theorem. If you know or construct one, please write in the comments or send it

IMP as a selection theorem

A selection theorem is a theorem that states something in the lines of "this is the type of agents we expect to find in environments with this specific type of selection pressure. Currently, the theorem doesn't say much because the controller is not properly an agent. It's an autonomous system, but it doesn't act on the world. Phrased as a selection theorem wannabe, the IMP states that in environments where the controller is autonomous in good states, the controller acts as/tracks the environment internal model. 

We can think of extending the theorem in two directions

•  “Systems that approximately regulate their internal state have approximate internal models”, we would get a better version of a selection theorem.
  • I’d expect this extended theorem to work for a wider range of real world systems.
  • This still wouldn't make the controller look more agentic because it still wouldn't properly act on the world.
• "The controller acts upon the environment but it has an internal model of the environment."
  • This would make the controller more agentic.

The first point above would make the theorem more useful to real systems, while the last would make the controller feel more like an agent. I'd think those two extensions would provide a selection theorem.

Relevance to Agent Structure problem

The agent-like structure problem is the problem of determining if, given a policy that robustly optimizes far away regions of the space into small chunks of the state space, does this policy has agent structure (by agent structure we mean informally having an internal model and a search process)? Another way to phrase this questions is "under which types of environments is the implication above true?"

Alex gave a loose formalism to answer this question, making some notions more precise:

"If we take some class of behaving things and apply a filter for agent-like behavior, do we end up selecting things with agent-like architecture (or structure)? Under which conditions does agent-like behavior imply agent-like structure?"

This loose formalism consist of a policy and an environment. The policy receives an observation from the environment, updates its internal state and acts on the environment, changing its state. Then the environment sends a new observation to the policy and so on, in discrete time-steps. The policy is, thus, a function that sends each policy state and observation to a policy state. Analogously, the environment sends each environment state and action to an environment state.

We can define a class of different policies and different environments. 

The idea of the formalism is being able to assess a function that associates to each policy in the policy class a number in $[0,1]$, thought of as the "degree of agent structure". We expect policies that perform well in a wide range of environments are highly “agentic”. Based on the performance of a policy in a wide range of environments, we want to be able to tell the degree of agent structure this policy has. 

In Alex's words, 

“One result we might wish to have is that if you tell me how many parameters are in your ML model, how long you ran it for, and what its performance was, then I could tell you the minimum amount of agent structure it must have”.

The important idea here is that we expect to be able to define a function $ϵ$ depending on the parameters, training, performance or other relevant variable such that it’s always true that the structure of a given policy is $\ge 1-ϵ$. Since we want the structure function to be between $0$ and $1$, $ϵ=1$ would always make this statement true, but we want this function to be zero in the limit, in some sense of limit.

More concretely, in the agent structure setup, we want to be able to:

1. Have a measure of performance of a given policy in a wide range of environments.
2. Filter the policy class (because a lookup table containing “optimal” moves for each environment in the environment class would have a very good performance, but we would expect a lookup table would be the policy with less agent structure amongst all policies).
3. Define $ϵ$ appropriately such that its limit is zero in some sense of asymptotics.

The IMP setup fails these conditions because

1. It doesn’t encompass a measure of performance of different policies. Actually, we’ve already proved the dynamics of the internal system is unique under IMP conditions, so we would actually have only one policy.
2. The IMP’s setup doesn’t seem to consider a policy acting over an environment. The internal system (the analogous of policy here) can be influenced by the environment (via $\gamma$), but can’t influence the environment. In a self-driving car analogy, it’s like the car being in position $x=10$ or $x=20$, moving or not corresponds to same environment states. 

We wish to extend the IMP in two different ways, addressing those two problems:

1. Modify the IMP to show that systems which approximately regulate their internal state must have approximate models of their environments.
   1. This could give us a notion of performance and different policies.
2. Rework the IMP so that it applies to controllers regulating the external environment (rather than regulating their internal state).
   1. This would solve the fact that in current IMP, the internal system doesn’t interact with the environment.

We expect if one can extend the theorem to these two different situations, it might give some insight on the agent structure problem.

1. ^{^}

   Supervisory Control of Discrete-Event Systems, (2019) Cai & Wonham as section 1.5.