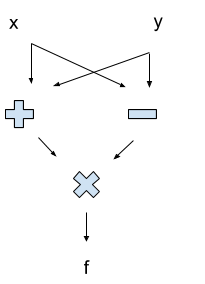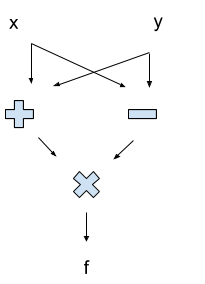Crossposted here.
Directed acyclic graphs (DAGs) turn out to be really fundamental to our world. This post is just a bunch of neat stuff you can do with them.
Utility Functions
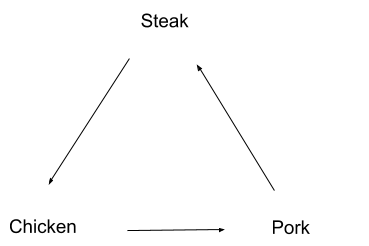
Suppose I prefer chicken over steak, steak over pork, and pork over chicken. We can represent my preferences with a directed graph like this:
This poses a problem. If I’m holding a steak, then I’ll pay a penny to upgrade it to chicken — since I prefer chicken over steak. But then I’ll pay another penny to upgrade my chicken to pork, and another to upgrade it to steak, and then we’re back to the beginning and I’ll pay to upgrade the steak to chicken again! Someone can stand there switching out chicken/pork/steak with me, and collect my money all day.
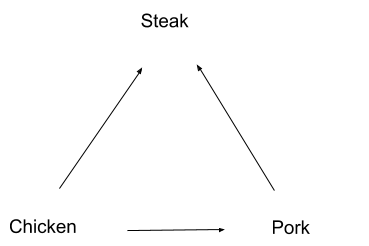
Any time our preference graph contains cycles, we risk this sort of “money-pump”. So, to avoid being money-pumped, let’s make our preferences not contain any cycles:
Now our preferences are directed (the arrows), acyclic (no cycles), and a graph (arrow-and-box drawing above). It’s a DAG!
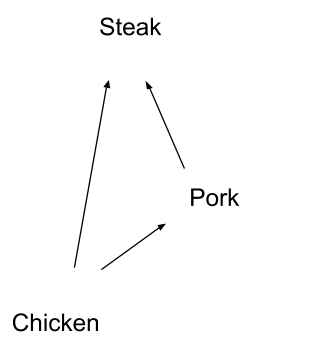
Notice that we can now sort the DAG nodes, spatially, so that each node only points to higher-up nodes:
Reading off the nodes from bottom to top, the order is: chicken, pork, steak.
This is called a topological sort, or topo sort for short. We can always topo sort a DAG — there is always some order of the nodes such that each node only points to nodes after it in the sort order.
In this case, the topo sort orders our preferences. We prefer pork over everything which comes before pork in the topo sort, and so forth. We could even number the items according to their topo-sorted order: 1 for chicken, 2 for pork, 3 for steak. We prefer whichever thing has the higher number, i.e. the higher position in the topo-sort order.
This is called a utility function. This utility function U is defined by U(chicken) = 1, U(pork) = 2, U(steak) = 3. We prefer things with higher utility — in other words, we want to maximize the utility function!
To summarize: if our preferences do contain cycles, we can be money-pumped. If they don’t, then our preferences form a DAG, so we can topo sort to find a utility function.
Circuits
Here’s a really simple circuit to compute f = (x+y)*(x-y):
Notice that the circuit is a DAG. In this case, the topo sort tells us the order in which things are computed: “+” and “-” both come before “x” (the multiplication, not the input). If the graph contained any cycles, then we wouldn’t know how to evaluate it — if the value of some node changed as we went around a cycle, we might get stuck updating in circles indefinitely!
It’s the DAG structure that makes a circuit nice to work with: we can evaluate things in order, and we only need to evaluate each node once.
Dynamic Programming
Here’s a classic algorithms problem:
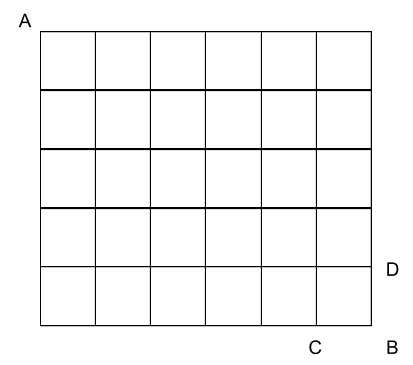
Suppose we want to compute the number of paths from corner A to corner B, travelling only down and right along the lines. (I’m about to give a solution, so pause to think if you don’t want to be spoilered.)
Our main trick is that the number of paths to B is the number of paths to C plus the number of paths to D. Likewise, for any other node, the number of paths to the node is the sum of the numbers above and to the left. So we can turn the picture above into a circuit, by sticking “+” operations at each node and filling in the arrowheads:
I’ve omitted all the tiny “+” signs, but each node in this circuit sums the values from the incoming arrows. Start with 1 at corner A (there is only one path from A to itself), and the circuit will output the number of paths from A to B at corner B.
Why is this interesting? Well, consider coding this up. We can make a simple recurrent function:
f(row, col):
if row == 0 or col == 0:
return 1
return f(row-1, col) + f(row, col-1)
… but this function is extremely inefficient. In effect, it starts at B, then works backward toward A, exploring every possible path through the grid and adding them all up. The total runtime will be exponential in the size of the grid.
However, note that there are not that many combinations of (row, col) at which f will be evaluated — indeed, there’s only one (row, col) combination for each node in the grid. The inefficiency is because our simple recurrent function calls f(row, col) multiple times for each node, and runs the full computation each time. Instead, we could just compute f for each node once.
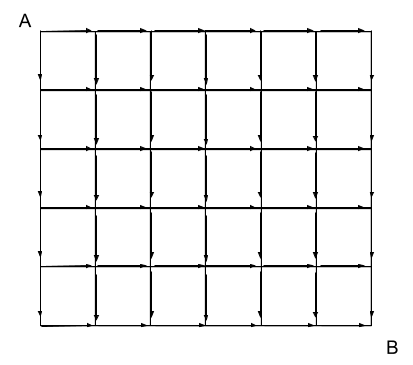
How can we do that? We already did! We just need to treat the problem as a circuit. Remember, when evaluating a circuit, we work in topo-sorted order. In this case, that means starting from A, which means starting from f(0,0). Then we store that value somewhere, and move on — working along the top f(0, col) and the side f(row, 0). In general, we work from upper left to lower right, following topo sort order, and storing results as we go. Rather than using function calls, as in the recursive formulation, we just lookup stored values. As long as we follow topo sort order, each value we need will be stored before we need it.
This is “dynamic programming”, or DP: taking a recursive function, and turning it into a circuit. Traditionally, DP is taught with tables, but I find this deeply confusing — the key to DP is that it isn’t really about tables, it’s about DAGs. We take the computational DAG of some recursive function, and turn it into a circuit. By evaluating in topo-sort order, we avoid re-evaluating the function at the same node twice.
Turing-Computable Functions: Circuits + Symmetry
To turn circuits into fully general Turing-computable functions (i.e. anything which can be written in a programming language), we just need to allow recursion.
Here’s a recursive factorial function:
f(n):
if n == 0:
return 1
return n * f(n-1)
We can represent this as an infinite circuit:
Each of the dashed boxes corresponds to a copy of the function f. The infinite ladder handles the recursion — when f calls itself, we move down into another box. We can view this as a symmetry relation: the full circuit is equivalent to the top box, plus a copy of the full circuit pasted right below the top box.
Of course, if we actually run the code for f, it won’t run forever — we won’t evaluate the whole infinite circuit! Because of the conditional “n == 0?”, the behavior of the circuit below some box is irrelevant to the final value, so we don’t need to evaluate the whole thing. But we will evaluate some subset of the circuit. For n = 2, we would evaluate this part of the circuit:
This is the “computational DAG” for f(2). While the code for f defines the function, the computational DAG shows the computation — which steps are actually performed, in what order, with what dependencies.
Parallelization
The computational DAG forms the basis for parallelization: speeding up an algorithm by running on multiple cores at once.
Consider our simple circuit from earlier:
Where can we perform steps in parallel? Well, we can evaluate the “-” and “+” at the same time. But we can’t perform the “x” until after both the “-” and “+” are done: the “x” requires the results from those two steps.
More generally, look at the topo sort order of the circuit. The topo sort is not unique — “+” could come before or after “-”, since there’s no directed path between them. That means they can be performed in parallel: neither requires the result from the other. On the other hand, “x” comes strictly later in the topo sort order, because it does require the other values as input.
For a more complicated function, we’d have to think about the computational DAG. Whenever one node comes strictly after another in the computational DAG, those two nodes cannot be parallelized. But as long as neither node comes strictly after the other, we can parallelize them. For instance, in our DP example above, the points C and D in the grid could be evaluated in parallel.
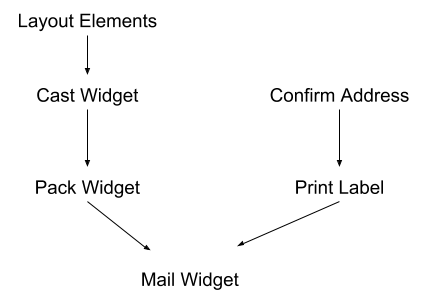
This sort of thinking isn’t restricted to computer science. Suppose we have a company producing custom mail-order widgets, and every time an order comes in, there’s a bunch of steps to crank out the widget:
Some steps depend on others, but some don’t. We can confirm the address and print the label in parallel to producing the widget itself, in order to mail it out sooner. A lot of optimization in real-world company processes looks like this.
Causality
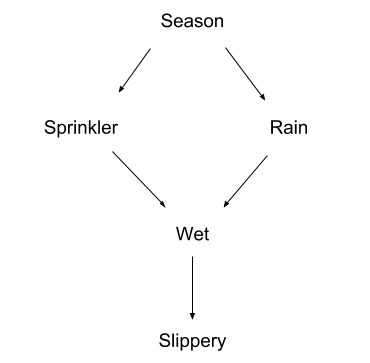
Here’s a classic example from Pearl:
The season could cause rain, or it could cause you to run the sprinkler, but the season will not directly cause the sidewalk to be wet. The sidewalk will be wet in some seasons more than others, but that goes away once you control for rain and sprinkler usage. Similarly, rain can cause the sidewalk to be wet, which causes it to be slippery. But if something keeps the sidewalk dry — a covering, for instance — then it won’t be slippery no matter how much it rains; therefore rain does not directly cause slipperiness.
These are the sort of common-sense conclusions we can encode in a causal DAG. The DAG’s arrows show direct cause-effect relations, and paths of arrows show indirect cause and effect.
A few of the neat things we can do with a causal DAG:
- Mathematically reason about how external changes (e.g. covering a sidewalk) will impact cause-effect systems
- Account for causality when updating beliefs. For instance, a wet sidewalk makes rain more likely, but not if we know the sprinkler ran.
- Find a compact representation for the probability distribution of the variables in the DAG
- Statistically test whether some data is compatible with a particular causal DAG
Most of these are outside the scope of this post, but Highly Advanced Epistemology 101 has more.
The DAG structure of causality is the main reason for the ubiquity of DAGs: causality is everywhere, so DAGs are everywhere. Circuits are really just cause-effect specifications for calculations. Not utility, though — that one’s kind of an outlier.