I'm curious about your sense of the path towards AI safety applications, if you have a more specific and/or opinionated view than the conclusion/discussion section.
My main opinionated view relative to current discourse is that if someone is trying to apply any of this directly to LLMs, then they are probably very deeply confused about natural abstractions and also language and also agency/intelligence/etc in general.
The path we're optimizing for right now is to figure out the whole damn core of the theory of agency, get it across the theory-practice gap, and then not be so clueless about everything. See The Plan. Possibly with AI acceleration of the research at some point; our decisions right now are basically the same regardless of whether the research will be accelerated by AI later.
Just skimmed for now...
We say a latent is a "redund" over observables if and only if is fully determined by each individually, i.e. there exist functions such that for each . In the approximate case, we weaken this condition to say that the entropy for all , for some approximation error .
I see your latest result has allowed you to streamline the definitions of redundancy and redunds.
I think attempting to require to be small in terms of would still run into my counterexample, right? (Setups could be constructed such that requiring to be -small would cause to scale arbitrarily with , and vice versa. So in the general case, there may exist valid redunds with the redundancy error such that the maximal redund's and (and therefore ) cannot both be -small.)
(Mediation)
Wait, so it's enough for the agents to just believe the observables are independent given the state of their latents? We only need the to be independent conditional on under a particular model ?
I didn't realise that. I thought the observables had to be 'actually independent' after conditioning in some sort of frequentist sense.
Getting a version of this that works under approximate Agreement on Observables sounds like it would be very powerful then. It'd mean that even if Alice is much smarter than Bob, with her model e.g. having more FLOP which she can use to squeeze more bits of information out of the data, there'd still need to be a mapping between the concepts Bob and Alice internally use in those domains where Bob doesn't do very much worse than Alice on predictive accuracy.
So, if a superintelligence isn't that much better than humanity at modelling some specific part of reality, there'd need to be an approximate mapping between humanity's latents and (some of) the superintelligence's latents for that part of reality. If the the theorems approximately hold under approximate agreement on observables.
Yup, that is correct.
If the the theorems approximately hold under approximate agreement on observables.
Yeah, there is still the issue that the theorems aren't always robust to approximation on the Agreement on Observables condition, though the Solomonoff version is and there's probably other ways to sidestep the issue.
I think a subtle point is that this is saying we merely have to assume predictive agreement of distributions marginalized over the latent variables , but once we assume that & the naturality conditions, then even as each agent receive more information about to update their distributions & latent variables , the deterministic constraints between the latents will continue to hold.
Or if a human and AI start out with predictive agreement over some future observables, & the AI's latent satisfy mediation while human's latent satisfy redundancy, then we could send the AI out to update on information about those future observables, and humans can (in principle) estimate the redundant latent variable they care about from the AI's latent without observing the observables themselves. The remaining challenge is that humans often care about things that are not approximately deterministic w.r.t observables from typical sensors.
Yes, though I'll flag that we don't have robustness with respect to approximation on the agreement condition (though we do have other ways around that to some extent, e.g. using the Solomonoff version of natural latents), and those sorts of updates are the kind of thing which I'd expect to run into that robustness problem.
Which formal properties of the KL-divergence do the proofs of your result use? It could be useful to make them all explicit to help generalize to other divergences or metrics between probability distributions.
The appendices make heavy use of additivity across independent variables (and across factorizations more generally), which is the main thing I'd expect to need to work around in order to use other divergences/metrics.
Really gorgeous stuff with philosophically significant and plausibly practical implications. Great work. I assume you've also looked at this from a categorial perspective? It would surprise me if treating latents as limits didn't simplify some of the arguments (or at least the presentation, which is already admirably clear). And I can't help but wonder whether "bigger" uniqueness/isomorphism/stability results for world-models or other features of agents might result from comparing Bayes net categories. If you haven't tried categorial abstractions (I dunno the specifics---there are a few categorification choices that I could see being useful here), play around with them.
Graphical statement of Theorem 2
I find this picture pretty misleading, because it seems to say that if is determined by , then is a mediator, when really this is false, and it's stated explicitly in the text above that Alice's latent satisfying mediation is assumed.
I think you might have misread something? The graphical statement of theorem 2 does not say that if is determined by , then is a mediator; that would indeed be false in general. It says that:
- If is a mediator and we have agreement on observables, then...
- ... naturality of implies that is determined by .
In particular, the theorem says that under some conditions is determined by . Determination is in the conclusion, not the premises. On the flip side, being a mediator is in the premises, not the conclusion.
This was all clear to me, but only from reading the text; my comment is just to say that the graphical statement doesn't show being a mediator in the premises, so in isolation it gives the wrong idea; this led to a little confusion.
To be clear, I am talking about the reverse direction, as pictured here:
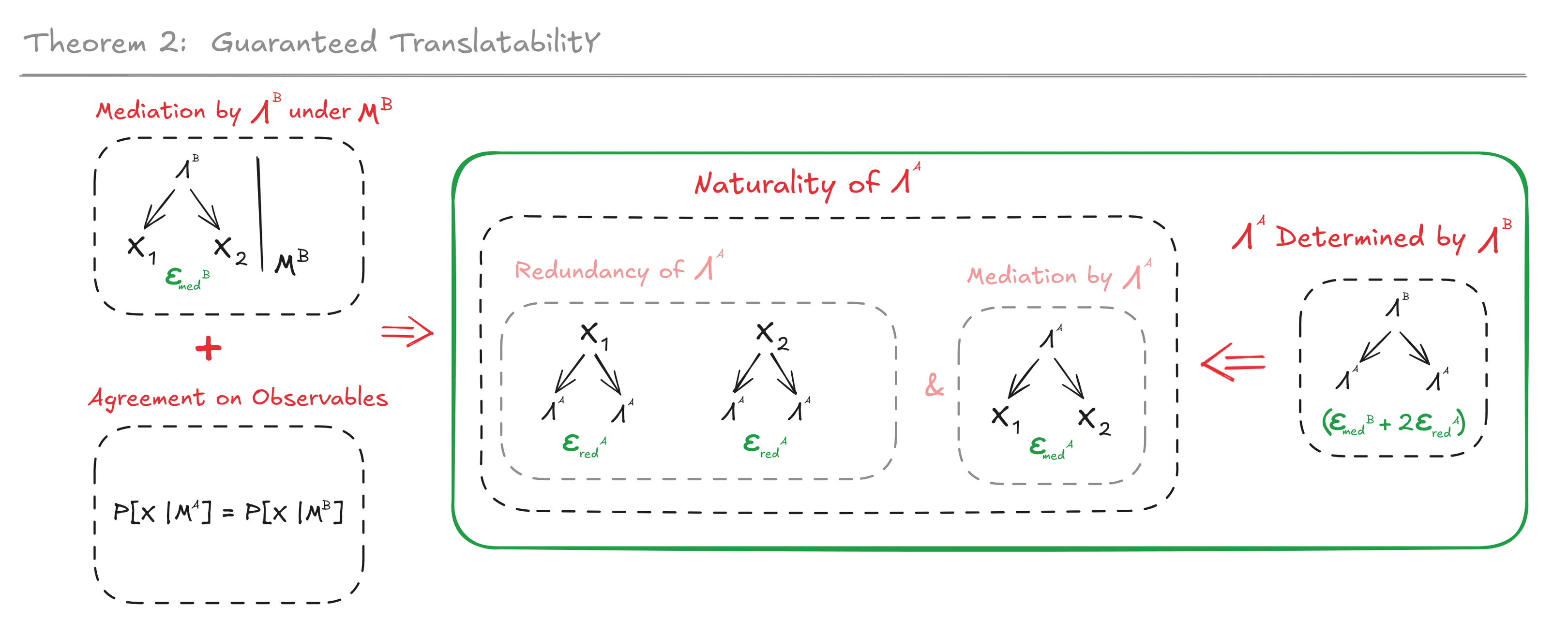
I understand that you have already set up as a mediator immediately above the image. Your text is perfectly clear:
In other words, we want to show: if Alice' latent satisfies Mediation, and for any latent Bob could choose (i.e. any other mediator) we have , then Alice' latent must be natural.
Great work! I have a technical question.
My current understanding is as follows:
1. If we have even one observable variable with agreement observation and for which the latent variables satisfy the exact naturality condition, we can then build the transferability function exactly.
2. In the approximation case, if we have multiple observable variables that meet these same conditions, we can choose the specific variable (or set of variables, in the proofs you used a couple) that will minimize the errors. We would not need to use all of them.
Is this correct?
Additionally, I was wondering if you have attempted to implement the algorithm derived from the proof to construct the isomorphism. It seems that some effort could be dedicated to developing an algorithm that minimizes or reduces these errors. It could one day be helpful for interpreting and aligning different ontological frameworks, like mapping an alien Bayesian network to a human one.
I do not understand the statement of your current understanding, in particular point 1. Could you please state in different words and/or state it formally and/or give an example?
By scanning the graphical proof, I don't see any issue on the following generalization of the Mediator Determines Redund Theorem:
Let and be random variables and let be any not-empty subset of that satisfy the following conditions:
- Mediation: are independent given
- Redundancy:
Then .
In the above, I've weaken the Redundancy hypothesis, requiring that the redundancy of any subset of random variables is enough to conclude the thesis.
Does the above generalization work (if don't, why?).
If the above stands true, then just one observational random variable (with agreement) is enough to satisfy the Redundancy condition (Mediation is trivially true with one variable), an therefore is determined by Moreover, in the general approximation case, if we have various sets of random variables that meet the naturality condition, we can choose the one that will minimize the errors (there's some kind of trade-off between and errors).
Ah, yes, that is almost correct. You need redundancy over TWO distinct observables (i.e. the subset must be at least size two), not just one, but otherwise yes. With just one observable, you don't have two branches to dangle a off of in the graphical proof, so we can't get between two copies of .
Background on where this post/paper came from
About a year ago, we wrote up a paper on natural latents for the ILLIAD proceedings. It was mediocre. The main shortcoming stemmed from using stochastic rather than deterministic natural latents, which give much less conceptually satisfying ontological stability guarantees; there was this ugly and confusing caveat on everything throughout the paper. We knew at the time that deterministic natural latents gave a much cleaner story, but we were more concerned about maintaining enough generality for our results to bind to reality than about getting the cleanest story.
Recently, we proved that existence of a stochastic natural latent implies existence of a deterministic natural latent (specifically under approximation; the exact case is easy). So now, we can write the paper the way we'd really like, without sacrificing generality.
This post is an overhaul of (and large improvement to) a paper we wrote about a year ago. The pdf version is available on arXiv here. As of posting, this is probably the best first-stop mathematical intro to natural latents.
Abstract
Suppose two Bayesian agents each learn a generative model of the same environment. We will assume the two have converged on the predictive distribution (i.e. distribution over some observables in the environment), but may have different generative models containing different latent variables. Under what conditions can one agent guarantee that their latents are a function of the other agent’s
latents?
We give simple conditions under which such translation is guaranteed to be possible: the natural latent conditions. We also show that, absent further constraints, these are the most general conditions under which translatability is guaranteed. Crucially for practical application, our theorems are robust to approximation error in the natural latent conditions.
Background
When is robust translation possible at all, between agents with potentially different internal concepts, like e.g. humans and AI, or humans from different cultures? Under what conditions are scientific concepts guaranteed to carry over to the ontologies of new theories, (e.g. as general relativity reduces to Newtonian gravity in the appropriate limit?) When and how can choices about which concepts to use in creating a scientific model be rigorously justified, like e.g. factor models in psychology? When and why might a wide variety of minds in the same environment converge to use (approximately) the same concept internally?
These sorts of questions all run into a problem of indeterminacy, as popularized by Quine[1]: Different models can make exactly the same falsifiable predictions about the world, yet use radically different internal structures.
On the other hand, in practice we see that
Combining those, we see ample empirical evidence of a high degree of convergence of internal concepts between different humans, between humans and AI, and between different AI systems. So in practice, it seems like convergence of internal concepts is not only possible, but in fact the default outcome to at least a large extent.
Yet despite the ubiquitous convergence of concepts in practice, we lack the mathematical foundations to provide robust guarantees of convergence. What properties might a scientist aim for in their models, to ensure that their models are compatible with as-yet-unknown future paradigms? What properties might an AI require in its internal concepts, to guarantee faithful translatability to or from humans' concepts?
In this paper, we'll present a mathematical foundation for addressing such questions.
The Math
Setup & Objective
We'll assume that two Bayesian agents, Alice and Bob, each learn a probabilistic generative model, MA and MB respectively. Each model encodes a distribution P[X,Λi|Mi] over two "observable" random variables X1,X2 and some "latent" random variables Λi. Each model makes the same predictions about observables X, i.e.
∀x:P[X=x|MA]=P[X=x|MB] (Agreement on Observables)
However, the two generative models may use completely different latent variables ΛA and ΛB in order to model the generation of X (thus the different superscripts for Λ). Note that there might also be additional observables over which the agents disagree; i.e. X need not be all of the observables in the agents' full world models.
Crucially, we will assume that the agents can agree (or converge) on some way to break up X into individual observables X1,X2. (We typically picture X1,X2 as separated in time and/or space, but the math will not require that assumption.)
We require that the latents of each agent's model fully explain the interactions between the individual observables, as one would typically aim for when building a generative model. Mathematically, X1,X2⫫|Λi,Mi (read "X1,X2 are independent given Λi under model Mi"), or fully written out
∀i,x,λi:P[X=x|Λi=λi,Mi]=∏jP[Xj=xj|Λi=λi,Mi] (Mediation)
Given that Alice' and Bob's generative models satisfy these constraints (Agreement on Observables and Mediation), we'd like necessary and sufficient conditions under which Alice can guarantee that her latent is a function of Bob's latent. In other words, we'd like necessary and sufficient conditions under which Alice' latent ΛA is fully determined by Bob's latent ΛB, for any latent which Bob might use (subject to the constraints). Also, we'd like all of our conditions to be robust to approximation.
We will show that:
Notation
Throughout the paper, we will use the graphical notation of Bayes nets for equations. While our notation technically matches the standard usage in e.g. Pearl[5], we will rely on some subtleties which can be confusing. We will walk through the interpretation of the graph for the Mediation condition to illustrate.
The Mediation condition is shown graphically below.
The graph is interpreted as an equation stating that the distribution over the variables factors according to the graph - in this case, P[X,Λi]=P[Λi]∏jP[Xj|Λi]. Any distribution which factors this way "satisfies" the graph. Note that the graph does not assert that the factorization is minimal; for example, a distribution P[X1,X2,Λi] under which all Xi and Λi are independent - i.e. P[X1,X2,Λi]=P[Λi]∏jP[Xj] - satisfies all graphs over the variables X1,X2 and Λi, including the graph in the figure above.
Besides allowing for compact presentation of equations and proofs, the graphical notation also makes it easy to extend our results to the approximate case. When the graph is interpreted as an approximation, we write it with an approximation error ϵ underneath, as in the figure below.
In general, we say that a distribution P[Y1,...,Yn] "satisfies" a graph over variables Y1,...,Yn to within approximation error ϵ if and only if ϵ≥DKL(P[Y1,...,Yn]||∏jP[Yj|Ypa(j)]), where DKL is the KL divergence. We will usually avoid writing out these inequalities explicitly.
We'll also use a slightly unusual notation to indicate that one variable is a deterministic function of another: Y←X→Y. This diagram says that X mediates between Y and Y, which is only possible if Y is fully determined by X. Approximation to within ϵ works just like approximation for other diagrams, and turns out to reduce to ϵ≥H(Y|X):
ϵ≥DKL(P[X=x,Y=y,Y=y′]||P[X=x]P[Y=y|X=x]P[Y=y′|X=x])
=∑x,y,y′P[X=x,Y=y]I[y=y′](log(P[X=x,Y=y]I[y=y′])−log(P[X=x]P[Y=y|X=x]P[Y=y′|X=x]))
=∑x,yP[X=x,Y=y](log(P[X=x,Y=y])−log(P[X=x]P[Y=y|X=x]P[Y=y|X=x]))
=−∑x,yP[X=x,Y=y]log(P[Y=y|X=x])
=H(Y|X)
Foundational Concepts: Mediation, Redundancy & Naturality
Mediation and redundancy are the two main foundational conditions which we'll work with.
Readers are hopefully already familiar with mediation. We say a latent Λ "mediates between" observables X1,...,Xn if and only if X1,...,Xn are independent given Λ. Intuitively, any information shared across two or more Xj's must "go through" Λ. We call such a Λ a mediator. Canonical example: if X1,...,Xn are many rolls of a die of unknown bias Λ, then the bias is a mediator, since the rolls are all independent given the bias. See figure above for the graphical representation of mediation.
Redundancy is probably less familiar, especially the definition used here. We say a latent Λ′ is a "redund" over observables X1,...,Xn if and only if Λ′ is fully determined by each Xi individually, i.e. there exist functions fi such that Λ′=fi(Xi) for each i. In the approximate case, we weaken this condition to say that the entropy H(Λ′|Xi)≤ϵ for all i, for some approximation error ϵ.
Intuitively, all information about Λ′ must be redundantly represented across all Xi's. Canonical example: if X1,...,Xn are pixel values in small patches of a picture of a bike, and Λ′ is the color of the bike, then Λ′ is a redund insofar as we can back out the bike's color from any one of the little patches. In general, a latent Λ is approximately a redund over components of X if and only if ∀i:ϵ≥H(Λ|Xi) ("Redundancy") where ϵ=0 in the exact case. See below for the graphical representation of the redundancy condition.
We'll be particularly interested in cases where a single latent is both a mediator and a redund over X1,...,Xn. We call mediation and redundancy together the "naturality conditions", and we call a latent satisfying both mediation and redundancy a "natural latent". Canonical example: if X1,...,Xn are low level states of macroscopically separated chunks of a gas at thermal equilibrium, then the temperature is a natural latent over the chunks, since each chunk has the same temperature (thus redundancy) and the chunks' low-level states are independent given that temperature (thus mediation).
Justification of the name "natural latent" is the central purpose of this paper: roughly speaking, we wish to show that natural latents guarantee translatability, and that (absent further constraints) they are the only latents which guarantee translatability.
Core Theorems
We'll now present our core theorems. The next section will explain how these theorems apply to our motivating problem of translatability of latents across agents; readers more interested in applications and concepts than derivations should skip to the next section. We will state these theorems for generic latents Λ and Λ′, which we will tie back to our two agents Alice and Bob later.
Theorem: Mediator Determines Redund
Suppose that random variables X1,...,Xn, Λ, and Λ′ satisfy two conditions:
Then Λ′←Λ→Λ′.
In English: if one latent Λ mediates between the components of X, and another latent Λ′ is a redund over the components of X, then Λ′ is fully determined by Λ (or approximately fully determined, in the approximate case).
The graphical statement of the Mediator Determines Redund Theorem is shown below, including approximation errors. The proof is given in the Appendix.
The intuition behind the theorem is easiest to see when X has two components, X1 and X2. The mediation condition says that the only way information can "move between'' X1 and X2 is by "going through'' Λ. The redundancy conditions say that X1 and X2 must each alone be enough to determine Λ′, so intuitively, that information about Λ′ must have "gone through'' Λ - i.e. Λ must also be enough to determine Λ′. Thus, Λ′←Λ→Λ′; all the redund's information must flow through the mediator, so the mediator determines the redund.
Naturality ⟹ Minimality Among Mediators
We're now ready for the corollaries which we'll apply to translatability in the next section.
Suppose a latent Λ is natural over X1,...,Xn - i.e. it satisfies both the mediation and redundancy conditions. Well, Λ is a redund, so by the Mediator Determines Redund Theorem, we can take any other mediator Λ′′ and find that Λ←Λ′′→Λ. So: Λ is a mediator, and any other mediator is enough to determine Λ. So Λ is the "minimal" mediator: any other mediator must contain at least all the information which Λ contains. We sometimes informally call such a latent a "minimal latent".
Naturality ⟹ Maximality Among Redunds
There is also a simple dual to "Naturality ⟹ Minimality Among Mediators''. While the minimal latent conditions describe a smallest latent which mediates between X1,...,Xn, the dual conditions describe a largest latent which is redundant across X1,...,Xn. We sometimes informally call such a latent a "maximal latent".
Isomorphism of Natural Latents
If two latents Λ, Λ′ are both natural latents, then from the Mediator Determines Redund Theorem we trivially have both Λ′←Λ→Λ′ and Λ←Λ′→Λ. In English: the two latents are isomorphic.
In the approximate case, each latent has bounded entropy given the other; in that sense they are approximately isomorphic.
Application To Translatability
Motivating Question
Our main motivating question is: under what conditions on Alice' model MA and its latent(s) ΛA can Alice guarantee that ΛA is a function of ΛB (i.e. ΛA←ΛB→ΛA), for any model MB and latent(s) ΛB which Bob might have?
Recall that we already have some restrictions on Bob's model and latent(s): Agreement on Observables says P[X|MB]=P[X|MA], and Mediation says that X1,X2 are independent given ΛB under model MB.
Since Naturality ⟹ Minimality Among Mediators, the natural latent conditions seem like a good fit here. If Alice' latent ΛA satisfies the natural latent conditions, then Minimality Among Mediators says that for any latent Λ′′ satisfying mediation over X1,X2, ΛA←Λ′′→ΛA. And Bob's latent ΛB satisfies mediation, so we can take Λ′′=ΛB to get the result we want, trivially.
Guaranteed Translatability
If Alice' latent ΛA is natural, then it's a function of Bob's latent ΛB, i.e. ΛA←ΛB→ΛA. This is just the Naturality ⟹ Minimality Among Mediators theorem from earlier.
Now it's time for the other half of our main theorem: the naturality conditions are the only way for Alice to achieve this guarantee. In other words, we want to show: if Alice' latent ΛA satisfies Mediation, and for any latent ΛB Bob could choose (i.e. any other mediator) we have ΛA←ΛB→ΛA, then Alice' latent must be natural.
The key to the proof is then to notice that X1 trivially mediates between X1 and X2, and X2 also trivially mediates between X1 and X2. So, Bob could choose ΛB=X1, or ΛB=X2 (among many other options). In order to achieve her guarantee, Alice' latent ΛA must therefore satisfy ΛA←X1→ΛA and ΛA←X2→ΛA - i.e. redundancy over X1 and X2.
Alice' latent already had to satisfy the mediation condition by assumption, it must also satisfy the redundancy condition in order to achieve the desired guarantee, therefore it must be a natural latent. And if we weaken the conditions to allow approximation, then Alice' latent must be an approximate natural latent.
In English, the assumptions required for the theorem are:
Under those constraints, Alice can guarantee that her latent ΛA is a function of Bob's latent ΛB (i.e. ΛA←ΛB→ΛA) if and only if Alice' latent is a natural latent over X1,X2, meaning that it satisfies both the mediation condition (already assumed) and the redundancy condition ΛA←Xj→ΛA for all j.
Proof: the "if" part is just Naturality ⟹ Minimality Among Mediators; the "only if" part follows trivially from considering either ΛB=X1 or ΛB=X2 (both of which are always allowed choices of ΛB).
Natural Latents: Intuition & Examples
Having motivated the natural latent conditions as exactly those conditions which guarantee translatability, we move on to building some intuition for what natural latents look like and when they exist.
When Do Natural Latents Exist? Some Intuition From The Exact Case
For a given distribution P[X1,...,Xn], a natural latent over X does not always exist, whether exact or approximate to within some error ϵ. In practice, the cases where interesting natural latents do exist usually involve approximate natural latents (as opposed to exact), and we'll see some examples in the next section. But first, we'll look at the exact case, in order to build some intuition.
Let's suppose that there are just two observables X1,X2. If Λ is natural over those two observables, then the redundancy conditions say Λ=f1(X1)=f2(X2) for some functions f1,f2. That means
f1(X1)=f2(X2) with probability 1
This is a deterministic constraint between X1 and X2.
Next, the mediation condition. The mediation condition says that X1 and X2 are independent given Λ - i.e. they're independent given the value of the deterministic constraint. So: assuming existence of a natural latent Λ, X1 and X2 must be independent given the value of a deterministic constraint.
On the other hand, if X1 and X2 are independent given the value of a deterministic constraint, then the value of the constraint clearly satisfies the natural latent conditions.
That gives us an intuitive characterization of the existence conditions for exact natural latents: an exact natural latent between two (or more) variables exists if-and-only-if the variables are independent given the value of a deterministic constraint across those variables.
Worked Quantitative Example of the Mediator Determines Redund Theorem
Consider Carol who is about to flip a biased coin she models as having some bias Λ. Carol flips the coin 1000 times, computes the median of the flips, then flips the coin another 1000 times and computes the median of that batch. For simplicity, we assume a uniform prior on Λ over the interval [0,1].
Intuitively, if the bias Λ is unlikely to be very close to12, Carol will find the same median both times with high probability. Let X1 and X2 denote Carol's first and second batches of 1000 flips, respectively. Note that the flips are independent given Λ, under her model, satisfying the mediation condition of the Mediator Determines Redund Theorem, exactly. Let Λ′ be the median computed from either of the batches. Since the same median can be computed with high probability from eitherX1 or X2, the redundancy condition is approximately satisfied.
The Mediator Determines Redund Theorem, then tells us that the bias approximately mediates between the median (computed from either batch) and the coinflips X. To quantify the approximation, we first quantify the approximation on the redundancy condition (the other two conditions hold exactly, so their ϵ's are 0). Taking Λ′ to be Carol's calculation of the median from the first batch, X1, Carol's median can be exactly determined from those flips (i.e., Λ′←X1→Λ′), but Carol's median of the first batch can be determined from the second batch of flips (i.e., Λ′←X2→Λ′) only approximately. The approximation error is E[H(Λ′(X1)|X2)].
This is a Dirichlet-multinomial distribution, so it is cleaner to rewrite in terms of N1:=∑X1, N2:=∑X2, and n:=1000. Since Λ′ is a function of N1, the approximation error becomes H(Λ′(N1)|N2).
Writing out the distribution and simplifying the gamma functions, we obtain:
P[N2]=1n+1 (i.e., uniform over 0, ..., n)
P[N1|N2]=Γ(n+2)Γ(N2+1)Γ(n−N2+1)Γ(n+1)Γ(N1+1)Γ(n−N1+1)Γ(N1+N2+1)Γ(2n−N1−N2+1)Γ(2n+2)
P[Λ′(N1)=0|N2]=∑n1<500P[N1|N2]
P[Λ′(N1)=1|N2]=∑n1>500P[N1|N2]
There are only 10012 values of (N1,N2), so these expressions can be combined and evaluated using a Python script (see Appendix for code). The script yields H=0.058 bits. As a sanity check, the main contribution to the entropy should be when Λ is near 0.5, in which case the median should have roughly 1 bit of entropy. With n data points, the posterior uncertainty should be of order 1√n, so the estimate of Λ should be precise to roughly 130≈.03 in either direction. Since Λ is initially uniform on [0,1], a distance of 0.03 in either direction around 0.5 covers about 0.06 in prior probability, and the entropy should be roughly 0.06 bits, which is consistent with the computed value.
Returning to the Mediator Determines Redund Theorem, we have ϵmed=0 and ϵred≈0.058 bits. Thus, the theorem states that Carol's median is approximately determined by the coin's bias, Λ, to within ϵmed+2ϵred≈0.12 bits of entropy.
Exercise for the Reader: By separately tracking the ϵ's on the two redundancy conditions through the proof, show that, for this example, the coin's true bias approximately mediates between the coinflips and Carol's median to within ϵred, i.e., roughly 0.058 bits.
Intuitive Examples of Natural Latents
This section will contain no formalism, but will instead walk through a few examples in which one would intuitively expect to find a nontrivial natural latent, in order to help build some intuition for the reader. The When Do Natural Latents Exist? section provides the foundations for the intuitions of this section.
Ideal Gas
Consider an equilibrium ideal gas in a fixed container, through a Bayesian lens. Prior to observing the gas, we might have some uncertainty over temperature. But we can obtain a very precise estimate of the temperature by measuring any one mesoscopic chunk of the gas. That's an approximate deterministic constraint between the low-level states of all the mesoscopic chunks of the gas: with probability close to 1, they approximately all yield approximately the same temperature estimate.
Due to chaos, we also expect that the low-level state of mesoscopic chunks which are not too close together spatially are approximately independent given the temperature.
So, we have a system in which the low-level states of lots of different mesoscopic chunks are approximately independent given the value of an approximate deterministic constraint (temperature) between them. Intuitively, those are the conditions under which we expect to find a nontrivial natural latent. In this case, we expect the natural latent to be approximately (isomorphic to) temperature.
Biased Die
Consider 1000 rolls of a die of unknown bias. Any 999 of the rolls will yield approximately the same estimate of the bias. That's (approximately) the redundancy condition for the bias.
We also expect that the 1000 rolls are independent given the bias. That's the mediation condition. So, we expect the bias is an approximate natural latent over the rolls.
However, the approximation error bound in this case is quite poor, since our proven error bound scales with the number n of observables. We can easily do better by viewing the first 500 and second 500 rolls as two observables. We expect that the first 500 rolls and the second 500 rolls will yield approximately the same estimate of the bias, and that the first 500 and second 500 rolls are independent given the bias, so the bias is a natural latent between the first and second 500 rolls of the die. This view of the problem will likely yield much better error bounds. More generally, chunking together many observables this way typically provides much better error bounds than applying the theorems directly to many observables.
Timescale Separation In A Markov Chain
In a Markov Chain, timescale separation occurs when there is some timescale T such that, if the chain is run for T steps, then the state can be split into a component which is almost-certainly conserved over the T steps and a component which is approximately ergodic over the T steps. In that case, we expect both the initial state and Tth state to almost-certainly yield the same estimate of the conserved component, and we expect that the initial state and Tth state are approximately independent given the conserved component, so the conserved component should be an approximate natural latent between the initial and Tth state.
Discussion & Conclusion
We began by asking when one agent's latent can be guaranteed to be expressible in terms of another agent's latent(s), given that the two agree on predictions about two observables. We've shown that:
...for a specific broad class of possibilities for the other agent's latent(s). In particular, the other agent can use any latent(s) which fully explain the interactions between the two observables. So long as the other agent's latent(s) are in that class, the first agent can guarantee that their latent can be expressed in terms of the second's exactly when the natural latent conditions are satisfied.
These results provide a potentially powerful tool for many of the questions posed at the beginning.
When is robust translation possible at all, between agents with potentially different internal concepts, like e.g. humans and AI, or humans from different cultures? Insofar as the agents make the same predictions about two parts of the world, and both their latent concepts induce independence between those parts of the world (including approximately), either agent can ensure robust translatability into the other agent's ontology by using a natural latent. In particular, if the agents are trying to communicate, they can look for parts of the world over which natural latents exist, and use words to denote those natural latents; the equivalence of natural latents will ensure translatability in principle, though the agents still need to do the hard work of figuring out which words refer to natural latents over which parts of the world.
Under what conditions are scientific concepts guaranteed to carry over to the ontologies of new theories, like how e.g. general relativity has to reduce to Newtonian gravity in the appropriate limit? Insofar as the old theory correctly predicted two parts of the world, and the new theory introduces latents to explain all the interactions between those parts of the world, the old theorist can guarantee forward-compatibility by working with natural latents over the relevant parts of the world. This allows scientists a potential way to check that their work is likely to carry forward into as-yet-unknown future paradigms.
When and why might a wide variety of minds in the same environment converge to use (approximately) the same concept internally? While this question wasn't the main focus of this paper, both the minimality and maximality conditions suggest that natural latents (when they exist) will often be convergently used by a variety of optimized systems. For minimality: the natural latent is the minimal variable which mediates between observables, so we should intuitively expect that systems which need to predict some observables from others and are bandwidth-limited somewhere in that process will often tend to represent natural latents as intermediates. For maximality: the natural latent is the maximal variable which is redundantly represented, so we should intuitively expect that systems which need to reason in ways robust to individual inputs will often tend to track natural latents.
The natural latent conditions are a first step toward all these threads. Most importantly, they offer any mathematical foothold at all on such conceptually-fraught problems. We hope that foothold will both provide a foundation for others to build upon in tackling such challenges both theoretically and empirically, and inspire others to find their own footholds, having seen that it can be done at all.
Acknowledgements
We thank the Long Term Future Fund and the Survival and Flourishing Fund for funding this work.
Appendices
Graphical Notation and Some Rules for Graphical Proofs
In this paper, we use the diagrammatic notation of Bayes networks (Bayes nets) to concisely state properties of probability distributions. Unlike the typical use of Bayes nets, where the diagrams are used to define a distribution, we assume that the joint distribution is given and use the diagrams to express properties of the distribution.
Specifically, we say that a distribution P[Y] "satisfies" a Bayes net diagram if and only if the distribution factorizes according to the diagram's structure. In the case of approximation, we say that P[Y] "approximately satisfies" the diagram, up to some ϵ≥0, if and only if the Kullback-Leibler divergence (DKL) between the true distribution and the distribution implied by the diagram is less than or equal to ϵ.
Frankenstein Rule
Statement
Let P[X1,…,Xn] be a probability distribution that satisfies two different Bayes networks, represented by directed acyclic graphs G1 and G2. If there exists an ordering of the variables X1,…,Xn that respects the topological order of both G1 and G2 simultaneously, then P[X1,…,Xn] also satisfies any "Frankenstein" Bayesian network constructed by taking the incoming edges of each variable Xi from either G1 or G2.
More generally, if P[X1,…,Xn] satisfies m different Bayes networks G1,…,Gm, and there exists an ordering of the variables that respects the topological order of all m networks simultaneously, then P[X1,…,Xn] satisfies any "Frankenstein" Bayes network constructed by taking the incoming edges of each variable Xi from any of the m original networks.
We'll prove the approximate version, then the exact version follows trivially.
Proof
Without loss of generality, assume the order of variables respected by all original diagrams is X1,…,Xn. Let P[X]=∏iP[Xi|Xpaj(i)] be the factorization expressed by diagram j, and let σ(i) be the diagram from which the parents of Xi are taken to form the Frankenstein diagram. (The factorization expressed by the Frankenstein diagram is then P[X]=∏iP[Xi|Xpaσ(i)(i)].)
The proof starts by applying the chain rule to the DKL of the Frankenstein diagram:
DKL(P[X]||∏iP[Xi|Xpaσ(i)(i)])=DKL(∏iP[Xi|X<i]||∏iP[Xi|Xpaσ(i)(i)])
= ∑iE[DKL(P[Xi|X<i]||P[Xi|Xpaσ(i)(i)])]
Then, we add a few more expected KL-divergences (i.e., add some non-negative numbers) to get:
≤∑i∑jE[DKL(P[Xi|X<i]||P[Xi|Xpaj(i)])]
= ∑jDKL(P[X]||∏iP[Xi|Xpaj(i)])
≤∑jϵj
Thus, we have
DKL(P[X]||∏iP[Xi|Xpaσ(i)(i)])≤∑jDKL(P[X]||∏iP[Xi|Xpaj(i)])
≤∑jϵj
Factorization Transfer
Statement
Let P[X1,…,Xn] and Q[X1,…,Xn] be two probability distributions over the same set of variables. If Q satisfies a given factorization (represented by a diagram) and Q approximates P with an error of at most ϵ, i.e.,
ϵ≥DKL(P||Q)
then P also approximately satisfies the same factorization, with an error of at most ϵ:
ϵ≥DKL(P[X1,…,Xn]||∏iP[Xi|Xpa(i)])
where Xpa(i) denotes the parents of Xi in the diagram representing the factorization.
Proof
As with the Frankenstein rule, we start by splitting our DKL into a term for each variable:
DKL(P[X]||Q[X])=∑iE[DKL(P[Xi|X<i]||Q[Xi|Xpa(i)])]
Next, we subtract some more DKL's (i.e., subtract some non-negative numbers) to get:
≥∑i(E[DKL(P[Xi|X<i]||Q[Xi|Xpa(i)])]−E[DKL(P[Xi|Xpa(i)]||Q[Xi|Xpa(i)])])
=∑iE[DKL(P[Xi|X<i]||P[Xi|Xpa(i)])]
=DKL(P[X]||∏iP[Xi|Xpa(i)])
Thus, we have
DKL(P[X]||Q[X])≥DKL(P[X]||∏iP[Xi|Xpa(i)])
Bookkeeping Rule
Statement
If all distributions which exactly factor over Bayes net G1 also exactly factor over Bayes net G2, then:
DKL(P[X]||∏iQ[Xi∣XpaG2(i)])≥DKL(P[X]||∏iP[Xi∣XpaG2(i)])
Proof
Let Q[X]:=∏iP[Xi∣XpaG1(i)]. By definition, Q factors over G1. Since all distributions which factor over G1 also factor over G2, it follows that Q also factors over G2.
Now, we have:
Q[X]=∏iQ(Xi∣XpaG2(i))
Thus:
DKL(P[X]||∏iP(Xi∣XpaG1(i)))=DKL(P[X]||∏iQ(Xi∣XpaG2(i)))
By the Factorization Transfer Theorem, we have:
DKL(P[X]||∏iQ(Xi∣XpaG2(i)))≥DKL(P[X]||∏iP(Xi∣XpaG2(i)))
which completes the proof.
The Dangly Bit Lemma
Statement
If Y←X→Y holds to within ϵ bits, and any other diagram D involving X holds to within ϵ′ bits, then we can create a new diagram D′ which is identical to D but has another copy of Y (the "dangly bit'') as a child of X. The new diagram D′ will hold to within ϵ+ϵ′ bits.
Proof
Let Q[X,Z] be the distribution over X and other variables Z specified by D (with Z possibly containing copies of Y). Then D′ specifies the distribution Q[X,Z]P[Y∣X], so the approximation error for D′ is:
DKL(P[X,Y,Z]∥Q[X,Z]P[Y∣X])
=DKL(P[X,Z]∥Q[X,Z])+EX,Z[DKL(P[Y∣X,Z]∥P[Y∣X])]
=DKL(P[X,Z]∥Q[X,Z])+I(Y;Z∣X)
≤DKL(P[X,Z]∥Q[X,Z])+H(Y∣X)
≤ϵ′+ϵ.
Graphical Proofs
Python Script for Computing DKL in Worked Example
W. V. O. Quine, On empirically equivalent systems of the world, Erkenntnis 9, 313 (1975).
H. Cunningham, A. Ewart, L. Riggs, R. Huben, and L. Sharkey, Sparse autoencoders find highly interpretable features in
language models, (2023), arXiv:2309.08600 [cs.LG].
Marvik, Model merging: Combining different fine-tuned LLMs, Blog post (2024), retrieved from https://marvik.com/
model-merging.
M. Huh, B. Cheung, T. Wang, and P. Isola, The platonic representation hypothesis, (2024), arXiv:2405.07987 [cs.LG].
J. Pearl, Causality: Models, Reasoning and Inference, 2nd ed. (Cambridge University Press, USA, 2009).