James Camacho's Shortform

22nd Jul 2023

1 min read

2

This is a special post for quick takes by James Camacho. Only they can create top-level comments. Comments here also appear on the Quick Takes page and All Posts page.

James Camacho's Shortform

16 comments, sorted by

top scoring

Click to highlight new comments since: Today at 11:29 AM

[-]James Camacho1mo15-13

There is a lot of confusion around the determinant, and that's because it isn't taught properly. To begin talking about volume, you first need to really understand what space is. The key is that points in space like aren't the thing you actually care about—it's the values you assign to those points. Suppose you have some generic function, fiber, you-name-it, that takes in points and spits out something else. The function may vary continuously along some dimensions, or even vary among multiple dimensions at the same time. To keep track of this, we can attach tensors to every point:

d x_{1} \otimes d x_{2} \otimes \dots \otimes d x_{n}

Or maybe a sum of tensors:

d x_{1} \otimes d x_{2} \otimes \dots \otimes d x_{n} + d x_{2} \otimes d x_{1} + \dots

The order in that second tensor is a little strange. Why didn't I just write it like

d x_{1} \otimes d x_{2} ?

It's because sometimes the order matters! However, what we can do is break up the tensors into a sum of symmetric pieces. For example,

d x_{2} \otimes d x_{1} = \frac{1}{2} [d x_{1} \otimes d x_{2} + d x_{2} \otimes d x_{1}]      symmetric - \frac{1}{2} [d x_{1} \otimes d x_{2} - d x_{2} \otimes d x_{1}]      antisymmetric .

To find all the symmetric pieces in higher dimensions, you take the symmetric group $S_{n}$ and compute its irreducible representations (re: the Schur-Weyl duality). Irreducible representations are orthogonal, so each of these symmetric pieces don't really interact with each other. If you only care about one of the pieces (say the antisymmetric one) you only need to keep track of the coefficient in front of it. So,

d x_{2} \otimes d x_{1} = - \frac{1}{2} d x_{1} \land d x_{2}      antisymmetric + other pieces .

We could also write the antisymmetric piece as

+ \frac{1}{2} d x_{2} \land d x_{1}      reverse order!

and this is where the determinant comes from! It turns out that our physical world seems to only come from the antisymmetric piece, so when we talk about volumes, we're talking about summing stuff like

d x_{1} \land d x_{2} \land \dots \land d x_{n} .

If we have vectors

\begin{matrix} a_{1} & = a_{11} d x_{1} + a_{12} d x_{2} + \dots + a_{1 n} d x_{n} a_{2} & = a_{21} d x_{1} + a_{22} d x_{2} + \dots + a_{2 n} d x_{n} ⋮ a_{n} & = a_{n 1} d x_{1} + a_{n 2} d x_{2} + \dots + a_{n n} d x_{n} \end{matrix}

then the volume between them is

a_{1} \land a_{2} \land \dots \land a_{n} .

Note that

d x_{i} \land d x_{i} = - d x_{i} \land d x_{i} ⟹ d x_{i} \land d x_{i} = 0

so we're only looking for terms where no $d x_{i}$ overlap, or equivalently terms with every $d x_{i}$ . These are

\sum σ \in S_{n} (a_{1 σ_{1}} d x_{σ_{1}}) \land (a_{2 σ_{2}} d x_{σ_{2}}) \land \dots \land (a_{n σ_{n}} d x_{σ_{n}})

or rearranging so they show up in the same order,

\sum σ \in S_{n} (- 1)^{s g n (σ)} n \prod i = 1 a_{i σ_{i}} n ⋀ i = 1 d x_{i} .

[-]speck14471mo61

Strongly disagree that this is the right way to think about the determinant. It's pretty easy to start with basic assumptions about the signed volume form (flat things have no volume, things that are twice as big are twice as big) and get everything. Or we might care about exterior algebras, at which point the determinant pops out naturally. Lie theory gives us a good reason to care about the exterior algebra - we want to be able to integrate on manifolds, so we need some volume form, and if we differentiate tensor products of differentiable things by the Leibniz rule, then invariance becomes exactly antisymmetry (in other words, we want our volume form to be a Haar measure for ). Or if we really want to invoke representation theory, the determinant is the tensor generator of linear algebraic characters of $GL (V)$ , and the functoriality that implies is maybe the most important fact about the determinant. Schur-Weyl duality is extremely pretty but I usually think of it as saying something about $S_{n}$ more than it says something about $GL (V)$ . (Fun to think about: we often write the determinant, as you did, as a sum over elements of $S_{n}$ of products of matrix entries with special indexing, times some function from $S_{n}$ to $C$ . What do properties of the determinant (say linearity, alternativity, functoriality) imply about that function? Does this lead to a more mechanistic understanding of Schur-Weyl duality?)

[-]James Camacho1mo10

The terms you're invoking already assume you're living in antisymmetric space.

Signed volume / exterior algebra (literally the space).
Derivatives and integrals come from the boundary operator , and the derivative/integral you're talking about is $ρ (σ) = (- 1)^{s g n (σ)}$ . That is why some people write their integrals as $\int f (x) \land d x$ .

It is a nice propery that $det : G L (V) \to F$ happens to be the only homomorphism (because $s g n$ is one-dimensional), but why do you want this property? My counterintuition is, what if we have a fractal space where distance shouldn't be $ℓ_{2}$ and volume is a little strange? We shouldn't expect the volume change from a series of transformations to be the same as a series of volume changes.

[-]speck14471mo40

The terms you're invoking already assume you're living in antisymmetric space.

I think this is the other way around. We could decide to only care about the alternating tensors, sure, but your explanation for why we care about this component of the tensor algebra in particular is just "it turns out" that the physical world works like this. I'm trying to explain that we could have known this in advance, it's natural to expect the alternating component to be particularly nice.

I think my answers to your other two questions are basically the same so I'll write a longer paragraph here:

We can think of derivatives and integrals as coming from a boundary operator, sure, but this isn't "the" boundary operator, because it's only defined up to simplicial structure and we might choose many simplicial structures! In practice we don't depend on a simplicial structure at all. We care a lot about doing calculus on (smooth) manifolds - we want to integrate over membranes or regions of spacetime, etc. With manifolds we get smooth coordinate charts, local coordinates with some compatibility conditions to make calculus work, and this makes everything nice! To integrate something on a manifold, you integrate it on the coordinate charts via an isomorphism to (we could work over complex manifolds instead, everything is fine), you lift this back to the manifold, everything works out because of the compatibility. Except that we made a lot of choices in this procedure: we chose a particular smooth atlas, we chose particular coordinates on the charts. Our experience from $R^{n}$ tells us that these choices shouldn't matter too much, and we can formalize how little they should matter.

There's a particularly nice smooth atlas, where every point gets local coordinates that are essentially the projection from its tangent space. Now what sorts of changes of coordinates can we do? The integral maps nice functions on our manifold to our base field (really we want to think of this as a map of covectors). That should give us a linear map on tangent spaces, and this map should respect change of basis - that is, change-of-basis should look like some map ${GL}_{R} (n) \to R$ , and functoriality comes from the universal property of the tangent space. We're not just looking at transformations, locally we're looking at change of basis, and we expect the effect of changing from basis $A$ to $B$ to $C$ to just be the same as changing from $A$ to $C$ . All we're asking for is a special amount of linearity, and linearity is exactly what we expect when working with manifolds.

All this to say, we want a homomorphism because we want to do calculus on smooth manifolds, because physics gives us lots of smooth manifolds and asks us to do calculus on them. This is "why" the alternating component is the component we actually care about in the tensor algebra, which is a step you didn't motivate in your original explanation, and motivating this step makes the rest of the explanation redundant.

(Now you might reasonable ask, where does the fractal story fit into this? What about non-Hausdorff measures? These integrals aren't functorial, sure. They're also not absolutely continuous, they don't respect this linear structure or the manifold structure. One reason measure theory is useful is because it can simultaneously formalize these two different notions of size, but that doesn't mean these notions are comparable - measure theory should be surprising to you, because we shouldn't expect a single framework to handle these notions simultaneously. Swapping from one measure to another implies a huge change in priorities, and these aren't the priorities we have when trying to define the sorts of integrals we encounter in physics.)

(You might also ask, why are we expecting the action to be local? Why don't we expect $GL (n)$ to do different things in different parts of our manifold? And I think the answer is that we want these transformations to leave the transitions between charts intact and gauge theory formalizes the meaning of "intact" here, but I don't actually know gauge theory well enough to say more.)

(Third aside, it's true that derivatives and integrals come from the double differential being 0, but we usually don't use the simplicial boundary operator you describe, we use the de Rham differential. The fact that these give us the same cohomology theory is really extremely non-obvious and I don't know a proof that doesn't go through exterior powers. You can try to define calculus with reference to simplicial structures like this, but a priori it might not be the calculus you expect to get with the normal exterior power structure, it might not be the same calculus you would get with a cubical structure, etc.)

(Fourth aside, I promise this is actually the last one, the determinant isn't the only homomorphism. It tensor generates the algebraic homomorphisms, meaning ${det}^{- 1}, {det}^{2}, {det}^{3}, \dots$ are also homomorphisms, and there are often non-algebraic field automorphisms, so properly we should be looking at $φ \circ {det}^{k}$ for any integer $k$ and any field automorphism $φ$ . But in practice we only care about algebraic representations and the linear one is special so we care about the determinant in particular.)

[-]jacob_drori1mo3-1

To begin talking about volume, you first need to really understand what space is.

No, stop it, this is a terrible approach to math education. "Ok kids, today we're learning about the area of a circle. First, recall the definition of a manifold." No!!

[-]Algon1mo20

I always liked this way of looking at the determinant.

[-]James Camacho1mo50

The Utility Engineering paper found hyperbolic discounting.

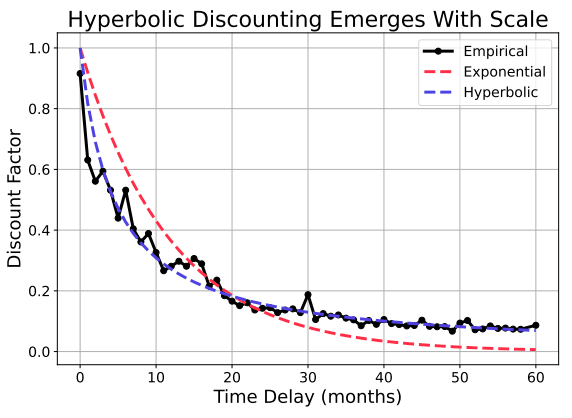
Eyeballing it, this is about

This was pretty surprising to me, because I've always assumed discount rates should be timeless. Why should it matter if I can trade $1 today for $2 tomorrow, or $1 a week from now for $2 a week and a day from now? Because the money-making mechanism survived. The longer it survives, the more evidence we have it will continue to survive. Loosely, if the hazard rate $H$ is proportional to the survival (and thus discount) probability $U$ , we get

\begin{matrix} U & = k H, \frac{d}{d t} U & = - U H ⟹ U (t) & = \frac{1}{1 + \frac{t}{k}} . \end{matrix}

More rigorously, suppose there is some distribution of hazards in the environment. Maybe the opportunity could be snatched by someone else, maybe you could die and lose your chance at the opportunity, or maybe the Earth could get hit by a meteor. If we want to maximize the entropy of our prior for the hazard distribution, or we want it to be memoryless—so taking into account some hazards gives the same probability distribution for the rest of the hazards—the hazard rate should follow an exponential distribution

Pr [H (0) = h] \propto e^{- k h} .

By Bayes' rule, the posterior after some time $t$ is

Pr [H (t) = h] \propto e^{- (k + t) h}

and the expected hazard rate is

E [H (t)] = \frac{1}{k + t} .

By linearity of expectation, we recover the discount factor

U (t) = \frac{1}{1 + \frac{t}{k}} .

I'm now a little partial to hyperbolic discounting, and surely the market takes this into account for company valuations or national bonds, right? But that is for another day (or hopefully a more knowledgeable commenter) to find out.

[-]James Camacho1y3-1

Religious freedoms are a subsidy to keep the temperature low. There's the myth that societies will slowly but surely get better, kind of like a gradient descent. If we increase the temperature too high, an entropic force would push us out of a narrow valley, so society could become much worse (e.g. nobody wants the Spanish Inquisition). It's entirely possible that the stable equilibrium we're being attracted to will still have religion.

[-]robo1y30

I want to love this metaphor but don't get it at all. Religious freedom isn't a narrow valley; it's an enormous Shelling hyperplane. 85% of people are religious, but no majority is Christian or Hindu or Kuvah'magh or Kraẞël or Ŧ̈ř̈ȧ̈ӎ͛ṽ̥ŧ̊ħ or Sisters of the Screaming Nightshroud of Ɀ̈ӊ͢Ṩ͎̈Ⱦ̸Ḥ̛͑.. These religions don't agree on many things, but they all pull for freedom of religion over the crazy *#%! the other religions want.

[-]James Camacho2y2-1

Graph Utilitarianism:

People care about others, so their utility function naturally takes into account utilities of those around them. They may weight others' utilities by familiarity, geographical distance, DNA distance, trust, etc. If every weight is nonnegative, there is a unique global utility function (Perron-Frobenius).

Some issues it solves:

Pascal's mugging.
The argument "utilitarianism doesn't work because you should care more about those around you".

Big issue:

In a war, people assign negative weights towards their enemies, leading to multiple possible utility functions (which say the best thing to do is exterminate the enemy).

[-]Dagon2y20

This is a very imprecise use of “utility”. Caring about others does not generally take their utility into account.

It takes one’s model of the utility that one thinks the others should have into account.

And, as you note, even this isn’t consistent across people or time.

[-]James Camacho1y10

Risk is a great study into why selfish egoism fails.

I took an ethics class at university, and mostly came to the opinion that morality was utilitarianism with an added deontological rule to not impose negative externalities on others. I.e. "Help others, but if you don't, at least don't hurt them." Both of these are tricky, because anytime you try to "sum over everyone" or have any sort of "universal rule" logic breaks down (due to Descartes' evil demon and Russell's vicious circle). Really, selfish egoism seemed to make more logical sense, but it doesn't have a pro-social bias, so it makes less sense to adopt when considering how to interact with or create a society.

The great thing about societies is we're almost always playing positive-sum games. After all, those that aren't don't last very long. Even if my ethics wasn't well-defined, the actions proscribed will usually be pretty good ones, so it's usually not useful to try to refine that definition. Plus, societies come with cultures that have evolved for thousands of years to bias people to act decently, often without needing to think how this relates to "ethics". For example, many religious rules seem mildly ridiculous nowadays, but thousands of years ago they didn't need to know why cooking a goatchild in its mother's milk was wrong, just to not do it.

Well, all of this breaks down when you're playing Risk. The scarcity of resources is very apparent to all the players, which limits the possibility for positive-sum games. Sure, you can help each other manoeuvre your stacks at the beginning of the game, or one-two slam the third and fourth players, but every time you cooperate with someone else, you're defecting against everyone else. This is probably why everyone hates turtles so much: they only cooperate with themselves, which means they're defecting against every other player.

I used to be more forgiving of mistakes or idiocracy. After all, everyone makes mistakes, and you can't expect people to take the correct actions if they don't know what they are! Shouldn't the intentions matter more? Now, I disagree. If you can't work with me, for whatever reason, I have to take you down.

One game in particular comes to mind. I had the North American position and signalled two or three times to the European and Africa+SA players to help me slam the Australian player. The Africa player had to go first, due to turn order and having 30 more troops; instead, they just sat and passed. The Australian player was obviously displeased about my intentions, and positioned their troops to take me out, so I broke SA and repositioned my troops there. What followed was a huge reshuffle (that the Africa player made take wayy longer due to their noobery), and eventually the European player died off. Then, again, I signal to the former Africa player to kill the Australian player, and again, they just sit and take a card. I couldn't work with them, because they were being stupid and selfish. 'And', because that kind of selfishness is rather stupid. Since I couldn't go first + second with them, I was forced to slam into them to guarantee second place. If they were smart about being selfish, they would have cooperated with me.

As that last sentence alludes to, selfish egoism seems to make a lot of sense for a moral understanding of Risk. Something I've noticed is almost all the Grandmasters that comment on the subreddit, or record on YouTube seem to have similar ideas:

"Alliances" are for coordination, not allegiances.
Why wouldn't you kill someone on twenty troops for five cards?
It's fine to manipulate your opponents into killing each other, especially if they don't find out. For example, stacking next to a bot to get your ally's troops killed, or cardblocking the SA position when in Europe and allied with NA and Africa.

This makes the stupidity issue almost more of a crime than intentionally harming someone. If someone plays well and punishes my greed, I can respect that. They want winning chances, so if I give them winning chances, they'll work with me. But if I'm stupid, I might suicide my troops into them, ruining both of our games. Or, if someone gets their Asia position knocked out by Europe, I can understand them going through my NA/Africa bonus to get a new stack out. But, they're ruining both of our games if they just sit on Central America or North Africa. And, since I'm smart enough, I would break the Europe bonus in retaliation. If everyone were smart and knew everyone else was smart, the Europe player wouldn't knock out the SA player's Asia stack. People wouldn't greed for both Americas while I'm sitting in Africa. So on and so forth. Really, most of the "moral wrongs" we feel when playing Risk only occur because one of us isn't smart enough!

My view on ethics has shifted; maybe smart selfish egoism really is a decent ethics to live by. However, also evidenced by Risk, most people aren't smart enough to work with, and most that are took awhile to get there. I think utilitaranism/deontology works better because people don't need to think as hard to take good actions. Even if they aren't necessarily the best, they're far better than most people would come up with!

[-]James Camacho10mo-1-2

Why are conservatives for punitive correction while progressives do not think it works? I think this can be explained by the difference between stable equilibria and saddle points.

If you have a system where people make random "mistakes" an amount of the time, the stable points are known as trembling-hand equilibria. Or, similarly, if they transition to different policies some H of the time, you get some thermodynamic distribution. In both models, your system is exponentially more likely to end up in states it is hard to transition out of (Ellison's lemma & the Boltzmann distribution respectively). Societies will usually spend a lot of time at a stable equilibrium, and then rapidly transition to a new one when the temperature increaes, in a way akin to simulated annealing. Note that we're currently in one of those transition periods, so if you want to shape the next couple decades of policy, now is the time to get into politics.

In stable equilibria, punishment works. It essentially decreases $ϵ$ so it's less likely for too many people to make a mistake at the same time, conserving the equilibrium. But progressives are climbing a narrow mountain pass, not sitting at the top of a local maximum. It's much easier for disaffected members to shove society off the pass, so a policy of punishing defectors is not stable—the defectors can just defect more and win. This is why punishment doesn't work; the only way forward is if everyone goes along with the plan.

[-]James Camacho1y-3-2

Is there a difference between utilitarianism and selfish egoism?

For utilitarianism, you need to choose a utility function. This is entirely based on your preferences: what you value, and who you value get weighed and summed to create your utility function. I don't see how this differs from selfish egoism: you decide what and who you value, and take actions that maximize these values.

Each doctrine comes with a little brainwashing. Utilitarianism is usually introduced as summing "equally" between people, but we all know some arrangements of atoms are more equal than others. However, introducing it this way naturally leads people to look for cooperation and value others more, both of which increase their chance of surviving.

Ayn Rand was rather reactionary against religion and its associated sacrificial behavior, so selfish egoism is often introduced as a reaction:

When you die, everything is over for you. Therefore, your survival is paramount.
You get nothing out of sacrificing your values. Therefore, you should only do things that benefit you.

Kant claimed people are good only by their strength of will. Wanting to help someone is a selfish action, and therefore not good. Rand takes the more individually rational approach: wanting to help someone makes you good, while helping someone against your interests is self-destructive. To be fair to Kant, when most agents are highly irrational your society will do better with universal laws than moral anarchy. This is also probably why selfish egoism gets a bad rapport: even if you are a selfish egoist, you want to influence your society to be more Kantian. Or, at the very least, like those utilitarians. They at least claim to value others.

However, I think rational utilitarians really are the same as rational selfish egoists. A rational selfish egoist would choose to look for cooperation. When they have fundamental disagreements with cooperative others, they would modify their values to care more about their counterpart so they both win. In the utilitarian bias, it's more difficult to realize when to change your utility function, while it's a little easier with selfish egoism. After all, the most important thing is survival, not utility.

I think both philosophies are slightly wrong. You shouldn't care about survival per se, but expected discounted future entropy (i.e. how well you proliferate). This will obviously drop to zero if you die, but having a fulfilling fifty years of experiences is probably more important than seventy years in a 2x2 box. Utility is merely a weight on your chances of survival, and thus future entropy. ClosedAI is close with their soft actor-critic, though they say it's entropy-regularized reinforcement learning. In reality, all reinforcement learning is maximizing energy-regularized entropy.

[-]Viliam1y00

For utilitarianism, you need to choose a utility function. This is entirely based on your preferences: what you value, and who you value get weighed and summed to create your utility function. I don't see how this differs from selfish egoism: you decide what and who you value, and take actions that maximize these values.

I see a difference in the word "summed". In practice this would probably mean things like cooperating in the Prisoner's Dilemma (maximizing the sum of utility, rather than the utility of an individual player).

[-]James Camacho1y1-1

Utilitarianism is usually introduced as summing "equally" between people, but we all know some arrangements of atoms are more equal than others.

How do you choose to sum the utility when playing a Prisoner's Dilemma against a rock?

[+][comment deleted]1mo10

Moderation Log

LESSWRONG
LW

LESSWRONG
LW

James Camacho's Shortform

2