ABSTRACT: We introduce a straightforward yet effective method to break down transformer outputs into individual components. By treating the model’s non-linear activations as constants, we can decompose the output in a linear fashion, expressing it as a sum of contributions. These contributions can be easily calculated using linear projections. We call this approach “logit prisms” and apply it to analyze the residual streams, attention layers, and MLP layers within transformer models. Through two illustrative examples, we demonstrate how these prisms provide valuable insights into the inner workings of the gemma-2b model.

1 Introduction

Figure 1: An illustration of a “logit” prism decomposing logit into different components (generated by DALL-E)

The logit lens (nostalgebraist 2020) is a simple yet powerful tool for understanding how transformer models (Vaswani et al. 2017; Brown et al. 2020) make decisions. In this work, we extend the logit lens approach in a mathematically rigorous and effective way. By treating certain parts of the network activations as constants, we can leverage the linear properties within the network to break down the logit output into individual component contributions. Using this principle, we introduce simple “prisms” for the residual stream, attention layers, and MLP layers. These prisms allow us to calculate how much each component contributes to the final logit output.

Our approach can be thought of as applying a series of prisms to the transformer network. Each prism in the sequence splits the logits from the previous prism into separate components. This enables us to see how different parts of the model—such as attention heads, MLP neurons, or input embeddings—influence the final output.

To showcase the power of our method, we present two illustrative examples:

• In the first example, we examine how the gemma-2b model performs the simple factual retrieval task of retrieving a capital city from a country name. Our findings suggest that the model learns to encode information about country names and their capital cities in a way that allows the network to easily convert country embeddings into capital city unembeddings through a linear projection.
• The second example explores how the gemma-2b model adds two small numbers (ranging from 1 to 9). We uncover interesting insights into the workings of MLP layers. The network predicts output numbers using interpretable templates learned by MLP neurons. When multiple neurons are activated simultaneously, their predictions interfere with each other, ultimately producing a final prediction that peaks at the correct number.

2 Method

See the method section at https://neuralblog.github.io/logit-prisms/#method 

3 Examples

In this section, we apply the prisms proposed earlier to explore how the gemma-2b model works internally in two examples. We use the gemma-2b model because it’s small enough to run on a standard PC without a dedicated GPU.

Retrieving capital city. First, let’s see how the model retrieves factual information to answer this simple question:

The capital city of France is ___

The model correctly predicts ▁Paris as the most likely next token. To understand how it arrives at this prediction, we’ll use the prisms from the previous section.

We start by using the residual prism to plot how much each layer contributes to the logit output for several candidate tokens (different capital cities). Comparing the prediction logit of the right answer to reasonable alternatives can reveal important information about the network’s decision process.

Figure 3 shows each layer’s logit contribution for multiple candidate tokens. Some strong signals stand out, with large positive and negative contributions in the first and last layers. These likely mean these layers play key roles in the model’s predictions. Interestingly, there’s a strong positive contribution at the start, followed by an equally strong negative contribution in the next layer (the first attention output). This might be because the gemma-2b model’s embedding and unembedding vectors are the same. So the input token strongly predicts itself as the output (due to the nature of the dot product operation). The network has to balance this out with a strong negative contribution in the next layer.

Figure 3 B zooms in to compare logit contributions at each layer for different targets. The 𝑎15 contribution stands out between ▁Paris and other candidates. At this layer, the attention output aligns much more with the unembedding vector of ▁Paris than other candidates.

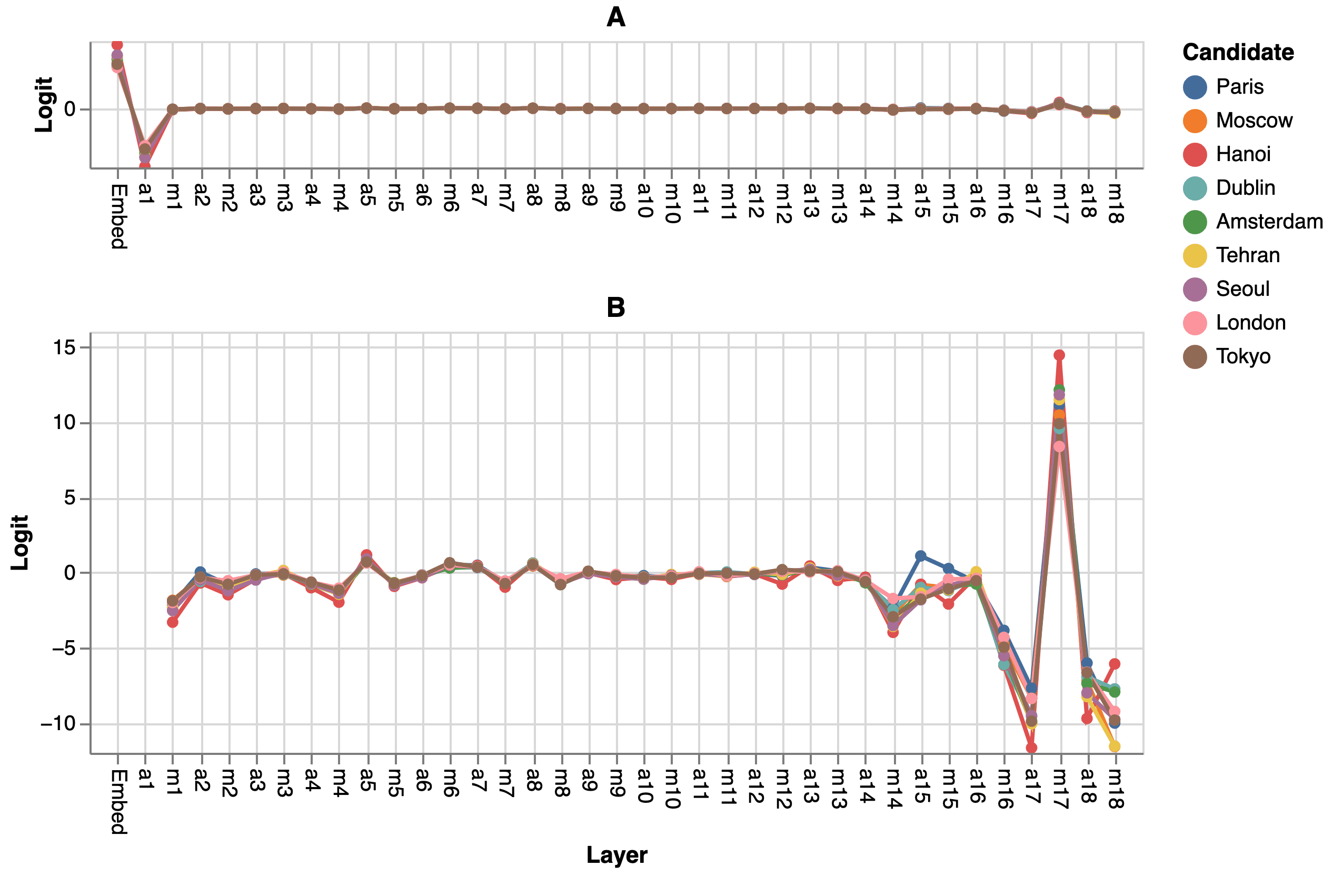
Figure 3: Logit contribution of each layer for different target tokens. Figure A shows the contributions of all layers, while Figure B zooms in on the contribution of the last layers.

We think 𝑎15 reads the correct output value from somewhere else via the attention mechanism, so we use the attention prism to decompose 𝑎15 into smaller pieces. Figure 4 shows how much each input token influences the output logits via the attention layer 15. The ▁France token heavily affects the output through attention head 6 of the layer, which makes very much sense as ▁France should somehow inform the network to output the correct capital city.

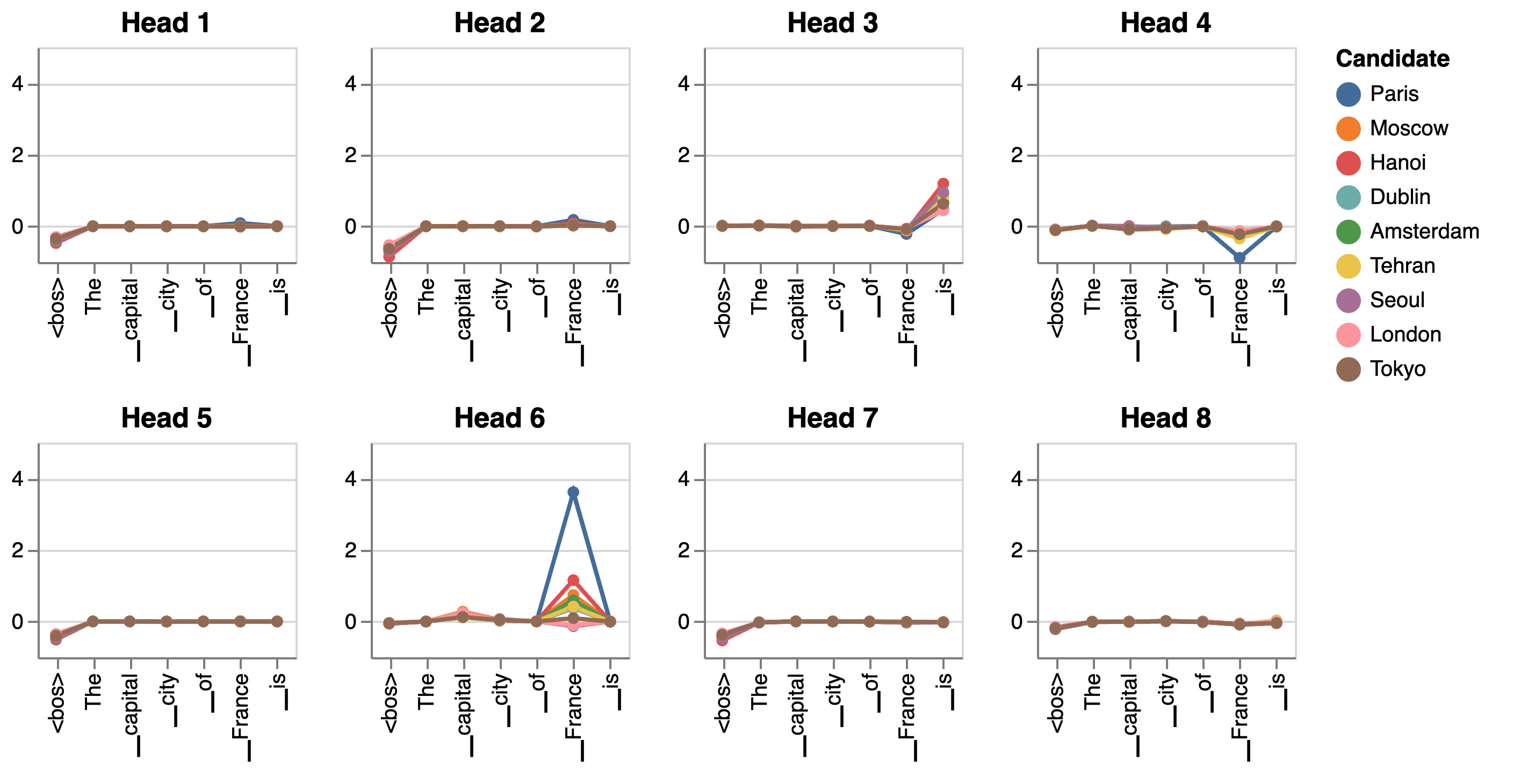
Figure 4: Logit contribution of each input token through attention heads at layer 15.

Next, we again use the residual prism to decompose the attention head 6 logits into smaller pieces. Figure 5 shows how the residual outputs from all previous layers at the ▁France token contribute to the output logit via attention head 6. Interestingly, the ▁France embedding vector contributes the most to the output logit. This indicates that the embedding vector of ▁France somehow already includes the information about its capital city, and this information can be read easily by attention head 6.

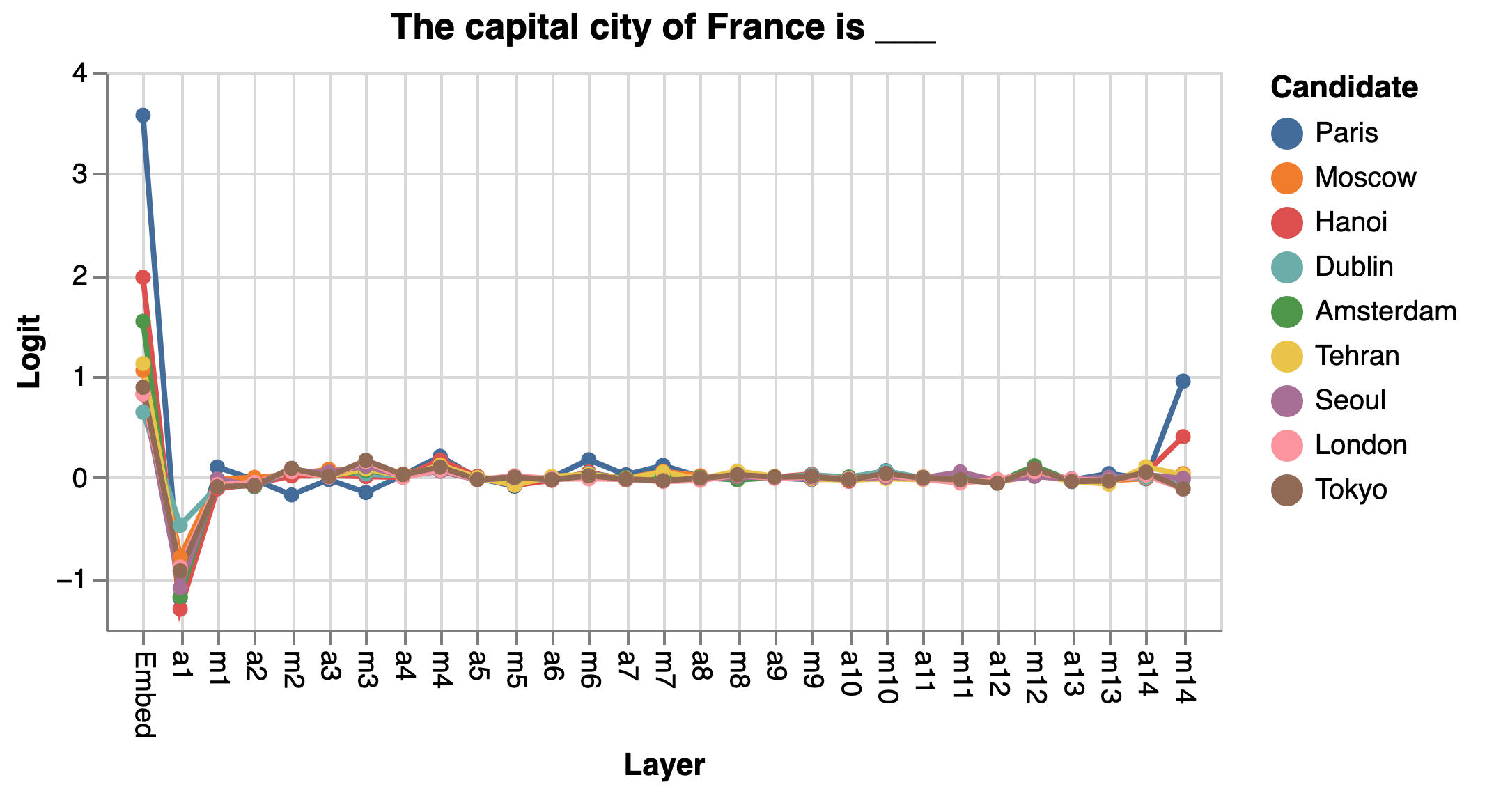
Figure 5: Logit contribution of all residual outputs through attention head 6 at layer 15.

One direct result of using prisms is that we have a linear projection that maps the ▁France embedding vector to capital city candidates’ unembedding vectors. We think this linear projection is meaningful not just for ▁France, but has similar effects on other country tokens too. To check this hypothesis, we apply the same projection matrix to other countries’ embedding vectors. Figure 6 shows the same matrix does indeed project other country names to their respective capitals.

This suggests that the network learns to represent country names and capital city names in such a way that it can easily transform a country embedding to the capital city unembedding using a linear projection. We hypothesize that this observation can be generalized to other relations encoded by the network as well.

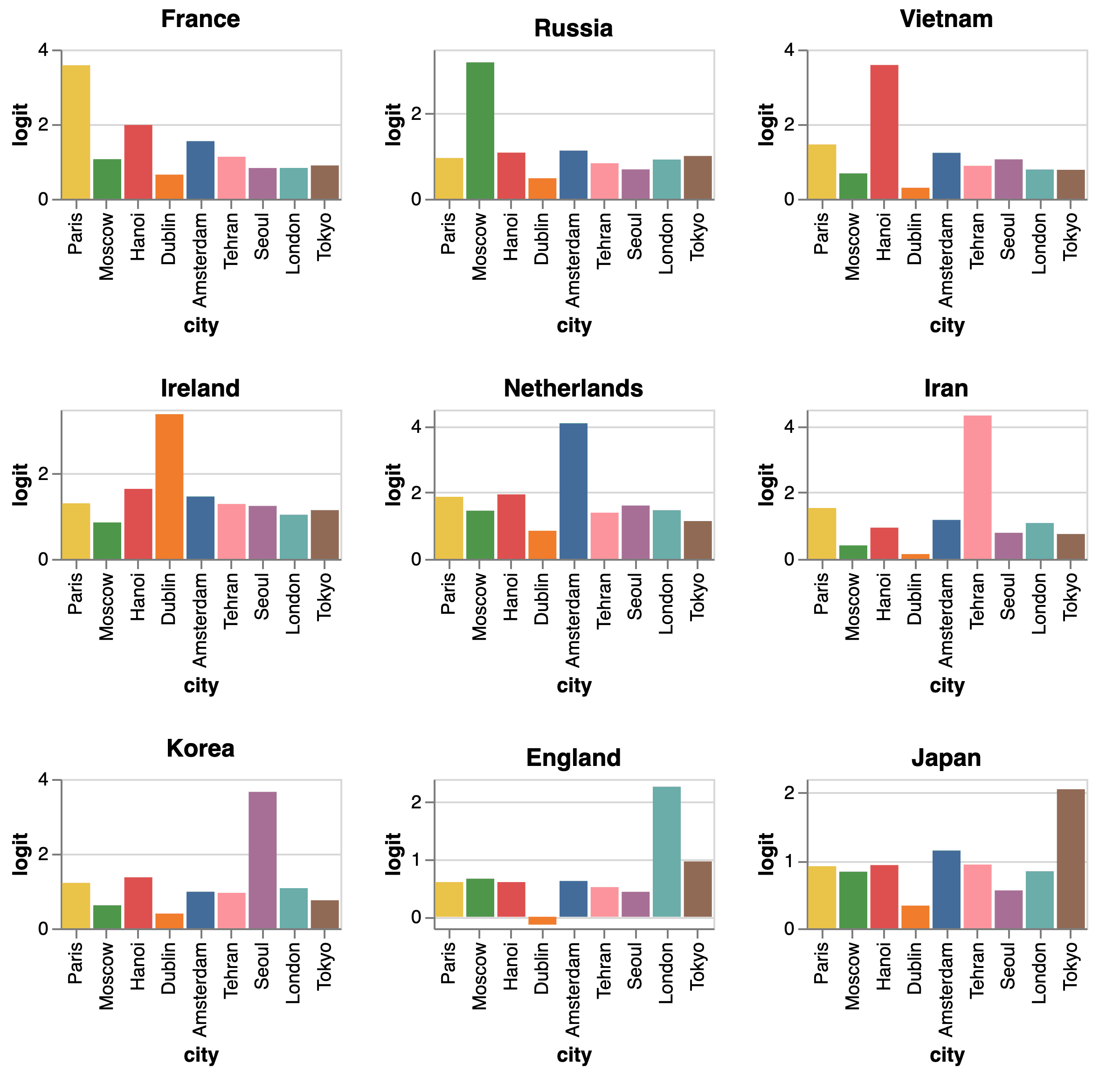
Figure 6: Linear projection from country embedding to capital city’s logit.

Digit addition. Let’s explore how gemma-2b performs arithmetic by asking it to complete the following:

7+2=_

The model correctly predicts 9 as the next token. To understand how it achieves this, we employ our prisms toolbox. First, using the residual prism, we decompose the residual stream and examine the contributions of different layers for target tokens ranging from 0 to 9 (Figure 7). The MLP layer at layer 16 (m16) stands out, predicting 9 with a significantly higher logit value than other candidates. This substantial gap is unique to m16, indicating its crucial role in the model’s prediction of 9.

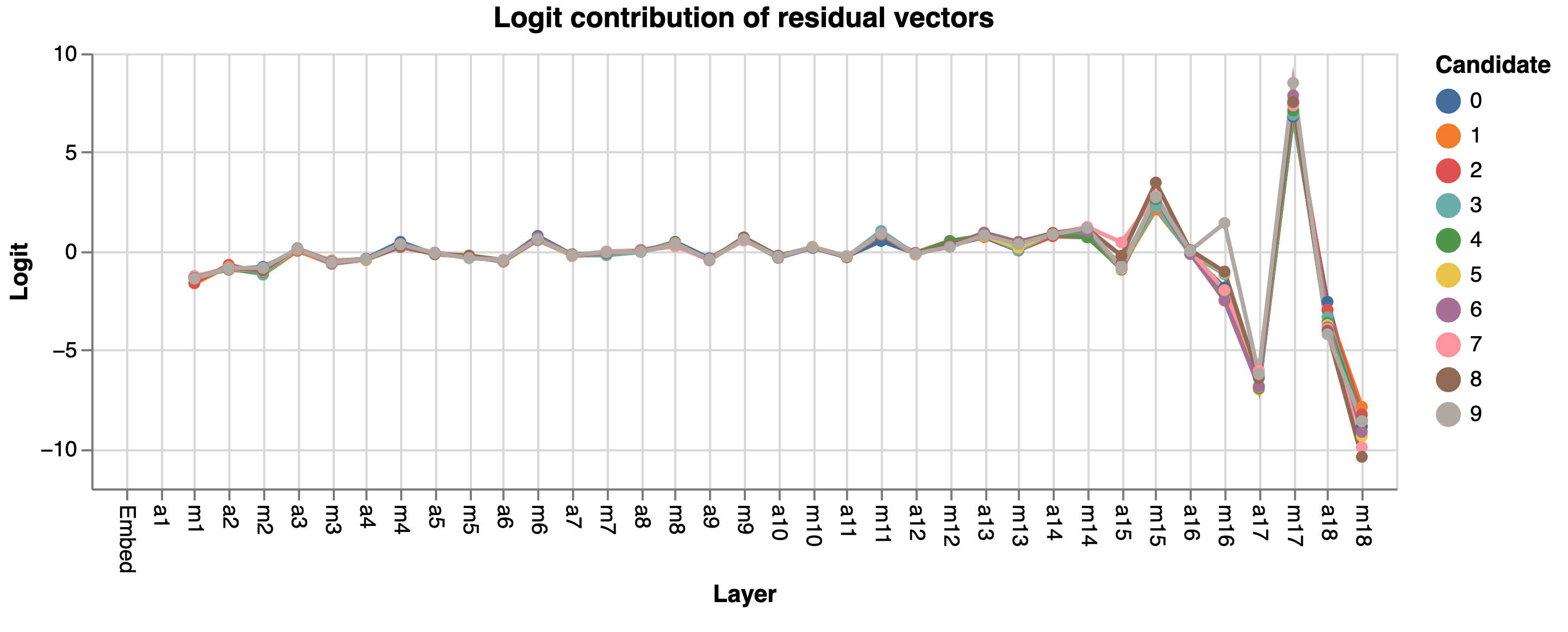
Figure 7: Contributions of different layers to the logit outputs of different candidates (from 0 to 9) using the residual prism.

Next, we use the MLP prism to identify which neurons in m16 drive this behavior. Decomposing m16 into contributions from its 16,384 neurons, we find that most are inactive. Extracting the top active neurons, we observe that they account for the majority of m16’s activity. Figure 8 shows these top neurons’ contributions to candidates from 0 to 9, revealing distinct patterns for each neuron. For example, neuron 10029 selectively differentiates odd and even numbers. Neuron 11042 selectively predicts 7, while neuron 12552 selectively avoids predicting 7. Neurons 15156 and 2363 show sine-wave patterns. While no single neuron dominantly predicts 9, the combined effect of these neurons’ predictions peaks at 9.

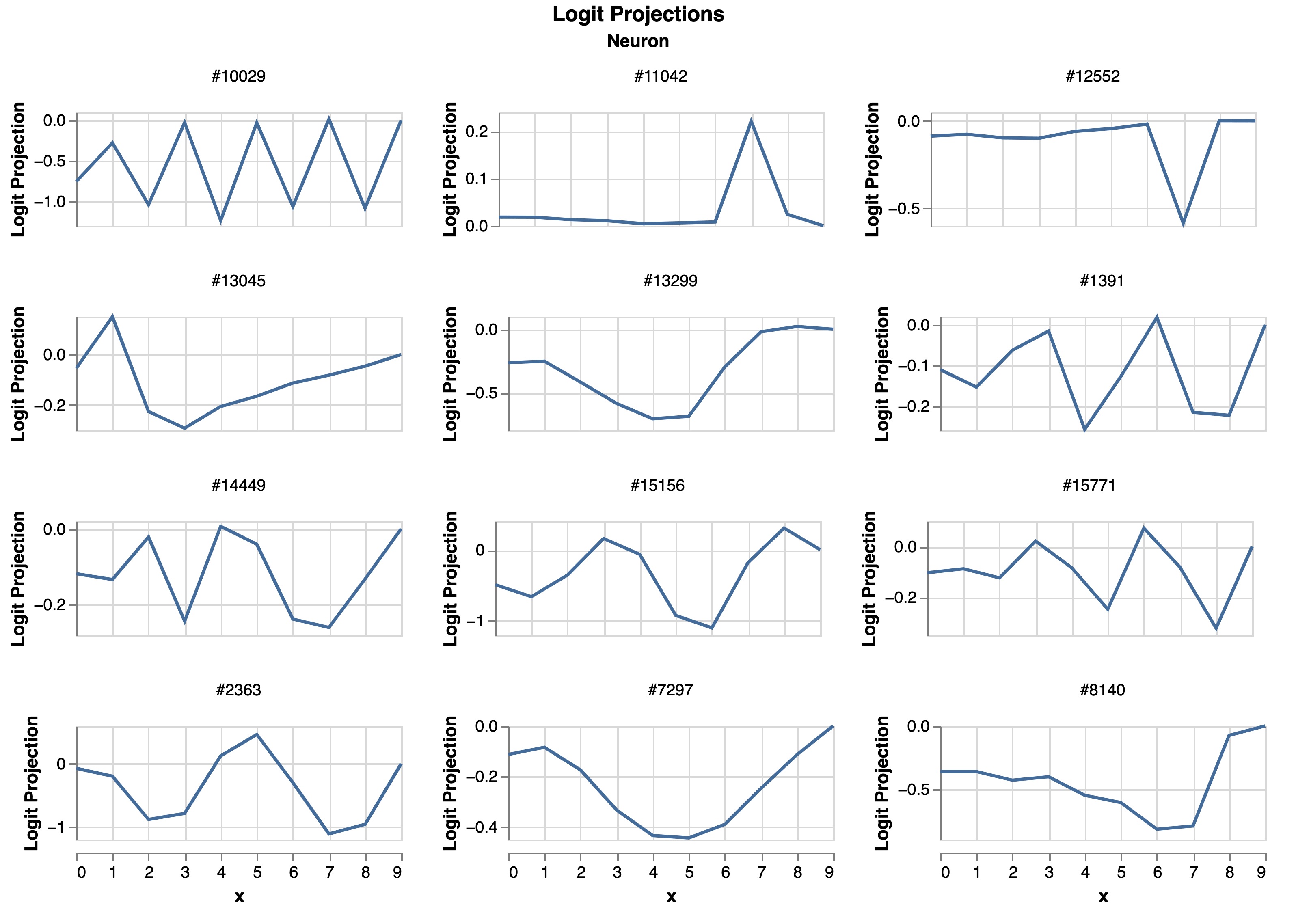
Figure 8: Top neuron contributions for different targets ranging from 0 to 9.

Note that the neurons’ contributions to the target logits are simply linear projections onto different target token unembedding vectors. The neuron activity patterns in Figure 8 are likely encoded in the target token unembeddings; as such, these patterns can be easily extracted using a linear projection. When we visualize the digit unembedding space in 2D (Figure 9), we discover that the numbers form a heart-like shape with reflectional symmetry around the 0-5 axis.

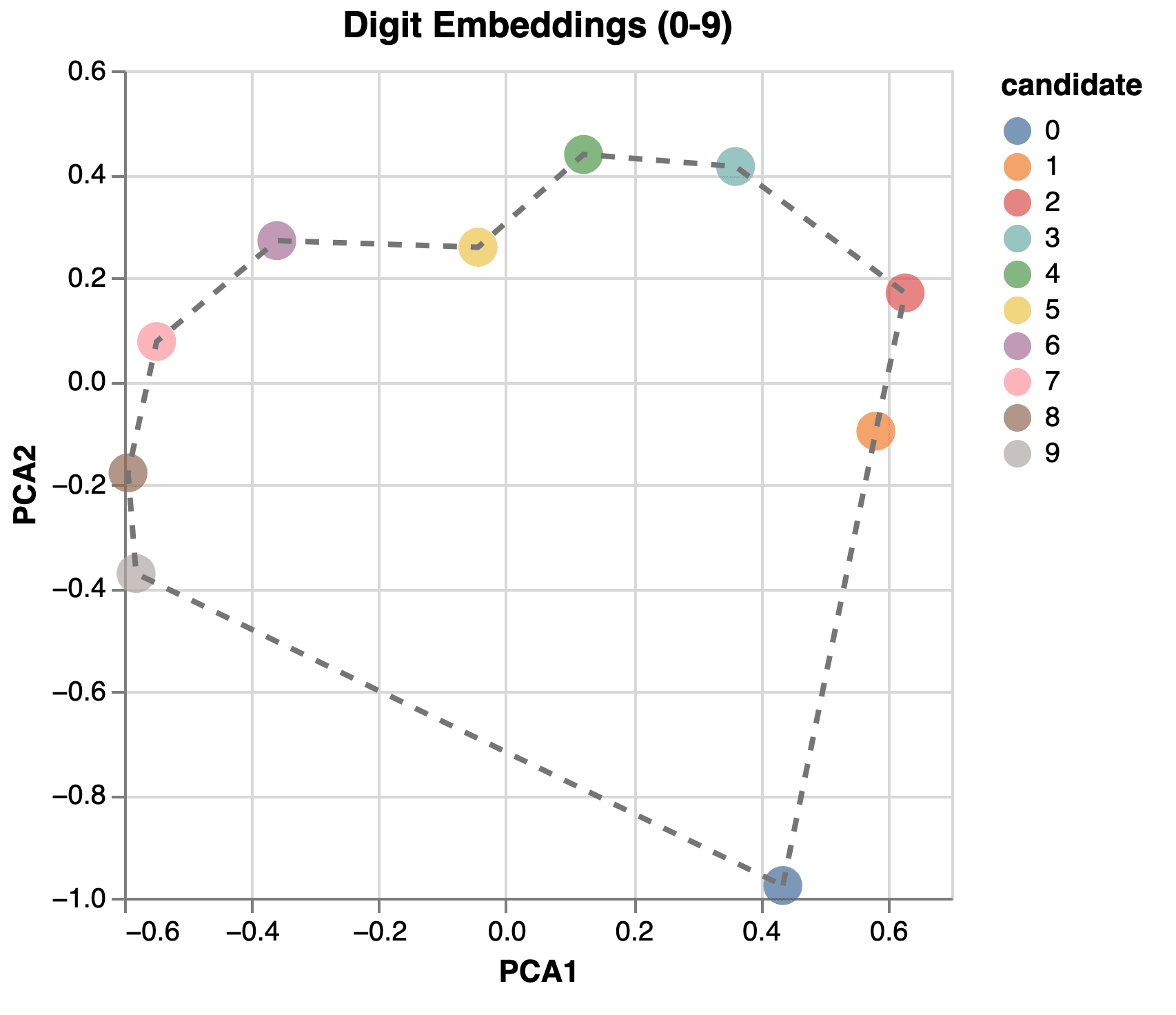
Figure 9: 2D projection of digit unembedding vectors. The embeddings are projected to 2D space using PCA. Each point represents a digit, and the points are connected in numerical order.

Our hypothesis is that transformer networks encode templates for outputs in the unembedding space. The MLP layer then selectively reads these templates based on their linear projection 𝑊down. By triggering a specific combination of neurons, each representing a template, the network ensures the logits reach their maximum value for the tokens with the highest probability.

4 Related Work

Our work builds upon and is inspired by several previous works. The logit lens method (nostalgebraist 2020) is closely related, allowing exploration of the residual stream in transformer networks by treating middle layer hidden states as the final layer output. This provides insights into how transformers iteratively refine their predictions. The author posits that decoder-only transformers operate mainly in a predictive space.

The tuned lens method (Belrose et al. 2023) improves upon the logit lens approach by addressing issues such as biased estimates and not working as well with some model families. Their key innovation is adding learnable parameters when reading logits from intermediate layers.

The path expansion trick used by (Elhage et al. 2021) decomposes one- and two-layer transformers into sums of different computation paths. Our approach is similar but treats each component independently to avoid combinatorial explosion in larger networks.

(Wang et al. 2022) examines GPT-2 circuits for the Indirect Object Identification task, using the last hidden state norm to determine each layer’s contribution to the output, similar to our residual prism. Their analysis of the difference in logits between candidates is, in fact, very similar to our candidate comparison.

Our findings in the example section align with previous research in several ways. (Mikolov et al. 2013) demonstrate that their Word2vec technique captures relationships between entities, such as countries and their capital cities, as directions in the embedding space. They show that this holds true for various types of relationships. This aligns with our observation of how the gemma-2b model represents country embeddings and capital city unembeddings.

Numerous studies (Zhang et al. 2021, 2024; Mirzadeh et al. 2023) have empirically observed sparse activations in MLP neurons, which is consistent with our MLP analysis. However, the primary focus of these works is on leveraging the sparsity to accelerate model inference rather than interpreting the model’s behavior.

(Geva et al. 2021) suggest that MLP layers in transformer networks act as key-value memories, where the 𝑊up matrix (the key) detects input patterns and the 𝑊down matrix (the value) boosts the likelihood of tokens expected to come after the input pattern. In our examples, we show that MLP neurons can learn understandable output templates for digit tokens. (Nanda et al. 2023) study how a simple 1-layer transformer network carries out modular addition task. They discover that the network’s MLP neurons use constructive interference of multiple output templates to shape the output distribution, making it peak at the right answer.

5 Conclusion

This paper introduces logit prisms, a simple but effective way to break down transformer outputs, making them easier to interpret. With logit prisms, we can closely examine how the input embeddings, attention heads, and MLP neurons each contribute to the final output. Applying logit prisms to the gemma-2b model reveals valuable insights into how it works internally.