What I can't figure out is how to specify possible worldstates “in the absence of an OP”.
Can we just replace the optimizer's output with random noise? For example, if we have an AI running in a black box, that only acts on the rest of the universe through a 1-gigabit network connection, then we can assign a uniform probability distribution over every signal that could be transmitted over the connection over a given time (all 2^(10^9) possibilities per second), and the probability distribution of futures that yields is our distribution over worlds that "could have been". We could do the same thing with a human brain and, say, all combinations of action potentials that could be sent down the spinal cord over a given time. This is desirable, because it separates optimization power from physical power. So paralyzed people aren't less intelligent just because "raise arm" isn't an option for them (That is, no combination of action potentials in their head will cause their arm to move).
More formally, an agent is a function or program that has a range or datatype. The range/datatype is the set of what we would call the agent's options. So assume we can generate counterfactual outcomes for each option in the range, the same way your favorite decision theory does. Then we can take optimization power to be the difference between EU given what the agent actually does, and the average EU over all the counterfactuals.*
If the OP is some kind of black-box AI agent, it's easier to imagine this. But if the OP is evolution, or a forest fire, it's harder to imagine.
I'm not so sure. Choosing to talk about natural selection as an agent means defining an agent which values self-replication and outputs a replicator. So if you have a way of measuring how good a genome is at replicating, you could just subtract from that how good a random sequence of base-pairs is, on average, at replicating, to get a measure of how much natural selection has optimized that genome. Of course, you could do the same thing with an entire animal versus a random clump of matter, because the range of the agent is just part of the definition.
EDIT: * AlexMennen had a much better idea for normalizing this than I did ;)
We considered random output as a baseline. It doesn't seem correct, to me.
1) You'd need a way to even specify the set of "output" of any possible OP. This seems hard to me because many OPs do not have clear boundaries or enumerable output channels, like forest fires or natural selection or car factories.
2) This is equal to a flat prior over your OPs outputs. You need some kind of specification for what possibilities are equally likely, and a justification thereof.
3) Even if we consider an AGI with well-defined output channels, it seems to me that random outputs are potentially very very very destructive, and therefore not the "default" or "status quo" against which we should measure.
I think the idea should be explored more, though.
1) You'd need a way to even specify the set of "output" of any possible OP. This seems hard to me because many OPs do not have clear boundaries or enumerable output channels, like forest fires or natural selection or car factories.
How do you define an optimization process without defining its output? If you want to think of natural selection as a force that organizes matter into self-replicators, then compare the reproductive ability of an organism to the reproductive ability of a random clump of matter, to find out how much natural selection has acted on it. If you want to think of it as a force that produces genomes, then compare an evolved genome to a random strand of DNA (up to some maximum length).
I can't think of a way of fitting a forest fire into this model either, which suggests it isn't useful to think of forest fires under this paradigm. But isn't that a good sign? If anything could be usefully modeled as an optimizer, wouldn't that hint that the concept is overly broad?
2) This is equal to a flat prior over your OPs outputs. You need some kind of specification for what possibilities are equally likely, and a justification thereof.
Why? Isn't the crux of the decision-making process pretending that you could choose any of your options, even though, as a matter of fact, you will choose one? I can see how you would run into some fuzziness if you tried to apply it to natural selection or even brains. But for the mathematical model, where the process selects from some abstract set of options, equal weighting seems appropriate. And this maps fairly straightforwardly onto an AI acting over a physical wire.
3) Even if we consider an AGI with well-defined output channels, it seems to me that random outputs are potentially very very very destructive, and therefore not the "default" or "status quo" against which we should measure.
(EDIT: D'oh! I just realized what you meant by random outputs being "destructive". You mean that if an AGI were to take its options to be "configurations of matter in the universe", then its baseline would be a randomly shuffled universe that was almost completely destroyed from our perspective. But I don't think this makes sense. Just because an AGI is smart enough to reorganize all matter in the universe doesn't mean that it makes sense for it to output decisions in that form. That would basically be a type error, just like if I were to decide "be in New York" instead of "drive to New York". The options the AGI has to choose from are outputs of a subroutine running inside of itself. So if it has a robot body, then the "default" or unoptimized output is random flailing about, or if it interacts through a text terminal, it would be printing random gibberish, most of which does nothing and leaves the configuration of the universe largely unchanged (and a few of which convince the programmer to give it access to the internet so it can take over the world.)).
Are you saying that an "AI" outputting random noise could do worse than an "AI" with optimization power measured at zero (i.e. zero intelligence)? Seems to me that, to reliably do worse than random, you would have to be trying to do badly. And you would have to be doing so with a strictly positive level of skill.
(Note: for a model of natural selection that might actually be usable in practice, suppose that we know a set X of mutations have occurred in a population over a given time, and that a subset of these X have become fixed in the population (the rest have been weeded out). To calculate how "optimized" X is, compare the reproductive fitness of the actual population to the average fitness of hypothetical populations which, instead of X*, had retained some random subset of the mutations from X (that is, selected with uniform probability from the power set of X). The measure of "reproductive fitness" could be as simple as population size.)
I can't think of a way of fitting a forest fire into this model either, which suggests it isn't useful to think of forest fires under this paradigm.
Forest fires are definitely OPs under my intuitive concept. They consistently select a subset of possible future (burnt forests). They're probably something like chemical energy minimizers; if I were to measure their efficacy, it would be something like number of carbon-based molecules turned into CO2. But the only reason we can come up with semi-formal measures like CO2 molecules or output on wires is because we're smart human-things. I want to figure out how to algorithmically measure it.
Isn't the crux of the decision-making process pretending that you could choose any of your options, even though, as a matter of fact, you will choose one?
Yes. But what does "could" mean? It doesn't mean that you they all have equal probability. If literally all you know is that there are n outputs, then giving them 1/n weight is correct. But we usually know more, like the fact that it's an AI, and it's unclear how to update on this.
Are you saying that an "AI" outputting random noise could do worse than an "AI" with optimization power measured at zero (i.e. zero intelligence)?
Absolutely. Like how random outputs of a car cause it to jerk around and hit things, whereas a zero-capability car just sits there. Also, we're averaging over all possible outputs with equal weights. Even if most outputs are neutral or harmless, there are usually more damaging outputs than good ones. It's generally easier to harm than destroy. The more powerful actuators the AI has, the most damage random outputs will do.
Thanks for all your comments!
Oops, looks like I was wrong about what you meant (ignore the edit). But yes, if you give a stupid thing lots of power you should expect bad outcomes. A car directed with zero intelligence is not a car sitting still, but precisely what you said was dangerous: a car having its controls blindly fiddled with. But if you just run a stupid program on a computer, it will never acquire power in the first place. Most decisions are neutral, unless they just happen to be plugged into something that has already been optimized to have large physical effects (like a bulldozer). Of those decisions that do have large effects, most will be destructive, but that's exactly what we should expect from a stupid optimization process acting on something that has already been finely honed by a smart optimization process.
what does "could" mean?
Good question. I think it has something to do with simply defining some set of actions to be your "options", and temporarily putting all your options on an equal footing, so that you end up with the one with the best consequences, rather than the one that seemed like the one you'd be most likely to choose. I don't think it even has much to do with probabilities, because then you run into self-fulfilling prophesies - doing what you predicted you'd do, thereby justifying the prediction.
In this case, we want to measure how good an agent did, relative to how it could have done. That is, how good were the consequences of the option it chose, relative to its other options. I don't see any reason to weight those options according to a probability distribution, unless you know what "half an option" means. And choosing a distribution poses huge problems. After all, we know the agent chose one of the options with probability 1.0, and all the others with probability 0.0.
Forest fires are definitely OPs under my intuitive concept. They consistently select a subset of possible future (burnt forests).
Well, you could just compare the rate of oxidation under a flame, to the average rate of oxidation of all surfaces (including those that happen to be on fire) within whichever reference class you prefer. (I think choosing a reference class (set of options) is just part of how you define the OP. And you just define the OP whichever way helps you understand the world best.)
Thanks for all your comments!
Is this actually helpful? I try to read up on the background for this stuff, but I never know if I'm just rehashing what's already been discussed, and if so, whether reviewing that here would be useful to anyone.
So paralized people aren't less intelligent just because "raise arm" isn't an option for them (That is, no combination of action potentials in their head will cause their arm to move).
Caveat: if someone is paralyzed because of damage to their brain, rather than to their peripheral nerves or muscles, then this is not true, which creates and undesirable dependency of the measured optimization power on the location of the cause of the disability. Despite this drawback, I like this formalization.
Erm, you probably want to use something like (EU - EU[av]) / EU[av], where EU is just the actual expected utility, and EU[av] is the average of the expected utilities of the counterfactual probability distributions over world states associated with each of the agents options.
No, that clearly makes no sense if EU[av] <= 0. If you want to divide by something to normalize the measured optimization power (so that multiplying the utility function by a constant doesn't change the optimization power), the standard deviation of the expected utilities of the counterfactual probability distributions over world states associated with each of the agent's options would be a better choice.
Caveat: if someone is paralyzed because of damage to their brain, rather than to their peripheral nerves or muscles, then this is not true,
That's why I specified that the you don't get penalized for disabilities that have nothing to do with the signals leaving your brain.
which creates and undesirable dependency of the measured optimization power on the location of the cause of the disability.
I disagree. I think that's kind of the point of defining "optimization power" as distinct from "power". A man in a prison cell isn't less intelligent just because he has less freedom.
No, that clearly makes no sense if EU[av] <= 0. If you want to divide by something to normalize the measured optimization power (so that multiplying the utility function by a constant doesn't change the optimization power), the standard deviation of the expected utilities of the counterfactual probability distributions over world states associated with each of the agent's options would be a better choice.
Great idea! I was really sloppy about that, realized at the last minute that taking a ratio was clearly wrong, and just wanted to make sure that you couldn't get different answers by scaling the utility function. I guess |EU[av]| does that, but now we can get different answers by shifting the utility function, which shouldn't matter either. Standard deviation is infinitely better.
There's a big field associated with optimisation. They use metrics like number of trials, time taken, resources used and the quality of the solution to measure the relative worth of optimisation processes. The size of the target relative to the size of the search space typically isn't used - because the search space is often unbounded, and the size of the target is usually pretty irrelevant. Of course, all this has been explained before.
It's confusing that OP stands for two different concepts: "optimization process" and "optimization power."
My first reaction (which I still mostly endorse): KISS; OP = EU' is fine.
I do not share your intuition for criterion 2, because exponentially increasing utility should be achievable, but only because increasing optimization power is, so it seems desirable that constant OP yields subexponential growth in EU, and exponential growth in OP yields exponential growth in EU.
At least for humans, there is an intuitive sign to utility. We wouldn't say that stubbing your toe is 1,000,000 utils, and getting a car is 1,002,000 utils. It seems to me, especially after reading Omohundro's “Basic AI Drives”, that there is in some sense an intrinsic zero utility for all OPs.
Disagree. When we talk about the utility of stubbing your toe, we mean the change in utility from what it would have been if you hadn't stubbed your toe. Obviously this is going to be negative, but that doesn't put a zero point on your entire utility function.
In your last big paragraph, you seem to be confusing utility of the current world-state with resources with which to increase the utility of future world-states. They are different.
That said, if you need to call some certain amount of utility "zero", your suggestion of using the utility of whatever would happen without the agent existing does seem to hold merit. (or similarly: expected utility if the agent chooses actions randomly).
Although I still don't much like OP = EU'/|EU|, it does have some desirable properties. While I don't like the dependence on origin (singularity at zero = nasty), it nicely breaks the dependence on scale. And I don't think the presence of absolute values in the equation is all that bad; in fact, it neatly parallels the fact that utility functions can be multiplied only by positive scales while remaining equivalent.
The negative optimization power question is interesting. The zero-point of nonexistence seems totally legit, and I haven't thought about it in that much detail before.
My intuition would be that negative optimization power reflects actively working against your values whenever you try anything, which definitely seems like it should be possible. Like, if I were an entity which launched a bomb at whatever I was trying to pay attention to, I would probably be negatively optimizing.
If you try and extrapolate through nonexistence as the zero though, things get weird. Negative optimization power then seems to reflect being an entity that the world is actively trying to prevent. At first glance that's odd, but that also makes quite a bit of sense if you assume that the world contains other agents who might try to prevent you from doing things.
which definitely seems like it should be possible.
Yeah, this normal type of negative OP is possible with OP = EU'/|EU| and EU positive but decreasing. I'm worried about the weirdness of decreasing and negative EU.
In explorations of AI risk, it is helpful to formalize concepts. One particularly important concept is intelligence. How can we formalize it, or better yet, measure it? “Intelligence” is often considered mysterious or is anthropomorphized. One way to taboo “intelligence” is to talk instead about optimization processes. An optimization process (OP, also optimization power) selects some futures from a space of possible futures. It does so according to some criterion; that is, it optimizes for something. Eliezer Yudkowsky spends a few of the sequence posts discussing the nature and importance of this concept for understanding AI risk. In them, he informally describes a way to measure the power of an OP. We consider mathematical formalizations of this measure.
Here's EY's original description of his measure of OP.
Put a measure on the state space - if it's discrete, you can just count. Then collect all the states which are equal to or greater than the observed outcome, in that optimization process's implicit or explicit preference ordering. Sum or integrate over the total size of all such states. Divide by the total volume of the state space. This gives you the power of the optimization process measured in terms of the improbabilities that it can produce - that is, improbability of a random selection producing an equally good result, relative to a measure and a preference ordering.
If you prefer, you can take the reciprocal of this improbability (1/1000 becomes 1000) and then take the logarithm base 2. This gives you the power of the optimization process in bits.
Let's say that at time we have a formalism to specify all possible world states
we have a formalism to specify all possible world states  at some future time
at some future time  . Perhaps it is a list of particle locations and velocities, or perhaps it is a list of all possible universal wave functions. Or maybe we're working in a limited domain, and it's a list of all possible next-move chess boards. Let's also assume that we have a well-justified prior
. Perhaps it is a list of particle locations and velocities, or perhaps it is a list of all possible universal wave functions. Or maybe we're working in a limited domain, and it's a list of all possible next-move chess boards. Let's also assume that we have a well-justified prior ) over these states being the next ones to occur in the absence of an OP (more on that later).
over these states being the next ones to occur in the absence of an OP (more on that later).
We order according to the OP's preferences. For the moment, we actually don't care about the density, or “measure” of our ordering. Now we have a probability distribution over
according to the OP's preferences. For the moment, we actually don't care about the density, or “measure” of our ordering. Now we have a probability distribution over  . The integral from
. The integral from  to
to  over this represents the probability that the worldstate at
over this represents the probability that the worldstate at  will be better than
will be better than  , and worse than
, and worse than  . When time continues, and the OP acts to bring about some worldstate
. When time continues, and the OP acts to bring about some worldstate  , we can calculate the probability of an equal or better outcome occurring;
, we can calculate the probability of an equal or better outcome occurring;
This is a simple generalization of what EY describes above. Here are some things I am confused about.
Finding a specification for all possible worldstates is hard, but it's been done before. There are many ways to reasonably represent this. What I can't figure out is how to specify possible worldstates “in the absence of an OP”. This phrase hides tons of complexity. How can we formally construct this counterfactual? Is the matter that composes the OP no longer present? Is it present but “not acting”? What constitutes a null action? Are we considering the expected worldstate distribution as if the OP never existed? If the OP is some kind of black-box AI agent, it's easier to imagine this. But if the OP is evolution, or a forest fire, it's harder to imagine. Furthermore, is the specification dualist, or is the agent part of the worldstates? If it's dualist, this is a fundamental falseness which can have lots of bad implications. If the agent is part of the worldstates, how do we represent them “in absence of an OP”?
But for the rest of this article, let's pretend we have such a specification. There's also a loss from ignoring the cardinal utility of the worldstates. Let's say you have the two distributions of utility over sets , representing two different OPs. In both, the OP choose a
, representing two different OPs. In both, the OP choose a  with the same utility
with the same utility 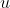 . The distributions are the same on the left side of
. The distributions are the same on the left side of 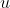 , and the second distribution has a longer tail on the right. It seems like the OP in distribution 1 was more impressive; the second OP missed all the available higher utility. We could make the expected utility of the second distribution arbitrarily high, while maintaining the same fraction of probability mass above the achieved worldstate. Conversely, we could instead extend the left tail of the second distribution, and say that the second OP was more impressive because it managed to avoid all the bad worlds.
, and the second distribution has a longer tail on the right. It seems like the OP in distribution 1 was more impressive; the second OP missed all the available higher utility. We could make the expected utility of the second distribution arbitrarily high, while maintaining the same fraction of probability mass above the achieved worldstate. Conversely, we could instead extend the left tail of the second distribution, and say that the second OP was more impressive because it managed to avoid all the bad worlds.
Perhaps it is more natural to consider two distributions; the distribution of utility over entire world futures assuming the OP isn't present, versus the distribution after the OP takes its action. So instead of selecting a single possibility with certainty, the probabilities have just shifted.
How should we reduce this distribution shift to a single number which we call OP? Any shift of probability mass upwards in utility should increase the measure of OP, and vice versa. I think also that an increase in the expected utility (EU) of these distributions should be measured as a positive OP, and vice versa. EU seems like the critical metric to use. Let's generalize a little further, and say that instead of measuring OP between two points in time, we let the time difference go to zero, and measure instantaneous OP. Therefore we're interested in some equation which has the same sign as
Besides that, I'm not exactly sure which specific equation should equal OP. I seem to have two contradicting desires;
1a) The sign of should be the sign of the OP.
should be the sign of the OP.
b) Negative and
and  should be possible.
should be possible.
2) Constant positive OP should imply exponentially increasing .
.
Criterion 1) feels pretty obvious. Criterion 2) feels like a recognition of what is “natural” for OPs; to improve upon themselves, so that they can get better and better returns. The simplest differential equation that represents positive feedback yields exponentials, and is used across many domains because of its universal nature.
This intuition certainly isn't anthropocentric, but it might be this-universe biased. I'd be interested in seeing if it is natural in other computable environments.
If we just use , then criterion 2) is not satisfied. If we use
, then criterion 2) is not satisfied. If we use  , then decreases in EU are not defined, and constant EU is negative infinite OP, violating 1). If we use
, then decreases in EU are not defined, and constant EU is negative infinite OP, violating 1). If we use  , then 2) is satisfied, but negative and decreasing EU give positive OP, violating 1a). If we use
, then 2) is satisfied, but negative and decreasing EU give positive OP, violating 1a). If we use  , then 2) is still satisfied, but
, then 2) is still satisfied, but  gives
gives  , violating 1a). Perhaps the only consistent equation would be
, violating 1a). Perhaps the only consistent equation would be  . But seriously, who uses absolute values? I can't recall a fundamental equation that relied on them. They feel totally ad hoc. Plus, there's this weird singularity at
. But seriously, who uses absolute values? I can't recall a fundamental equation that relied on them. They feel totally ad hoc. Plus, there's this weird singularity at  . What's up with that?
. What's up with that?
Classically, utility is invariant up to positive affine transformations. Criterion 1) respects this because the derivative removes the additive constant, but 2) doesn't. It is still scale invariant, but it has an intrinsic zero. This made me consider the nature of “zero utility”. At least for humans, there is an intuitive sign to utility. We wouldn't say that stubbing your toe is 1,000,000 utils, and getting a car is 1,002,000 utils. It seems to me, especially after reading Omohundro's “Basic AI Drives”, that there is in some sense an intrinsic zero utility for all OPs.
All OPs need certain initial conditions to even exist. After that, they need resources. AIs need computer hardware and energy. Evolution needed certain chemicals and energy. Having no resources makes it impossible, in general, to do anything. If you have literally zero resources, you are not a "thing" which "does". So that is a type of intrinsic zero utility. Then what would having negative utility mean? It would mean the OP anti-exists. It's making it even less likely for it to be able to start working toward its utility function. What would exponentially decreasing utility mean? It would mean that it is a constant OP for the negative of the utility function that we are considering. So, it doesn't really have negative optimization power; if that's the result of our calculation, we should negate the utility function, and say it has positive OP. And that singularity at ? When you go from the positive side, getting closer and closer to 0 is really bad, because you're destroying the last bits of your resources; your last chance of doing any optimization. And going from negative utility to positive is infinite impressive, because you bootstrapped from optimizing away from your goal to optimizing toward your goal.
? When you go from the positive side, getting closer and closer to 0 is really bad, because you're destroying the last bits of your resources; your last chance of doing any optimization. And going from negative utility to positive is infinite impressive, because you bootstrapped from optimizing away from your goal to optimizing toward your goal.
So perhaps we should drop the part of 1b) that says negative EU can exist. Certainly world-states can exist that are terrible for a given utility function, but if an OP with that utility function exists, then the expected utility of the future is positive.
If this is true, then it seems there is more to the concept of utility than the von Neumann-Morgenstern axioms.
How do people feel about criterion 2), and my proposal that ?
?