I'm pretty sure we've had this anti-Newcomb problem discussion already. Short version: what this is is a constructive proof that any decision algorithm has to lose on some problems, because Omega could diagonalize against any algorithm, and then any agent implementing that algorithm is hosed. Therefore, it is fruitless to demand that a good decision algorithm or good agent never lose on any problems - one needs a more generous criterion of goodness. As for XDT, I don't see why it shouldn't get the $1M when playing an anti-Newcomb problem. 1,000,000 is bigger than 1,000, after all.
I'm not totally sure why you need the further hardware in this post either. From what I can tell, the real trouble is that logical implication is not what you want here - we're still waiting on a reasonable system of logical counterfactuals. 3, 4', and if I understand it right, 5, are just not addressing that core problem.
Hi Manfred, thx for commenting!
...what this is is a constructive proof that any decision algorithm has to lose on some problems, because Omega could diagonalize against any algorithm, and then any agent implementing that algorithm is hosed.
See my reply to KnaveOfAllTrades.
As for XDT, I don't see why it shouldn't get the $1M when playing an anti-Newcomb problem. 1,000,000 is bigger than 1,000, after all.
Which anti-Newcomb problem? In the XDT anti-Newcomb problem, 1000 is the maximal payoff. No decision theory gets more. In the UDT anti-Newcomb problem, XDT gets 1,000,1000 while UDT remains with 1,000,000.
...we're still waiting on a reasonable system of logical counterfactuals. 3, 4', and if I understand it right, 5, are just not addressing that core problem.
Well, there is more than one remaining problem :) Regarding logical counterfactuals, I think that the correct approach is going to be via complexity theory. Hope to write about it later, in the meanwhile you can check out this. By now I discovered some problems with the formalism I used there (and a possible path to fixing them), but I think the general direction is right.
As for XDT, I don't see why it shouldn't get the $1M when playing an anti-Newcomb problem. 1,000,000 is bigger than 1,000, after all.
Which anti-Newcomb problem? In the XDT anti-Newcomb problem, 1000 is the maximal payoff. No decision theory gets more.
Right, the XDT ANP. Because this is in fact a decision-controlled problem, only from the perspective of an XDT agent. And so they can simply choose to receive $1M on this problem if they know that that's what they're facing. $1M being bigger than $1000, I think they should do so.
But you do raise a good point, which is that there might be some way to avoid being beaten by other agents on decision-controlled problems, if you give up on maximizing payoff. It might depend on what metric of success you optimize the the decision procedure for. If you take the view logically upstream of filling the boxes, the maximum is $1.001M, and success is relative to that. If you take the view downstream, you might be satisfied with $1000 because that's the maximum.
Right, the XDT ANP. Because this is in fact a decision-controlled problem, only from the perspective of an XDT agent.
It is decision-determined from the perspective of any agent. The payoff only depends on the agent's decision: namely, it's 1000$ for two-boxing and 0$ for one-boxing.
And so they can simply choose to receive $1M on this problem if they know that that's what they're facing. $1M being bigger than $1000, I think they should do so.
Look on the problem from the perspective of the precursor. The precursor knows XDT two-boxes on the problem. There is no way to change this fact. So one box is going to be empty. Therefore building an XDT agent in this situation is no worse than building any other agent.
It is decision-determined from the perspective of any agent. The payoff only depends on the agent's decision: namely, it's 1000$ for two-boxing and 0$ for one-boxing.
Yeah, sorry, I misspoke. The contents of the boxes are controlled by the agent's decision, only for an XTD agent.
Look on the problem from the perspective of the precursor. The precursor knows XDT two-boxes on the problem. There is no way to change this fact. So one box is going to be empty. Therefore building an XDT agent in this situation is no worse than building any other agent.
I am using XDT here in the sense of "the correct decision algorithm (whatever it is)." An XDT agent, if faced with the XDT-anti-Newcomb-problem, can, based on its decision, either get $1M, or $1k. If it takes the $1M, it loses in the sense that it does worse on this problem than a CDT agent. If it takes the $1k, it loses in the sense that it just took $1k over $1M :P
And because of XDT's decision controlling the contents of the box, when you say "the payoff is $1000 for two-boxing and $0 for one-boxing," you're begging the question about what you think the correct decision algorithm should do.
And because of XDT's decision controlling the contents of the box, when you say "the payoff is $1000 for two-boxing and $0 for one-boxing," you're begging the question about what you think the correct decision algorithm should do.
The problem is in the definition of "correct". From my point of view, "correct" decision algorithm means the algorithm that a rational precursor should build. That is, it is the algorithm instantiating which by the precursor will yield at least as much payoff as instantiating any other algorithm.
Well, I agree with you there :P But I think you're cashing this out as the fixed point of a process, rather than as the maximization I am cashing it out as.
I didn't follow everything in the post, but it seems like the motivating problem is that UDT fails in an anti-Newcomb problem defined in terms of the UDT agent. But this sounds a lot like a fully general counterargument against decision algorithms; for any algorithm, we can form a decision problem that penalizes exactly that and only that agent. Take any algorithm running on a physical computer and place it in a world where we specify, as an axiom, that any physical instantiation of that algorithm is blasted by a proton beam as soon as it begins to run, before it can act. This makes any algorithm look bad, but this is just a no free lunch argument that every algorithm seems to fail in some worlds, especially ones where the deck is stacked against the algorithm by defining it to lose.
A decision process 'failing' in some worlds is a problem only if there exists some other decision process that does not suffer analogously. (Possible open problem: What do we mean by analogous failure or an analogously stacked world?)
Of course, it's possible this objection is headed off later in the post where I start to lose the train of thought.
Hi KnaveOfAllTrades, thx for commenting!
Your proton beam problem is not decision-determined in the sense of Yudkowsky 2010. That is, it depends directly on the decision algorithm rather than depending only on the decisions it makes. Indeed it is impossible to come up with a decision theory that is optimal for all problems, but it might be possible to come up with a decision theory that is optimal for some reasonable class of problems (like decision-determined problems).
Now, there is a decision-determined version of your construction. Consider the following "diagonal" problem. The agent makes a decision out of some finite set. Omega runs a simulation of XDT and penalizes the agent iff its decision is equal to XDT's decision.
This is indeed a concern for deterministic agents. However, if we allow the decision algorithm access to an independent source of random bits, the problem is avoided. XDT produces all answers distributed uniformly and gets optimal payoff.
This is indeed a concern for deterministic agents. However, if we allow the decision algorithm access to an independent source of random bits, the problem is avoided. XDT produces all answers distributed uniformly and gets optimal payoff.
Omega can predict the probability distribution on the agent answers, and it is possible to construct a Newcomb-like problem that penalizes any specific distribution.
Hi V_V, thx for commenting!
In a Newcomb-like problem, Omega copies the agent and runs it many times to measure the decision distribution. It then penalizes the agent if the distribution matches an explicitly given one. Such a problem is easily solved by the agent since it knows which distribution to avoid.
In an anti-Newcomb-like problem, Omega measures the distribution produced by XDT and compares it with the agent's decision. It then penalizes the agent according to the likelihood of its decision in the distribution. However, if XDT produces a uniform distribution, all agents do equally well.
A trickier diagonalization is a hybrid Newcomb-anti-Newcomb (NAN) problem. Omega copies the agent and runs it multiple times to measure the distribution. It then compares the result with a similar procedure applied to XDT and penalizes the agent if there is a close match.
Now, the NAN diagonalization can be solved if we assume the agent has access to random bits which are common between all of its copies but inaccessible by the rest of the universe (Omega). This assumption can be interpreted to mean the precursor gives the agent a randomly generated "password" before Omega copies it.
Now, the NAN diagonalization can be solved if we assume the agent has access to random bits which are common between all of its copies but inaccessible by the rest of the universe (Omega). This assumption can be interpreted to mean the precursor gives the agent a randomly generated "password" before Omega copies it.
Sure, but this defeats the purpose of Omega being a predictor.
Not really. The idea is looking for a decision theory that performs optimally a natural class of problems which is as wide as possible. CDT is optimal for action-determined problems, UDT is supposed to be optimal for decision-determined problems. Allowing this use of randomness still leaves us with a class of problems much wider than action-determined: for example the Newcomb problem!
Hi V_V, thx for commenting!
In Newcomb-like problems (i.e. when Omega copies the source code of the agent) you can penalize any specific distribution but the agent can always choose to produce a different distribution (because it knows which distribution is penalized).
In anti-Newcomb-like problems (i.e. when Omega uses hardcoded XDT) the payoff depends on a single decision rather than a distribution.
Your "UDT anti-Newcomb problem" reminds me of an open problem with TDT/UDT that was identified in the early days and still unsolved AFAIK. See the discussion here, but in short, it was pointed out that if most of the agents in the universe/multiverse are going to be UDT agents, they should be willing to play C in a one-shot PD game against a random agent sampled from the universe/multiverse. But human beings are not yet UDT agents, so it might be better to build some other kind of agent so we (or our successors) can play D instead. The approach suggested here looks like it could be relevant to solving that problem. What do you think?
One thing that worries me here is that if A has more computing power than P, it can compute P's actual output just by simulating it, so with the equations given in this post, you'd have to define how to condition the expectation of U() on statements that are known by the agent to be false. I was hoping that this is not actually a problem that needs to be solved in order to solve decision theory.
Hi Wei Dai, thx for commenting!
The "game of 3" problem indeed seems related. Apparently my decision theories solve it correctly, if we consider the precursor to be the "AI submitter". The discussion there is of enormous size, can you please point out the part about most of the agents in the multiverse?
Regarding successor-simulating-precursor, I think that any way of applying logical uncertainty that solves logical counterfactual mugging should handle this as well, since the precursor's "Tegmark V" should be preserved by the successor in some sense, and the precursor cannot simulate itself (see also this).
A possible solution is evaluating the expectation value at a depth of analysis (reference amount of computing resources) corresponding to the precursor's computing power. This doesn't mean the successor's superior computing power is wasted since it allows for more exhaustive maximization. In case of equation (4') the extra power is also used for evaluating pi.
Need to think more on this!
Apparently my decision theories solve it correctly, if we consider the precursor to be the "AI submitter".
Can you go into some detail on how your decision theories solve it?
The discussion there is of enormous size, can you please point out the part about most of the agents in the multiverse?
I guess it wasn't mentioned explicitly in that discussion, but it's how I've come to think of the problem. Perhaps the most relevant part of that discussion is Eliezer's direct reply, here.
Can you go into some detail on how your decision theories solve it?
Your problem can be written as
%20=%20\frac{1}{3}(PD_\alpha(A,%20B_1(A))+PD_\alpha(A,B_2(A))))
where and
are Omega's players,
) is your player and
is the payoff of the first player in the Prisoner Dilemma with the (1,5,6) payoff matrix.
Omega's players end up playing C regardless of . The agent can either understand this or at least fail to find a strong dependence of the logical probabilities of Omega's players' strategy on either their input (the agent's source) or the conditions in the expectation values it is evaluating (since the conditions are of the form
=X) which seems to be correlated with
)) only in the obvious way i.e. by determining the input to
).
Therefore, the highest expectation values will be computed for conditions of the form =DefectBot). Therefore the agent will defect.
I guess it wasn't mentioned explicitly in that discussion, but it's how I've come to think of the problem. Perhaps the most relevant part of that discussion is Eliezer's direct reply, here.
I see. However, your problem doesn't seem to be a realistic model of acausal bargaining with agents in other universes, since in such bargaining you know who you're cooperating with. For example, when an agent considers filling its universe with human utility, it does it in order to cooperate with a human FAI, not in order to cooperate with a paperclip maximizer (which would require a very different strategy namely filling its universe with paperclips).
It's more of a model for FAI meeting an alien AI in space. Suppose each side then has the choice of doing an arms buildup or not, and the payoffs for these choices are analogous to PD. (If one side builds up while the other doesn't, it can attack and conquer the other. If both sides build up, it's a stalemate and just wastes resources.) BTW, what was your "UDT anti-Newcomb problem" intended to be a model for?
I guess if both sides are using your decision theory, then whether the human FAI plays C or D against the alien AI depends on how much logical correlation the FAI thinks exists between its human designer and the alien AI's designer, which does make sense (assuming we solve the problem of the FAI just simulating its designer and already knowing what their output is).
It's more of a model for FAI meeting an alien AI in space.
Makes sense.
BTW, what was your "UDT anti-Newcomb problem" intended to be a model for?
Frankly, I didn't have a specific realistic scenario in mind. I came up with the anti-Newcomb problem as simple semi-artificial problem demonstrating the problems with quining in UDT. The reason I started thinking about these problems is that it doesn't seem "classical" UDT can be translated to realistic AGI architecture. UDT takes a finite number of bits and produces a finite number of bits whereas a realistic AGI has continuous input and output streams. Such an AGI has to somehow take into account a formal specification of its own hardware, and the natural way of introducing such a specification seems to me to go through introducing a precursor, specifically a precursor which is a Solomonoff average over all "theories of physics" containing the formal specification.
Consider the following decision problem which I call the "UDT anti-Newcomb problem". Omega is putting money into boxes by the usual algorithm, with one exception. It isn't simulating the player at all. Instead, it simulates what would a UDT agent do in the player's place.
This was one of my problematic problems for TDT. I also discussed some Sneaky Strategies which could allow TDT, UDT or similar agents to beat the problem.
This is an interesting approach. The way I'm currently thinking of this is that you ask what agent a UDT would design, and then do what that agent does, and vary what type an agent is between the different designs. Is this correct?
Consider the anti-Newcomb problem with Omega's simulation involving equation (2)
So is this equation (2) with P replaced with something else?
However, the computing power allocated for evaluation the logical expectation value in (2) might be sufficient to suspect P's output might be an agent reasoning based on (2).
I don't understand this sentence.
Hi jessicat, thx for commenting!
The way I'm currently thinking of this is that you ask what agent a UDT would design, and then do what that agent does, and vary what type an agent is between the different designs. Is this correct?
Sounds about right.
So is this equation (2) with P replaced with something else?
No, it's the same P. When I say "Omega's simulation doesn't involve P" I mean Omega is not executing P and using the result. Omega is using equation (2) directly, but P still enters into equation (2).
I don't understand this sentence.
Logical uncertainty (the way I see it), is a way to use a certain amount of computing resources to assign probabilities to the outcomes of a computation requiring a larger amount of computing resource. These probabilities depend on the specific resource bound. However, this is not essential to the point I'm making. The point I'm making is that if the logical uncertainty ensemble assigns non-zero probability to P producing XDT, we end up with logical correlation that is better avoided.
By the way, there are other reasons that we use quining to study decision theories within (virtual) mathematical universes. Most importantly, it lets us play with the logic of provability in a straightforward way, which gives us some really nice polynomial-time tools for analyzing the outcomes. See Benja's modal UDT implementation in Haskell and my intro to why this works (especially Sections 6 and 7).
Of course, there are things outside that scope we want to study, but for the moment provability logic is a good lamppost under which we can search for keys.
When one is programming an AI, it doesn't seem optimal for the AI to locate itself in the universe based solely on its own source code. After all, you build the AI, you know where it is (e.g. running inside a robot), why should you allow the AI to consider itself to be something else, just because this something else happens to have the same source code
IIUC, the point of making the agent use quining to locate itself in the world is that it allows it to cooperate with copies of itself in games such as program-equilibrium prisoner dilemma.
Your proposal based on origin will fail to cooperate in such cases.
(more realistically, happens to have a source code correlated in the sense of logical uncertainty)?
I'm not sure I understand what you are referring to. Quining allows the agent to shortcut Gödelian logical uncertainty in certain cases: the agent can not predict its own actions before it executes them, but if it notices that certain parts of the world contain copies of itself, it can infer that, whatever function they compute, it is the same function as its own. In various cases this is sufficient to achieve coordination.
IIUC, the point of making the agent use quining to locate itself in the world is that it allows it to cooperate with copies of itself in games such as program-equilibrium prisoner dilemma. Your proposal based on origin will fail to cooperate in such cases.
Not really. Two XDT agents with symmetric precursors will cooperate since conditioning on the output of one precursor will determine the output of the other precursor. An agent running equation (4') will cooperate with a regular UDT agent e.g. by letting pi be a UDT agent. In fact, this latter property doesn't seem to generalize to the other variants which looks like a good argument in favor of (4')!
Quining allows the agent to shortcut Gödelian logical uncertainty in certain cases: the agent can not predict its own actions before it executes them, but if it notices that certain parts of the world contain copies of itself, it can infer that, whatever function they compute, it is the same function as its own. In various cases this is sufficient to achieve coordination.
The problem is that from the precursor's point of view, such behavior is not always rational. More precisely, it is rational when there is a logical relation between the precursor's decision and the other copy (e.g. Omega copied the successor after its creation or Omega copied the precursor and used it to create a copy of the successor). It is not rational when the other copy occurs by coincidence. Indeed, a precursor running UDT will not choose to build a UDT agent in such situations.
Outline: I describe a flaw in UDT that has to do with the way the agent defines itself (locates itself in the universe). This flaw manifests in failure to solve a certain class of decision problems. I suggest several related decision theories that solve the problem, some of which avoid quining thus being suitable for agents that cannot access their own source code.
EDIT: The decision problem I call here the "anti-Newcomb problem" already appeared here. Some previous solution proposals are here. A different but related problem appeared here.
Updateless decision theory, the way it is usually defined, postulates that the agent has to use quining in order to formalize its identity, i.e. determine which portions of the universe are considered to be affected by its decisions. This leaves the question of which decision theory should agents that don't have access to their source code use (as humans intuitively appear to be). I am pretty sure this question has already been posed somewhere on LessWrong but I can't find the reference: help? It also turns out that there is a class of decision problems for which this formalization of identity fails to produce the winning answer.
When one is programming an AI, it doesn't seem optimal for the AI to locate itself in the universe based solely on its own source code. After all, you build the AI, you know where it is (e.g. running inside a robot), why should you allow the AI to consider itself to be something else, just because this something else happens to have the same source code (more realistically, happens to have a source code correlated in the sense of logical uncertainty)?
Consider the following decision problem which I call the "UDT anti-Newcomb problem". Omega is putting money into boxes by the usual algorithm, with one exception. It isn't simulating the player at all. Instead, it simulates what would a UDT agent do in the player's place. Thus, a UDT agent would consider the problem to be identical to the usual Newcomb problem and one-box, receiving $1,000,000. On the other hand, a CDT agent (say) would two-box and receive $1,000,1000 (!) Moreover, this problem reveals UDT is not reflectively consistent. A UDT agent facing this problem would choose to self-modify given the choice. This is not an argument in favor of CDT. But it is a sign something is wrong with UDT, the way it's usually done.
The essence of the problem is that a UDT agent is using too little information to define its identity: its source code. Instead, it should use information about its origin. Indeed, if the origin is an AI programmer or a version of the agent before the latest self-modification, it appears rational for the precursor agent to code the origin into the successor agent. In fact, if we consider the anti-Newcomb problem with Omega's simulation using the correct decision theory XDT (whatever it is), we expect an XDT agent to two-box and leave with $1000. This might seem surprising, but consider the problem from the precursor's point of view. The precursor knows Omega is filling the boxes based on XDT, whatever the decision theory of the successor is going to be. If the precursor knows XDT two-boxes, there is no reason to construct a successor that one-boxes. So constructing an XDT successor might be perfectly rational! Moreover, a UDT agent playing the XDT anti-Newcomb problem will also two-box (correctly).
To formalize the idea, consider a program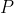
called the precursor which outputs a new program 
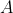called the successor. In addition, we have a program 
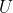called the universe which outputs a number )
called utility.
Usual UDT suggests for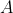
the following algorithm:
(1):=(\underset{f:I \rightarrow O}{\arg\max} \: E[U()|\forall j \in I: A(j)=f(j)])(i))
Here,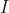
is the input space, 
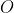is the output space and the expectation value is over logical uncertainty. 
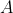appears inside its own definition via quining.
The simplest way to tweak equation (1) in order to take the precursor into account is
(2):=(\underset{f:I \rightarrow O}{\arg\max} \: E[U()|\forall j \in I: P()(j)=f(j)])(i))
This seems nice since quining is avoided altogether. However, this is unsatisfactory. Consider the anti-Newcomb problem with Omega's simulation involving equation (2). Suppose the successor uses equation (2) as well. On the surface, if Omega's simulation doesn't involve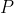
1, the agent will two-box and get $1000 as it should. However, the computing power allocated for evaluation the logical expectation value in (2) might be sufficient to suspect 
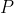's output might be an agent reasoning based on (2). This creates a logical correlation between the successor's choice and the result of Omega's simulation. For certain choices of parameters, this logical correlation leads to one-boxing.
The simplest way to solve the problem is letting the successor imagine that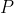
produces a lookup table. Consider the following equation:
(3):=(\underset{f:I \rightarrow O}{\arg\max} \: E[U()|P()=LUT(f))(i))
Here,)
is a program which computes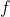 
using a lookup table: all of the values are hardcoded.
For large input spaces, lookup tables are of astronomical size and either maximizing over them or imagining them to run on the agent's hardware doesn't make sense. This is a problem with the original equation (1) as well. One way out is replacing the arbitrary functions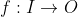
with programs computing such functions. Thus, (3) is replaced by
(4):=(\underset{\pi}{\arg\max} \: E[U()|P()=\pi)(i))
Where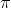
is understood to range over programs receiving input in 
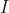and producing output in 
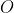. However, (4) looks like it can go into an infinite loop since what if the optimal 
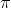is described by equation (4) itself? To avoid this, we can introduce an explicit time limit 
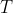on the computation. The successor will then spend some portion 
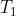of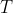 
performing the following maximization:
(4'):=(\underset{\pi}{\arg\max} \: E[U()|P()=S_{T_1}(\pi))(i))
Here,)
is a program that does nothing for time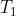 
and runs 
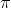for the remaining time 
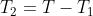. Thus, the successor invests 
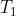time in maximization and 
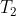in evaluating the resulting policy 
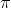on the input it received.
In practical terms, (4') seems inefficient since it completely ignores the actual input for a period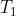
of the computation. This problem exists in original UDT as well. A naive way to avoid it is giving up on optimizing the entire input-output mapping and focus on the input which was actually received. This allows the following non-quining decision theory:
(5):=\underset{o \in O}{\arg\max} \: E[U()|P() \in F_{i,o}])
Here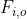
is the set of programs which begin with a conditional statement that produces output 
and terminate execution if received input was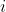 
. Of course, ignoring counterfactual inputs means failing a large class of decision problems. A possible win-win solution is reintroducing quining2:
(6):=\underset{o \in O}{\arg\max} \: E[U()|P()=\hat{F}_{i,o}(A)])
Here,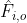
is an operator which appends a conditional as above to the beginning of a program. Superficially, we still only consider a single input-output pair. However, instances of the successor receiving different inputs now take each other into account (as existing in "counterfactual" universes). It is often claimed that the use of logical uncertainty in UDT allows for agents in different universes to reach a Pareto optimal outcome using acausal trade. If this is the case, then agents which have the same utility function should cooperate acausally with ease. Of course, this argument should also make the use of full input-output mappings redundant in usual UDT.
In case the precursor is an actual AI programmer (rather than another AI), it is unrealistic for her to code a formal model of herself into the AI. In a followup post, I'm planning to explain how to do without it (namely, how to define a generic precursor using a combination of Solomonoff induction and a formal specification of the AI's hardware).
1 If Omega's simulation involves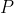
, this becomes the usual Newcomb problem and one-boxing is the correct strategy.
2 Sorry agents which can't access their own source code. You will have to make do with one of (3), (4') or (5).