Thanks for this, I found it helpful!
If you are still interested in reading and thinking more about this topic, I would love to hear your thoughts on the papers below, in particular the "multi-prize LTH" one which seems to contradict some of the claims you made above. Also, I'd love to hear whether LTH-ish hypotheses apply to RNN's and more generally the sort of neural networks used to make, say, AlphaStar.
https://arxiv.org/abs/2103.09377
"In this paper, we propose (and prove) a stronger Multi-Prize Lottery Ticket Hypothesis:
A sufficiently over-parameterized neural network with random weights contains several subnetworks (winning tickets) that (a) have comparable accuracy to a dense target network with learned weights (prize 1), (b) do not require any further training to achieve prize 1 (prize 2), and (c) is robust to extreme forms of quantization (i.e., binary weights and/or activation) (prize 3)."
https://arxiv.org/abs/2006.12156
"An even stronger conjecture has been proven recently: Every sufficiently overparameterized network contains a subnetwork that, at random initialization, but without training, achieves comparable accuracy to the trained large network."
https://arxiv.org/abs/2006.07990
The strong {\it lottery ticket hypothesis} (LTH) postulates that one can approximate any target neural network by only pruning the weights of a sufficiently over-parameterized random network. A recent work by Malach et al. \cite{MalachEtAl20} establishes the first theoretical analysis for the strong LTH: one can provably approximate a neural network of width d and depth l, by pruning a random one that is a factor O(d4l2) wider and twice as deep. This polynomial over-parameterization requirement is at odds with recent experimental research that achieves good approximation with networks that are a small factor wider than the target. In this work, we close the gap and offer an exponential improvement to the over-parameterization requirement for the existence of lottery tickets. We show that any target network of width d and depth l can be approximated by pruning a random network that is a factor O(log(dl)) wider and twice as deep.
https://arxiv.org/abs/2103.16547
"Based on these results, we articulate the Elastic Lottery Ticket Hypothesis (E-LTH): by mindfully replicating (or dropping) and re-ordering layers for one network, its corresponding winning ticket could be stretched (or squeezed) into a subnetwork for another deeper (or shallower) network from the same family, whose performance is nearly as competitive as the latter's winning ticket directly found by IMP."
EDIT: Some more from my stash:
https://arxiv.org/abs/2010.11354
Sparse neural networks have generated substantial interest recently because they can be more efficient in learning and inference, without any significant drop in performance. The "lottery ticket hypothesis" has showed the existence of such sparse subnetworks at initialization. Given a fully-connected initialized architecture, our aim is to find such "winning ticket" networks, without any training data. We first show the advantages of forming input-output paths, over pruning individual connections, to avoid bottlenecks in gradient propagation. Then, we show that Paths with Higher Edge-Weights (PHEW) at initialization have higher loss gradient magnitude, resulting in more efficient training. Selecting such paths can be performed without any data.
http://proceedings.mlr.press/v119/frankle20a.html
We study whether a neural network optimizes to the same, linearly connected minimum under different samples of SGD noise (e.g., random data order and augmentation). We find that standard vision models become stable to SGD noise in this way early in training. From then on, the outcome of optimization is determined to a linearly connected region. We use this technique to study iterative magnitude pruning (IMP), the procedure used by work on the lottery ticket hypothesis to identify subnetworks that could have trained in isolation to full accuracy. We find that these subnetworks only reach full accuracy when they are stable to SGD noise, which either occurs at initialization for small-scale settings (MNIST) or early in training for large-scale settings (ResNet-50 and Inception-v3 on ImageNet).
https://mathai-iclr.github.io/papers/papers/MATHAI_29_paper.pdf “In some situations we show that neural networks learn through a process of “grokking” a pattern in the data, improving generalization performance from random chance level to perfect generalization, and that this improvement in generalization can happen well past the point of overfitting.”
I don’t yet understand this proposal. In what way do we decompose this parameter tangent space into "lottery tickets"? Are the lottery tickets the cross product of subnetworks and points in the parameter tangent space? The subnetworks alone? If the latter then how does this differ from the original lottery ticket hypothesis?
The tangent space version is meant to be a fairly large departure from the original LTH; subnetworks are no longer particularly relevant at all.
We can imagine a space of generalized-lottery-ticket-hypotheses, in which the common theme is that we have some space of models chosen at initialization (the "tickets"), and SGD mostly "chooses a winning ticket" - i.e. upweights one of those models and downweights others, as opposed to constructing a model incrementally. The key idea is that it's a selection process rather than a construction process - in particular, that's the property mainly relevant to inner alignment concerns.
This space of generalized-LTH models would include, for instance, Solomonoff induction: the space of "tickets" is the space of programs; SI upweights programs which perfectly predict the data and downweights the rest. Inner agency problems are then particularly tricky because deceptive optimizers are "there from the start". It's not like e.g. biological evolution, where it took a long time for anything very agenty to be built up.
In the tangent space version of the hypothesis, the "tickets" are exactly the models within the tangent space of the full NN model at initialization: each value of yields a corresponding function-of-the-NN-inputs (via linear approximation w.r.t. ), and each such function is a "ticket".
I am interested in making this understood by more people, so please let me know if some part of it does not make sense to you.
I confess I don't really understand what a tangent space is, even after reading the wiki article on the subject. It sounds like it's something like this: Take a particular neural network. Consider the "space" of possible neural networks that are extremely similar to it, i.e. they have all the same parameters but the weights are slightly different, for some definition of "slightly." That's the tangent space. Is this correct? What am I missing?
Picture a linear approximation, like this:
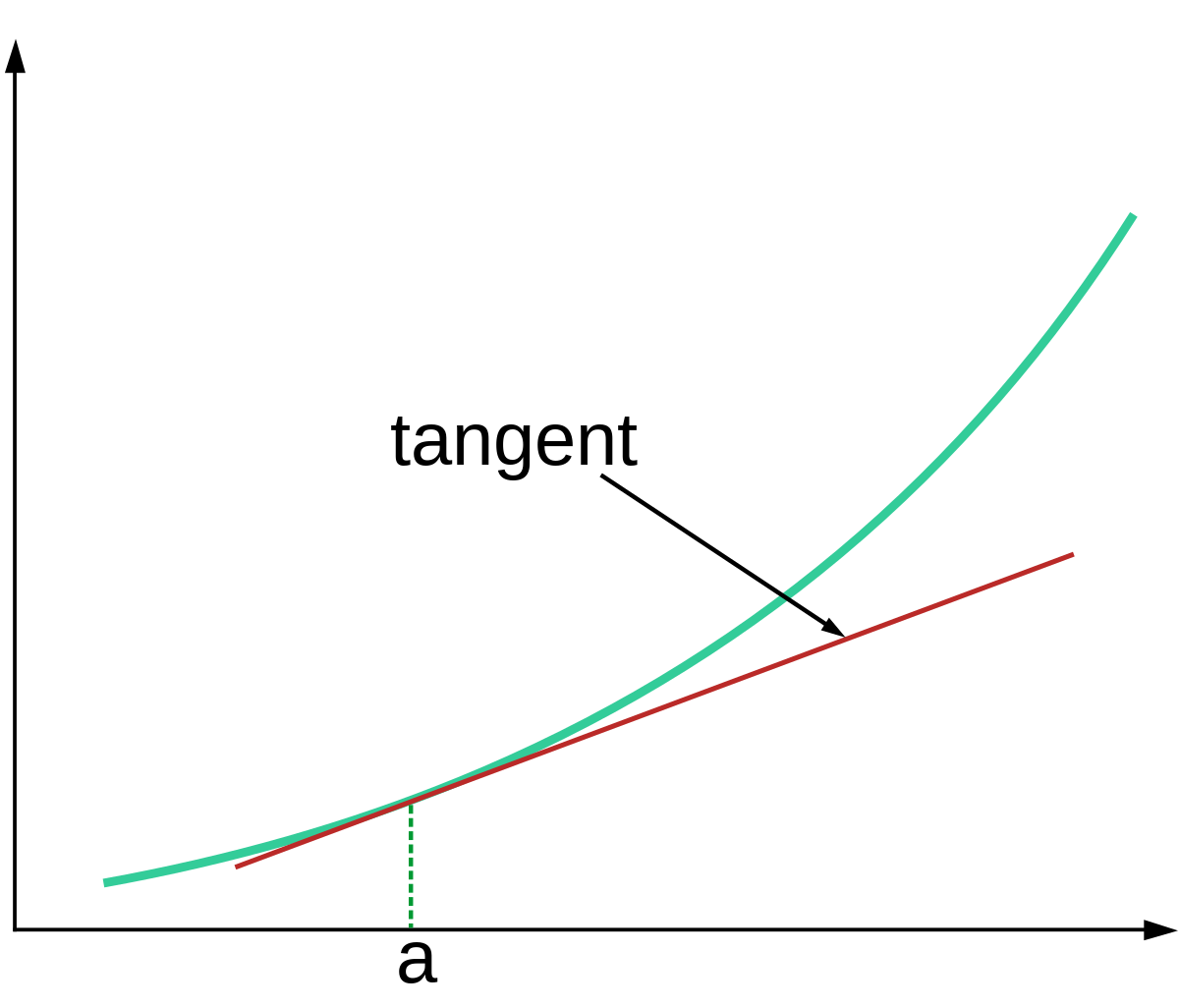
The tangent space at point is that whole line labelled "tangent".
The main difference between the tangent space and the space of neural-networks-for-which-the-weights-are-very-close is that the tangent space extrapolates the linear approximation indefinitely; it's not just limited to the region near the original point. (In practice, though, that difference does not actually matter much, at least for the problem at hand - we do stay close to the original point.)
The reason we want to talk about "the tangent space" is that it lets us precisely state things like e.g. Newton's method in terms of search: Newton's method finds a point at which f(x) is approximately 0 by finding a point where the tangent space hits zero (i.e. where the line in the picture above hits the x-axis). So, the tangent space effectively specifies the "search objective" or "optimization objective" for one step of Newton's method.
In the NTK/GP model, neural net training is functionally-identical to one step of Newton's method (though it's Newton's method in many dimensions, rather than one dimension).
Nice article. It was easy to read, the explanations were mostly clear. I've finally learned what LTH is, yay. I have a few questions.
-
What is a subnetwork of a convolutional neural network? Is it the function obtained by zeroing some non-bias parameters? Does the same also hold for resnets, i.e. all skip connections remain?
-
Can you add a qualification in the very beginning saying that all this applies to multilayer perceptrons and CNNs in supervised learning rather than all NNs?
-
You often use the word dense, and sometimes I don't understand if you mean a fully connected layer or an unpruned (fully connected or convolutional) layer. Can you clarify it for all occurrences where it might be unclear?
In some follow-up work, Frankle and Carbin also found it necessary to use "late resetting", which means resetting the weights of the subnetwork not to their original values from initialization but to their values from 1% - 7% of the way through training the dense network.
Do you mean weight that the network had after 1%-7% of all iterations have happened? Or do you mean moving 1%-7% of the line segment from the initial weights to the weights when the training was stopped?
- In the case of convolutional neural networks, the subnetwork can vary depending on how you choose the pruning granularity. In the LTH, they apply an unstructured pruning, i.e. they replace individual weights in the convolution filters by a 0 value. But you could imagine applying a structured pruning, replacing vectors, kernels or even complete filters by zeroes. The architecture of the subnetwork is thus not necessarily different, but the information that flows in the network will be as your network is now sparse. So, you generally don't want to change the overall architecture of the network, keeping skip connections intact for example.
- Although the LTH was empirically discovered on MLP and CNNs on supervised learning, I see more and more occurrences of LTH on other training paradigms, e.g. this one in the RL context
- AFAICT, when the word "dense" was used here, it was always in opposition to "sparse".
Concerning the "late resetting", your first intuition was correct, instead of resetting the weights to their value at iteration 0 (the initialization), they reset them to their value at a later iteration (after 1%-7% of the total number of iterations). They've actually done another paper studying what happens in early training and why the "late resetting" might make sense.
Hope that helps !
Financial status: This is independent research. I welcome financial support to make further posts like this possible.
Epistemic status: The thread of research I’m reviewing here has been contentious in the past so I expect to make updates based on the comments.
Outline
This is my attempt to understand the lottery ticket hypothesis.
I review the original paper, as well as two follow-up papers and one related paper.
I also go over four previous lesswrong posts on this subject.
Introduction
The lottery ticket hypothesis is a hypothesis about how neural network training works. It was proposed in 2018 by Jonathan Frankle, a PhD student at MIT, and Michael Carbin, a professor at MIT. It suggests that, in a certain sense, much of the action in neural network training is during initialization, not during optimization.
Research that sheds light on neural network training is relevant to alignment because neural network architectures may eventually become large enough to express dangerous patterns of cognition, and it seems unlikely that these patterns of cognition can be detected by input/output evaluations alone, so our only choices seem to be (1) abandon the contemporary machine learning paradigm and seek a new paradigm, or (2) augment the contemporary machine learning paradigm with some non-input/output method sufficient to avoid deploying dangerous patterns of cognition. Insights into contemporary machine learning effectiveness is relevant both to determining whether course (1) or (2) is more promising, and to executing course (2) if that turns out to be the better course.
The lottery ticket hypothesis
The lottery ticket hypothesis (or LTH), as originally articulated by Frankle and Carbin, says:
A "subnetwork" means that you take the original neural network and clamp some of the weights to zero, so a network with N weights has 2N subnetworks. The lottery ticket conjecture, which is an extension of the lottery ticket hypothesis but which Frankle and Carbin are careful to point out is not tested directly in their original paper says:
The lottery ticket conjecture is much more interesting from the perspective of understanding neural network training, and seems to be referred to as the "Lottery Ticket Hypothesis" both in the literature and on this site, so I will follow that convention in the remainder of this post. I will take the original lottery ticket hypothesis as an implication.
In neural network training, in the absence of the lottery ticket hypothesis, we think of the role of SGD as pushing the weights of the overall network towards a local minimum of a loss function, which measures the performance of the network on a training set:
On this view, the point in the loss landscape at which we begin optimizing — that is, the way we initialize the weights at the beginning of training — is not really where the main action is. Initialization might well be important, but the main point of initialization is to start in some not-completely-crazy part of the loss landscape, after which the optimization algorithm does the real work.
The lottery ticket hypothesis says that actually we should view a neural network as an ensemble of a huge number of sparse subnetworks, and that there is some as-yet poorly understood property of the initial weights of each of these subnetworks that determines to how quickly they will learn during training, and how well they will generalize at the end of training. The lottery ticket hypothesis says that among this huge ensemble of subnetworks, some number of subnetworks have this "trainability" property by virtue of having been initialized in accord with this as-yet poorly understood property. What the optimization algorithm is implicitly doing, then, is (1) identifying which subnetworks have this property, (2) training and upweighting them, and (3) downweighting the other networks that do not have this property.
Now this "lottery ticket view" of what is happening during neural network training does not exactly overturn the classical "whole network optimization view". The two views are of course compatible. But the lottery ticket hypothesis does make predictions, such as that it might be possible to give our entire network the as-yet poorly understood initialization property and improve training performance.
Now it’s not that the winning "lottery ticket" is already trained, it just has some property that causes it to be efficiently trainable. There is some follow-up work concerning untrained subnetworks, but I do not believe that it suggests that neural network training consists of simply picking a subnetwork that already solves the task at hand. I discuss that work below under "supermasks" and "weight-agnostic networks".
Also, if some network does contain a subnetwork that would perform well at a task on its own, that does not mean that there is a neuron within the network that expresses the output of this particular subnetwork. The output of any one neuron will be a combination of the outputs of all the subnetworks that do not mask that neuron out, which will generally include exponentially many subnetworks.
So how did Frankle and Carbin actually investigate this? They used the following procedure:
Train a dense neural network on a computer vision task
After training, pick a subnetwork that discards the bottom X% of weights ranked by absolute magnitude, for some values of X from 5% to 95%
Now reset the remaining weights to the value they had when the original dense network was initialized
Train this reduced subnetwork on the same computer vision task
Compare this to training the same reduced subnetwork initialized with freshly randomized weights
It turns out that the subnetworks produced by step 4 train faster and ultimately generalize better than the subnetworks produced by step 5. On this basis the authors conjecture that there was some special property of the initialization of this particular subnetwork, and that due to this property it trained efficiently relative to its peers, and that it was thus implicitly upweighted by the optimization algorithm.
In many of the experiments in the paper, the authors actually iterate steps 2-4 several times, pruning the weights gradually over several re-training phases rather than all at once after training the dense network just once.
When running experiments with larger architectures (VGG-19 and ResNet), the authors find:
In some follow-up work, Frankle and Carbin also found it necessary to use "late resetting", which means resetting the weights of the subnetwork not to their original values from initialization but to their values from 1% - 7% of the way through training the dense network.
Deconstructing lottery tickets: signs, zeros, and the supermask
The suggestion that there might be some property of the initialization of a neural network that causes it to learn quickly and generalize well has prompted follow-up work trying to uncover the exact nature of that property. Zhou et al from Uber AI investigated the lottery ticket hypothesis and found the following.
First, among the weights that the sparse subnetwork is reset to in step 3, only the sign matters. If you replace all the positive weights with 1 and all the negative weights with -1 then the subnetwork still trains efficiently and generalizes well, but if you randomize all the weights then this property disappears.
Second, if instead of clamping the pruned weights to zero you clamp them to their initial value from the dense network, then the good performance disappears. They hypothesize that clamping small-magnitude weights to zero is actually acting as a form of training since perhaps those weights were heading towards zero anyway.
Thirdly, and most fascinatingly, that they can find some "supermasks" such that merely applying the mask to an untrained dense network already produces better-than-random results. It is not that the supermask identifies a subnetwork that already solves the task. The untrained subnetwork identified by a supermask actually performs very poorly by the standards of any trained supervised learning system: 20% error on MNIST compared to 12% achieved by linear classification and 0.18% achieved by trained convnets. But 20% error is much better than the 90% error you would expect from chance predictions[1]. The authors suggest that we think of masking as a form of training.
One ticket to win them all: generalizing lottery ticket initializations across datasets and optimizers
In this paper, Morcos et al show that a "winning lottery ticket" subnetwork found by training a dense network on one dataset with one optimization algorithm still retains its attractive properties of efficient training and good generalization when the subnetwork is later trained on a different dataset or optimized by a different optimizer.
Weight-agnostic neural networks
This paper from Google Brain finds neural network architectures that perform well no matter which weights are inserted into them. They demonstrate networks solving reinforcement learning problems when all of their weights are set to 1, and then still solving the same problem when all of their weights are set to 2, 10, etc. The paper uses a completely different method to find architectures from the one used by Frankle and Carbin so this paper is a bit outside the lottery ticket literature, but it provides further evidence that weight training may not be the entirety of "where the action is at" in neural network training.
Daniel on the lottery ticket hypothesis and scaling
Daniel Kokotajlo asks whether the lottery ticket hypothesis, if true, would suggest that machine learning will continue to solve more problems as we apply more computing power to it. The reason is that more computing power means we can train networks with more parameters, which means we are searching over more "lottery tickets", which might mean we are able to solve increasingly difficult problems where lottery tickets are harder and harder to come by.
Evan on the lottery ticket hypothesis and deep double descent
Evan Hubinger speculates about whether the lottery ticket hypothesis might explain the deep double descent phenomenon:
John on the lottery ticket hypothesis and parameter tangent spaces
John Swentworth proposes an update to the lottery ticket hypothesis informed by recent results that show that the weights of large neural networks actually don’t change very much over the course of training on practical machine learning problems:
I don’t yet understand this proposal. In what way do we decompose this parameter tangent space into "lottery tickets"? Are the lottery tickets the cross product of subnetworks and points in the parameter tangent space? The subnetworks alone? If the latter then how does this differ from the original lottery ticket hypothesis?
John quotes the following synopsis of the lottery ticket hypothesis:
The "supermask" results above do suggest that this synopsis is accurate, so far as I can tell, but it’s important to realize that "decent" might mean "better than random but worse than linear regression", and the already-present subnetwork does not just get reinforced during training, it also gets trained to a very significant extent. There is a thread between Daniel Kokotajlo and Daniel Filan about this synopsis that references several papers I haven’t reviewed yet. They seem to agree that this synopsis is at least not implied by the experiments in the original lottery ticket hypothesis paper, which I agree is true.
Abram on the lottery ticket hypothesis and deception
Abram points out that the lottery ticket hypothesis being true could be disheartening news from the perspective of safety:
Daniel provides the following helpful summary of Abram’s argument in a comment:
I previously attempted to summarize this post by Abram.
Conclusion
It’s exciting to see these insights being developed within the mainstream machine learning literature. It’s also exciting to see their safety implications beginning to be fleshed out here. I hope this post helps by summarizing some of the experimental results that have led to these hypotheses.
We would expect 90% error from chance predictions since MNIST is a handwritten digit recognition dataset with 10 possible labels. ↩︎