We depend on our words... Our task is to communicate experience and ideas to others... The word "reality" is also a word, a word which we must learn to use correctly.
— Niels Bohr, Philosophy of Science Vol. 37 (1934), p. 157
While trying to write about some of the new things that have been bothering me, I kept coming back to this old one, since it seems so fundamentally important. Anything else I might say would have to refer to it, so I decided to write it up in a way that I can point to it with a link, the way that other topics on this site are so efficiently dealt with.
The point of this essay is that there is more than one reality. I mean that in as un-mystical a way as possible. I mean that the words "real" and "exist" are so oversubscribed that it would be better if there were several words, one for each concept. I see this come up repeatedly in arguments as people talk past each other, with one person saying that X exists, but meaning "X exists," while another says that X does not exist, because "X does not exist." There's usually also a pejorative association with putting something in a not-real box, to say that X is irrelevant because it does not exist (but it might exist!).
I can't write down a complete list of all these reality-boxes because although there are a few well-defined, distinct meanings, there are also some hazy, overlapping categories. In this essay, I'll talk about five, which seem to be the clearest ones.
- physical reality
- mathematical reality
- narratives/reasons-why, with causality being the most precise "reason-why"
- conventional: things that are real (really real!) only because people say they are
- subjective: the direct experience of being a mind, which is in a different reality-box from the objective study of physical brains.
This is not a complete list because some (particularly "narrative reality," number 3) could be subdivided, and other things that could be called real are completely missing, such as value judgements. (It depends on whether you think "good" and "bad" are objective. I'm on the fence about that right now.)
For the purposes of this essay, I'll stick to the five above.
Reality 1: physical
The first thing most of us think about when we hear the words "real" or "to exist" is physical reality, and we consider it valid to talk about the physical world as being real. (Idealists like Plato or George Berkeley would disagree, but that's a minority view.) In this sense, physical reality is the narrowest meaning that "real" can have.
The pencil that I'm holding exists, at least the swarm of atoms does: the stuff that makes up the pencil is real in a different sense from how I identify some stuff as belonging to the pencil and other stuff as the air around it. It's the material (or "thing in itself") that is physically real, whether that material is best described as atoms, nucleons, quarks, or something else.
The reason we (most of us) are convinced that physical reality exists is because it's so consistent. There's object permanence: I hide my pencil under a piece of paper, remove the paper, and it's still there. At a fundamental level, there are conservation laws, like conservation of charge and mass-plus-energy. (Even more fundamentally, the conservation laws can be derived from symmetries of space-time and the Standard Model. The fact that "stuff doesn't arbitrarily go away" runs deep.)
Despite this impression that physical reality is the most undeniable reality, it's also just out of reach. We can't directly experience the existence of material reality: instead, we have sense perceptions—sight, hearing, touch—that usually correlate well with it, but not always. The scientific method, which we use to formally demonstrate a thing's reality, is more like a list of "gotchas to look out for" than a surefire algorithm. It's hard, for instance, to decide How Experiments End, how to know that you have enough data for a satisfactory case and haven't missed any confounding effects. Also, we want to distinguish what really exists (a glob of stuff) from our models about what really exists (my pencil, atoms, nucleons, quarks...), but we can only directly know the models in our heads.
Reality 2: mathematical/logical
Another, completely different meaning of "to exist" is to say (for example) that the solution of
exists. It doesn't mean anything remotely like "my pencil exists." The problem and its solution, , are ideas, rather than stuff.
However, this idea is not an arbitrary idea. It's objective, as the physical world is objective, in the sense that any two beings from any cultures who understand the statement of the problem would come to the conclusion that the solution is correct. There is an undeniableness to the conclusion, just as there's an undeniableness to the conclusion that my pencil exists, but they're not undeniable in the same way. (And "undeniableness" can only be pushed so far: a particularly ornery person could just refuse to admit it. These two cases each have a high degree of undeniableness.)
Mathematical statements are more undeniable than physical ones. The method of proof, pioneered by Euclid, is now at a point where it can be mechanized. It may be hard for computers (and humans) to search for a proof, but if a mathematical statement is expressed as a sentence of symbols with a specified set of rewrite rules (the rules of logic), a computer can check every step of a proposed proof. In the above, consider applying the following rewrite rules, in order:
- Replace with .
- Replace with .
- Replace with .
- Replace with .
After the last step, the equation becomes , a tautology. (It could be put into a common form for all algebraic tautologies by dividing or subtracting both sides of the equation by 3.) Any machine that can effectively rewrite sentences in this way can check the proof, which makes it something external to the thinker, independent of human whims and opinions.
Western philosophers have been preoccupied with mechanized logic for centuries, and some (like Plato) have been so impressed by it that they were willing to consider math real and the physical world not-real. Consider, for instance, that mathematical objects have a stronger object permanence than physical ones: if I put my pencil under a piece of paper, it might not be there when I remove the paper. (Because I already believe in physical existence, I would puzzle over what could have dissolved it, or if there was some other trick to it—I would think the straightforward conclusion is wrong.) The equation , however, will always have one solution, and that solution will always be .
While it's true that physical existence is a very different thing from mathematical existence, I don't believe that we have to pick one as really real and the other as somehow subordinate to it. "Reality" is a word, and words are sometimes oversubscribed with multiple meanings. To say, "X is really real, Y isn't," acknowledges their differences but also plays favorites—it's an emotional statement of preference—the speaker cares about X and not Y.
The key thing that distinguishes these reality boxes is what method we use to determine if something is real or exists. For mathematics and logic, the method is a priori proof, and for physical objects and situations, the method is a posteriori experiment or observation. For an a priori proof, data from the external world is unnecessary and superfluous—you can do it in your head (or, at least, do each piece in your head, writing down partial results to remember them). An a posteriori experiment or observation strictly needs data from the external world. This distinction may seem obvious now, but it was the source of a lot of confusion before the scientific method, and before philosophers like Hume and Kant.
There are other things that we talk about as real or existing that don't fit into these categories. It felt like a breakthrough to me when I realized that there could be other categories, other reality-boxes in which claims can be deposited if true and not false, that are as significant and meaningful as physical and mathematical realities.
Reality 3: causality (and reasons-why in general)
The first time I realized I needed a new reality-box was to make sense of causality. I'm a physicist—I studied physics through a Ph.D. and worked on high-energy collider data for more than a decade—but I never understood what people meant when they talked about causality in physics. I didn't see anything in physics (in physical reality, that is!) that looks like causality.
One thing that I should clarify is that physicists do use the word "causality" a lot, but that's mostly in relativity, in which the word is used to mean "before/after relationship." Relativity downgrades the concept of before/after from a strict inequality—every space-time point in classical physics is either before or after a different one—into a partial inequality—every space-time point in relativistic physics is either before a different one, after it, or neither. The third case is reserved for space-time points that are separated by too large a distance/too short a time for information to pass from one to the other at the speed of light. Space-time points with this "space-like separation" have a time ordering that depends on your perspective (frame of reference).
Although before/after has some bearing on causality, in that can't cause unless is before , there's more to causality than that. In common and in philosophical usage, " causes " means "if happens, then will happen." and have to be properties that can be true or false, not just positions in space-time. There are probabilistic versions of causality in which only makes more likely to happen, but that's not the crux of the issue here.
The issue, as I saw it, is that the physics of a closed system, even a classical system, doesn't have these if-then relationships. Suppose you have a classical billiards table and say, "If the white ball hits the 8-ball, then the 8-ball will go into the pocket." You can calculate angles and Newtonian forces for the situation in which the white ball misses and the situation in which the white ball hits the 8-ball, and conclude that only the white ball hitting the 8-ball results in it going into the pocket. But that presupposes two possible starting points: two different trajectories for the white ball. If the billiards table is the entire universe, as a theory of physics ought to be, then conditions at the beginning of time or a chain stretching back into the infinite past would completely determine the white ball's trajectory. There is no if-then because there is no "if."
Suppose we were to apply the same terminology to mathematical reality. Say that is "" and is "." It doesn't make any sense to say that "" causes "." For one thing, these two statements are symmetric: you could equally say that "" causes "," and one of the properties of causality is that it is asymmetric.
Adding quantum mechanics complicates the situation, but in the opposite way than people usually say it does. Quantum mechanics allows some properties to mix—a physical situation can be 30% and 70% not-, for instance (actually, the weights are complex numbers that square to probabilities). Some interpretations of quantum mechanics (e.g. Copenhagen) say that mixed states "collapse" to become non-mixed states, through a variety of mechanisms, while other interpretations of quantum mechanics say that the states are always mixed, but they either asymptotically limit to a mostly pure state (e.g. decoherence) or we only perceive pure states because our consciousness is part of the mixture (e.g. Hugh Everett's many-worlds). At least in the collapse theories, you can actually have an if-then: the white ball may be in a mixture of a trajectory toward the 8-ball and a trajectory that would miss the 8-ball, but then it collapses into only one trajectory. If that trajectory would hit the 8-ball, then the 8-ball would go into the pocket, otherwise not—we can talk about causality. In theories like many-worlds, there is no if-then: instead of a statement of causality, we have something more like a statement of geometry: in the parts of the multiverse where the white ball hits the 8-ball, those histories also include the 8-ball going into the pocket, and vice-versa.
People often say that classical physics is causal and quantum mechanics undermines causality. I have never understood that: it has always seemed that classical physics cannot be causal and only some interpretations of quantum mechanics allow for causality. (An open classical physics, like a game engine that allows players to change the course of the physics simulation through controller input, would be causal. However, most of us think that the physical world is closed; it doesn't have avatars—literally gods—at the console.)
The breakthrough for me was learning about Judea Pearl's interpretations of causality as a statement about possible worlds. These are not the many worlds of Hugh Everett's interpretation of quantum mechanics, in which all worlds are equally valid. In this interpretation of causality, one world is actual and the others are only consistent with physical laws (or whatever rules are driving the system). To say, "If the white ball hits the 8-ball, then the 8-ball will go into the pocket," is to say that all of the possible worlds in which the white ball hits the 8-ball, the 8-ball also goes into the pocket. Which one corresponds to the special, actual world is a different matter. The actual world is the one we use simple verb tenses for ("the 8-ball goes into the pocket") and the possible worlds are the ones we use subjunctive tenses for ("the 8-ball would go into the pocket"). I wrote a lot more about it here.
Pearl's interest in causality is pragmatic, and he assumes that an experimenter can change which world we're in without saying how—metaphysically—that happens. Free choice, the ability to set up some experiments in which is true and other experiments in which is false, is an essential part of deriving conclusions from experiments. (One of the ways to escape the conclusion of Bell's Inequality is to assume that the experimenters are forced by the same physics as what they're studying to choose to make some measurements and not others: superdeterminism.)
The way that I reconcile this with a closed physical universe is to say that these possible worlds and causality are not a part of the physical reality at all—they are a different reality, as different from the physical world as the physical world is from mathematics. Causality is an example of a thing that I could call reasons-why or narratives. While causality can be modeled precisely, reasons-why are more general, and narratives can be broad enough to include social contexts or mythologies. For now, let's focus on causality because we can be precise.
Causality is distinct from physical reality
Instead of just asserting it, I'll illustrate an example in which two different causal structures can be applied to the same physical reality: causality is not determined by the underlying physical reality. (It is a "further fact," i.e. causality does not "supervene" on physical reality because a difference in causality is not reflected by a difference in the physical reality.)
The example is a world in which a wave propagates in one dimension.
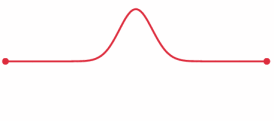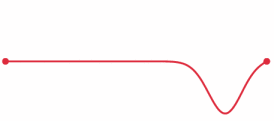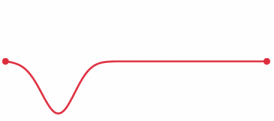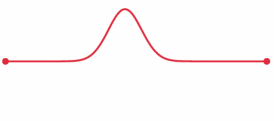
In this world, there's only one spatial dimension, one time dimension, and a field filling this space that can be excited, the "tension of the string." Above, you see the spatial dimension as a horizontal line, tension is represented vertically, and this example has two fixed endpoints that act to reflect the wave. Time is represented as time: it's an animated GIF.
We could also represent space horizontally and time vertically, in which case the wave would be a diagonal blob of heightened density that changes direction at the endpoints.
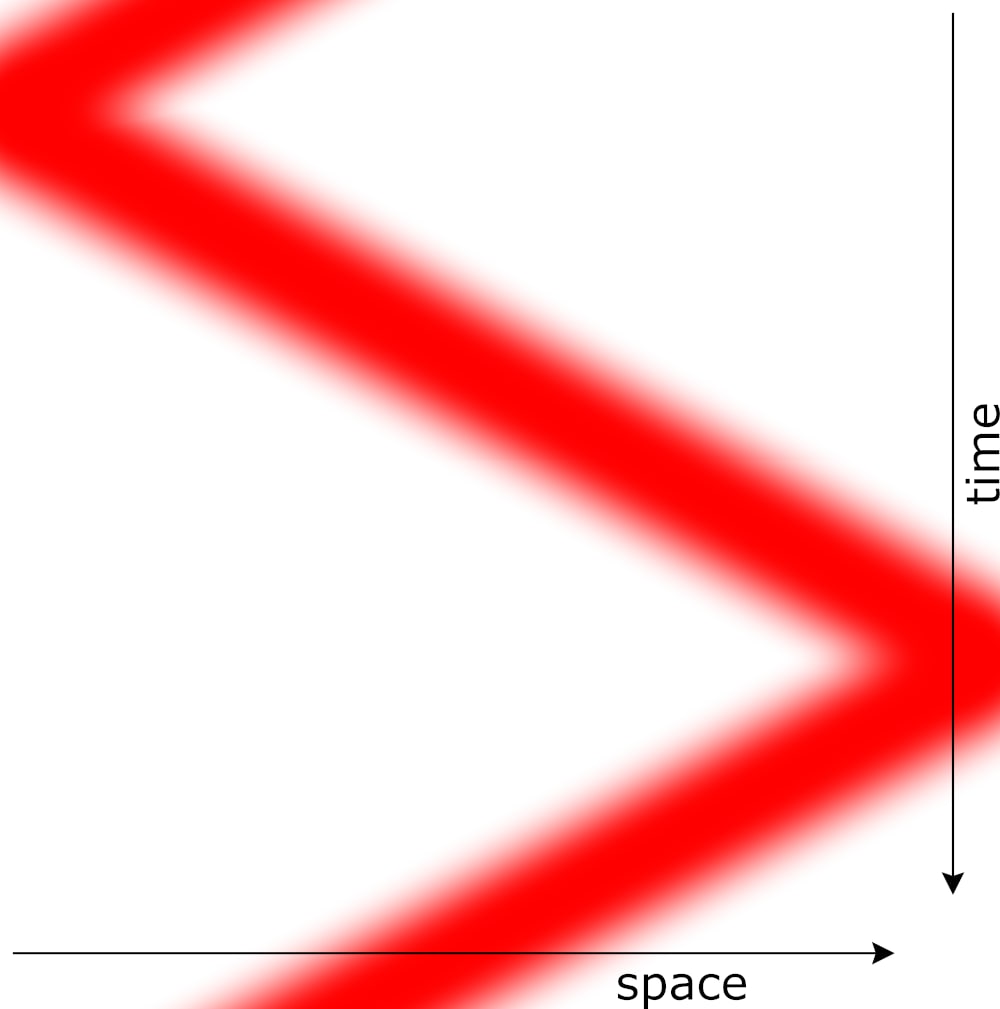
The equation this obeys is
where is the tension ("redness") at each point in space and time , and are second derivatives with respect to space and time, and is a constant that happens to be equal to the speed of the wave. (Derivatives are differences in the values of at nearby points in space and time . On a continuum, "nearby" points are infinitesimally separated. Second derivatives are differences in differences.)
If is given for some time-slice or is given for some space-slice (or similar), there is exactly one solution for every value of . There is no wiggle room, no possibility of considering other possible worlds: this is the only one.
Now I'm going to argue that the distribution and the relationship described by the wave equation belong to the physical reality (what "is"), while possible worlds, the freedom to perform experiments, and causal statements about it are parts of a different kind of reality, in a different reality-box from the physical (what "would be"). Here's an example of a causal statement: "If the crest of the wave at is at (the crest is the at which is maximized), then at future times , the crest of the wave moves to ."
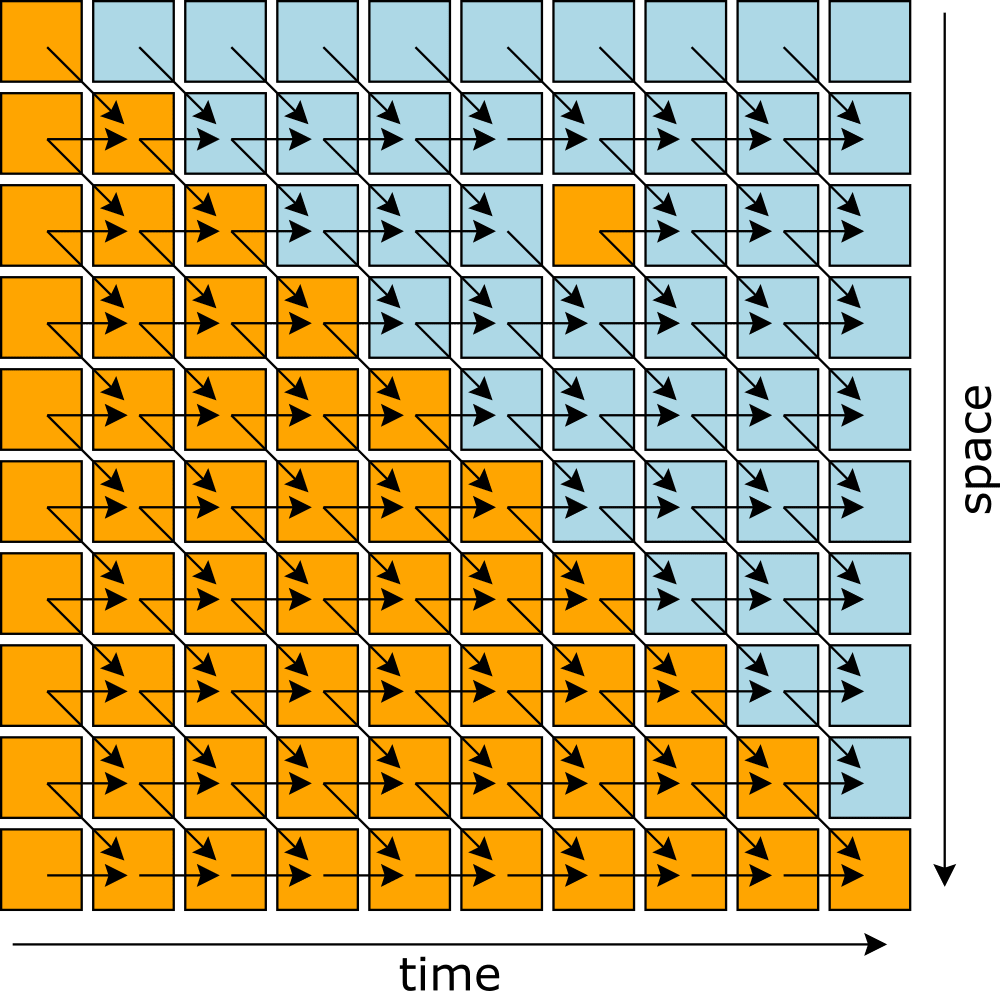
Before doing so, I'm going to simplify the physical situation so that it's easier to mentally calculate without giving up on the important properties. Replace the continuous space and time with a discrete grid (10×10), remove the reflection at the endpoints, and replace the continuous values of with booleans: false (blue) or true (orange). Now we don't have to think about infinitesimals or reflection.
Suppose we are presented with a physical reality like this:
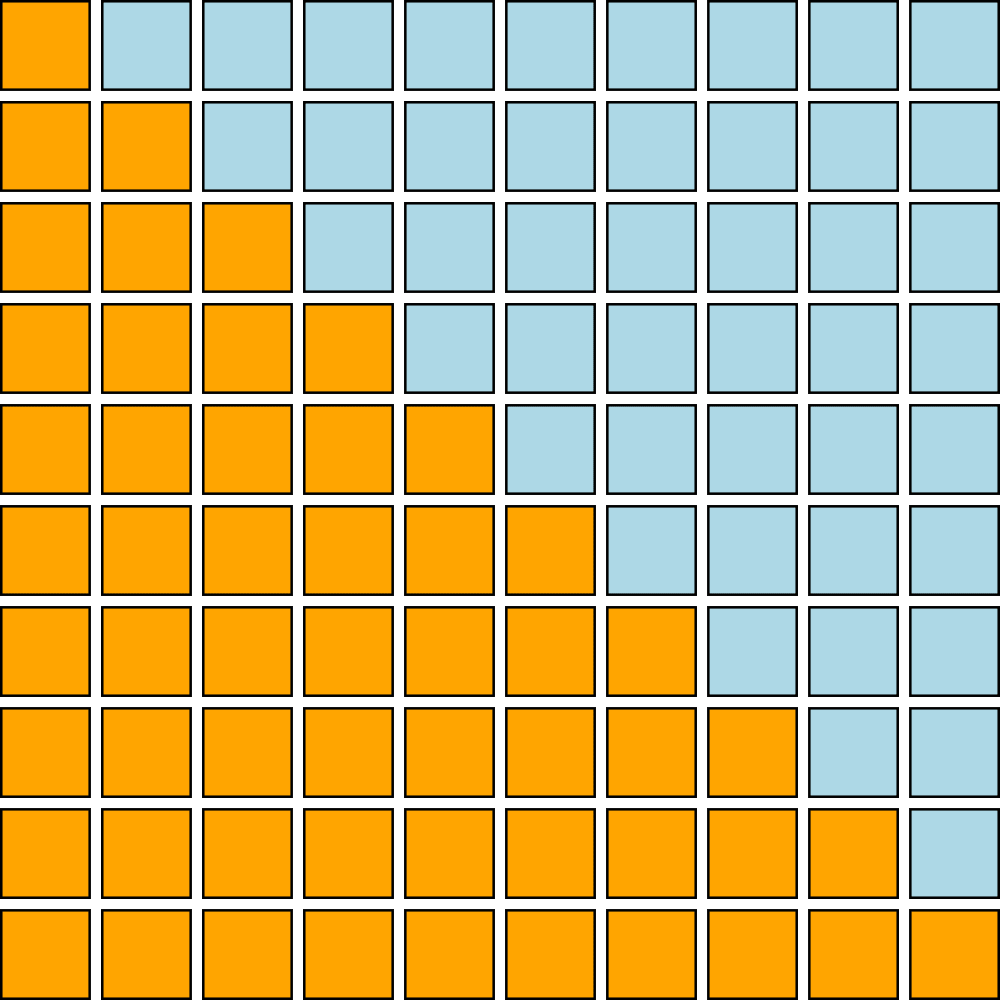
Of the possible patterns we could have been presented with, this one has some regularity and we'd be tempted to write down a rule for it. With rows labeled and columns , the rule could be
(each grid square is defined in terms of the one above it and to the left and the one directly above it). Alternatively, the rule could be
(each grid square is defined in terms of the one directly to the left and the one above it and to the left). There may be other rules that also describe this pattern. Let's call these rule and rule, respectively.
Either of these rules would completely describe the whole grid if initial and boundary conditions are given, such as
Whereas a wave equation is a descriptive relationship between grid points, rule and rule go further and describe an implementation strategy—which grid cells are to be computed from which other grid cells—and the two implementation strategies are different from each other.
Rule has the following dependencies: each depends on and . These dependencies form a directed acyclic graph, starting from the initial and boundary conditions, so it can be computed iteratively, each row after the previous row. The dependencies are illustrated as arrows below, and since the flow is row-by-row, we can call the rows the "time" dimension.
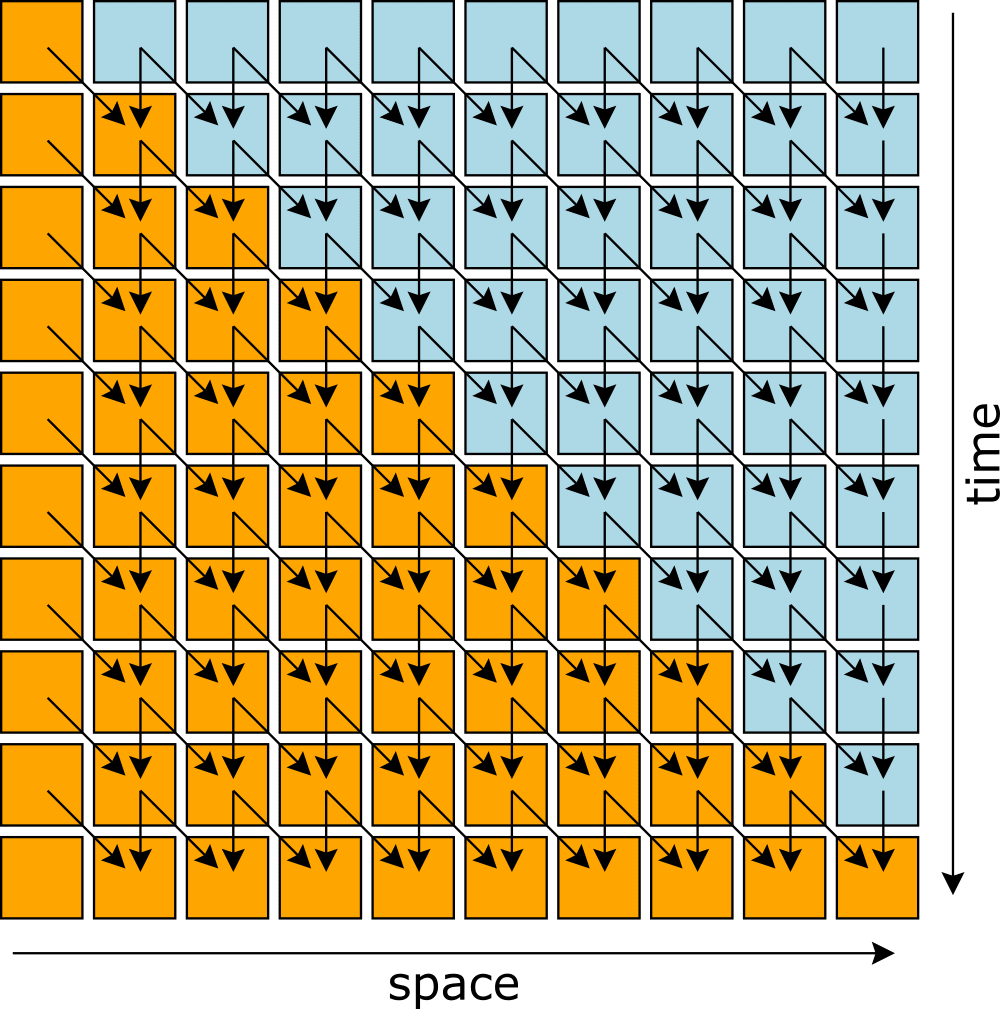
Rule has the following dependencies: each depends on and . These dependencies form a different directed acyclic graph, which can be computed iteratively, each column after the previous column. With these dependencies, we'd want to call the columns the "time" dimension.
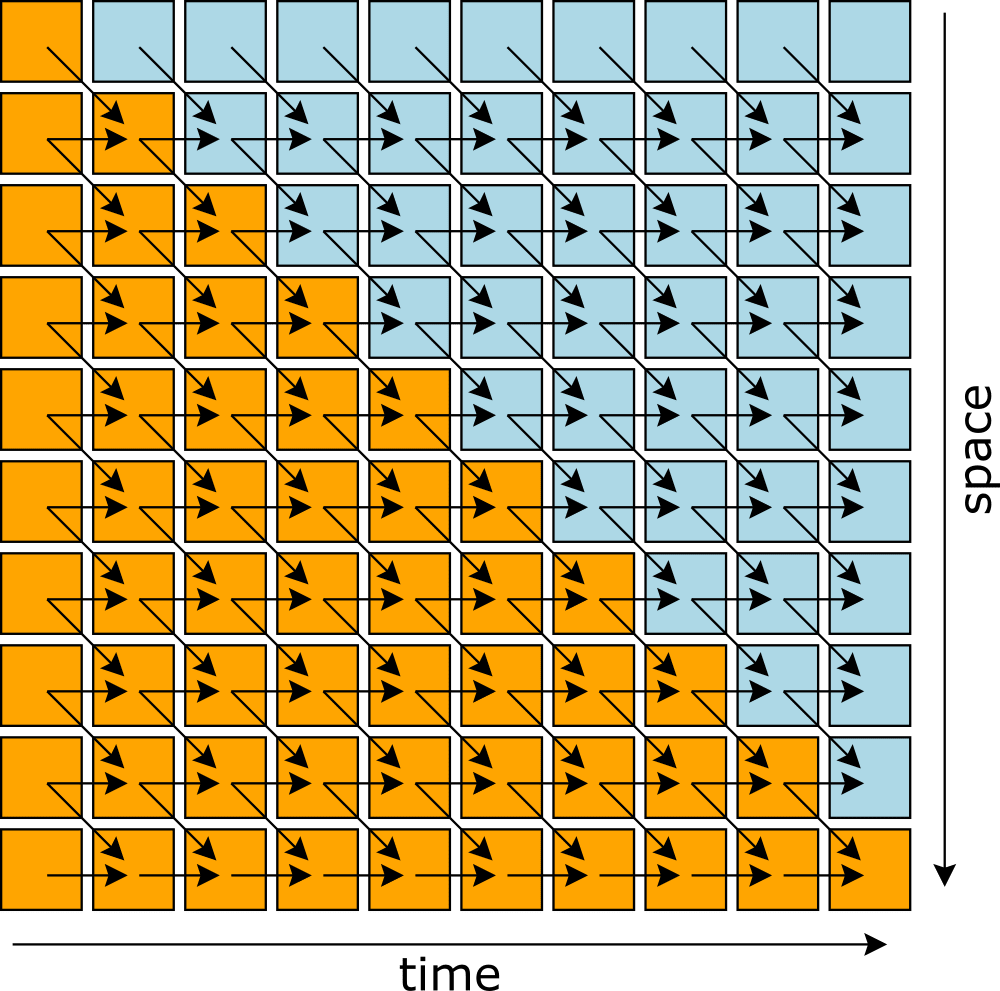
In both cases, the directed acyclic graph of the computation strategy is the same as the graph of causal relationships. We label "time" in such a way that causality's graph always points in the direction of later times. This relationship between causality and a computation graph is a neat result, since the before/after relationship in relativity is also directed and acyclic (a partial ordering).
Surely, though, we should be able to tell the difference between rule and rule, right? They are different laws of physics. As scientists, we could imagine trying to discover this difference by performing experiments. In addition to the initial and boundary conditions, we would want to set something like
as an exception to the normal wave function. (The wave function does not apply to this point because we arbitrarily forced it to be true.)
Then, rule would give

and rule would give
which are clearly different and we can lear which physics actually applies.
If we were beings inside of this universe, enforcing a grid square to disobey the general rule might not be possible. As beings outside of this universe, we can do it: we have the power to select an actual world from the set of possible worlds. (This is an application of Pearl's do-calculus, in which you can discover the causal structure by forcing an event, breaking its inward causal links.)
There's a big difference between the raw grid cell values, which are given by nature, and the causal arrows that we draw on top of them. The grid cell values are an external reality—they are what they are, and maybe have patterns among them that could be described by equations, maybe not. The arrows are a model of the physical reality, explaining it, and we can ask questions of the model that we may not be able to ask in real life.
In the same sense, the physical reality we find ourselves in is a different reality-box from models about it, including causal explanations and reasons-why more generally. We can contemplate a suite of possible worlds that all obey a given rule, but only one of those is the actual world. This can even account for the difference we make between past and future: we can contemplate a suite of possible worlds about future events and not past events because we know the actual world of the past to a greater degree than the future. In the physical reality, however, the future is as classically determined or quantum mechanically random as the past.
Models, causality, possibilities, and an open future are all overlaid on the physical world. But just as mathematics is neither more real nor less real than the physical world, this world of causality and reasons-why is just as real and respectable as the physical world. True reasons-why, such as the reason why the 8-ball fell into the billiards table pocket, have a degree of undeniableness to them, which seems to be the unifying feature of all these definitions of reality.
Reality 4: conventional
Even further from the objective physical and mathematical worlds, but no less real, some things are true because everybody (or enough people) think that they are.
For example, money exists. Money has an undeniableness that is strictly due to the fact that enough people take it seriously. Different currencies change their values because people, on average, change their opinions about how much they'd be willing to exchange for them. Money is a social convention, but a powerful one: just like denying the existence of a large stone, basic logic, or the causal effect of gravity, denying that you owe somebody money can have significant consequences.
Right away, it should be clear that this truth-by-convention is not the same as the other reality-boxes. It is not objective—someone from a different culture can come to a different conclusion about whether money is real and how the money-game may be played. In fact, different cultures have had a lot of different notions about how money works. Based on this lack of objectivity, one might be tempted to say, "Money does not exist," and implicitly mean that it doesn't matter because it is not a universal reality.
But ignoring conventional truths and social constructs would exclude an awful lot. Remember that the only thing I could say about the physical existence of my pencil is that there's a blob of material ("stuff") there. The properties of the particles inside the volume of what I call the pencil differ somewhat from what I call the surrounding air, but only in general, since molecules are constantly chipping off and glomming on. The pencil flows into the surrounding air, and the surrounding air flows into the pencil. Disregarding convention, I could divide the space differently, identifying every even numbered atom of the pencil as one object and every odd numbered atom as another. Or every even numbered atom and the northern hemisphere of the moon could be another object.
We don't often consider these crazy groupings of atoms because we'd lose the ability to reason about anything at human scales. And not just human scales—there's a hazy line between galaxies and galactic superclusters, and even the smallest particles are partially defined by convention. For instance, what low-energy physicists call a photon (a particle of light) is, in the Standard Model, an admixture of two field-particles. In one basis (a choice of orientation angle in the Standard Model's group geometry), the coordinate is a photon and the coordinate is a Z boson. That basis is a natural choice for most low-energy problems because of the omnipresence of a Higgs field, but fundamentally, it's just one choice of basis. At energies much larger than the Higgs mass, we'd pick a different basis.
And then there's language. The distinction between phonetics, the continuum of sounds that we make, and phonemics, their discrete units of meaning—such as the 44 sounds in the English language—is a distinction between physical facts and conventional facts. Different languages have different numbers of sounds and draw the lines between them differently. Hindi has 4 sounds that resemble the English "t" but 1 sound that could be "v" or "w". Before writing off language as "not real," consider that we wouldn't be able to talk about any other reality without it. This essay is itself an attempt to redraw—and hopefully sharpen—the boundaries between different uses of one word in particular, "reality."
For another example, software development is little more than building and agreeing upon conventions—a social construction! The most fundamental layer of software is an idealized machine: a linear memory bank of bits 0 and 1, some registers or a stack (temporary memory), and a sequence of instructions that perform deterministic transformations on those bits. (By convention, we ignore the possibility of transistor charge leakage and bit-flipping by cosmic rays.) But hardly any software development operates in these terms: there is a tower of low-level languages, high-level languages, application frameworks, etc. between most developers and the raw bits, and all of those abstractions are agreements between developers about what they should consider correct and what they should consider incorrect.
In fact, software development is a great example of property dualism, in which high-level concepts like "function," "file," and "menu item" supervene on lower-level concepts. A high-level property, such as "this file is empty," supervenes on the bits-on-disk because if the high-level property changes, it must be accompanied by a change in the low-level bits-on-disk. Making the file contain the phrase "hello world" necessarily involves some bits-on-disk becoming different from their previous state. The reverse doesn't have to be true: different bits-on-disk can correspond to the same state of the file being empty. (Suppose that the operating system reserves some space for the file to grow, alongside an integer counting the number of meaningful bytes, which is initially set to zero. The operating system might reserve 4 kB, 8 kB, or any other number of bytes, filled with any junk bytes, and it would still be considered an empty file.)
To the extent that programming is not just getting something to work, but getting things to work together, most of the substance of software development is agreeing upon and adhering to conventions. Even the parts of a program that don't talk to other programs talk to the user of the software, who has to interpret the high-level concepts in a conventional way. If a user can't recognize or chooses to not recognize the distinction between a drop-down menu and a scroll bar, the program wouldn't work for that user. In a sense, the program wouldn't even exist for them. All of a programmer's effort comes to nothing if the user doesn't play along, just as a millionaire loses everything if everybody else stops believing in money.
Thus, social constructs are real, and many of them run so deep that they might not look like constructs. But they clearly represent a different reality-box from the physical, mathematical, and narrative realities—as different from them as they are from each other.
Reality 5: subjective
Subjective reality is the experience of life in the first person. Like mathematical reality, it is a priori, but unlike mathematical reality, the referents of statements don't have a self-consistency that can be independently verified. You just have to trust me when I say that I experience quale (the way paper feels, to me, what it's like to drink coffee, for me, and so on). It shouldn't be too difficult to trust me, since you must be experiencing these things, too, possibly in a different way. Short of telepathy, we'll never even know how similar or different our experiences of these things are, though it's reasonable to assume that they at least exist.
Since the things this reality-box are not communicable, they're also the most contentious. Some people say that conscious experience is an illusion, that there is no subjective experience at all. That statement couldn't mean what it sounds like it means, since illusions are things that only subjective beings can experience.
To illustrate, consider the following situations:
- An arrow shot from a bow fails to hit its target because it was pointed the wrong way when it was released.
- A gradient descent algorithm fails to find the global minimum of a function because it started in a local well.
- A (non-AGI!) robot vacuum fails to clean part of a room because it was programmed with rectangular models of rooms, and the room is not rectangular.
- A highly advanced neural network (possibly AGI) fails to generalize from its training dataset.
- An alien who has traveled to Earth fails to understand human emotions.
- I think I see water in the desert, but it is a mirage.
In this series, most people would not say that the arrow was suffering an illusion about where the target is, and most people would say that I'm suffering an illusion about water in the desert. Where we draw a line or if we draw a sharp line in the series may vary, but we're more likely to use the word "illusion" for the later cases because there's a being, with agency, capable of being deceived or mistaken. If you had, for instance, a highly intelligent arrow that can hold conversations with you and can direct itself mid-flight, then maybe you'd say that that arrow suffered an illusion about where the target is. Simply using the word "illusion" is suggestive that we're talking about subjective reality.
Perhaps when people say that conscious experience is an illusion, they're meaning something analogous to, "The existence of my pencil, as a pencil and not just a glob of matter, is a conventional reality and not a physical reality." This is why it's so useful to have these different reality-boxes! It certainly seems to be the case that our minds are implemented as brains, just as a pencil is made of atoms, and the pencilness is something asserted about the atoms (the conventional reality) that's not in the atoms themselves (the physical reality).
In my definition of subjective reality as the "experience of life in the first person," I'm also trying to avoid words like "existence of a self," since there's a long tradition in Buddhism rejecting that particular idea. Although Buddhists reject the idea of a permanent, soul-like self (ātman/आत्मन्), they also distinguish between conventional truth and ultimate truth, and conventionally use the words "I" and "me." I don't think they would deny that we experience life from a first person perspective, just that that experience is not an ultimate reality (if one exists, a disagreement between Theravada and Mahayana Buddhists), just as I'm distinguishing subjective reality from physical reality. A traditional explanation of self in Buddhism compares it to a chariot, and the chariot is not the wheels, not the axel, not the seat, etc.—the subjective experience exists, but it's not a fundamental particle.
There's a circular irony in the relationship between physical reality and subjective reality that I like to think of as a fight between a physicist and a neurologist. Imagine a physicist who takes her status as a rational being as a starting point, assumes that she is making free choices in the design of her experiments, and believes enough of her sense perceptions to interpret the experimental measurements. In doing so, she develops the physics of medical imaging machines. The neurologist then takes the medical imaging machines and uses them to study the physicist's brain. He applies external stimuli, various drugs, electric shocks, (lesions?!?) and eventually comes to the conclusion that the physicist is a chemical machine that responds to its environment: looming conference deadlines cause her to type up physics papers.
Who do we believe? To the physicist, the physical world is a thing she learned about by applying her subjective experience as a given. To the neurologist, the mind is a thing built up from the physical world. It is as though one is inside the other, and the other is inside the one.
Conclusion
That's why I think it's necessary to think about these different types of realities without a hierarchy between them, without privileging one as "really real" and the others as "a manner of speaking." This is a non-monist point of view, like Descartes's dualism, except that I've listed at least five realities, not two. It's also unlike Descartes's dualism in that Descartes imagined two fundamental substances—position-independent res cognitas that minds and angels are made out of and position-dependent res extensa that unthinking matter is made of. In my terminology, these would both go into the physical reality-box, since res cognitas is objective "stuff" like matter. (Lack of location and extension is not unthinkable in a physics theory. Luminiferous aether was expected to be an impalpable solid, dark energy is posited to be a fluid with negative pressure, and all theories of quantum gravity break down the idea of location in real-valued coordinates in some way. We're fine with exotic substances.)
The different meanings for "real" and "to exist" that I've presented here are qualitatively different from each other. They're different language-games, as though we have at least five things we want to talk about and frustratingly use the same word for all of them. There's a psychological appeal in simple theories (unified field theory, anyone?) that may motivate monism, but I'd rather go for clarity over unity. It seems like many "X exists!"/"X does not exist!" arguments are just crossing their terms.
As I said at the beginning, I don't think we're limited to these five, either. I alluded to a general category of narrative truth, or reasons-why, but only talked about causality because it's the most precise kind of reason why. Aristotle described four kinds of causality, most of which lack the if-then structure that seems to be necessary in the modern use of the word:
- The material cause of a table is what it's made out of, such as wood.
- The formal cause of a table is the shape that it has: flat on top and supported underneath.
- The efficient cause of a table is what made it: a carpenter.
- The final cause of a table is what it was made for, such as dining.
It seems like Aristotle is explaining "why a table exists" in four different ways, rather than specifically if-then logic, like "If the king requests a table, then the royal carpenter will make one." Scientists and mathematicians are also very interested in explaining-why, as a narrative, rather than just explaining what they measured or proved. For example, the theorem "223893150340 + 8859134642 = 232752284982" is true and has never before appeared in print, but it's not interesting because it doesn't explain anything new. It's not a new story about math, such as an unexpected connection between seemingly disparate mathematical objects.
Also, I never mentioned ethical or moral values, and it may be that statements like, "Decreasing everybody's happiness is wrong," are true statements. They have some level of undeniableness, like all of the other reality-boxes. But are they different from aesthetics ("I like blue paintings")? Are they distinct from emotions ("Decreasing everybody's happiness makes me feel bad")? Are any of them objective like mathematics and maybe some narratives, or are they all conventional truths, true only because of agreement? Do they belong to yet another reality-box?
I'm leaving it open because I'm not sure. In this essay, I only want to make the point that there are different reality-boxes, not what all the reality-boxes are.