Why does gradient descent always work on neural networks?
32lalaithion
8Daniel Kokotajlo
17Donald Hobson
6winstonBosan
2JenniferRM
2Thomas Kwa
6Ilio
2JenniferRM
2jacob_cannell
3Donald Hobson
1james.lucassen
New Answer
New Comment
4 Answers sorted by
320
High dimensional spaces are unlikely to have local optima, and probably don’t have any optima at all.
Just recall what is necessary for a set of parameters to be at a optimum. All the gradients need to be zero, and the hessian needs to be positive semidefinite. In other words, you need to be surrounded by walls. In 4 dimensions, you can walk through walls. GPT3 has 175 billion parameters. In 175 billion dimensions, walls are so far beneath your notice that if you observe them at all it is like God looking down upon individual protons.
If there’s any randomness at all in the loss landscape, which of course there is, it’s vanishingly unlikely that all of the millions or billions of directions the model has to choose from will be simultaneously uphill. With so many directions to choose from you will always have at least one direction to escape. It’s just completely implausible that any big model comes close to any optima at all. In fact it’s implausible that an optimum exists. Unless you have a loss function that has a finite minimum value like squared loss (not cross entropy or softmax), or without explicit regularization that bounds the magnitude of the values, forces positive curvature, and hurts performance of the model, all real models diverge.
Source: https://moultano.wordpress.com/2020/10/18/why-deep-learning-works-even-though-it-shouldnt/
Wait, how is it possible for there to be no optimum at all? There's only a finite number of possible settings of the 175 billion parameters; there has to be at least one setting such that no other setting has lower loss. (I don't know much math, I'm probably misunderstanding what optimum means.)
Taking finite precision floating point numbers, there must be an optimum.
In the real numbers, there are an infinity of possible settings. Its possible to have an infinite sequence of ever better solutions. (The trivial example is the bigger a parameter is, the better the results, for any setting, its possible to add 1 and get a better setting.)
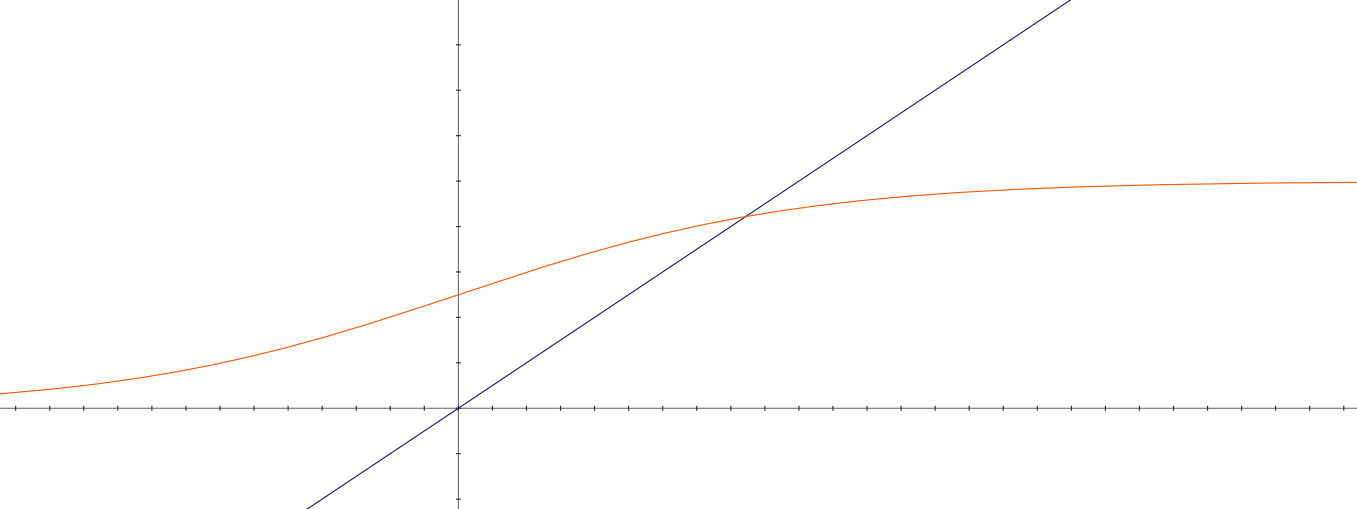
Its possible for the score to behave like the blue line. Getting better and better without bound. Its also possible for the score to behave like the orange line. With some finite value it approaches but never reaches.
6
Agreed, there can be a optimum. But I think the intuition here is that it is exceedingly rare enough to run into a situation where it is local optima in all "directions".
It is only an "optimum" when all 175 billion parameters are telling you to screw off and stop trying.
2
There can be N settings that perfectly tie for the best score.
Also, they might exist in neighborhoods that are also very very very high scoring, such that incremental progress into any of those neighborhoods makes the optimal function local to the optimizer.
...
One thing that helps me visualize it is to remember circuit diagrams. There are many "computing systems" rich enough and generic enough that several steps of "an algorithm" can be embedded inside of that larger system with plenty of room to spare. Once the model is "big enough" to contain the right algorithm... it doesn't really pragmatically matter which computing substrate parts are used to calculate which parts of The Correct Function Given The Data.
Another helpful insight is an old chestnut that Ilya always stuck in his talks back in the day (haven't seen a talk lately (maybe he's still doing it?)) about how a two-layer neural net can learn integer sorting.
I assume the neural net must discover some algorithm that either "just is radix sort" or else is similar to radix sort, which is a linear time sorting algorithm that can get away with computing SORT in linear time by having a maximum value. (I've never personally tried to train a net to do this, nor tried to figure out how and why the weights worked after training them.)
But basically: these systems can do fully generic computation and can learn which part of "fully generic computation" is approximately The Correct Function based on the labeled data.
...
Also, they often have some regularization built in generally (because it often makes it go faster?) so that there is a penalty for "complicated models". This makes overfitting much less common in practice, especially on real problems where there's really something non-trivial to learn that is hiding in the data.
The lower level "stuff out of which the learning is made" becomes less important eventually, due to that "stuff" being optimized to be sufficient to learn whatever the learning sub
2
I think the linked post is assuming that the parameters are real numbers.
I'm still confused by "Unless you have a loss function that has a finite minimum value like squared loss (not cross entropy or softmax)" because cross entropy is bounded below at zero.
60
It may be the deepest thing we understand about NN (but I might got stoned for suggesting we actually know the answer). See lalaithion’s link for one way to see it. My own take is as follow:
First, consider how many n-sphere(s) of radius slightly below 1/2 you can pack in a n-dimensional unit cube. When n is low, « one » is the obvious answer. When n is high, the true answer is different. You can find the demo on internet, and if you’re like me you’ll need some time to accept this strange result. But when you do, you will realize high dimensions means damn big, and that’s the key insight.
Second, consider that training is the same as looking for a n-dimensional point (one dimension for each weight) in a normalized unit cube. Ok, you got it now: gradient-descent (kind of) always work in high dimensions because high dimensions means a damn big number of possible directions and quasi-solutions, so large that by pigeonhole principle you can’t really have dead ends or swamp traps as in low dimensions.
Third, you understand that’s all wrong and you were right from the start: what we thought were solutions frequently present bizarre statistical properties (think adversarial examples) and you need to rethink what generalization means. But that’s for another ref.
20
Partly it might be because it often is not "just" pure gradient descent. There are tweaks to it, like AdaGrad, that are sometimes used? These might be mostly about cost though. Getting to a "good enough answer" as quickly and cheaply as you can tends to be a relevant criteria of "practical success" in practical environments.
20
The quality of a neural network comes from its size, shape, and training data, but not from the training function, which is always simple gradient descent.
Only if you consider modern variants of batch Adam with momentum, regularization, etc to be 'simple gradient descent'.
Regardless SGD techniques are reasonable approximations to bayesian updating with numerous statistical limiting assumptions, which fully explains why they work when they do. (And the specific limiting assumptions in said approximation sufficiently explain the various scenarios when/where SGD notoriously fails - ie handling non-unit variance distributions, etc).
Most of the other possibilities (higher order techniques) trade off computational efficiency for convergence speed or stability, and it just happens that for many economically important workloads any convergence benefits of more complex methods generally aren't worth the extra compute cost; it's instead better to spend that compute on more training or a larger model instead.
I suspect that eventually will change, but only when/if we have non-trivial advances in the relevant efficient GPU codes.
Here's a good related reddit thread on proximal-point based alternatives to gradient methods.
Rendering 2/6 comments, sorted by (show more) Click to highlight new comments since:
It doesn't always work when the goal is to find a good enough answer. When it fails, you fiddle with something and try again. You sure aren't getting optimal large datasets. On many large problems, each piece of training data is only used once. This means the first few steps are applied to randomness, and the last few steps can only make a tiny change.
Actually, there are momentum methods, ADAM etc that are often used instead of gradient descent.
it doesn't work if your goal is to find the optimal answer, but we hardly ever want to know the optimal answer, we just want to know a good-enough answer.
Also not an expert, but I think this is correct
Curated and popular this week