This is a link post for a Substack post I made, which itself is a remaster of set of messages I sent in another forum, because I thought it was important enough to deserve being publicized properly.

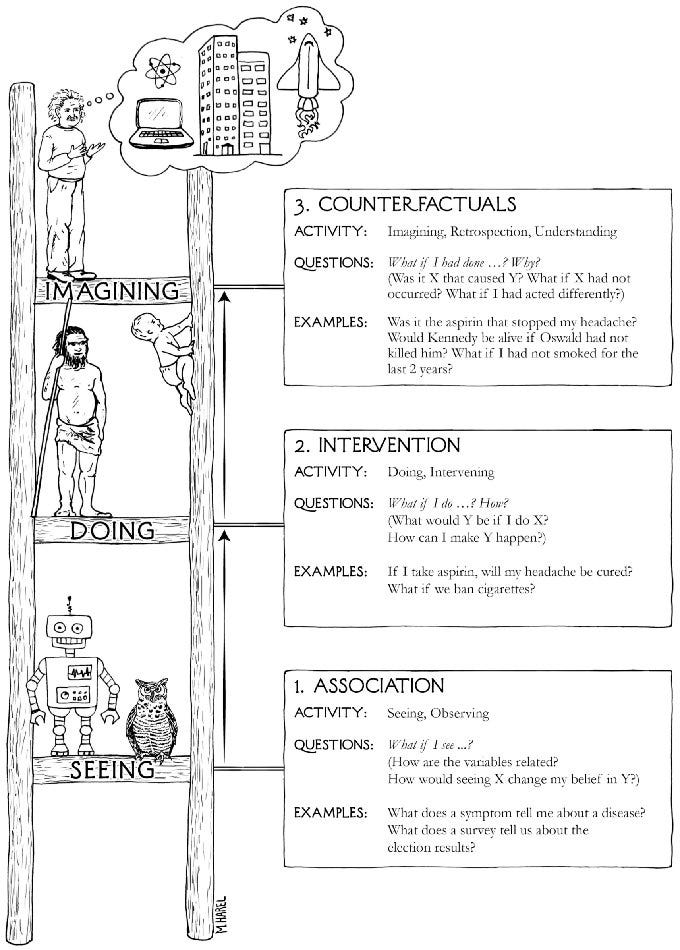
Let’s start with some philosophy of causality, specifically a quick review of Judea Pearl’s Ladder of Causality. Imagine that you want to build a suspension bridge, and you need to get a cable that doesn’t break for the bridge. How could you go about doing this?

One possibility would be to look at historic cases where suspension bridges broke, and try to figure out how they differ from cases where bridges didn’t break. Maybe breaking bridges tend to use cheap rather than expensive materials, so you get an extra-expensive cable made of a gold alloy to be on the safe side. Maybe they tended to be built in places with many records of large storms, and break shortly after meteorologists warn of a new hurricane, so you destroy the historical records and get rid of the meteorologists in the area.

These solutions are obviously terrible. The issue is that the associations above is not causation; while you can probably find statistical tendencies with material costs or storm warnings correlating with bridge crashes, you can’t intervene on these variables to prevent the bridges from crashing; they’re only correlated with bridge stability due to them being side-effects of other factors. They are mere correlations, which in Judea Pearl’s causal ladder would be called rung 1.

We need a causal understanding of the world, both for decision-making and for many forms of theory and research. Causality is ultimately about counterfactuals or potential outcomes; the ability to consider not just what happens, but also what would happen differently if some variable had been different. But how can we know this? The answer is that it can be computed if we have an appropriate causal model of the world.

For instance, if you know the strength of a cable, you know how much load it can bear until it deforms or breaks. If you know how much load the bridge will put on the cable, you can know whether any given cable will break, and can select a cable that causes the bridge to keep standing. Further, if the bridge collapses, you might be able to figure out the load that was on the bridge at the time, and see whether the bridge broke because of an insufficiently strong cable. A theory that allows these kinds of inquiries is called a rung 3 theory.

But designing a bridge is hard. Maybe if you are a civil engineer, you can do it. But otherwise, you probably hire an engineer to do it for you. In order to do so, you must choose which engineer to hire. This may make a difference if engineers vary in quality; maybe a bad engineer could cause your project to fail. But wait - you can’t compute the potential outcomes of the bridge for different engineers, so in what sense can you really say that it matters what engineer you choose? The answer to this is what this blog post will explore, and in particular it turns out that there is a notion of causality that shares the nondeterminism of rung 1 with the causality of rung 3, which is called rung 2.

How is this relevant for social science? Well, social scientists often, implicitly or explicitly, make causal claims. E.g. that education improves future income, that intelligence is influenced by genes, that income inequality between races is due to racism, that people get a good idea about what your personality is like by interacting with you, that traumatic events worsen your mental health, etc..

It’s important to understand that these claims are merely rung 2 causal claims, as I have seen people dismiss them because they don’t fit the strict standards expected of rung 3 causal claims. Conversely, I think it’s also important for people who are perfectly comfortable with rung 2 causal claims to understand the difference from rung 3 causal claims, so they can better understand why people might object to them for lacking determinism.

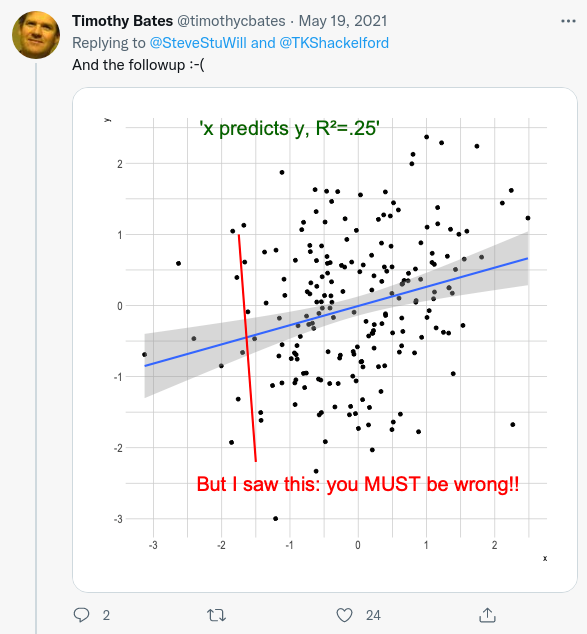
I personally used to entirely dismiss people who made arguments about lack of deterministic relationships, but after getting a better understanding of rung 2 vs rung 3, I now find the objections much more reasonable, and have started paying lots of active attention to determinism or lack thereof. I cannot cover everything about the distinction here, but I can do a partial overview.

Rung 3 - Individual-level causality

The defining feature of rung 3 causality is determinism. Some initial variables go in, and an outcome comes out. The determinism makes it possible to evaluate what outcome you would have had if some of the variables had been different. The basic building blocks of rung 3 causal models are structural equations, which are equations of the form:

z := f(x, y)

That is, structural equations are equations which describe a variable z as a function f of some set of causes x, y, …. When you then want to figure out the effects of one of the causes, you do so by computing a counterfactual, where you replace the variable of the cause with a new value - e.g. f(1, y) - f(0, y) tells you the effect on z of changing x from 0 to 1, for a given y level.

Why should we care about rung 3 causality? Here’s three reasons:

• Most of everyday life causality is rung 3. If you’re baking a loaf of bread and it gets burnt, you can imagine that if you had left it in the oven for a shorter time, or at a lower temperature, it would not have been burnt. If you pull out a chair to sit on, you can predict that it will move according to your force. And so on.
• Rung 3 is the true causality. The physical world is mostly a deterministic system. There may be practical matters which prevent us from fully predicting it; but in principle it seems appropriate to imagine that the underlying real process that generated the data we are working with lies in rung 3.
• Determinism protects against certain causal inference problems. Consider confounding; you may observe a correlation between two variables even though there is no causal relationship, if there is another variable that causes both. However, if you can deterministically predict a system, you know you are not missing any important variables.

But perhaps the most important thing about rung 3 causality is that social science cannot successfully determine rung 3 models.

The inherent nondeterminism of social science

First problem: heterogeneity. Consider, for instance, the case of education improving one’s income. Maybe it improved your income, but at the same time there are some tech startup founders who dropped out of education and got rich creating highly valued tech products. It seems like if they had stayed in the education system for longer, they could plausibly have missed the chance of creating the startup and earning the money. So for them, more education would have reduced their income.

Heterogeneity is not necessarily a problem, if you can predict the heterogeneity. But social scientists can’t do that, due to the second problem.

Second problem: chaos. Causality is about what would have happened if some variable had been different. But most complex systems are highly sensitive to initial conditions, such that even an infinitesimal change to the initial variables will lead to entirely different outputs. (This, by the way, is the reason that weather forecasts only work for a short timespan.) For an example of how chaos appears, you can see this video of many nearly identical double pendulums, showing how even tiny changes can lead them to completely different trajectories:

Social scientists can’t predict people’s lives or society’s trajectory, and a large part of this difficulty is probably due to chaos. But if you can’t predict what actually happens, how could you ever hope to predict how things would be different if some variable had been different? Since rung 3 causality requires deterministic relations, this makes rung 3 impossible.

Defining rung-2 causality

Let’s consider a concrete example; the genetic heritability of intelligence. I’ll ignore the question of how to measure intelligence - a topic for another blog post - and just assume we have some reasonable measure. Though as mentioned in the start of the post, almost any social science topic would be applicable here.

Social scientists claim that intelligence has a substantial genetic component. But this doesn’t make sense in terms of rung 3 causality, because we cannot separate the genetic component from the environmental component, and because intelligence is probably too chaotic to be predictable. But imagine that we did have a rung 3 causal model of intelligence. We might imagine that it looks like this

intelligence := f(genes, environment)

With f being some unknown, presumably very complicated function, which describes the results of the development of human intelligence. In this hypothetical, I’ve split the inputs to f into genes and environment, which you might think of as referring to the DNA passed onto you by your parents at conception, vs the state of the rest of the universe at that time. The “inputs” to f could be split in many ways other than this, and a complete theory would probably split them in a very different way than I describe here, but it’s just a hypothetical example.

If f was linear, it would in principle be straightforward to attribute causation; just use the coefficients associated with each input as your quantities for the strength of causation. (In practice, figuring out the linear coefficients for f would be a difficult undertaking in itself.) But in reality, f is probably nonlinear and chaotic; you can’t just separate genetics and environment, and you can’t predict someone’s intelligence before they’re born, decades in advance of testing it.

This not only makes it hard to figure out what f is, it also makes it hard to define the effect of someone’s genes on their intelligence. Suppose for instance you have two people:

• Alice, who is temperamentally studious and curious, but who was raised in an impoverished environment with no access to education and constant threat of malnutrition
• Bob, who is does not care much for learning, but likes to do drugs, and who was raised in a rich and stimulating environments, which gives him ample opportunity for learning, but which he squanders and instead uses to fry his brain in a thick mist of drugs

Alice’s intelligence outcome can be described as intelligence_Alice := f(genes_Alice, environment_Alice), while Bob’s intelligence outcome can be intelligence_Bob := f(genes_Bob, environment_Bob). Presumably, the effect of their genes on their intelligence is defined as the difference for f over the different genetic possibilities:

genetic effect(environment) = f(genes_Alice, environment) - f(genes_Bob, environment)

But the trouble is; what environment should we hold constant to define the genetic effect? After all, conceivably, in Alice’s environment, their genes would not make much of a difference regardless, due to the lack of opportunity. Maybe genetic effect(environment_Alice) is close to 0 IQ. Meanwhile in Bob’s environment, they might make a much bigger difference, due to the greater number of opportunities, so maybe genetic effect(environment_Bob) is 30 IQ.

The problem is that this only defines genetic effects if we fully control for the environment, which seems basically impossible. So again, what can we do?

If we have a distribution of environments, one thing we can talk about is the average effect across different possible environments. So in the hypothetical case with the two environments, that would give:

average genetic effect = ½ (genetic effect(env._Alice) + genetic effect(env._Bob))

It seems to me that this quantity does tell us something about the genes involved; it’s not unreasonable to call this a measure of the genetic effects on intelligence. So concepts like this makes it in principle meaningful to talk about causal effects, even for systems you can’t predict. In particular, it’s important to emphasize that this is the very same notion of causality as we had in the deterministic predictable case - except that it is just averaged over different contexts.

More generally, for any unpredictable system, while you cannot necessarily talk about the causal effects in individual cases in a useful way, you can still often talk about the average effects, aggregating the individual causal effect over some distribution of contexts.

Estimating rung-2 effects

Of course, these sorts of definitions are not immediately very useful. After all, it’s not clear that the previously defined average effect can be estimated through any method other than figuring out the rung 3 deterministic causal model f, and computing the appropriate averages. But this is where statistics and the field of causal inference comes in.

For instance, suppose hypothetically your system is determined as an unknown function f of exactly two variables:

z := f(x, y)

In this case, if you have a distribution of data (x, y, z) where x and y are statistically independent, you can estimate the average effect of x and y using linear regression, without knowing the details of f. This allows you to bypass the problem of a potentially highly complex and unpredictable function, and get an idea of some rough pattern of effects.

Of course, often things won’t be as straightforward as this; often the different input variables won’t be statistically independent, and often we won’t even know what all of the different input variables are. The causal inference literature has come up with a toolbox of different methods that can be used under different conditions, though often they cannot quite estimate the average causal effects, but instead only some modified version (which may still tell you about causality, but in a way which is only guaranteed to be accurate for a certain subgroup).

In the specific case of untangling the aggregate effects of genes, there has been invented a rich set of methods, including twin studies, adoption studies, within-family polygenic score regression, relatedness disequilibrium regression, and more. All of these have different advantages and disadvantages, and they all rely on different assumptions and provide different kinds of bounds.

The complexity in the previous paragraph gives another important lesson: There is an incredible amount of detail to learn about each topic where you are trying to investigate rung 2 causal effects. You need to learn the assumptions that each method makes, and then learn how plausible those assumptions are (both a priori and according to studies which directly investigate the assumptions), and how big of a skew it would introduce if the assumptions were broken.

In the limit, rung 2 becomes rung 3

Couldn’t we just skip past rung 2 and go directly to rung 3?

Not really; as mentioned earlier, chaos might mean that we can’t ever reach rung 3 in social science. But also, even if it wasn’t for chaos, the main way it seems like we could start approaching rung 3 would be to investigate each factor with rung 2 methods, until we find a set of factors that are sufficiently powerful so as to allow us to predict the outcome in a rung 3 manner. After all, we don’t just magically know what variables are relevant until we start investigating, and we can’t look at all variables in the universe at once.

As such, if we want to do iterative science, we need to start with rung 2 causality and build upwards, maybe eventually reaching rung 3 under certain circumstances.

Thanks to Justis Mills for proofreading and feedback about the coherence of the post.