Snake Eyes Paradox

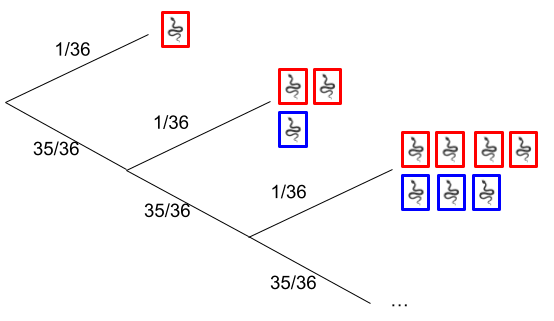
Calculating the odds of dying when playing the snake-eyes game with a player base of arbitrary size.

For an arbitrary player base of players, the maximum possible rounds that the game can run is then the whole number part of $L o g_{2} (B)$ , we will denote the maximum possible number of rounds as $m$ .

We denote the probability of snake-eyes as $p$ . In the case of the Daniel Reeves market $p = 1 / 36$ .

Let $D_{n} =$ the probability density of the game ending in snake-eyes on round n then $D_{n} = p (1 - p)^{n - 1}$ .

The sum of the probability density of the games which end with snake eyes is

$= m \sum n = 1 D_{n}$

$= m \sum n = 1 p (1 - p)^{n - 1}$

$= p m \sum n = 1 (1 - p)^{n - 1}$

$= p \frac{1 - (1 - p)^{m}}{1 - (1 - p)}$

$= 1 - (1 - p)^{m}$

The sum of the probability densities of the games ending in snake-eyes is less than $1$ which means that the rounds ending in snake-eyes does not cover the full probability space.

Since there are finitely many dice rolls possible for our population there is always the possibility that the game ends and everyone won. This would require not rolling snake-eyes $m$ times and has a probability density of $S_{m} = (1 - p)^{m}$ which is exactly the term we need to sum to $1$ giving us full coverage of the probability space.

Note: That $D_{m} + S_{m}$ are the probability densities of the final round ending in a loss or ending in a win and must there for equal $(1 - p)^{m - 1}$ the probability of getting to round $m$ by the players winning the prior $m - 1$ rounds.

Here we verify that $D_{m} + S_{m} = (1 - p)^{m - 1}$

$D_{m} = p (1 - p)^{m - 1}$

$S_{m} = (1 - p)^{m}$

$D_{m} + S_{m} = p (1 - p)^{m - 1} + (1 - p)^{m}$

$= p (1 - p)^{m - 1} + (1 - p) (1 - p)^{m - 1}$

$= [p + (1 - p)] (1 - p)^{m - 1}$

$= (1 - p)^{m - 1}$

Denote the number of players in each round $n$ as $P_{n} = 2^{n - 1}$

Denote the total number of players chosen in a game that ends at round $n$ as $T_{n} = 2^{n} - 1$

The probability of losing given that you are chosen to play can be computed by dividing the expected number of players who lost (red-eyed snakes) by the expected total number of players chosen.

First we will develop the numerator of our desired conditional probability. What is the expected number of players who lose in a game, given that cannot go beyond $m$ rounds? This will be the sumproduct of the series of players in each round $n$ and the series of probability densities of the game ending in round $n$

$m \sum n = 1 P_{n} D_{n} = m \sum n = 1 2^{n - 1} p (1 - p)^{n - 1} = p \times \frac{1 - 2^{m} (1 - p)^{m}}{1 - 2 (1 - p)}$

Now we will develop the numerator of our desired conditional probability. What is the expected total number of people chosen to play? This will be the sumproduct of the series of total players in a game ending in round $n$ and the series of probability densities of the game ending in round $n$ .

$(m \sum n = 1 D_{n} T_{n}) + S_{m} T_{m} = (m - 1 \sum n = 1 D_{n} T_{n}) + (D_{M} + S_{m}) T_{m} = (m - 1 \sum n = 1 D_{n} T_{n}) + (1 - p)^{m - 1} T_{m}$

$= (m - 1 \sum n = 1 p (1 - p)^{n - 1} (2^{n} - 1)) + (1 - p)^{m - 1} (2^{m} - 1)$

$= p (m - 1 \sum n = 1 2^{n} (1 - p)^{n - 1} - m - 1 \sum n = 1 (1 - p)^{n - 1}) + (1 - p)^{m - 1} (2^{m} - 1)$

$= p (2 m - 1 \sum n = 1 2^{n - 1} (1 - p)^{n - 1} - m - 1 \sum n = 1 (1 - p)^{n - 1}) + (1 - p)^{m - 1} (2^{m} - 1)$

$= p (2 \times \frac{1 - 2^{m - 1} (1 - p)^{m - 1}}{1 - 2 (1 - p)} - \frac{1 - (1 - p)^{m - 1}}{1 - (1 - p)}) + (1 - p)^{m - 1} (2^{m} - 1)$

Combining the numerator and denominator into the fraction we seek we now have

$\frac{E (L o s e)}{E (P l a y e d)} = \frac{\sum_{n = 1}^{m} P_{n} D_{n}}{(\sum_{n = 1}^{m} D_{n} T_{n}) + S_{m} T_{m}} = \frac{p \times \frac{1 - 2^{m} (1 - p)^{m}}{1 - 2 (1 - p)}}{p (2 \times \frac{1 - 2^{m - 1} (1 - p)^{m - 1}}{1 - 2 (1 - p)} - \frac{1 - (1 - p)^{m - 1}}{1 - (1 - p)}) + (1 - p)^{m - 1} (2^{m} - 1)}$

Note: that since it is impossible to lose unless you play the conditional probability is equal to the above ratio.

$P (L o s e | P l a y e d) = \frac{P (L o s e \cap P l a y e d)}{P (P l a y e d)} = \frac{P (L o s e)}{P (P l a y e d)} = \frac{E (L o s e)}{E (P l a y e d)}$

And then we thank WolframAlpha for taking care of all the algebraic operations required to simply this fraction, see alternate form at : https://www.wolframalpha.com/input?i2d=true&i=Divide%5Bp*Divide%5B1-Power%5B2%2Cm%5DPower%5B%5C%2840%291-p%5C%2841%29%2Cm%5D%2C1-2%5C%2840%291-p%5C%2841%29%5D%2Cp%5C%2840%292*Divide%5B1-Power%5B2%2Cm-1%5DPower%5B%5C%2840%291-p%5C%2841%29%2Cm-1%5D%2C1-2%5C%2840%291-p%5C%2841%29%5D-Divide%5B1-Power%5B%5C%2840%291-p%5C%2841%29%2Cm-1%5D%2C1-%5C%2840%291-p%5C%2841%29%5D%5C%2841%29%2BPower%5B%5C%2840%291-p%5C%2841%29%2Cm-1%5D%5C%2840%29Power%5B2%2Cm%5D-1%5C%2841%29%5D

We find that the conditional probability of losing given that you are chosen to play from a arbitrary population of players is simply $p$ . The size of the population was arbitrarily selected from the natural numbers so as the population goes to infinity the limit will also be $p$ .

$P (L o s e | P l a y e d) = p$ $\forall$ $n \in N$ therefor the limit of our conditional probability is $lim n \to \infty p = p$

[-]Primer2y21

"The sum of the probability densities of the games ending in snake-eyes is less than 1 which means that the rounds ending in snake-eyes does not cover the full probability space."

This is contradicted by the problem statement: "At some point one of those groups will be devoured by snakes", so there seems to be some error mapping the paradox to the math.

[-]Wamba-Ivanhoe2y*63

I posit that the supposition that "At some point one of those groups will be devoured by snakes" is erroneous. There exists a non-zero chance that the game goes on forever and infinitely many people win.

The issue is that the quoted supposition collapses the probability field to only those infinitely many universes where the game stops, but there is this one out of infinitely many universes where the game never stops and it has infinitely many winners so we end up with residual term of . We cannot assume this term is zero just because of the $\infty$ in the denominator and disregard this universe.

[-]dreeves2y*80

"At some point one of those groups will be devoured by snakes" is erroneous

I wouldn't say erroneous but I've added this clarification to the original question:

"At some point one of those groups will be devoured by snakes and then I stop" has an implicit "unless I roll snake eyes forever". I.e., we are not conditioning on the game ending with snake eyes. The probability of an infinite sequences of non-snake-eyes is zero and that's the sense in which it's correct to say "at some point snake eyes will happen" but non-snake-eyes forever is possible in the technical sense of "possible".

It sounds contradictory but "probability zero" and "impossible" are mathematically distinct concepts. For example, consider flipping a coin an infinite number of times. Every infinite sequence like HHTHTTHHHTHT... is a possible outcome but each one has probability zero.

So I think it's correct to say "if I flip a coin long enough, at some point I'll get heads" even though we understand that "all tails forever" is one of the infinitely many possible sequences of coin flips.

[-]Primer2y10

I think that's what makes this a paradox.

[-]Wamba-Ivanhoe2y30

Going back to each of the finite cases, we can condition the finite case by the population that can support up to m rounds. iteration by the population size presupposes nothing about the game state and we can construct the Bayes Probability table for such games.

For a population that supports at most $m$ rounds of play the probability that a player will be in any given round $n <= m$ is $\frac{2^{n}}{M}$ and the sum of the probabilities that a player is in round n from $n = 1 \to m$ is $m \sum n = 1 \frac{2^{n - 1}}{M} = \frac{2^{m} - 1}{M}$ ; We can let $M = 2^{m} - 1$ because any additional population will not be sufficient to support an $m + 1$ round until the population reaches $2^{m + 1} - 1$ , which is just trading $m$ for $m + 1$ where we ultimately will take the limit anyhow.

The horizontal axis of the Bays Probability table now looks like this

$[\begin{matrix} \frac{1}{M} & \frac{2}{M} & \frac{4}{M} & \frac{8}{M} & . . . & \frac{2^{m - 1}}{M} \end{matrix}]$

The vertical axis of the Bays Probability table we can independently look at the odds the game ends at round n for n<=m. This can be due to snake eyes or it can be due to reaching round m with out rolling snake eyes. For the rounds $n = 1 \to m$ where snake eyes were rolled the probability of the game ending on round $n$ is $p * (1 - p)^{n - 1}$ and the probability that a reaches round $m$ with out ever rolling snake eyes is $(1 - p)^{m}$ . The sum of all of these possible end states in a game that has at most finite m rounds is $(1 - p)^{m} + \sum_{n = 1}^{m} p (1 - p)^{n - 1}$ which equals =1

So we have m+1 rows for the horizontal axis

$⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ \begin{matrix} p p (1 - p) p (1 - p)^{2} p (1 - p)^{3} ⋮ p (1 - p)^{m} (1 - p)^{m} \end{matrix} ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦$

So the Bayes Probability Table starts to look like this in general.

$⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ \begin{matrix} [\begin{matrix} \frac{1}{M} & \frac{2}{M} & \frac{4}{M} & \frac{8}{M} & . . . & \frac{2^{m - 1}}{M} \end{matrix}] ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ \begin{matrix} p p (1 - p) p (1 - p)^{2} p (1 - p)^{3} ⋮ p (1 - p)^{m} (1 - p)^{m} \end{matrix} ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ & ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ \begin{matrix} \frac{p}{M} & \frac{2 p}{M} & \frac{4 p}{M} & \frac{8 p}{M} & . . . & \frac{p * 2^{m - 1}}{M} \frac{p (1 - p)}{M} & \frac{2 p (1 - p)}{M} & \frac{4 p (1 - p)}{M} & \frac{8 p (1 - p)}{M} & . . . & \frac{p (1 - p) * 2^{m - 1}}{M} \frac{p (1 - p)^{2}}{M} & \frac{2 p (1 - p)^{2}}{M} & \frac{4 p (1 - p)^{2}}{M} & \frac{8 p (1 - p)^{2}}{M} & . . . & \frac{p (1 - p)^{2} * 2^{m - 1}}{M} \frac{p (1 - p)^{3}}{M} & \frac{2 p (1 - p)^{3}}{M} & \frac{4 p (1 - p)^{3}}{M} & \frac{8 p (1 - p)^{3}}{M} & . . . & \frac{p (1 - p)^{3} * 2^{m - 1}}{M} ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \frac{p (1 - p)^{m - 1}}{M} & \frac{2 p (1 - p)^{m - 1}}{M} & \frac{4 p (1 - p)^{m - 1}}{M} & \frac{8 p (1 - p)^{m - 1}}{M} & . . . & \frac{p (1 - p)^{m - 1} * 2^{m - 1}}{M} \frac{(1 - p)^{m}}{M} & \frac{2 (1 - p)^{m}}{M} & \frac{4 (1 - p)^{m}}{M} & \frac{8 (1 - p)^{m}}{M} & . . . & \frac{(1 - p)^{m} * 2^{m - 1}}{M} \end{matrix} ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ \end{matrix} ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦$

The total probability of losing is equal to the sum of the diagonal where i=j

$\frac{p}{M} + \frac{2 p (1 - p)}{M} + \frac{4 p (1 - p)^{2}}{M} + \frac{8 p (1 - p)^{3}}{M} + . . . + \frac{p (1 - p)^{m - 1} * 2^{m - 1}}{M} = \frac{p}{M} m \sum i = 1 [(1 - p)^{i - 1} * 2^{i - 1}]$

Total probability of being chosen is the sum of the diagonal and all the cells below the diagonal.

$m \sum i = 1 [\frac{2^{i - 1} * (1 - p)^{m}}{M}] + m \sum i = 1 i \sum j = 1 [\frac{2^{j - 1} * p (1 - p)^{i - 1}}{M}]$

$= \frac{(2^{m} - 1) (1 - p)^{m}}{M} + \frac{p}{M} m \sum i = 1 [(2^{i} - 1) (1 - p)^{i - 1}]$

So the conditional probability of losing given that you have been selected is

$\frac{\frac{p}{M} \sum_{i = 1}^{m} [(1 - p)^{i - 1} * 2^{i - 1}]}{\frac{(2^{m} - 1) (1 - p)^{m}}{M} + \frac{p}{M} \sum_{i = 1}^{m} [(2^{i} - 1) (1 - p)^{i - 1}]}$

$= \frac{p \sum_{i = 1}^{m} [(1 - p)^{i - 1} * 2^{i - 1}]}{(2^{m} - 1) (1 - p)^{m} + p \sum_{i = 1}^{m} [(2^{i} - 1) (1 - p)^{i - 1}]}$ $= p$

More over with the full Bayes Probability table we can find other conditional probabilities at infinity by taking the limit as the population grows to allow bigger and bigger maximum rounds of m.

So the conditional probability of losing given that you have been selected from an infinite population

Such as the conditional probability of being chosen in the game that has no snake eyes given you were chosen at all.

Or the conditional probability of dying given that you were chosen in precisely round k

[-]Primer2y20

This seems like great work! If we're allowing to run out of players, the whole paradox collapses.

[-]localdeity2y71

Because I'm not a real mathematician, I'm not going to find the actual limit, but just show that the limit is at least 50%.

Note that 1 + 2 + 4 + ... + 2^(n-1) = 2^n - 1. Therefore, if we have a bunch of blue-eyed groups of size 1, 2, 4, ..., 2^(n-1), and one red-eyed group of size 2^n, then the overall fraction of snakes that are red-eyed is 2^n / (2^n + 2^n - 1), which, if we divide the numerator and denominator by 2^n, comes out to 1 / (2 - 1/(2^n)). This is slightly above 1/2, and the limit as n -> ∞ is exactly 1/2.

[-]Martin Randall2y10

This is exactly right under SIA, thanks. Under SIA, almost all the snakes exist in the final scenario, and therefore the limit is 50% as n -> infinity.

Under SSA it's a bit higher than 50%, because we always have a 1/36 chance of there being a single red-eyed snake.

[-]N1X2y32

Right, and the correct value is 37/72, not 19/36, because exactly half of the remaining 70/72 players lose (in the limit).

[-]Dagon2y72

It would be useful to have a summary (at the top or bottom) that this post is mostly about comparing SSA and SIA, and readers familiar with the differences can skim most of it.

IMO, the key is to remember that probability is in the map (or the agent's head, if you prefer), not the territory. Unless you're talking about God (who famously doesn't play dice, but kind of seems to), all probabilities are 1 or 0 - that is the universe you're in, or it isn't. Your assignment of probability is based on your prediction of which universe you're in (ignoring logical uncertainty for this comment). Which means you really need to ask about what future experience OF THE AGENT is being predicted by the probability calculation of the agent.

From the experiment-runner's perspective, half of players die, and any given player AFTER the experiment, without knowing what group the player is in, has 50% chance of death. From a PLAYER's perspective, they have a 1/36 chance of death if the experiment is still open, and a 0% chance of death if it's finished and they're alive to answer the question.

[-]Martin Randall2y31

Interesting. Using the snake-creating deity setting, what should I expect as a newly created sightless snake, waiting for my eyes? Suppose that the deity will answer my questions while I wait for the dice roll.

SIA: I expect that the deity has created an indescribably large number of batches, and has not rolled snake eyes yet. I expect that there is a 1/36 chance that they will roll snake eyes this time. If they don't, they will likely roll up more batches, and those probabilities will be pretty normal. And then I'll end up on a indescribably large world with an indescribable number of snakes, of which 50% are red-eyed.

SSA: I expect that the deity has created several batches of snakes, within the expected bounds of a Poisson distribution with P=1/36. I expect that there is a 50% chance that they will roll snake eyes this time, because while the dice are fair, if the deity rolls snake eyes then I am about 35x more real. And then I'll end up on a large world with lots of snakes (eg, 2^36), of which just over 50% are red-eyed.

So under SIA the past is shaped by anthropics, and under SSA the future is shaped by anthropics. And whatever happens I get very compelling evidence on the SSA vs SIA question.

[-]avturchin2y30

Can we find real world situation which already happening and is similar to this game? In that case we can solve SIA vs SSA experimentally.

[-]Dagon2y30

If the deity is answering questions, you know it's before the roll, so it's clearly 1/36. The current size of the population (50% blue-eyed and 50% not-yet-determined) is irrelevant - this game has no upper bound, and past dice outcomes do not change the probability of future ones. This holds as well if you know that you're in the most recent batch.

The conundrum is if you are a snake whose age is unknown who just doesn't know their eye color yet. It's 100% blue if the game is ongoing, and 50% if the game is ended, so the question is "what is the probability that the game has ended". There's no uncertainty about that to the deity - they know whether the game is ongoing or ended. There is definitely uncertainty to the player, and it will be resolved when they discover their own eye color.

In this case, I support SSA and would wager 50%. Note that this is a pretty specific setup, and doesn't apply to even similar-sounding anthropic arguments.

[-]kwiat.dev2y52

I feel like this is one of the cases where you need to be very precise about your language, and be careful not to use an "analogous" problem which actually changes the situation.

Consider the first "bajillion dollars vs dying" variant. We know that right now, there's about 8B humans alive. What happens if the exponential increase exceed that number? We probably have to assume there's an infinite number of humans, fair enough.

What does it mean that "you've chosen to play"? This implies some intentionality, but due to the structure of the game, where the number of players is random, it's not really just up to you.

NOTE: I just realized that the original wording is "you're chosen to play" rather than "you've chosen to play". Damn you, English. I will keep the three variants below, but this means that the right interpretation clearly points towards option B), but the analysis of various interpretations can explain why we even see this as a paradox.

A) One interpretation is "what is the probability that I died given that I played the game?", to which the answer is 0%, because if I died, I wouldn't be around to ask this question.

B) Second interpretation is "Organizer told you there's a slot for you tomorrow in the next (or first) batch. What is the probability that you will die given that you are going to play the game?". Here the answer is pretty trivially 1/36. You don't need anthropics, counterfactual worlds, blue skies. You will roll a dice, and your survival will entirely depend on the outcome of that roll.

C) The potentially interesting interpretation, that I heard somewhere (possibly here) is: "You heard that your friend participated in this game. Given this information, what is the probability that your friend died during the game?". The probability here will be about 50% -- we know that if N people in total participated, about N/2 people will have died.

Consider now the second variant with snakes and colors. Before the god starts his wicked game, do snakes exist? Or is he creating the snakes as he goes? The first sentence "I am a god, creating snakes." seems to imply that this is the process of how all snakes are created. This is important, because it messes with some interpretations. Another complication is that now, "losing" the roll no longer deletes you from existence, which similarly changes interpretations. Let's look at the three variants again.

A) "What is the probability you have red eyes given that you were created in this process?" -- here the answer will be ~50%, following the same global population argument as in variant C of the first variant. This is the interpretation you seem to be going with in your analysis, which is notably different than the interpretation that seems to be valid in the first variant.

B) If snakes are being created as you go with the batches, this no longer has a meaning. The snake can't reflect on what will happen to him if he's chosen to be created, because he doesn't exist.

C) "Some time after this process, you befriended a snake who's always wearing shades. You find out how he was created. Given this, what is the probability that he has red eyes?" -- the answer, following again the same global population argument, is ~50%

In summary, we need to be careful switching to a "less violent" equivalent, because it can often entirely change the problem.

[-]Martin Randall2y22

I definitely agree on the need for care in switching between variants. It can also be helpful that they can "change the situation" because this can reveal something unspecified about the original variant. Certainly I was helped by making a second variant, as this clarified for me that the probabilities are different from the deity view vs the snake view, because of anthropics.

In the original variant, it's not specified when exactly players get devoured. Maybe it is instant. Maybe everyone is given a big box that contains either a bazillion dollars, or human-eating snakes, and it opens exactly a year later.

In my variant, I was imagining the god initially created a batch of snakes with uncolored eyes, then played dice, then gave them red or blue eyes. So the snakes, like the players, can have experiences prior to the dice being rolled. And yes, no snakes exist before I start. (why is the god wicked? No love for snakes...) I'll update the text to clarify that no snakes exist until the god of snake creation gets to work.

C) "Some time after this process, you befriended a snake who's always wearing shades. You find out how he was created. Given this, what is the probability that he has red eyes?" -- the answer, following again the same global population argument, is ~50%

I think this is a great crystallization of the paradox. In this scenario, it seems like I should believe I have a 1/36 chance of red eyes, and my new friend has a 1/2 chance of red eyes. But my friend has had exactly the same experiences as me, and they reason that the probabilities are reversed.

[-]avturchin2y41

Is it epistemically isomorphic to sleeping beuaty problem?

[-]Martin Randall2y41

The SSA vs SIA debate impacts both questions, but once you pick one of those then in Sleeping Beauty there's a clear answer of 1/2 or 1/3, whereas in this problem the infinities continue to make it unclear what the probability should be.

[-]Tapatakt2y40

It depends.

If croupier choose the players, then players learn that they were chosen, then croupier roll the dice, then players either get bajillion dollars each or die, then (if not snake eyes) croupier choose next players and so on - answer is 1/36.

If croupier choose the players, then roll the dice, then (if not snake eyes) croupier choose next players and so on, and only when dice come up snake eyes players learn that they were chosen, and then last players die and all other players get bajillion dollars each - answer is about 1/2.

[-]Chris_Leong2y*31

(I'll probably post an expanded/edited version as a full-post soon, just wanted to see what I could produce in a single sitting. Apologies, as I engage in some handwaving).

I think it's worth breaking this down more.

In scenario 1, you learn that you are a participant who was selected in round r, where r is unknown.

In scenario 2, you learn that you are a participant who was selected full-stop.

If this was all you learned, then these two scenarios would be equivalent, as all selected participants were selected in some round.

However, I'll argue in the next section that each scenario contains additional information about which round you should expect to be in.

Analysing Indexical Information

In scenario 1, the participants are informed at different times depending on their group.

When a participant is informed they were selected, they know:

a) that the previous rounds were already rejected and

b) that if they aren't eliminated, then additional rounds will be run, but you aren't in those future run

c) that the dice are about to be thrown for them

In scenario 2, all selected participants are informed at once. Participants still know:

a) that all rounds before them were rejected AND

b) if they weren't marked to be eliminated, then additional rounds were run

c) that the dice were thrown for them

Again, aren't these the same?

In the next section, I'll argue that the exact mechanism of how and when people are informed affects the way that we handle reference classes.

Analysing Reference Classes

Reference classes are strange. It's not clear what we mean by reference classes.

Should it be the people in the same round as us, or everyone who ends up in the snake eyes problem?

One answer would be that in both scenarios it should be everyone who ends up in the same problem, such that the reference classes are the same (following the argument that you have no non-anthropic information about which round you are it)

Another answer would be that in scenario 1, your reference class is everyone in the same round due to indexical information, but in scenario 2, it is everyone in the problem due to the lack of such information.

So how should we interpret the indexical information when figuring out your reference class?

First, let's imagine that we've fixed round r. In that case, it's obvious that your reference class is everyone in this round and that everyone in the round has a 1/36 chance of being eliminated regardless of who they are.

We then want to consider the case where you don't know which round you are in. This requires us to assign a probability distribution to rounds.

We can choose to start simple again and assume that there are n rounds in total. We now have to choose whether to say that your chance of being in any particular round is 1/n or whether it is proportional to the number of people in that round?

I'm going to suggest that the indexical information (that previous rounds have passed and future rounds are yet to come) tells you that it should be the former. There's a sense in which people with the same indexical information naturally belong in the same group and it would be weird to mix them all together as per the proportional case. This is somewhat handwavey, but hopefully, I can make a more rigorous argument in future work.

This leads to your chance of being in any particular round is 1/n. Again, since all rounds have the same probability of being eliminated, this doesn't affect anything.

We can then extend to the case where we don't know the number of rounds. With snake eyes, there's a 1/36*(35/36)^(i-1) chance that it goes for i rounds. Again, there's the question of weighting by pure probability of the game lasting that long or to also take into account the number of rounds. Luckily, we don't have to decide as the probability of each of the cases we are weighting is 1/36, giving 1/36 overall.

In scenario 2, all selected participants are informed at once, so they don't have access to the same indexical information, although they do have indexical information about all rounds having been run (essentially fixes n, even though this is unknown).

If we also fix the number of players as x, then your chance of being in round r with 2^(r-1) participants is 2^(r-1)/x, as you lack any information about which round you were in beyond the anthropic bias of being more likely to be in a larger round.

We can then aggregate over all possible n.

Again, there's the question of whether we should weight purely by probabilities or take into account the number of people in each scenario. And again, I'm tempted to say that the indexical information indicates that we should treat a fixed n as a single group, and so weight purely by probabilities.

However, regardless, we can observe that we always have > 50% chance of being in the last round, so there's > 50% chance of being in the last round overall.

Thoughts on aggregation:

I'm still confused here, but there seem to be two kinds of aggregation:

One where we group everything into one scenario
One where imagine ourselves to have a group of different scenarios

I don't know what the difference is yet.

[-]Chris_Leong2y40

I’m already wanting to update my analysis.

Informing everyone together means that they should be treated as one group regardless of what round they were in.

Informing one round at a time means dealing with anthropics.

[-]Chris_Leong2y30

Let’s consider a scenario where we skip the doubling. So, we have a long line of people, people play one at a time, 50% chance they win a prize, 50% they are eliminated, game ends after first elimination.

It’s quite clear that in expectation, more than 50% of people who played lose the game even though it’s a fair coin (we have a 50% chance of 100% of players losing). This will be explained momentarily.

Imagine the players as a team who score 1 point when they win and lose 1 point when eliminated, with the ability to stop at any time, but who have adopted this stopping strategy.

This strategy of stopping means you come out behind with 50% chance, even with 25% chance and ahead with 25% chance.

If we now look at the percent of wins vs. losses, we can see that we expect more losses than wins on average (though the calculation is more complicated).

The point is that you should only expect an average of half the coin flips to be heads when you adopt some kind of uniform stopping rule, such as always stopping after N rounds. Otherwise, you can pick a stopping rule that makes these kinds of trade-offs.

So you are more likely to lose than win. However, it allows you to maintain uncapped potential profit, whilst your losses are capped at 1.

We can note consider snake eyes from a team perspective. It’s similar, but more extreme. This time your team almost guaranteed to lose one point, though there is an infinitesimal chance that you score infinite points.

This sounds like free money from the perspective of the house, but it’s not, it’s just a martingale.

[-]Wamba-Ivanhoe2y*30

Because all scenarios have P(red) >= 50%, the combined P(red) >= 50%. This holds for both SIA and SSA.

The statement above is only true if the stopping condition is that "If we get to the batch we will not roll dice but instead only make snakes with red eyes", or in other words $B$ must have been selected because it resulted in red eyes.

Where $B$ is selected as the stopping condition independent of the dice result, the fate of batch $B$ is still a dice roll so there exists a $B + 1$ scenario. Any scenario stopping less than $B$ must have stopped because snakes with red eyes were made, however batch $B$ could result either in $2^{B - 1}$ snakes with red eyes with probability $d = 1 / 36$ or $2^{B - 1}$ snakes with blue eyes with probability $(1 - d) = 35 / 36$ . The fact that snakes are more likely to be blue eyed in batch $B$ than they are to be red combined with the exponential weight of batch $B$ is not with out consequence.

Note that sequence of weights provided the table are the summation terms required to find expected number of snakes created. A sum product of the series of the number of players in each scenario { 1, 3, 7, ... , $2^{n} - 1$ } and the frequency of terminating at a given scenario due to death { $d (1 - d)^{i - 1}$ } for $i = 1 \to n$ . Note: however that the sum of the scenario frequencies is $d \times \sum_{i = 1}^{n} (1 - d)^{i - 1} = 1 - (1 - d)^{n}$ . This sum is less than $1$ , so we need to recover the missing $(1 - d)^{n}$ probability which comes from the scenario where all snakes have blue eyes, our $B + 1$ scenario/term required to find the expected number of snakes.

[-]Martin Randall2y10

Are all snakes equally real (in proportion to their likelihood of existing)? I'm assuming yes in the post, but that leads to weirdness like undefined probabilities, which we'd prefer to avoid. Also, because there are infinite snakes, there would be a zero probability of being any particular snake, or (under SIA) being in any particular batch of snakes.

If we distribute realityfluid to the snakes in differing amounts, to avoid that, then we can probably avoid the undefined probabilities. The probability of having red eyes will depend on the formula for distributing realityfluid. Then instead of saying "the probability is undefined" we can say "the probability depends on this undefined formula".

[-]Noosphere892y22

Also, because there are infinite snakes, there would be a zero probability of being any particular snake, or (under SIA) being in any particular batch of snakes.

Hot take, but this is actually a valid answer, and in infinite sets/infinite outcome spaces this can actually start mattering.

The classic example is if you pick a number from the number line at random, you will have a 0% chance of picking a rational number, or any number that isn't a real number.

This article	Reeves	Leslie's Shooting Room
Soul	Person not (yet) picked	Person not (yet) picked
Eyeless snake	Person in game	Person in room
Red-eyed snake	Person about to be devoured by snakes	Person about to be shot
Blue-eyed snake	Person about to get a bazillion dollars	Person about to leave room alive

LESSWRONG
LW

LESSWRONG
LW

22

22

22

Calculating the odds of dying when playing the snake-eyes game with a player base of arbitrary size.

Problem statement

Less death please

Anthropic Probability

Self-sampling assumption

What is it like to live in an SSA world?

Self-indication assumption

What is it like to live in an SIA world?

Trying to find a limit for SIA

Conditional on the game stopping by batch B

Can we take the limit?

Purple-eyed snakes

Conclusion

Resolution of a Manifold Market

References

N	Weight
1	d
2	3d(1-d)
3	7d(1-d)²