Alternative Models of Superposition
12StefanHex
8Alex Gibson
1zroe1
1Alex Gibson
1zroe1
3Jon Garcia
New Comment
Reposting my Slack comment here for the record: I'm excited to see challenges to our fundamental assumptions and exploration of alternatives!
Unfortunately, I think that the modified loss function makes the task a lot easier, and the results not applicable to superposition. (I think @Alex Gibson makes a similar point above.)
In this post, we use a loss function that focuses only on reconstructing active features
It is much easier to reconstruct the active feature without regard for interference (inactive features also appearing active).
In general, I find that the issue in NNs is that you not only need to "store" things in superposition, but be able to read them off with low error / interference. Chris Olah's note on "linear readability" here (inspired by the Computation in Superposition work) describes that somewhat.
We've experimented with similar loss function ideas (almost the same as your loss actually, for APD) at Apollo, but always found that ignoring inactive features makes the task unrealistically easy.
The restriction of the loss to the target feels like cheating, to be honest. The linear model claim is scoped to reconstruction loss, where you genuinely don't see superposition as far as i'm aware. And in this case, the reconstruction loss would be poor, because the vectors are nested so close to each other that adjacent features false fire.
I agree with the core point about finding alternative models of superposition though. As far as I know, there is no evidence that the Toy Model paper is accurate to how real models actually represent things, except at the broadest level. Towards Monosemanticity in fact notes divergence from the Toy Model paper (see Feature Splitting).
On the model itself, for , and , why can't you place vectors equidistant around the circle, allowing for arbitrarily many features?
To your point about the loss, I believe it's absolutely correct that this is an entirely different setting than the linear models from TMS. I wouldn't characterize this as cheating, because it feels entirely possible that models in practice have an effective mechanism for handling lots of interference, but admittedly, the fact that you only select the target feature is the difference that makes this experiment work at all.
On the model itself, for , and , why can't you place vectors equidistant around the circle, allowing for arbitrarily many features?
If I understand this question correctly, for it should be possible to have arbitrarily many features. In this setting, there is no possibility for interference so if you tune hyperparameters correctly, you should be able to get as many features as you want. Empirically, I didn't find a clear limit but, at the very least I can say that you should be able to get "a lot." Because all inputs are orthogonal, in this case, the results should be very similar to Superposition, Memorization, and Double Descent.
would be an interesting experiment that I didn't run, but if I had to guess, the results wouldn't be very clean because there would be quite a bit of interference on each training example.
I guess I mean cheating purely as "I don't think this applies to to the Toy Model setting", as opposed to saying it's not a potentially valuable loss to study.
For p=1.0, I forgot that each of the noise features are random between 0 and 0.1, as opposed to fixed magnitude. The reason I brought it up is because if they were fixed magnitude 0.05 then they would all cancel out and face in the opposite direction to the target feature with magnitude 0.05. Now I reread the setting again I don't think that's relevant, though.
The reason I brought it up is because if they were fixed magnitude 0.05 then they would all cancel out and face in the opposite direction to the target feature with magnitude 0.05. Now i'm curious what the variance in noise looks like as a function of number of features if you place them equidistant.
This is a very interesting thought! I think your intuition is probably correct even though it is somewhat counterintuitive. Perhaps I'll run this experiment at some point.
This seems deeply connected to Modern Hopfield Networks, which have been able to achieve exponential memory capacity relative to the number of dimensions, compared to the linear memory capacity of traditional Hopfield networks. The key is the use of the softmax nonlinearity between the similarity and projection steps of the memory retrieval mechanism, which seems like an obvious extension of the original model in hindsight. Apparently, there is a lot of mathematical similarity between these memory models and the self-attention layers used in Transformers.
What you're looking at is also closely related to the near-orthogonality property of random vectors in high-dimensional space, which is a key principle behind hyperdimensional computing / vector-symbolic architectures. So-called hypervectors (which may be binary, bimodal, real-valued, complex-valued, etc.) can be combined via superposition, binding, and permutation operations into interpretable data structures in the same high-dimensional space as the elemental hypervectors. The ability to combine into and extract from superposition is key to the performance of these models.
As dimensionality of your space increases, the standard deviation of the distribution of inner products of pairs of unit vectors sampled uniformly from this space falls off as :
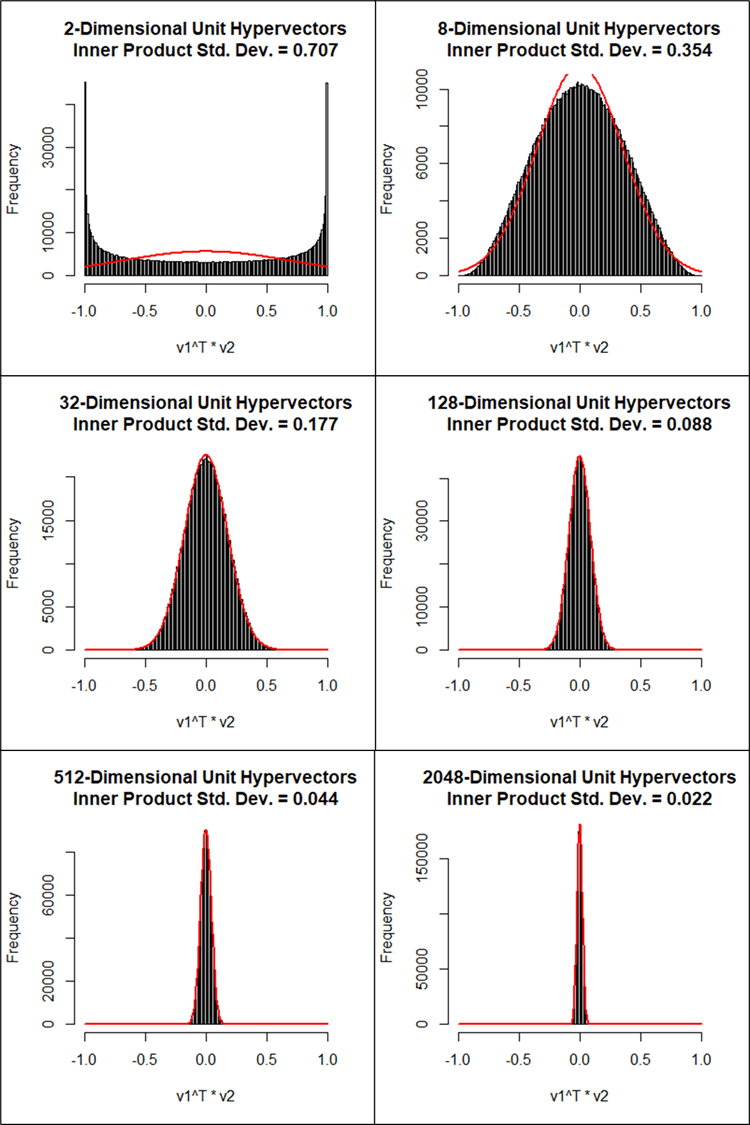
In other words, for any given threshold of "near-orthogonality", the probability that any two randomly sampled (hyper)vectors will have an inner product with an absolute value smaller than this threshold grows to near-certainty with a high enough number of dimensions. A 1000-dimensional space effectively becomes a million-dimensional space in terms of the number of basis vectors you can combine in superposition and still be able to tease them apart.