To illustrate what I mean, switching from p(doom) to timelines: 

• The recent post AGI Timelines in Governance: Different Strategies for Different Timeframes was useful to me in pushing back against Miles Brundage's argument that "timeline discourse might be overrated", by showing how choice of actions (in particular in the AI governance context) really does depend on whether we think that AGI will be developed in ~5-10 years or after that. 
• A separate takeaway of mine is that decision-relevant estimation "granularity" need not be that fine-grained, and in fact is not relevant beyond simply "before or after ~2030" (again in the AI governance context). 
• Finally, that post was useful to me in simply concretely specifying which actions are influenced by timelines estimates.  

Question: Is there something like this for p(doom) estimates? More specifically, following the above points as pushback against the strawman(?) that "p(doom) discourse, including rigorous modeling of it, is overrated":

1. What concrete high-level actions do most alignment researchers agree are influenced by p(doom) estimates, and would benefit from more rigorous modeling (vs just best guesses, even by top researchers e.g. Paul Christiano's views)?
2. What's the right level of granularity for estimating p(doom) from a decision-relevant perspective? Is it just a single bit ("below or above some threshold X%") like estimating timelines for AI governance strategy, or OOM (e.g. 0.1% vs 1% vs 10% vs >50%), or something else?
   • I suppose the easy answer is "the granularity depends on who's deciding, what decisions need making, in what contexts", but I'm in the dark as to concrete examples of those parameters (granularity i.e. thresholds, contexts, key actors, decisions)
   • e.g. reading Joe Carlsmith's personal update from ~5% to >10% I'm unsure if this changes his recommendations at all, or even his conclusion – he writes that "my main point here, though, isn't the specific numbers... [but rather that] here is a disturbingly substantive risk that we (or our children) live to see humanity as a whole permanently and involuntarily disempowered by AI systems we’ve lost control over", which would've been true for both 5% and 10%

Or is this whole line of questioning simply misguided or irrelevant? 

Some writings I've seen gesturing in this direction:

• harsimony's argument that Precise P(doom) isn't very important for prioritization or strategy ("identifying exactly where P(doom) lies in the 1%-99% range doesn't change priorities much") amounts to the 'single bit granularity' answer
  • Carl Shulman disagrees, but his comment (while answering my 1st bullet point) isn't clear in the way the different AI gov strategies for different timelines post is, so I'm still left in the dark – to (simplistically) illustrate with a randomly-chosen example from his reply and making up numbers, I'm looking for statements like "p(doom) < 2% implies we should race for AGI with less concern about catastrophic unintended AI action, p(doom) > 10% implies we definitely shouldn't, and p(doom) between 2-10% implies reserving this option for last-ditch attempts", which he doesn't provide
• Froolow's attempted dissolution of AI risk (which takes Joe Carlsmith's model and adds parameter uncertainty – inspired by Sandberg et al's Dissolving the Fermi paradox – to argue that low-risk worlds are more likely than non-systematised intuition alone would suggest) 
  • Froolow's modeling is useful to me for making concrete recommendations for funders, e.g. (1) "prepare at least 2 strategies for the possibility that we live in one of a high-risk or low-risk world instead of preparing for a middling-ish risk", (2) "devote significantly more resources to identifying whether we live in a high-risk or low-risk world", (3) "reallocate resources away from macro-level questions like 'What is the overall risk of AI catastrophe?' towards AI risk microdynamics like 'What is the probability that humanity could stop an AI with access to nontrivial resources from taking over the world?'", (4) "When funding outreach / explanations of AI Risk, it seems likely it would be more convincing to focus on why this step would be hard than to focus on e.g. the probability that AI will be invented this century (which mostly Non-Experts don’t disagree with)". I haven't really seen any other p(doom) model do this, which I find confusing 
• I'm encouraged by the long-term vision of the MTAIR project "to convert our hypothesis map into a quantitative model that can be used to calculate decision-relevant probability estimates", so I suppose another easy answer to my question is  just "wait for MTAIR", but I'm wondering if there's a more useful answer to the "current SOTA" than this. To illustrate, here's (a notional version of) how MTAIR can help with decision analysis, cribbed from that introduction post: 

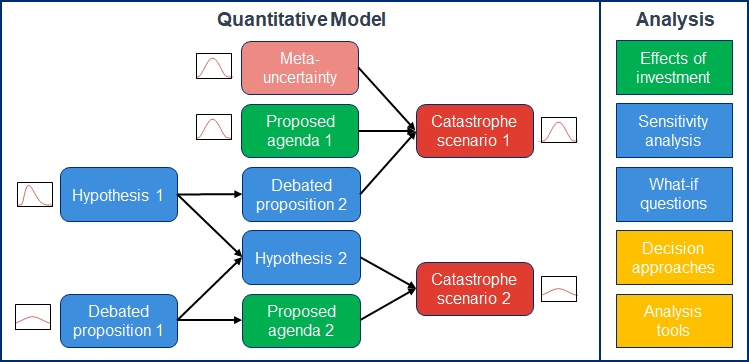
This question was mainly motivated by my attempt to figure out what to make of people's widely-varying p(doom) estimates, e.g. in the appendix section of Apart Research's website, beyond simply "there is no consensus on p(doom)". I suppose one can argue that rigorous p(doom) modeling helps reduce disagreement on intuition-driven estimates by clarifying cruxes or deconfusing concepts, thereby improving confidence and coordination on what to do, but in practice I'm unsure if this is the case (reading e.g. the public discussion around the p(doom) modeling by Carlsmith, Froolow, etc), so I'm not sure I buy this argument, hence my asking for concrete examples.