This is crossposted from my new blog, following up on my previous post. It introduces the original "Newcomb's problem" and discusses the motivation behind twoboxing and the reasons why CDT fails. content is probably review for most LessWrongers, later posts in the sequence may be of more interest.

---

Last time I introduced causal decision theory (CDT) and showed how it has unsatisfactory behavior on "Newcomblike problems". Today, we'll explore Newcomblike problems in a bit more depth, starting with William Newcomb's original problem.

The Problem

Once upon a time there was a strange alien named Ω who is very very good at predicting humans. There is this one game that Ω likes to play with humans, and Ω has played it thousands of times without ever making a mistake. The game works as follows:

First, Ω observes the human for a while and collects lots of information about the human. Then, Ω makes a decision based on how Ω predicts the human will react in the upcoming game. Finally, Ω presents the human with two boxes.

The first box is blue, transparent, and contains $1000. The second box is red and opaque.

You may take either the red box alone, or both boxes,

Ω informs the human. (These are magical boxes where if you decide to take only the red one then the blue one, and the $1000 within, will disappear.)

If I predicted that you would take only the red box, then I filled it with $1,000,000. Otherwise, I left it empty. I have already made my choice,

Ω concludes, before turning around and walking away.

You may take either only the red box, or both boxes. (If you try something clever, like taking the red box while a friend takes a blue box, then the red box is filled with hornets. Lots and lots of hornets.) What do you do?

The Dilemma

Should you take one box or two boxes?

If you take only the red box, then you're necessarily leaving $1,000 on the table.

But if you take both boxes, then Ω predicted that, and you miss out at a chance of $1,000,000.

Recap

Now, as you'll remember, we're discussing decision theories, algorithms that prescribe actions in games like these. Our motivation for studying decision theories is manyfold. For one thing, people who don't have tools for making good decisions can often become confused (remember the people who got palm surgery to change their fortunes).

This is not just a problem for irrational or undereducated people: it's easy to trust yourself to make the right choices most of the time, because human heuristics and intuitions are usually pretty good. But what happens in the strange edge-case scenarios? What do you do when you encounter problems where your intuitions conflict? In these cases, it's important to know what it means to make a good choice.

My motivation for studying decision theory is that in order to construct an artificial intelligence you need a pretty dang good understanding of what sort of decision algorithms perform well.

Last post, we explored the standard decision theory used by modern philosophers to encode rational decision making. I'm eventually going to use this series of posts to explain why our current knowledge of decision theory (and CDT in particular) are completely inadequate for use in any sufficiently intelligent self-modifying agent.

But before we go there, let's see how causal decision theory reacts to Newcomb's problem.

The Choice

Let's analyze this problem using causal decision theory from yesterday. Roughly, the causal decision theorist reasons as follows:

Ω offers me the boxes after making its decision. Now, either Ω has filled the red box or Ω has not filled the red box. The decision has already been made. If Ω filled the red box, then I had better take both boxes (and get a thousand and a million dollars). If Ω didn't fill the red box, then I had better take both boxes so that I at least get a thousand dollars. No matter what Ω chose, I had better take both boxes.

And so, someone reasoning using causal decision theory takes both boxes (and, because Ω is a very good predictor, they walk away with $1000).

Let's walk through that reasoning in slow-mo, using causal graphs. The causal graph for this problem looks like this:

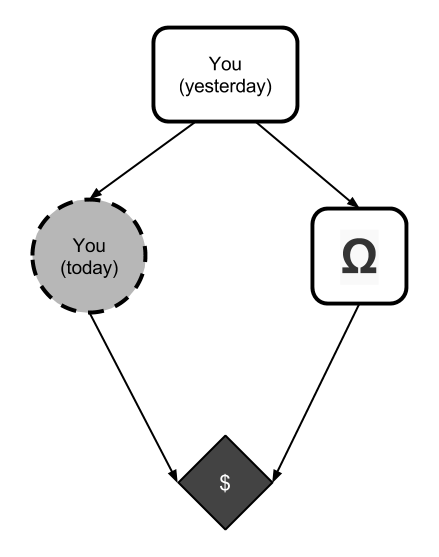
With the nodes defined as follows:

• You (yesterday) is the algorithm implementing you yesterday. In this simplified setting, we assuem that its value determines the contents of You (today).
• Ω is a function that observes you yesterday and decides whether to put $1,000,000 into the red box. Its value is either filled or empty.
• You (today) is your decision algorithm. It must output either onebox or twobox.
• $ is $1,000,000 if Ω=filled plus $1,000 if You (today)=twobox.

We must decide whether to output onebox (take only the red box) or twobox (take both boxes). Given some expecation p that Ω=filled, causal decision theory reasons as follows:

1. The decision node is You (today).
2. The available actions are onebox and twobox.
3. The utility node is $.
4. Set You (today)=const onebox
   • $ = 1,000,000p
5. Set You (today)=const twobox
   • $ = 1,000,000p + 1,000

Thus, no matter what probability p is, CDT takes both boxes, because the action twobox results in an extra $1000.

The Excuse

This is, of course, the wrong answer.

Because Ω is a really good predictor, and because Ω only gives a million dollars to people who take one box, if you want a million dollars then you had better only take one box.

Where did CDT go wrong?

Causal decision theorists sometimes argue that nothing went wrong. It is "rational" to take both boxes, because otherwise you're leaving $1,000 on the table. Reasoning about how you have to take one box so that that box will be filled is nonsense, because by the time you're making your decision, Ω has already left. (This argument can be found at Foundations of Causal Decision Theory, p152.)

Of course, these people will agree that the causal decision theorists walk away with less money. But they'll tell you that this is not their fault: they are making the "rational" choice, and Ω has decided to punish people who are acting "rationally".

The Counter

There is some merit to this complaint. No matter how you make decisions, there is at least one decision problem where you do poorly and everybody else does well. To illustrate, consider the following game: every player submits a computer program that has to choose whether to press the green button or the blue button (by outputting either green or blue). Then I check which button your program is going to press. Then I give $10 to everyone whose program presses the opposite button.

Clearly, many people can win $10 in this game. Also clearly, you cannot. In this game, no matter how you choose, you lose. I'm punishing your decision algorithm specifically.

I'm sympathetic to the claim that there are games where the host punishes you unfairly. However, Newcomb's problem is not unfair in this sense.

Ω is not punishing people who act like you, Ω is punishing people who take two boxes. (Well, I mean, Ω is giving $1,000 to those people, but Ω is withholding $1,000,000 that it gives to oneboxers, so I'll keep calling it "punishment").

You can't win at the bluegreen game above. You can win on Newcomb's problem. All you have to do is only take one box.

Causal decision theorists claim that it's not rational to take one box, because that leaves $1,000 on the table even though your choice can no longer affect the outcome. They claim that Ω is punishing people who act reasonably. They can't just decide to stop being reasonable just because Ω is rewarding unreasonable behavior in this case.

To which I say: fine. But pretend I wasn't motivated by adherence to some archaic definition of "reasonableness" which clearly fails systematically in this scenario, but that I was instead motivated by a desire to succeed. Then how should I make decisions? Because in these scenarios, I clearly should not use causal decision theory.

The Failure

In fact, I can go further. I can point to the place where CDT goes wrong. CDT goes wrong when it reasons about the outcome of its action "no matter what the probability p that Ω fills the box".

Ω's choice to fill the box depends upon your decision algorithm.

If your algorithm chooses to take one box, then the probability that Ω=filled is high. If your algorithm chooses to take two boxes, then the probability that Ω=filled is low.

CDT's reasoning neglects this fact, because Ω is causally disconnected from You (today). CDT reasons that its choice can no longer affect Ω, but then mistakenly assumes that this means the probability of Ω=filled is independent from You (today).

Ω makes its decision based on knowledge of what the algorithm inside You (today) looks like. When CDT reasons about what would happen if it took one box, it considers what the world would look like if (counterfactually) You (today) was filled with an algorithm that, instead of being CDT, always returned onebox. CDT changes the contents of You (today) and nothing else, and sees what would happen. But this is a bad counterfactual! If, instead of implementing CDT, you implemented an algorithm that always took one box, then Ω would act differently.

CDT assumes it can change You (today) without affecting Ω. But because Ω's choice depends upon the contents of You (today), CDT's method of constructing counterfactuals destroys some of the structure of the scenario (namely, the connection between Ω's choice and your algorithm).

In fact, take a look at the graph for Newcomb's problem and compare it to the graph for the Mirror Token Trade from last post:

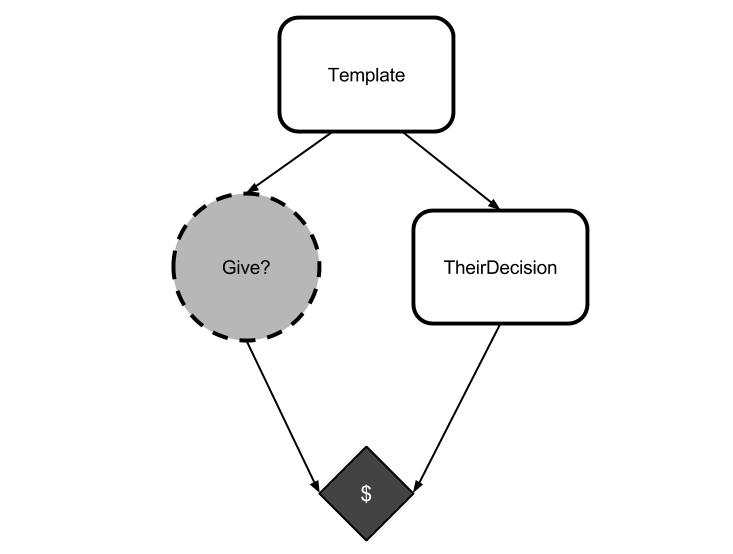
These are the same graph, and CDT is making the same error. It's assuming that everything which is causally disconnected from it is independent of it.

In both Newcomb's original problem and in the Mirror Token Trade, this assumption is violated. Ω's choice is logically connected to your choice, even though your choice is causally disconnected from Omega's.

In any scenario where there are logical non-causal connections between your action node and other nodes, CDT's method of counterfactual reasoning can fail.

The Solution

The solution, of course, is to respect the logical connection between Ω's choice and your own. I would take one box, because in this game, Ω gives $1,000,000 to people who use the strategy "take one box" and $1,000 to people who use the strategy "take two boxes".

There are numerous intuition pumps by which you can arrive at this solution. For example, you could notice that you would like to precommit now to take only one box, and then "implement" that precommitment (by becoming, now, the type of person who only takes one box).

Alternatively, you can imagine that Ω gets its impeccable predictions by simulating people. Then, when you find yourself facing down Ω, you can't be sure whether you're in the simulation or reality.

It doesn't matter which intuition pump you use. It matters which choice you take: and CDT takes the wrong one.

We do, in fact, have alternative decision theories that perform well in Newcomb's problem (some better than others), but we'll get to that later. For now, we're going to keep exaimining CDT.

Why I care

Both the Mirror Token Trade and Newcomb's Problem share a similar structure: there is another agent in the environment that knows how you reason.

We can generalize this to a whole class of problems, known as "Newcomblike problems".

In the Mirror Token Trade, the other agent is a copy of you who acts the same way you do. If you ever find yourself playing a token trade against a copy of yourself, you had better trade your token, even if you're completely selfish.

In Newcomb's original problem, Ω knows how you act, and uses this to decide whether or not to give you a million dollars. If you want the million, you had better take one box.

These problems may seem like weird edge cases. After all, in the Mirror Token Trade we assume that you are perfectly deterministic and that you can be copied. And in Newcomb's problem, we presume the existence of a powerful alien capable of perfectly predicting your action.

It's a chaotic world, and perfect prediction of a human is somewhere between "pretty dang hard" and "downright impossible".

So fine: CDT fails systematically on Newcomblike problems. But is that so bad? We're pretty unlikely to meet Ω anytime soon. Failure on Newcomblike problems may be a flaw, but if CDT works everywhere except on crazy scenarios like Newcomb's problem then it's hardly a fatal flaw.

But while these two example problems are simple scenarios where the other agents are "perfect" copies or "perfect" predictors, there are many more feasible Newcomblike scenarios.

Any scenario where another agent has knowledge about your decision algorithm (even if that knowledge is imperfect, even if they lack the capability to simulate you) is a Newcomblike problem.

In fact, in the next post (seriously, I'm going to get to my original point soon, I promise) I'll argue that Newcomblike problems are the norm.