(Cross-posted from my blog.) 

Confidence level: medium

I want to argue that Newcomb’s problem does not reveal any deep flaw in standard decision theory. There is no need to develop new decision theories to understand the problem.

I’ll explain Newcomb’s problem and expand on these points below, but here’s the punchline up front.

TLDR:

1. Newcomb’s problem, framed properly, simply highlights the issue of time consistency. If you can, you would beforehand commit to being the type of person who takes 1 box; but in the moment, under discretion, you want to 2-box.
2. That is: the answer to Newcomb depends on from which point in time the question is being asked. There’s just no right way to answer the question without specifying this.
3. Confusion about Newcomb’s problem comes when people describing the problem implicitly and accidentally conflate the two different possible temporal perspectives.
4. Newcomb’s problem is isomorphic to the classic time consistency problem in monetary policy – a problem that is well-understood and which absolutely can be formally analyzed via standard decision theory.

I emphasize that the textbook version of expected utility theory lets us see all this! There’s no need to develop new decision theories. Time consistency is an important but also well-known feature of bog-standard theory.
 

I. Background on Newcomb

(You can skip this section if you’re already familiar.)

Newcomb’s problem is a favorite thought experiment for philosophers of a certain bent and for philosophically-inclined decision theorists (hi). The problem is the following:

• Scientists have designed a machine for predicting human decisions: it scans your brain, and predicts on average with very high accuracy your choice in the following problem.
• I come to you with two different boxes:
  • 1. In one box, I show you there is $100.
  • 2. The second box is a mystery box.
• I offer to let you choose between taking just the one mystery box, or taking both the mystery box and the $100 box.
• Here’s the trick: I tell you that the mystery box either contains nothing or it contains a million dollars.
  • If the machine had predicted in advance that you would only take the mystery box, then I had put a million bucks in the mystery box.
  • But if the machine had predicted you would take both boxes, I had put zero in the mystery box.

As Robert Nozick famously put it, “To almost everyone, it is perfectly clear and obvious what should be done. The difficulty is that these people seem to divide almost evenly on the problem, with large numbers thinking that the opposing half is just being silly.”

The argument for taking both boxes goes like, ‘If there’s a million dollars already in the mystery box, well then I’m better off taking both and getting a million plus a hundred. If there’s nothing in the mystery box, I’m better off taking both and at least getting the hundred bucks. So either way I’m better off taking both boxes!’

The argument for “one-boxing” – taking only the one mystery box – goes like, ‘If I only take the mystery box, the prediction machine forecasted I would do this, and so I’ll almost certainly get the million dollars. So I should only take the mystery box!’
 

II. The critique of expected utility theory

It’s often argued that standard decision theory would have you “two-box”, but that since ‘you win more’ by one-boxing, we ought to develop a new form of decision theory (EDT/UDT/TDT/LDT/FDT/...) that prescribes you should one-box.

My claim is essentially: Newcomb’s problem needs to be specified more precisely, and once done so, standard decision theory correctly implies you could one- or two-box, depending on from which point in time the question is being asked.

III. Newcomb’s problem as a static problem

In the very moment that I have come to you, here is what your payoff table looks like:

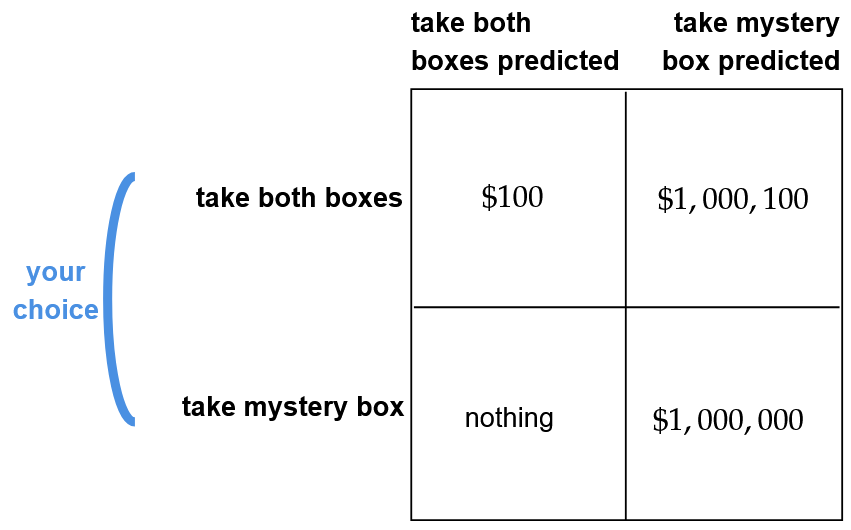
You are choosing between the first row and the second row; I’m choosing between the first column and the second column. Notice that if I’ve chosen the first column, you’re better off in the first row; and if I’ve chosen the second column, you’re also better off in the first row. Thus the argument for being in the first row – taking both boxes.

In the very moment that I have come to you, you ARE better off in taking both boxes.

To borrow a trick from Sean Carroll, go to the atomic level: in the very moment I have come to you, the atoms in the mystery box cannot change. Your choice cannot alter the composition of atoms in the box – so you ARE better off “two-boxing” and taking both boxes, since nothing you can do can affect the atoms in the mystery box.

I want to emphasize this is a thought experiment. You need to be sure to decouple your thinking here from possible intuitions that could absolutely make sense in reality but which we need to turn off for the thought experiment. You should envision in your mind’s eye that you have been teleported to some separate plane from reality, floating above the clouds, where your choice is a one-time action, never to be repeated, with no implications for future choices. (Yes, this is hard. Do it anyway!) If you one-box in the very moment, in this hypothetical plane separate from reality where this is a one-time action with no future implications, you are losing – not winning. You are throwing away utils.

IV. Newcomb’s problem as a dynamic problem

But what if this were a dynamic game instead, and you were able to commit beforehand to a choice? Here’s the dynamic game in extensive form:

Here I’ve presented the problem from a different moment in time. Instead of being in the very moment of choice, we’re considering the problem from an ex ante perspective: the time before the game itself.

Your choice now is not simply whether to one-box or to two-box – you can choose to commit to an action before the game. You can either:

1. Tie your hands and commit to only take one box. In which case the prediction machine would know this, predict your choice, I would put $1M in the mystery box, and so you would get $1M.
2. Don’t commit to anything. In which case you end up back in the same situation as the game table before, in the very moment of choice.

But we both already know that if you take the second option and don’t commit, then in the very moment of choice you’re going to want to two-box. In which case the machine is going to predict this, and I’m going to put nothing in the mystery box, so when you inevitably two-box after not committing you’ll only get the $100.

So the dynamic game can be written simply as:

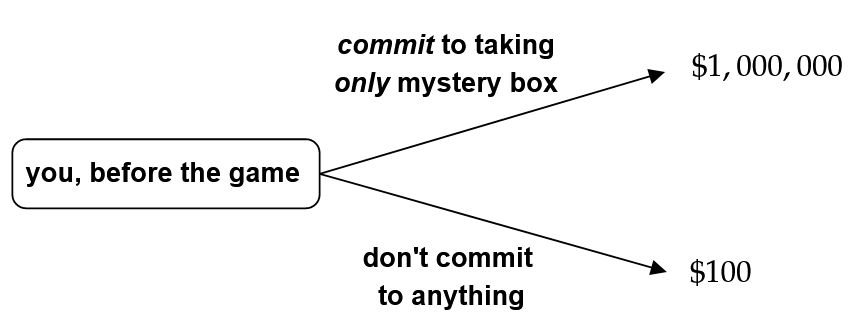
Obviously, then, if it’s before the game and you’re able to commit to being the type of person who only takes the mystery box, then you want to do so.

You would want to commit to being the type of person who – “irrationally”, quote unquote – only takes the mystery box. You would want to tie your hands, to modify your brain, to edit your DNA – to commit to being a religious one-boxer. You want to be Odysseus on his ship, tied to the mast.
 

V. It’s essential to be precise about timing

So to summarize, what’s the answer to, “Should you one-box or two-box?”?

The answer is, it depends on from which point in time you are making your decision. In the moment: you should two-box. But if you’re deciding beforehand and able to commit, you should commit to one-boxing.

How does this work out in real life? In real life, you should – right now, literally right now – commit to being the type of person who if ever placed in this situation would only take the 1-box. Impose a moral code on yourself, or something, to serve as a commitment device. So that if anyone ever comes to you with such a prediction machine, you can become a millionaire 😊.

This is of course what’s known as the problem of “time consistency”: what you want to do in the moment of choice is different from what you-five-minutes-ago would have preferred your future self to do. Another example would be that I’d prefer future-me to only eat half a cookie, but if you were to put a cookie in front of me, sorry past-me but I’m going to eat the whole thing.

Thus my claim: Newcomb merely highlights the issue of time consistency.

So why does Newcomb’s problem produce so much confusion? When describing the problem, people typically conflate and confuse the two different points in time from which the problem can be considered. In the way the problem is often described, people are – implicitly, accidentally – jumping between the two different points of view, from the two different points in time. You need to separate the two possibilities and consider them separately. I have some examples in the appendix at the bottom of this type of conflation.

Once they are cleanly separated, expected utility maximization gives the correct answer in each of the two possible – hypothetical – problems.

VI. Time consistency and macroeconomics

I say Newcomb “merely” highlights the issue of time consistency, because the idea of time consistency is both well-known and completely non-paradoxical. No new decision theories needed.

But that is not at all to say the concept is trivial! Kydland and Prescott won a Nobel Prize (in economics) for developing on the insight in a range of economic applications. In particular, they highlighted that time consistency may be an issue for central banks. I don’t want to explain in detail here the problem, but if you’re not familiar here’s one summary. What I do want to draw out is a couple of points.

Frydman, O’Driscoll, and Schotter (1982) have a fairly obscure paper that, to my (very possibly incomplete) knowledge, is the first paper arguing that Newcomb’s problem is really just a time consistency problem. It does so by pointing out that the time consistency problem facing a central bank is, literally, isomorphic to Newcomb’s problem. Broome (1989), which also is nearly uncited, summarizes Frydman-O’Driscoll-Schotter and makes the point more clearly.

Here are the two game tables for the two problems, from Broome:

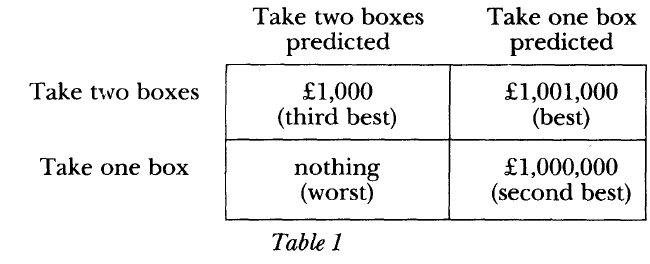
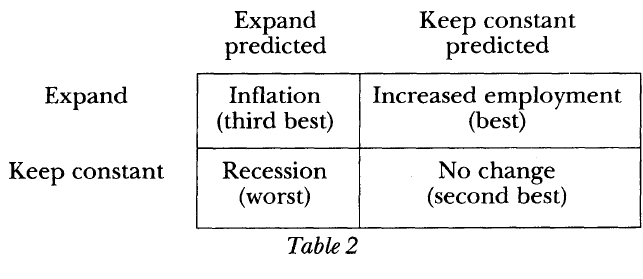
On the left, Newcomb’s problem; on the right, the Kydland-Prescott central bank problem. You can see that the rankings of the different outcomes are the exact same.

The two decision problems – the two games – are completely equivalent!

In macroeconomics we know how to state, describe, and solve this problem in formal mathematical language using the tools of standard, textbook decision theory. See Kydland and Prescott (1977) for the math if you don’t believe me! It’s just a standard optimization problem, which can be written at two possible points in time, and therefore has two possible answers.

Thus in philosophy, Newcomb’s problem can be solved the exact same way as we do it in macro, using the standard, textbook decision theory. And thus in artificial intelligence research, Newcomb’s problem can be decided by an AI in the same way that the Federal Reserve decides on monetary policy.

Philosophers want to talk about “causal decision theory” versus “evidential decision theory” versus more exotic things, and frankly I cannot figure out what those words mean in contexts I care about, or the meaning of those words when translation to economics is attempted. Why do we need to talk about counterfactual conditionals? Or perhaps equivalently: shouldn‘t we treat the predictor as an agent in the game, rather than as a state of the world to condition on?

(Eliezer Yudkowsky comments briefly on a different connection between Newcomb and monetary policy here. “Backwards causality” and “controlling the past” are just extremely common and totally normal phenomena in dynamic economics!)

(Woodford 1999 section 4 on the ‘timeless perspective’ for optimal monetary policy is another relevant macro paper here. Rather than expand on this point I’ll just say that the timeless perspective is a [very correct] argument for taking a particular perspective on optimal policy problems, in order to avoid the absurdities associated with the ‘period-0 problem’, not an alternative form of decision theory.)

VII. Steelmanning the opposing view

Some very smart people insist that Newcomb-like problems are a Big Deal. If you stuck a gun to my head and forced me to describe the most charitable interpretation of their work, here’s how I would describe that effort:

“We want to come up with a form of decision theory which is immune to time consistency problems.”

I have not seen any researchers working in this area describe their objective that way. I think it would be extremely helpful and clarifying if they described their objective that way – explicitly in terms of time consistency problems. Everyone knows what time consistency is, and using this language would make it clear to other researchers what the objective is.

I think such an objective is totally a fool’s errand. I don’t have an impossibility proof – if you have ideas, let me know – but time consistency problems are just a ubiquitous and completely, utterly normal feature in applied theory.

You can ensure an agent never faces a time consistency problem by restricting her preferences and the set of possible environments she faces. But coming up with a decision theory that guarantees she never faces time consistency problems for any preference ordering or for any environment?

It’s like asking for a decision theory that never ever results in an agent facing multiple equilibria, only a unique equilibrium. I can ensure there is a unique equilibrium by putting restrictions on the agent’s preferences and/or environment. But coming up with a decision theory that rules out multiple equilibria always and everywhere?

No, like come on, that’s just a thing that happens in the universe that we live in, you’re not going to get rid of it.

(Phrasing this directly in terms of AI safety. The goal should not be to build an AI that has a decision algorithm which never is time inconsistent, and always cooperates in the prisoners‘ dilemma, and never generates negative externalities, and always contributes in the public goods game, and et cetera. The goal should be to build up a broader economic system with a set of rules and incentives such that, in each of these situations, the socially optimal action is privately optimal – for all agents both carbon-based and silicon, not just for one particular AI agent.)

VIII. Meta comment: the importance of staying tethered to reality

For me and for Frydman-O’Driscoll-Schotter, analyzing Newcomb as a time consistency problem was possible because of our backgrounds in macroeconomics. I think there’s a meta-level lesson here on how to make progress on answering big philosophical questions.

Answering big questions is best done by staying tethered to reality: having a concrete problem to work on lets you make progress on the big picture questions. Dissolving Newcomb’s problem via analogy to macroeconomics is an example of that.

As Cameron Harwick beautifully puts it, “Big questions can only be competently approached from a specialized research program”. More on that from him here as applied to monetary economics – the field which, again, not coincidentally has been at the heart of my own research. This is also why my last post, while nominally about monetary policy, was really about ‘what is causality’ (TLDR: causality is a property of the map, not of the territory).

Scott Aaronson has made a similar point: “A crucial thing humans learned, starting around Galileo’s time, is that even if you’re interested in the biggest questions, usually the only way to make progress on them is to pick off smaller subquestions: ideally, subquestions that you can attack using math, empirical observation, or both”. He goes on to say:

For again and again, you find that the subquestions aren’t nearly as small as they originally looked! Much like with zooming in to the Mandelbrot set, each subquestion has its own twists and tendrils that could occupy you for a lifetime, and each one gives you a new perspective on the big questions. And best of all, you can actually answer a few of the subquestions, and be the first person to do so: you can permanently move the needle of human knowledge, even if only by a minuscule amount. As I once put it, progress in math and science – think of natural selection, Godel’s and Turing’s theorems, relativity and quantum mechanics – has repeatedly altered the terms of philosophical discussion, as philosophical discussion itself has rarely altered them!

Another framing for this point is on the importance of feedback loops, e.g. as discussed by Holden Karnofsky here. Without feedback loops tethering you to reality, it’s too easy to find yourself floating off into space and confused on what’s real and what’s important.

(Choosing the right strength of that tether is an art, of course. Microeconomics friends would probably tell me that monetary economics is still too detached from reality – because experiments are too difficult to run, etc. – to make progress on understanding the world!)

A somewhat narrower, but related, lesson: formal game theory is useful and in fact essential for thinking about many key ideas in philosophy, as Tyler Cowen argued in his review of Parfit’s On What Matters: “By the end of his lengthy and indeed exhausting discussions, I do not feel I am up to where game theory was in 1990”. (A recent nice example of this, among many, is Itai Sher on John Roemer“s notion of Kantian equilibrium.)

IX. Dissolving the question, dissolving confusion

Let me just restate the thesis to double down: The answer to Newcomb’s problem depends on from which point in time the question is being asked. There’s no right way to answer the question without specifying this. When the problem is properly specified, there is a time inconsistency problem: in the moment, you should two-box; but if you’re deciding beforehand and able to commit, you should commit to one-boxing.

Thanks to Ying Gao, Philipp Schoenegger, Trevor Chow, and Andrew Koh for useful discussions.

Appendix A: On “program equilibria” and “contractible contracts”

Some decision theory papers in this space (e.g. 1, 2) use the Tennenholz (2003) notion of a “program equilibrium” when discussing these types of issues. This equilibrium concept is potentially quite interesting, and I’d be interested in thinking about applications to other econ-CS domains. (See e.g. recent work on collusion in algorithmic pricing by Brown and MacKay.)

What I want to highlight is that: the definition of program equilibrium sort of smuggles in an assumption of commitment power!

The fact that your choice consists of “writing a computer program” means that after you’ve sent off your program to the interpreter, you can no longer alter your choice. Imagine instead that you could send in your program to the interpreter; your source code would be read by the other player; and then you would have the opportunity to rewrite your code. This would bring the issue of discretion vs. commitment back into the problem.

Thus the reason that program equilibria can give the “intuitive” type of result: it implicitly assumes a type of commitment power.

This very well might be the most useful equilibrium concept for understanding some situations, e.g. interaction between DAOs. But it’s clearly not the right equilibrium concept for every situation of this sort – sometimes agents don’t have commitment power.

The work of Peters and Szentes (2012) on “contractible contracts” is similar – where players can condition their actions on the contracts of other players – and they do explicitly note the role of commitment from the very first sentence of the paper.

Appendix B: Examples of conflating points in time

One example of the conflation is Nate Soares’ fantastically clear exposition here, where he writes, “You (yesterday) is the algorithm implementing you yesterday. In this simplified setting, we assume that its value determines the contents of You (today)”. This second sentence, clearly, brings in an assumption of commitment power.

Another is on this Arbital page. Are you in the moment in an ultimatum game, deciding what to do? Or are you ex ante deciding how to write the source code for your DAO, locking in the DAO’s future decisions? The discussion conflates two possible temporal perspectives.

A similar example is here from Eliezer Yudkowsky (who I keep linking to as a foil only because, and despite the fact that, he has deeply influenced me):

I keep trying to say that rationality is the winning-Way, but causal decision theorists insist that taking both boxes is what really wins, because you can’t possibly do better by leaving $1000 on the table... even though the single-boxers leave the experiment with more money.

In a static version of the game, where you’re deciding in the very moment, no! Two-boxers walk away with more money – two-boxers win more. One-boxers only win in the dynamic version of the game; or in a repeated version of the static game; or in a much more complicated version of the game taking place in reality, instead of in our separate hypothetical plane, where there’s the prospect of repeated such interactions in the future.

(My very low-confidence, underinformed read is that Scott Garrabrant’s work on ‘finite factored sets’ and ‘Cartesian frames’ gets closer to thinking about Newcomb this way, by gesturing at the role of time. But I don’t understand why the theory that he has built up is more useful for thinking about this kind of problem than is the standard theory that I describe.)

I‘m not necessarily convinced that the problem is actually well-defined, but the cloned prisoners’ dilemma also seems like a time consistency problem. Before you are cloned, you would like to commit to cooperating. After being cloned, you would like to deviate from your commitment and defect.

A final example is Parfit’s Hitchhiker, which I will only comment extremely briefly on to say: this is just obviously an issue of dynamic inconsistency. The relevant actions take place at two different points in time, and your optimal action changes over time.