I replicated this review, which you can check out in this colab notebook (I get much higher performance running it locally on my 20-core CPU).
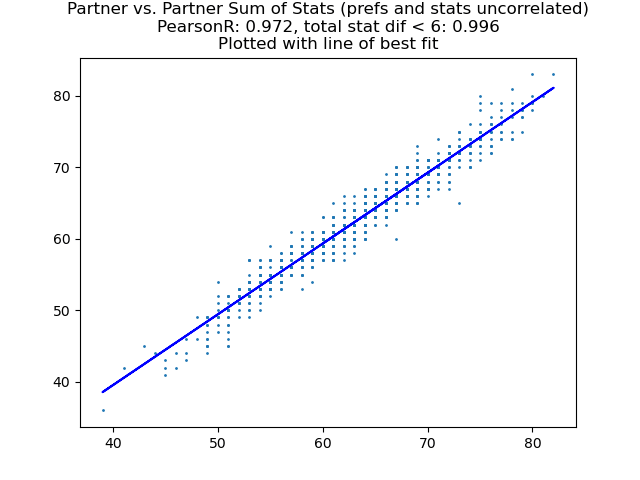
There is only one cluster of discrepancies I found between my analysis and Vaniver's: in my analysis, mating is even more assortative than in the original work:
- Pearson R of the sum of partner stats is 0.973 instead of the previous 0.857
- 99.6% of partners have an absolute sum of stats difference < 6, instead of the previous 83.3%.
- I wasn't completely sure if Vaniver's "net satisfaction" was the difference of self-satisfaction and satisfaction with partner or perhaps the log average ratio. I used the difference (since theoretically self-satisfaction could be zero, which would make the ratio undefined). Average net satisfaction was downshifted from Vaniver's result. The range I found was , while Vaniver's was .
In Vaniver's analysis, represents an adjustable correlation between a person's preferences and their own traits. Higher values of result in a higher correspondence between one's own preferences and one's own traits.
One important impact of this discrepancy is that the transition between being on average more self-satisfied than satisfied with one's partner occurs at around rather than , which intuitively makes sense to me, given the highly assortative result and the fact that the analysis directly mixture an initial set of preferences with some random data to form the final preferences as a function of .

Can we ground these results in empirical data, even though we can't observe preferences and stats with the same clarity and comprehensiveness in real-world data?
One way we can try is to consider the "self-satisfaction" metric we are producing in our simulation to be essentially the same thing as "self-esteem." There is a literature relating self-esteem to partner satisfaction in diverse cultures longitudinally over substantial periods of time. As we might expect, self-esteem, partner satisfaction, and marital satisfaction all seem to be interrelated.
- Predicting Marital Satisfaction From Self, Partner, and Couple Characteristics: Is It Me, You, or Us?
- Men and women had similar scores in personality traits of social potency, dependability, accommodation, and interpersonal relatedness.
- Broadly, self-satisfaction, partner-satisfaction, and having traits in common are all positively associated with marital satisfaction.
- Partner Appraisal and Marital Satisfaction: The Role of Self-Esteem and Depression
- "Regardless of self-esteem and depression level, and across trait categories, targets were more maritally satisfied when their partners viewed them positively and less satisfied when their partners viewed them negatively."
- The Dynamics of Self–Esteem in Partner Relationships
- "[S]elf–esteem and all three aspects of relationship quality are dynamically intertwined in such a way that both previous levels and changes in one domain predict later changes in the other domain."
- Relationships between self-esteem and marital satisfaction among women
- "Marital satisfaction was found to be positively correlated with self-esteem in both cities, so that higher self-esteem was associated with greater satisfaction."
- Development of self-esteem and relationship satisfaction in couples: Two longitudinal studies.
- "Second, initial level of self-esteem of each partner predicted the initial level of the partners’ common relationship satisfaction, and change in self-esteem of each partner predicted change in the partners’ common relationship satisfaction. Third, these effects did not differ by gender and held when controlling for participants’ age, length of relationship, health, and employment status. Fourth, self-esteem similarity among partners did not influence the development of their relationship satisfaction. The findings suggest that the development of self-esteem in both partners of a couple contributes in a meaningful way to the development of the partners’ common satisfaction with their relationship."
- A Mediation Role of Self-Esteem in the Relationship between Marital Satisfaction and Life Satisfaction in Married Individuals
- "According to the findings of the study, the mediation self-esteem between the marital satisfaction and life satisfaction was statistically significant (p<.001). The whole model was significant (F(5-288)= 36.71, p<.001) and it was observed that it explained 39% of the total variance in the life satisfaction. Self-esteem was positively associated with marital satisfaction and considered one of the most important determinants of life satisfaction."
Finally, I wonder what the value of is likely to be for participants of rationalist culture? A culture that promotes individual agency and self-improvement, that acknowledges serious challenges in our dating culture, our culture's egalitarian values, the far larger degree of control we have over ourselves than our partners, and the tendency for people to seek a self-justifying, optimistic narrative, all seem to me to point in the direction of being high. That would suggest a rationalist culture with perhaps higher levels of self-esteem than partner-esteem. Fortunately, that says nothing at all about the absolute level of self- and partner-esteem, which I hope are on average high.
I can't disagree with Vaniver's conclusion that people are "mostly being serious" when they describe their partner as their better half. But I think the results of my reanalysis and my speculation on the value of `corr` (at least in rationalist-type culture) make me think this isn't because people are accurately appraising their partner as satisfying their own preferences better than they do themselves.
I looked around a bit more on Google Scholar (to be honest, just starting with the phrase "my better half"), and found a couple studies.
- My Better Half: Strengths Endorsement and Deployment in Married Couples
- "The present study focuses on married partners’ strengths endorsement and on their opportunities to deploy their strengths in the relationship, and explores the associations between these variables and both partners’ relationship satisfaction. The results reveal significant associations of strengths endorsement and deployment with relationship satisfaction, as expected. However, unexpectedly, men’s idealization of their wives’ character strengths was negatively associated with relationship satisfaction."
- This is on a scale from 1-5 (p < .05).
Is it me or you? An actor-partner examination of the relationship between partners' character strengths and marital quality
- "[W]e examined the effects of three strengths factors (caring, self-control, and inquisitiveness) of both the individual and the partner on marital quality, evaluated by indices measuring marital satisfaction, intimacy, and burnout. Our findings revealed that the individual’s three strengths factors were related to all of his or her marital quality indices (actor effects). Moreover, women’s caring, inquisitiveness and self-control factors were associated with men’s marital quality, and men’s inquisitiveness and self-control factors were associated with women’s marital quality (partner effects)."
So idealizing your partner looks like a neutral-to-negative behavior. Inquisitiveness looks like a trait that both genders value. It strikes me that there are many things that you can do for your partner that they can't do for themselves - positive and negative. They can't praise or idealize themselves (or it won't come off the same way, anyway). They can't ask themselves "how was your day?" They can't give themselves a hug in a difficult moment, or if they do, it doesn't feel the same as when their partner does it.
No matter how effective you are at operating in the world, there are certain things that you just cannot do for yourself. In many areas of life, only your partner can. That seems like good reason to call them your better half.
Congratulations on getting married!
In the Gale-Shapley algorithm, there is an asymmetry between the two genders. One gender (typically the male) is proposing while the other is choosing. The resulting matching is the optimal stable matching for each member of the proposing gender, so I would think it makes a huge difference for your expected level of satisfaction if you belong to the proposing gender or the choosing gender.
Are your statistics about both genders or just one of them? In either case, I would love to see separate statistics for the two genders.
Thanks!
I would think it makes a huge difference for your expected level of satisfaction if you belong to the proposing gender or the choosing gender.
For the simulations I ran, it was a pretty small difference, with the proposing gender typically (but not always) having an edge. Rerunning it now (with corr=0), I get an average other-satisfaction of 23.89 for proposers and 23.77 for reviewers.
Congratulations! I enjoyed reading this, it makes me slightly more optimistic towards towards dating.
This post is very cute. I also reference it all the time to explain the 'inverse cat tax.' you You can ask my colleagues, I definitely talk about that model a bunch. So, perhaps strangely, this is my most-referenced post of 2022. 🙃
My explanation of a model tax: this forum (and the EA Forum) really like models, so to get a post to be popular, you gotta put in a model.
Great post! Intuitively, it feels like allowing for negative preferences (i.e. disliking something that other people like, like chattiness or introversion) would actually increase equitableness and maybe allow for increased other-satisfaction. (Depending on what distribution we draw people from)
Rerunning the sim with 'non-negative preferences', I get an average self-satisfaction of 21.44 and average other-satisfaction of 23.82; doing it with a random preference direction I get an average self-satisfaction of 0.53 and average other-satisfaction of 5.43 (with 95% preferring their partner). So with preferences that are less correlated between people, the matching has more ability to drive up other-satisfaction, which makes sense.
[I was expecting the average self-satisfaction to be 0, so I'm not quite sure why it's so high; maybe the randomness of the simulations is high enough that's a reasonable result? Running it some more times I get 0.28, -0.37, 0.10, -0.13, and -0.04 for self-satisfaction averages, which seems consistent with "you had an abnormally pleased group that time, but the average is 0".]
(I'm noticing I divided by net numbers by 2, which means they're "per-relationship" numbers instead of "per-person" numbers, and that was probably a mistake; oops!)

I got married today, to the particular fellow mentioned in my Turning 30 post. In a sort of 'inverse cat tax'[1] for a sappy announcement, here's a mathematical model of whether you should expect to like your partner more than yourself. I don't mean this in a moralistic way ('thou shalt love thy parents'), tho that might be another post for another time, or necessarily in a utilitarian way ("I would rather they get this ice cream than me"), but as a matter of raw respect ("I think they're a better person than I am, according to my values").
For simplicity's sake, let's consider everyone as having a 'stat' vector and a 'preferences' vector with the same dimensionality, and giving a candidate partner a 'score' based on the dot product of those two vectors. We'll assume that all of the stats are universally good (no one ever prefers an uglier partner over a prettier one, tho they might not care about physical attractiveness much). The preferences vector we'll normalize to have unit magnitude (so it's just an angle in N-dimensional space, basically, defined as a point on the positive sector of the N-spherical shell). For reasons, I'll run simulations with the stat vector as 6 dimensions with 3d6 per stat, leading to a discrete distribution a bit like a truncated normal, with no correlation between the stats.[2]
Let's start by considering the heterosexual version of the stable marriage problem, in which people partner up using the well-known Gale-Shapley algorithm, and a simulation with 1,000 each of randomly sampled men and women. Mating is highly assortative; a correlation between total stats of 85.7%, with 83.3% of people have an average total stat difference of less than 6 (the dimensionality).
The interesting result is that 91% of people like their partner at least as much as they like themselves, with an average net satisfaction of 1.24. Note that we haven't baked in any correlation between one's stats and one's preferences, and so this result is, in some sense, not very surprising. The preferences are exerting pressure on the partner (thru who you can stably match with) and not exerting pressure on the self, and so you should expect that pressure to result in higher other-satisfaction.[3]
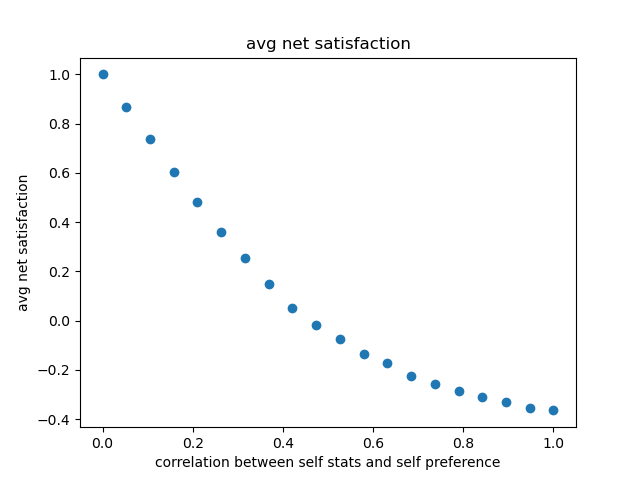
So let's add an adjustment to the preferences with a scalable parameter
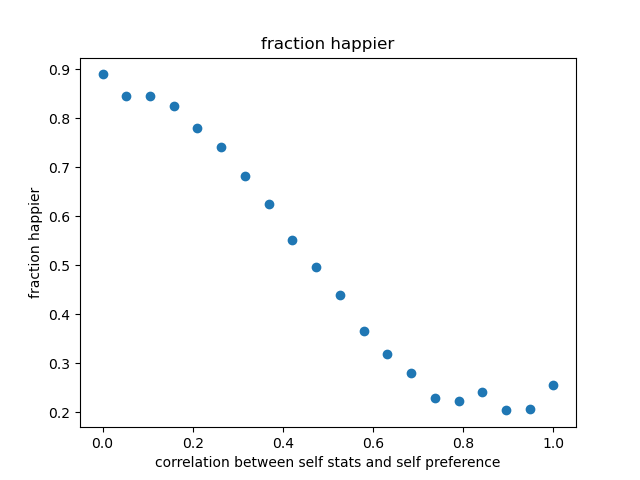
corr, so that now it's the (renormalized) sum of the stat vector (timescorr) and the previous preference vector (timesabs(1 - corr)). As we smoothly vary this from 0 to 1, the average net satisfaction decreases to -0.2 (liking themselves more than their partner) and the fraction happier decreases to 21%.While the change in net satisfaction is relatively smooth, the change in fraction happier looks much more sigmoidal, with the main drop between
corr = 0.4andcorr = 0.8. The main change here is in self-satisfaction, which increases by about 5 points while other-satisfaction increases by only about 3 points.You can also imagine situations where people specifically want their complements, rather than their mirror. Negative correlations between your stats and your preferences seem unlikely; a more appropriate model seems to be something like relationship satisfaction being a function of the minimum stat between the two partners (or the minimum plus half the maximum, or so on).
The 'marriage' situation with full bisexuality is typically called the stable roommate problem, solved with a similar algorithm. I'll leave it as an exercise for the reader how that impacts the results.[4]
Anyway, my sense is that when people talk about their 'better half', they're mostly being serious, and this is something that can easily be symmetric.
On Imgur, it's common for cat owners to end posts that collect images of use for some other reason with a picture of their cat, referred to as the 'cat tax'.
Of course in the real world, everything is correlated; not only is there g for intelligence, but GFP for personality, and wealth causes many material factors to be correlated, and so on. You could try to rationalize this by splitting out the 'natural' variables (like intelligence and wealth) into corrected variables (like intelligence and intelligence-adjusted wealth), but then it seems odd to have a uniformly random preference vector (as intelligence in the intelligence-adjusted model is more important than in the non-intelligence-adjusted model, given that some wealth-preference has now been moved over to intelligence). I currently don't expect that taking this into account will affect the analysis much (tho doing the analysis with univariate Gaussian stats leads to some odd effects with self-satisfaction, which I'm avoiding here to keep things simple).
Correlation between stats and self-satisfaction, of course, is high (0.69), because we insisted that the preferences all be positive, and so people with higher stats will like themselves more accordingly.
Naively, I would expect that everyone is more satisfied with their relationships (as they can sample from a wider pool). I think it's likely more assortative in terms of total stats, but it's a little unclear what will happen with the similarity (as
corrincreases) and what will happen to the crossover point of average net satisfaction (but I'd guess the 0 point is a bit to the right, with the 'increased satisfaction' effect swamping the 'when you try for people similar to you, you can get closer' effect).