Suppose that is a set and we have functions . Recall that for , we say that is a Pareto improvement over if for all , we have . And we say that it is a strong Pareto improvement if in addition there is some for which . We call a Pareto optimum if there is no strong Pareto improvement over it.
Theorem. Let be a set and suppose for are functions satisfying the following property: For any and any , there exists an such that for all , we have .
Then if an element of is a Pareto optimum, then there exist nonnegative constants such that the function achieves a maximum at .
Proof. Let . By hypothesis, the image is convex.
For , let the Pareto volume of be the set
This is a closed convex set. Note that is a Pareto optimum precisely when . Let's assume that this is the case; we just have to prove that maximizes for some choice of .
It suffices to find a hyperplane that contains and that supports. Then the desired function can be constructed by ensuring that is a level set.
If lies in a proper affine subspace of , let be the smallest such subspace. Let be the interior of in and let be the interior of . The case where is a point is trivial; suppose it's not, so is nonempty. By convexity, is the closure of and is the closure of .
Since is convex, is convex, and we can exhaust with a nested sequence of nonempty compact convex sets . And is convex, so we can exhaust with a nested sequence of nonempty compact convex sets . By the hyperplane separation theorem, for each , there is a hyperplane separating and . I claim that has a convergent subsequence. Indeed, each must intersect the convex hull of , and the space of hyperplanes intersecting that convex hull is compact. So has a subsequence that converges to a hyperplane .
It's easy to see that separates from for each , and so separates from . So must contain and support .
Note that the theorem does not guarantee the existence of a Pareto optimum. But if is closed and bounded, then a Pareto optimum exists.
A limitation of the theorem is that it assumes a finite list of values , not an infinite one.
Appendix to: A fungibility theorem
Suppose that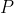 is a set and we have functions
is a set and we have functions 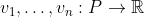 . Recall that for
. Recall that for 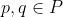 , we say that
, we say that 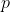 is a Pareto improvement over
is a Pareto improvement over 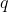 if for all
if for all 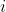 , we have
, we have  \geq v_i(q)) . And we say that it is a strong Pareto improvement if in addition there is some
. And we say that it is a strong Pareto improvement if in addition there is some 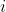 for which
for which  > v_i(q)) . We call
. We call 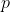 a Pareto optimum if there is no strong Pareto improvement over it.
a Pareto optimum if there is no strong Pareto improvement over it.
Theorem. Let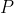 be a set and suppose
be a set and suppose 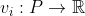 for
for 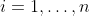 are functions satisfying the following property: For any
are functions satisfying the following property: For any 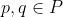 and any
and any ![\alpha \in [0, 1]](http://www.codecogs.com/png.latex?\alpha \in [0, 1]) , there exists an
, there exists an 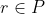 such that for all
such that for all 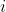 , we have
, we have  = \alpha v_i(p) + (1 - \alpha) v_i(q)) .
.
Then if an element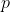 of
of 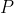 is a Pareto optimum, then there exist nonnegative constants
is a Pareto optimum, then there exist nonnegative constants 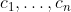 such that the function
such that the function 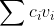 achieves a maximum at
achieves a maximum at 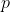 .
.
Proof. Let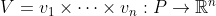 . By hypothesis, the image
. By hypothesis, the image ) is convex.
is convex.
For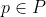 , let the Pareto volume of
, let the Pareto volume of 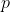 be the set
be the set
This is a closed convex set. Note that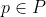 is a Pareto optimum precisely when
is a Pareto optimum precisely when  \cap V(P) = \{ V(p) \}) . Let's assume that this is the case; we just have to prove that
. Let's assume that this is the case; we just have to prove that 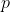 maximizes
maximizes 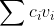 for some choice of
for some choice of 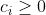 .
.
It suffices to find a hyperplane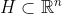 that contains
that contains ) and that supports
and that supports ) . Then the desired function
. Then the desired function 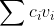 can be constructed by ensuring that
can be constructed by ensuring that 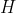 is a level set.
is a level set.
If) lies in a proper affine subspace of
lies in a proper affine subspace of 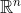 , let
, let 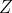 be the smallest such subspace. Let
be the smallest such subspace. Let 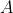 be the interior of
be the interior of ) in
in 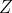 and let
and let 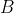 be the interior of
be the interior of ) . The case where
. The case where ) is a point is trivial; suppose it's not, so
is a point is trivial; suppose it's not, so 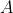 is nonempty. By convexity,
is nonempty. By convexity, ) is the closure of
is the closure of 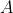 and
and ) is the closure of
is the closure of 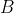 .
.
Since) is convex,
is convex, 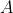 is convex, and we can exhaust
is convex, and we can exhaust 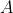 with a nested sequence of nonempty compact convex sets
with a nested sequence of nonempty compact convex sets 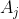 . And
. And ) is convex, so we can exhaust
is convex, so we can exhaust 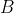 with a nested sequence of nonempty compact convex sets
with a nested sequence of nonempty compact convex sets 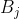 . By the hyperplane separation theorem, for each
. By the hyperplane separation theorem, for each 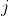 , there is a hyperplane
, there is a hyperplane 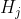 separating
separating 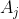 and
and 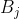 . I claim that
. I claim that 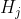 has a convergent subsequence. Indeed, each
has a convergent subsequence. Indeed, each 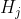 must intersect the convex hull of
must intersect the convex hull of 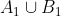 , and the space of hyperplanes intersecting that convex hull is compact. So
, and the space of hyperplanes intersecting that convex hull is compact. So 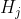 has a subsequence that converges to a hyperplane
has a subsequence that converges to a hyperplane 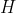 .
.
It's easy to see that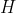 separates
separates 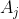 from
from 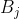 for each
for each 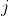 , and so
, and so 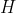 separates
separates 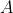 from
from 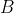 . So
. So 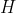 must contain
must contain ) and support
and support ) .
.
Note that the theorem does not guarantee the existence of a Pareto optimum. But if) is closed and bounded, then a Pareto optimum exists.
is closed and bounded, then a Pareto optimum exists.
A limitation of the theorem is that it assumes a finite list of values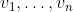 , not an infinite one.
, not an infinite one.