I think I found a clearer way to state an argument that I and a few others have been trying to make. Sorry for the repetition if you already understood! The claim is that Pareto-optimal is not equivalent to utility weighting, in the following important sense:
Consider a decision procedure as a function from a set of feasible outcomes (lotteries over world-histories) to a particular outcome. Let's say we have a decision procedure that is guaranteed to always output Pareto optimal outcomes, against some set of utility functions. Is this decision procedure necessarily equivalent to maximizing EU using a linear aggregation of those utility functions? No, because for different feasible sets, you may need different weights on the individual utility functions to reach the decisions that the original decision procedure would make, in which case we cannot specify an equivalent function using EU maximization.
(Feedback requested as to whether this made the argument clearer to anyone.)
Ah yes, this is clear to me.
Now, if we have a prior over the possible sets of lotteries you'll be presented with, then for each decision procedure and each utility function, we have the expected utility given that you follow that decision procedure. These expected utilities give us a new sense of Pareto optimality: A non-optimizing decision procedure that is Pareto-optimal in your sense will not be Pareto-optimal with respect to these expected utilities.
So, Pareto-optimal decision procedure is not equivalent to utility weighting, but Pareto-optimal (decision-procedure + prior) is equivalent to utility weighting.
The complete class theorem gives a reason for having a prior, but it assumes that you're an optimizer :)
Now, if we have a prior over the possible sets of lotteries you'll be presented with, then for each decision procedure and each utility function, we have the expected utility given that you follow that decision procedure. These expected utilities give us a new sense of Pareto optimality: A non-optimizing decision procedure that is Pareto-optimal in your sense will not be Pareto-optimal with respect to these expected utilities.
Benja answered a similar point recently in this comment, in his third paragraph which starts with "I disagree". If you apply the Pareto-optimal decision procedure to the prior instead of after updating, then it will be Pareto-optimal with respect to these expected utilities. And in general, given different priors the decision will be equivalent to maximizing different linear aggregations of individual utility functions, so you still have the same issue that the decision procedure as a function cannot be reproduced by EU maximization of a single linear aggregation.
You might ask, why does this matter if in real life we just have one prior to deal with? I guess the answer is that it's a way of making clear that a Pareto-optimal decision procedure need not be algorithmically equivalent to EU maximization, so we can't conclude that we should become EU maximizers instead of implementing some other algorithm, at least not based just on considerations of Pareto optimality.
ETA: Your response to this comment seems to indicate a misunderstanding. It's probably easier to clear up this via online chat. I sent you a PM with my contact info.
Suppose you have a prior over all possible priors, and your first action after determining your utility function is to figure out which prior you should use. Before choosing a particular prior, you can define the expected utility of policies in terms of the "expected prior" of your distribution over priors. No matter how you arrived at your utility function, you will want to remember it as a linear combination of values while updating on the prior you chose.
So if I understand you correctly, if I wanted to switch from a non-optimizing policy to an optimizing policy, I'd have to choose whether to switch to a policy that's Pareto-optimal with respect to my current beliefs, or to a policy that's Pareto-optimal with respect to old beliefs. And if we don't know which beliefs to use, we can hardly say that we "should" choose one or the other.
Is that statement close to your point of view?
No, because for different feasible sets
It's not clear to me what you mean by different feasible sets. Do you think your objection holds if you limit 'different feasible sets' to subsets of the original set that you picked the weights over?
Sorry, I'm having trouble making sense of your question, and don't know how to formulate an answer that is likely to make sense to you. Is there anyone who understands both of our perspectives, and can help bridge the gap between us? (ETA: My point is essentially the same as kilobug's. Does that version make any more sense to you? ETA2: Never mind, I guess not based on your discussions with him on other threads.)
Let's walk through a simplified example, and see if we can find the point of disagreement. The primary simplification here is that I'll assume consequentialism, where utilities are mappings from outcomes to reals and the mapping from policies (i.e. a probabilistic collection of outcomes) to reals is the probabilistically weighted sum of the outcome utilities. Even without consequentialism, this should work, but there will be many more fiddly bits.
So, let's suppose that the two of us have a joint pool of money, which we're going to spend on a lottery ticket, which could win one of three fabulous prizes (that we would then jointly own):
- A Koala (K)
- A Lemur (L)
- A Macaw (M)
- Nothing (N)
We can express the various tickets (which all cost the same, and together we can only afford one) as vectors, like a=(.1,.1,.1,.7), which has a 10% chance of delivering each animal, and a 70% chance of delivering Nothing, or b=(.2,.02,.02,.76), which has a 20% chance of delivering a Koala, 76% chance of Nothing, and 2% chance for each of the Lemur and Macaw. Suppose there are three tickets, and the third is c=(0,.3,.04,.66).
By randomly spinning a wheel to determine which ticket we want to buy, we have access to a convex combination of any of the tickets. If half the wheel points to the a ticket, and the other half points to the b ticket, our final chance of getting any of the animals will be (.15,.6,.6,.73).
Now, before we look at the tickets actually available to us, you and I eat sit down separately and imagine four 'ideal tickets'- (1,0,0,0), (0,1,0,0), (0,0,1,0), and (0,0,0,1). We can express our preferences for those as another vector: mine, V, would be, say, (3;2;1;0). (That means, for example, that I would be indifferent between a Lemur for sure and a half chance of a Koala or a Macaw, because 2=(1+3)/2.) This is a column vector, and we can multiply a*V to get .6, b*V to get .66, and c*V to get .64, which says that I would prefer the b ticket to the c ticket to the a ticket. The magnitude of V doesn't matter, just the direction, and suppose we adjust it so that the least preferred outcome is always 0. I don't know what W, your preference vector, is; it could be any four-vector with non-negative values.
Note that any real ticket can be seen as a convex combination of the ideal tickets. It's a lottery, and so they won't let us just walk up and buy a koala for the price of a ticket, but if they did that'd be my preferred outcome. Instead, I look at the real tickets for sale, right multiply them by my preference column vector, and pick one of the tickets with the highest value, which is the b ticket.
But, the pool of money is partly yours, too; you have some preference ordering W. Suppose it's (2,4,0,1), and so a*W=1.3, b*W=1.24, and c*W=1.86, meaning you prefer c to a to b.
We can think of lots of different algorithms for determining which ticket (or convex combination of tickets) we end up buying. Suppose we want it to be consistent, i.e. there's some preference vector J that describes our joint decision. Any algorithm that doesn't depend on just your and my preference scores for the ticket being considered (suppose you wanted to scratch off our least favorite options until only one is left) will run into problems (how do you scratch off the infinite variety of convex combinations, and what happened to the probabilistic encoding of preferences?), and any function that maps from (V,W) to J that isn't a linear combination of V and W with nonnegative weights on V and W will introduce new preferences that we disagree with (assuming the combination was normed, or you have an affine combination of V and W). Suppose we pick some v and w, such that J=vV+wW; if we pick v=1 and w=1 then J=(5,6,1,1)->(4,5,0,0), a and b have the same score, and c is the clear winner. Note that, regardless of v and w, c will always be preferred to a, and the primary question is whether c or b is preferred, and that a wide range of v and w would lead to c being picked.
So far, we should be in agreement, since we haven't gotten to the issue that I think you're discussing, which sounds like: this is all fine and dandy for a, b, and c, but:
- What if we had some new set of tickets, d, e, and f? There's no guarantee that we would still agree on the same v and w.
- What if we had some new set of animals, Hippo, Ibis, and Jackal? There's no guarantee that we would still agree on the same v and w.
I think that the ideal tickets suggest that 1 isn't a serious concern. We may not have measured v and w very carefully with the tickets we had before, since even a rough estimate is sufficient to pin down our ticket choice (unless we were close to the edge), and we might be near the edge now, but supposing that we measured v and w exactly, we should be able to apply J as before.
I think that 2 is a slightly more serious concern, but I think it can be addressed.
First, we could have some constructive method of picking the weights. You and I, when deciding to pool our money to buy a lottery ticket, might have decided to normalize our preference functions some way and then combine them with weights relative to our financial contribution, or we might decide that your taste in animals is totally better than mine, and so v would be 0 and w 1, or we might decide that I'm better at arm wrestling, and V/w should be 5 after normalization. The outcomes don't play in to the weighting, and so we can be confident in the weights.
Second, we could find the weights with both lotteries in mind. The first lottery will give us an acceptable range for v/w, the second lottery will give us an acceptable range for v/w, and the two should overlap, and so we can pick one from the smaller range that satisfies both. (Is the issue that you're not sure they will overlap?)
Ok, I think what's going on is that we have different ideas in mind about how two people make joint decisions. What I have in mind is something like Nash Bargaining solution or Kalai-Smorodinsky Bargaining Solution (both described in this post), for which the the VNM-equivalent weights do change depending on the set of feasible outcomes. I have to read your comment more carefully and think over your suggestions, but I'm going to guess that there are situations where they do not work or do not make sense, otherwise the NBS and KSBS would not be "the two most popular ways of doing this".
Ah, I think I see where you're coming from now.
Note that, as expected, in all cases we only consider options on the Pareto frontier, and those bargaining solutions could be expressed as the choice made by a single agent with a normal utility function. You're right that the weights which identify the chosen solution will vary based on the options used and bargaining power of the individuals, and it's worth reiterating that this theorem does not give you any guidance on how to pick the weights (besides saying they should be nonnegative). Think of it more as the argument that "If we needed to build an agent to select our joint choice for us and we can articulate our desires and settle on a mutually agreeable solution, then we can find weights for our utility functions such that the agent only needs to know a weighted sum of utility functions," not the argument "If we needed to choose jointly and we can articulate our desires, then we can settle on a mutually agreeable solution."
The NBS and KSBS are able to give some guidance on how to find a mutually agreeable solution because they have a disagreement point that they can use to get rid of the translational freedom, and thus they can get a theoretically neat result that does not depend on the relative scaling of the utility functions. Without that disagreement point (or something similar), there isn't a theoretically neat way to do it.
In the example above, we could figure out each of our utilities for not paying our part for the ticket (and thus getting no chance to win), and decide what weights to put on based on that. But as the Pareto frontier shifts- as more tickets or more animals become available- our bargaining positions could easily shift. Suppose my utility for not buying in is .635, and your utility for not buying in is 1; I gain barely anything by buying a ticket (b is .025, c is .005), and you gain a lot (b is .24, and c is .86), and so I can use my indifference to making a deal to get my way (.025*.24>.005*.86).
But then the Ibis becomes available, as well as a ticket that offers a decent chance to get it, and I desperately want to get an Ibis. My indifference evaporates, and with it my strong bargaining position.
In situations where social utility will be aggregated, one way or another, then we don't really have a d to get rid of our translational freedom. In cases where the disagreement point is something like "everybody dies" it's not clear we want our metaethics (i.e. how we choose the weights) to be dependent on how willing someone is to let everybody die to not get their way (the old utility monster complaint).
Think of it more as the argument that "If we needed to build an agent to select our joint choice for us and we can articulate our desires and settle on a mutually agreeable solution, then we can find weights for our utility functions such that the agent only needs to know a weighted sum of utility functions,"
I still disagree with this. I'll restate/expand the argument that I made at the top of the previous thread. Suppose we want to use NBS or KSBS to make the joint choice. We could:
- Compute the Pareto frontier, apply NBS/KSBS to find the mutually agreeable solution, use the slope of the tangent at that point to derive a set of weights, use those weights to form a linear aggregation of our utility functions, program the linear aggregation into a VNM AI, have the VNM AI recompute that solution we already found and apply it, or
- Input our utility functions into an AI separately, program it to compute the Pareto frontier and apply NBS/KSBS to find the mutually agreeable solution and directly apply that solution.
It seems to me that in 1 you're manually doing all of the work to make the actual decision outside of the VNM framework, and then tacking on a VNM AI at the end to do more redundant work. Why would you do that instead of 2?
I still disagree with this.
You disagree with the statement that we can, or you disagree with the implication that we should?
Why would you do that instead of 2?
In practice, I don't think you would need to. The point of the theorem is that you always can if you want to, and I'm not sure why this result is interesting to Nisan.
(Note also that this approach works for other metaethical approaches besides NBS/KSBS, and that you don't always have access to NBS/KSBS.)
Yeah, I thought you meant to imply "should". If we're just talking about "can", then I agree (with some caveats that aren't very important at this point).
I think Vaniver might have thought, given the parenthetical about world-histories, that the original set was meant to include all possible world-histories from a given starting point.
To be sure I understand:
For any given pareto-optimal solution, there is an equivalent utility-weighing that would give the same result. However, the weights will be different for each solution. (i.e. for any given X+Y = Z, I can say that X = Z-Y, but there are infinite possible combinations of values that match this pattern.)
Therefor, "find the correct pareto-optimal solution" is more efficient, since it always results in a solvable equation, whereas "find the correct utility weights" is under-specified since it doesn't tell you HOW to determine that?
Suppose further that you can quantify each item on that list with a function from world-histories to real numbers, and you want to optimize for each function, all other things being equal.
If fairness is one of my values, it can't necessary be represented by such a function. (I.e., it may need to be a function from lotteries over world-histories to real numbers.)
What the theorem says is that if you really care about the values on that list, then there are linear aggregations that you should start optimizing for.
I think before you make this conclusion, you have to say something about how one is supposed to pick the weights. The theorem itself seems to suggest that I can pick the weights by choosing a Pareto-optimal policy/outcome that's mutually acceptable to all of my values, and then work backwards to a set of weights that would generate a utility function (or more generally, a way to pick such weights based on a coin-flip) that would then end up optimizing for the same outcome. But in this case, it seems to me that all of the real "optimizing" was already done prior to the time you form the linear aggregation.
(ETA: I guess the key question here is whether the weights ought to logically depend on the actual shape of the Pareto frontier. If yes, then you have to compute the Pareto frontier before you choose the weights, in which case you've already "optimized" prior to choosing the weights, since computing the Pareto frontier involves optimizing against the individual values as separate utility functions.)
Also, even if my values can theoretically be represented by functions from world-histories to real numbers, I can't obtain encodings of such functions since I don't have introspective access to my values, and therefore I can't compute linear aggregations of them. So I don't know how I can start optimizing for a linear aggregation of my values, even if I did have a reasonable way to derive the weights.
If you're capable of making precommitments and we don't worry about computational difficulties [...]
I'm glad you made these assumptions explicit, but shouldn't there be a similar caveat when you make the final conclusions? The way I see it, I have a choice between (A) a solution known to be optimal along some dimensions not including considerations of logical uncertainty and dynamical consistency, or (B) a very imperfectly optimized solution that nevertheless probably does take them into account to some degree (i.e., the native decision making machinery that evolution gave me). Sticking with B for now doesn't seem unreasonable to me (especially given the other difficulties I mentioned with trying to implement A).
(I've skipped some of the supporting arguments in this comment since I already wrote about them under the recent Harsanyi post. Let me know if you want me clarify anything.)
I think before you make this conclusion, you have to say something about how one is supposed to pick the weights.
I agree with this concern. The theorem is basically saying that, given any sensible aggregation rule, there is a linear aggregation rule that produces the same decisions. However, it assumes that we already have a prior; the linear coefficients are allowed to depend on what we think the world actually looks like, rather than being a pure representation of values. I think people, especially those who don't understand the proof of this theorem, are likely to misinterpret it.
I guess the key question here is whether the weights ought to logically depend on the actual shape of the Pareto frontier.
Yes, whether a set of weights leads to Pareto-dominance depends logically on the shape of the Pareto frontier. So the theorem does not help with the computational part of figuring out what one's values are.
I have a choice between (A) a solution known to be optimal along some dimensions not including considerations of logical uncertainty and dynamical consistency, or (B) a very imperfectly optimized solution that nevertheless probably does take them into account to some degree (i.e., the native decision making machinery that evolution gave me). Sticking with B for now doesn't seem unreasonable to me
Sticking with B by default sounds reasonable except when we know something about the ways in which B falls short of optimality and the ways in which B takes dynamical consistency issues into account. E.g., I can pretty confidently recommend that minor philanthropists donate all their charity to the single best cause, modulo a number of important caveats and exceptions. It's natural to feel that one should diversify their (altruistic, outcome-oriented) giving; but once one sees the theoretical justification for single-cause giving under ideal conditions and one explains away their intuitions with motives they don't endorse and heuristics that work okay in the EAA but not on this particular problem, I think they have a good reason to go with choice A.
Even then, the philanthropist still has to decide which cause to donate to. It's possible that once they believe they should construct a utility function for a particular domain, they'll be able to use other tools to come up with a utility function they're happy with. But this theorem doesn't guarantee that.
I tried not to claim too much in the OP. I hope no one reads this post and makes a really bad decision because of an overly-naive expected-utility calculation.
Yes, whether a set of weights leads to Pareto-dominance depends logically on the shape of the Pareto frontier. So the theorem does not help with the computational part of figuring out what one's values are.
Do you mean "figuring out what one's weights are"? Assuming yes, I think my point was a bit stronger than that, namely there's not necessarily a reason to figure out the weights at all, if in order to figure out the weights, you actually have to first come to a decision using some other procedure.
Sticking with B by default sounds reasonable except when we know something about the ways in which B falls short of optimality and the ways in which B takes dynamical consistency issues into account.
I think there's probably local Pareto improvements that we can make to B, but that's very different from switching to A (which is what your OP was arguing for).
E.g., I can pretty confidently recommend that minor philanthropists donate all their charity to the single best cause, modulo a number of important caveats and exceptions. It's natural to feel that one should diversify their (altruistic, outcome-oriented) giving;
I agree this seems like a reasonable improvement to B, but I'm not sure what relevance your theorem has for it. You may have to write that post you mentioned in the OP to explain.
I tried not to claim too much in the OP. I hope no one reads this post and makes a really bad decision because of an overly-naive expected-utility calculation.
Besides that, I'm concerned about many people seemingly convinced that VNM is rationality and working hard to try to justify it, instead of working on a bunch of open problems that seem very important and interesting to me, one of which is what rationality actually is.
Yes, whether a set of weights leads to Pareto-dominance depends logically on the shape of the Pareto frontier. So the theorem does not help with the computational part of figuring out what one's values are.
Do you mean "figuring out what one's weights are"?
Yes
Assuming yes, I think my point was a bit stronger than that, namely there's not necessarily a reason to figure out the weights at all, if in order to figure out the weights, you actually have to first come to a decision using some other procedure.
I think any disagreement we have here is subsumed by our discussion elsewhere in this thread.
I think there's probably local Pareto improvements that we can make to B, but that's very different from switching to A (which is what your OP was arguing for).
Perhaps I will write that philanthropy post, and then we will have a concrete example to discuss.
Besides that, I'm concerned about many people seemingly convinced that VNM is rationality and working hard to try to justify it, instead of working on a bunch of open problems that seem very important and interesting to me, one of which is what rationality actually is.
I appreciate your point.
ETA: Wei_Dai and I determined that part of our apparent disagreement came from the fact that an agent with a policy that happens to optimize a function does not need to use a decision algorithm that computes expected values.
If fairness is one of my values, it can't necessary be represented by such a function. (I.e., it may need to be a function from lotteries over world-histories to real numbers.)
You refer to cases such as A = “I give the last candy to Alice”, B = “I give the last candy to Bob” and you strictly prefer the lottery {50% A, 50% B} to {100% A} or {100% B}?
But remember that we're talking about entire world histories, not just world states -- If you take A0 = “I arbitrarily give the last candy to Alice”, A1 = “I flip a coin to decide whom to give the last candy to, and Alice wins”, etc., you can easily have A1 = B1 > A0 = B0, since A1 and A0 are different (one includes you flipping a coin, the other doesn't). So a function from world histories would suffice, after all.
I'm pretty sure Nisan meant to define "world-histories" in a way to exclude utility functions like that, otherwise it's hard to make sense of the convexity property that he assumes in his theorem. (Hopefully he will jump in and confirm or deny this.)
Yes, we should assume the agent has access to a source of uncertainty with respect to which the functions v_i are invariant.
In fact, let's assume a kind of Cartesian dualism, so that the agent (and a single fair coin) are not part of the world. That way the agent can't have preferences over its own decision procedure.
I think before you make this conclusion, you have to say something about how one is supposed to pick the weights.
I think these weights are descriptive, not prescriptive. Eliciting values is very important- and there's some work in the decision analysis literature on that- but there isn't much to be done theoretically, since most of the work is "how do we work around the limitations of human psychology?" rather than "how do we get the math right?".
I think these weights are descriptive, not prescriptive.
What do you mean by that? Are you saying humans already maximize expected utility using some linear aggregation of individual values, so these weights already exist? But the whole point of the OP is to convince people who are not already EU maximizers to become EU maximizers.
Are you saying humans already maximize expected utility using some linear aggregation of individual values, so these weights already exist?
I think my answer would be along the lines of "humans have preferences that could be consistently aggregated but they are bad at consistently aggregating them due to the computational difficulties involved." For example, much of the early statistical prediction rule work fit a linear regression to a particular expert's output on training cases, and found that the regression of that expert beat the expert on new cases- that is, it captured enough of their expertise but did not capture as much of their mistakes, fatigue, and off days. If you're willing to buy that a simple algorithm based on a doctor can diagnose a disease better than that doctor, then it doesn't seem like a big stretch to claim that a simple algorithm based on a person can satisfy that person's values better than that person's decisions made in real-time. (In order to move from 'diagnose this one disease' to 'make choices that impact my life trajectory' you need much, much more data, and probably more sophisticated aggregation tools than linear regression, but the basic intuition should hold.)
And so I think the methodology is (sort of) prescriptive: whatever you do, if it isn't equivalent to a linear combination of your subvalues, then your aggregation procedure is introducing new subvalues, which is probably a bug.* (The 'equivalent to' is what makes it only 'sort of' prescriptive.) If the weights aren't all positive, that's probably also a bug (since that means one of your subvalues has no impact on your preferences, and thus it's not actually a subvalue). But what should the relative weights for and
be? Well, that depends on the tradeoffs that the person is willing to make; it's not something we can pin down theoretically.
*Or you erroneously identified two subvalues as distinct, when they are related and should be mapped jointly.
And so I think the methodology is (sort of) prescriptive: whatever you do, if it isn't equivalent to a linear combination of your subvalues, then your aggregation procedure is introducing new subvalues, which is probably a bug.
I tried to argue against this in the top level comment of this thread, but may not have been very clear. I just came up with a new argument, and would be interested to know whether it makes more sense to you.
Neat, but this looks equivalent to Harsanyi to me. It seems to me like you make the same assumption that VNM holds for the subvalues; your are the equivalent of the agents being aggregated in Harsanyi's society. If you're inconsistent about "your welfare," then you can't aggregate that and your other subvalues into a consistent function.
Now, if someone makes that objection- "but I can't compress my welfare down to a mapping onto the reals!"- you can repeat this argument to them. Well, can you compress subsets of your welfare down to a mapping onto the reals? And if you can do that for all of the subsets, then we have a set of mappings onto the reals, which we can aggregate into a single mapping, and you were mistaken about your preference inconsistency. (Now, they might be unsure about the weights for those mappings, and there's no guarantee that you can help them pick the correct ones, but that's a measurement problem.)
I suspect this may be a more convincing argument that people should be optimizers: if the feeling of cyclical preferences is the result of uncertainty, then that uncertainty might be resolvable, whereas Dutch book arguments just argue that their preferences are a bad idea, which humans often find unconvincing. Indeed, whenever I've seen someone defend cyclical preferences, it's by altering the saliency of various variables for the various comparisons, and it seems easy to point out to them that they're not making a nuanced decision, but just making the decision based on the most salient factor, and that if they carefully measured their preferences along all relevant axes, they would know which option was the best, all things considered.
Neat, but this looks equivalent to Harsanyi to me.
Harsanyi's theorem concerns a "social welfare function" that society is supposed to maximize. The present theorem makes no such assumption.
Well, instead it concerns an "individual welfare function" that an individual is supposed to maximize, and the individual is assumed to be composed of VNM-rational subindividuals. Sure, it's a different flavor, but is there anything else different?
It only assumes the VNM-rational subindividuals, and derives the existence of the overall welfare function.
I didn't notice until reading your comment that your theorem gives an answer to the question of why the aggregation should be VNM-rational.
On the purely mathematical side, I've an issue with the theorem as stated : it says :
then if P is pareto optimal,
such as P is a maximum of
.
Which is widely different from :
such as
then if P is pareto optimal, then P is a maximum of
.
In the way the theorem is stated, you don't have a utility function with fixed coefficients you can use for every situation, but for every situation, you can find a set of coefficient that will work, which is not what being an optimizer is.
See my reply to Wei Dai's comment. If you have a prior over which situations you will face, and if you're able to make precommitments and we ignore computational difficulties, then there is only one situation. If you could decide now which decision rule you'll use in the future, then in a sense that would be the last decision you ever make. And a decision rule that's optimal with respect to a particular utility function is one that makes every subsequent decision using that same utility function.
From the vantage point of an agent with a prior today, the best thing it can do is adopt a utility function and precommit to maximizing it from now on no matter what. I hope that's more clear.
The and
are not unique. If
, then I expect
.
In the way the theorem is stated, you don't have a utility function with fixed coefficients you can use for every situation, but for every situation, you can find a set of coefficient that will work, which is not what being an optimizer is.
P is the space of situations*, and is the space of individual preferences over situations.
The actual theorem says that, for any particular situation and any particular individual, you can find a personal weighting that aggregates their preferences over that situation, and this method is guaranteed to return Pareto optimal solutions. (Choosing between Pareto optimal solutions is up to you, and is done by your choice of weightings.)
Your second version says for any particular situation, there exists a magic weighting which will aggregates the preferences of any possible individual in a way that returns solutions which are simultaneously maximized by all Pareto optimal solutions any agent produces.
Of course, there is such a magic weighting. It is the vector of all zeros, because every point in P maximizes that function, and so the Pareto optimal points will as well.
* Well, strictly, it's the space of "policies," which is a combination of what will happen to the agent and how they will respond to it, which we're describing elsewhere as a "world history."
Hum, yes, indeed I got the P and V_i backwards, sorry.
The argument still holds, but with the other inversion between the \forall and the \exists :
such as
then if P is pareto optimal, then P is a maximum of
.
Having an utility function means the weighting (the c_i) can vary between each individuals, but not between situations. If for each situation ("world history" more exactly) you chose a different set of coefficients, it's no longer an utility function - and you can make about anything with that, just choosing the coefficients you want.
That doesn't work, because is defined as a mapping from
to the reals; if you change
, then you also change
, and so you can't define them out of order.
I suspect you're confusing , the individual policies that an agent could adopt, and
, the complete collection of policies that the agent could adopt.
Another way to express the theorem is that there is a many-to-one mapping from choices of to Pareto optimal policies that maximize that choice of
.
[Edit] It's not strictly many-to-one, since you can choose s that make you indifferent between multiple Pareto optimal basic policies, but you recapture the many-to-one behavior if you massage your definition of "policy," and it's many-to-one for most choices of
.
It's likely that someone has previously used the hyperplane separation theorem to justify being an optimizer, but I don't know of any source that does that.
Will_Sawin said:
I think the fact that Pareto is equivalent to utility-weighting is well-known in economics. It's one of the consequences of the separating hyperplane theorem.
ETA: Maybe he was referring to second fundamental theorem of welfare economics?
But you are a human and you don't obey the axioms ... Suppose further that you can quantify each item on that list
Thanks for the interesting read. FWIW, this human isn't convinced that becoming a human approximation to an optimizer is worthwhile. What happens if, as is more realistic, I can't quantify any item on my list? (Or perhaps I can, but with three large error terms for environmental noise in the signal, temporal drift of the signal, and systemic errors in converting different classes of value to a common unit.)
I think that, depending on what the v's are, choosing a Pareto optimum is actually quite undesirable.
For example, let v1 be min(1000, how much food you have), and let v2 be min(1000, how much water you have). Suppose you can survive for days equal to a soft minimum of v1 and v2 (for example, 0.001 v1 + 0.001 v2 + min(v1, v2)). All else being equal, more v1 is good and more v2 is good. But maximizing a convex combination of v1 and v2 can lead to avoidable dehydration or starvation. Suppose you assign weights to v1 and v2, and are offered either 1000 of the more valued resource, or 100 of each. Then you will pick the 1000 of the one resource, causing starvation or dehydration after 1 day when you could have lasted over 100. If which resource is chosen is selected randomly, then any convex optimizer will die early at least half the time.
A non-convex aggregate utility function, for example the number of days survived (0.001 v1 + 0.001 v2 + min(v1, v2)), is much more sensible. However, it will not select Pareto optima. It will always select the 100 of each option; always selecting 1000 of one leads to greater expected v1 and expected v2 (500 for each).
Wha...?
I believe your Game is badly-formed. This doesn't sound at all like how Games should be modeled. Here, you don't have two agents each trying to maximize something that they value of their own, so you can't use those tricks.
As a result, apparently you're not properly representing utility in this model. You're implicitly assuming the thing to be maximized is health and life duration, without modeling it at all. With the model you make, there are only two values, food and water. The agent does not care about survival with only those two Vs. So for this agent, yes, picking one of the "1000" options really truly spectacularly trivially is better. The agent just doesn't represent your own preferences properly, that's all.
If your agent cares at all about survival, there should be a value for survival in there too, probably conditionally dependent on how much water and food is obtained. Better yet, you seem to be implying that the amount of food and water obtained isn't really important, only surviving longer is - strike out the food and water values, only keep a "days survived" value dependent upon food and water obtained, and then form the Game properly.
I think we agree. I am just pointing out that Pareto optimality is undesirable for some selections of "values". For example, you might want you and everyone else to both be happy, and happiness of one without the other would be much less valuable.
I'm not sure how you would go about deciding if Pareto optimality is desirable, now that the theorem proves that it is desirable iff you maximize some convex combination of the values.
Given some value v1 that you are risk averse with respect to, you can find some value v1' that your utility is linear with. For example, if with other values fixed, utility = log(v1), then v1':=log(v1). Then just use v1' in place of v1 in your optimization. You are right that it doesn't make sense to maximize the expected value of a function that you don't care about the expected value of, but if you are VNM-rational, then given an ordinal utility function (for which the expected value is meaningless), you can find a cardinal utility function (which you do want to maximize the expected value of) with the same relative preference ordering.
I didn't say anything about risk aversion. This is about utility functions that depend on multiple different "values" in some non-convex way. You can observe that, in my original example, if you have no water, then utility (days survived) is linear with respect to food.
Oh, I see. The problem is that if the importance of a value changes depending on how well you achieve a different value, a Pareto improvement in the expected value of each value function is not necessarily an improvement overall, even if your utility with respect to each value function is linear given any fixed values for the other value functions (e.g. U = v1*v2). That's a good point, and I now agree; Pareto optimality with respect to the expected value of each value function is not an obviously desirable criterion. (apologies for the possibly confusing use of "value" to mean two different things)
Edit: I'm going to backtrack on that somewhat. I think it makes sense if the values are independent of one another (not the case for food and water, which are both subgoals of survival). The assumption needed for the theorem is that for all i, the utility function is linear with respect to v_i given fixed expected values of the other value functions, and does not depend on the distribution of possible values of the other value functions.
For example, you might want you and everyone else to both be happy, and happiness of one without the other would be much less valuable.
Now you've got me curious. I don't see what selections of values representative of the agent they're trying to model could possibly desire non-Pareto-optimal scenarios. The given example (quoted), for one, is something I'd represent like this:
Let x = my happiness, y = happiness of everyone else
To model the fact that each is worthless without the other, let:
v1 = min(x, 10y)
v2 = min(y, 10x)
Choice A: Gain 10 x, 0 y
Choice B: Gain 0 x, 10 y
Choice C: Gain 2 x, 2 y
It seems very obvious that the sole Pareto-optimal choice is the only desirable policy. Utility is four for choice C, and zero for A and B.
This may reduce to exactly what AlexMennen said, too, I guess. I have never encountered any intuition or decision problem that couldn't at-least-in-principle resolve to a utility function with perfect modeling accuracy given enough time and computational resources.
I do think that everything should reduce to a single utility function. That said, this utility function is not necessarily a convex combination of separate values, such as "my happiness", "everyone else's happiness", etc. It could contain more complex values such as your v1 and v2, which depend on both x and y.
In your example, let's add a choice D: 50% of the time it's A, 50% of the time it's B. In terms of individual happiness, this is Pareto superior to C. It is Pareto inferior for v1 and v2, though.
EDIT: For an example of what I'm criticizing: Nisan claims that this theorem presents a difficulty for avoiding the repugnant conclusion if your desiderata are total and average happiness. If v1 = total happiness and v2 = average happiness, and Pareto optimality is desirable, then it follows that utility is a*v1 + b*v2. From this utility function, some degenerate behavior (blissful solipsist or repugnant conclusion) follows. However, there is nothing that says that Pareto optimality in v1 and v2 is desirable. You might pick a non-linear utility function of total and average happiness, for example atan(average happiness) + atan(total happiness). Such a utility function will sometimes pick policies that are Pareto inferior with respect to v1 and v2.
This example doesn't satisfy the hypotheses of the theorem because you wouldn't want to optimize for v1 if your water was held fixed. Presumably, if you have 3 units of water and no food, you'd prefer 3 units of food to a 50% chance of 7 units of food, even though the latter leads to a higher expectation of v1.
Ah, okay. In that case, if you're faced with a number of choices that offer varying expectations of v1 but all offer a certainty of say 3 units of water, then you'll want to optimize for v1. But if the choices only have the same expectation of v2, then you won't be optimizing for v1. So the theorem doesn't apply because the agent doesn't optimize for each value ceteris paribus in the strong sense described in this footnote.
But if the choices only have the same expectation of v2, then you won't be optimizing for v1.
Ok, this correct. I hadn't understood the preconditions well enough. It seems that now the important question is whether things people intuitively think of as different values (my happiness, total happiness, average happiness) satisfy this condition.
if you really care about the values on that list, then there are linear aggregations
Of course existence doesn't mean that we can actually find these coefficients. Even if you have only 2 well-defined value functions, finding an optimal tradeoff between them is generally computationally hard.
Additional to the purely mathematical problem stated above (but I preferred to make two different comments since they are on a totally different basis), I've a few problems with using such kind of reasoning for real life issues :
A Pareto optimal is a very weak condition. If you've a set of 10 values, and you've three possible outcomes : Outcome A is 100 for value 1, and 0 for all others. Outcome B is 99.99 for value 1, and 50 for all others. Outcome C is 99.98 for value 1, and 45 for all others. Outcome A and B are both equally Pareto optimal. But unless one value really trumps all the others, we would still prefer outcome C than outcome A, even if C isn't a Pareto optimal. But having a decision algorithm that is guaranteed to chose a Pareto optimal doesn't say if it'll take A or B. And I prefer a decision algorithm that will select the non-Pareto-optimal C than one which will select the Pareto-optimal A, in the absence of one which is guaranteed to take B (which being Pareto-optimal doesn't). (That's also an issue I've with classical economics, btw.)
Since we don't know all our values, nor how to precisely measure them (how do you evaluate the "welfare of mammals" ?), nor does the theorem give any method for selecting the coefficients, it is not very useful to take decisions on your daily life to know that such an utility function can exist. It is important when working on FAI, definitely. It may have some importance in reasoning about meta-ethics or policy making. But it's very had to apply to real life decisions.
Insisting on Pareto optimality with respect to your values does not rule out all unreasonable policies, but it does rule out a large class of unreasonable policies, without ruling out any reasonable policies. It is true that the theorem doesn't tell you what your coefficients should be, but figuring out that you need to have coefficients is a worthwhile step on its own.
Outcome A and B are both equally Pareto optimal. But unless one value really trumps all the others, we would still prefer outcome C than outcome A, even if C isn't a Pareto optimal.
This fits fine within the framework. Suppose that value 1 truly is superior to value 2 (dropping the other 8): our aggregation is f1=x1. Then, outcome A, which is a pareto optimum, also maximizes f1, with a score of 100. Suppose that all values are equal: then our aggregation is f1=x1+x2. Then, outcome B, which has d2=149.99, is superior to C at 144.98, which is superior to A at 100.
What Pareto optimality means is that you cannot find an objective function with nonnegative weights such that outcome C is the best outcome. This is a feature; any method of choosing options which doesn't choose a Pareto optimal point can be easily replaced by a method which does choose a Pareto optimal point, and so it's a good thing that our linear combination cannot fail us that way.
And I prefer a decision algorithm that will select the non-Pareto-optimal C than one which will select the Pareto-optimal A, in the absence of one which is guaranteed to take B
Pareto optimality is defined in the presence of options that could be taken. If outcome B is off the table, then outcome C becomes Pareto optimal. If you prefer a system which prefers C to A, that's a preference over the weights on the aggregating function which is easy to incorporate.
But it's very had to apply to real life decisions.
Agreed. I don't expect we'll ever get perfect measurement of values (we don't have perfect measurement of anything else), but a mediocre solution is still an improvement over a bad solution.
My point was that being Pareto-optimal is such a weak constraint that it doesn't really mater, in real life, when choosing a decision algorithm. The best possible algorithm will be Pareto-optimal, sure. But that perfect algorithm is usually not an option - we don't have infinite computing power, we don't have perfect knowledge, we don't have infinite time for the convergence towards the optimal to happen.
So when choosing between imperfect algorithms, one that is guaranteed to bring Pareto-optimal may not necessarily be better than one which doesn't. An algorithm that is guaranteed to always select answer A or B, but that will tend to select answer A, may not be as good as an algorithm with will select answer C most of the time. For example, look how so many versions of utilitarianism will collapse with utility monsters. That's a typical flaw of focusing on Pareto-optimal algorithm. More naïve ethical frameworks may not be Pareto-optimal, but they'll not consider giving everything to the utility monster to be a sane output.
Pareto-optimality is not totally useless - it's a good quality to have. But I think that we (especially economists) tend to give it much more value that it really has, it's a very weak constraints, and a very weak indicator of the soundness of an ethical framework/policy making mechanism/algorithm.
My point was that being Pareto-optimal is such a weak constraint that it doesn't really mater, in real life, when choosing a decision algorithm.
This does not agree with my professional experience; many real decisions are Pareto suboptimal with respect to terminal values.
But that perfect algorithm is usually not an option - we don't have infinite computing power, we don't have perfect knowledge, we don't have infinite time for the convergence towards the optimal to happen.
What? This is the opposite of what you just said; this is "Pareto optimality is too strong a constraint for us to be able to find feasible solutions in practical time."
I agree with you that Pareto optimality is insufficient, and also that Pareto optimality with respect to terminal values is not necessary. Note that choosing to end your maximization algorithm early, because you have an answer that's "good enough," is a Pareto optimal policy with respect to instrumental values!
I think that we understand VNM calculations well enough that most modern improvements in decision-making will come from superior methods of eliciting weights and utility functions. That said, VNM calculations are correct, should be implemented, and resistance to them is misguided. Treat measurement problems as measurement problems, not theoretical problems!
That's easy: If p and q are two policies and alpha in [0,1], the mixed policy where today you randomly choose policy p with probability alpha and policy q with probability 1-alpha, is also a policy.
But what if the value an agent assigns to life events depends on the probabilities as well as the final results? Wei Dai gave one example, a concern for fairness, that can make this true, but simple risk aversion or thrill seeking would also suffice. Then it seems to me that the interpretation of the "linear aggregation function" becomes problematic.
simple risk aversion or thrill seeking would also suffice.
Simple risk aversion can be captured in the mapping of results to reals. Prospect-theory style risk aversion, whereby small probabilities are inflated, can't be, but that's a feature, not a bug.
Thrill seeking- in the sense of deriving value from results being determined by randomness- does not seem like it can be fit into a VNM framework. That's a failing descriptively, but I'm not sure it's a failing prescriptively.
Thanks for writing this up! It's really too bad that we couldn't do better than Pareto optimal. (I also think this is mathematically the same as Harsanyi, this writeup worked better for me.)
It's really too bad that we couldn't do better than Pareto optimal.
It seems like that's to be expected: ) is a polytope, and any Pareto optimal point will be an extreme point of that polytope. For each extreme point of the polytope, there exists some some linear objective function that is maximized over
) at that point. It remains to show that all the weights are non-negative, but that's taken care of by restricting your attention to the Pareto optimal points, and I suspect that any extreme point that's maximized by a non-negative utility function is Pareto optimal.
We also gain a lot by considering any convex combination of two policies as its own policy; the meat of the conclusion is "you should be willing to make linear tradeoffs between the decision-theoretic utility components of your aggregated decision-theoretic utility function," which is much cleaner with policy convexity than without it.
Restatement of: If you don't know the name of the game, just tell me what I mean to you. Alternative to: Why you must maximize expected utility. Related to: Harsanyi's Social Aggregation Theorem.
Summary: This article describes a theorem, previously described by Stuart Armstrong, that tells you to maximize the expectation of a linear aggregation of your values. Unlike the von Neumann-Morgenstern theorem, this theorem gives you a reason to behave rationally.1
The von Neumann-Morgenstern theorem is great, but it is descriptive rather than prescriptive. It tells you that if you obey four axioms, then you are an optimizer. (Let us call an "optimizer" any agent that always chooses an action that maximizes the expected value of some function of outcomes.) But you are a human and you don't obey the axioms; the VNM theorem doesn't say anything about you.
There are Dutch-book theorems that give us reason to want to obey the four VNM axioms: E.g., if we violate the axiom of transitivity, then we can be money-pumped, and we don't want that; therefore we shouldn't want to violate the axiom of transitivity. The VNM theorem is somewhat helpful here: It tells us that the only way to obey the four axioms is to be an optimizer.2
So now you have a reason to become an optimizer. But there are an infinitude of decision-theoretic utility functions3 to adopt — which, if any, ought you adopt? And there is an even bigger problem: If you are not already an optimizer, than any utility function that you're considering will recommend actions that run counter to your preferences!
To give a silly example, suppose you'd rather be an astronaut when you grow up than a mermaid, and you'd rather be a dinosaur than an astronaut, and you'd rather be a mermaid than a dinosaur. You have circular preferences. There's a decision-theoretic utility function that says
$\mbox{mermaid} \prec \mbox{astronaut} \prec \mbox{dinosaur}$which preserves some of your preferences, but if you have to choose between being a mermaid and being a dinosaur, it will tell you to become a dinosaur, even though you really really want to choose the mermaid. There's another decision-theoretic utility function that will tell you to pass up being a dinosaur in favor of being an astronaut even though you really really don't want to. Not being an optimizer means that any rational decision theory will tell you to do things you don't want to do.
So why would you ever want to be an optimizer? What theorem could possibly convince you to become one?
Stuart Armstrong's theorem
Suppose there is a set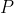 (for "policies") and some functions
(for "policies") and some functions 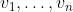 ("values") from
("values") from 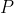 to
to 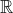 . We want these functions to satisfy the following convexity property:
. We want these functions to satisfy the following convexity property:
For any policies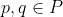 and any
and any 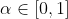 , there is a policy
, there is a policy 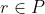 such that for all
such that for all 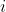 , we have
, we have  = \alpha v_i(p) + (1 - \alpha) v_i(q)) .
.
For policies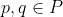 , say that
, say that 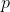 is a Pareto improvement over
is a Pareto improvement over 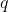 if for all
if for all  , we have
, we have  \geq v_i(q)) . Say that it is a strong Pareto improvement if in addition there is some
. Say that it is a strong Pareto improvement if in addition there is some 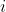 for which
for which  > v_i(q)) . Call
. Call 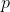 a Pareto optimum if no policy is a strong Pareto improvement over it.
a Pareto optimum if no policy is a strong Pareto improvement over it.
Theorem. Suppose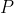 and
and 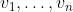 satisfy the convexity property. If a policy in
satisfy the convexity property. If a policy in 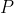 is a Pareto optimum, then it is a maximum of the function
is a Pareto optimum, then it is a maximum of the function 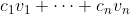 for some nonnegative constants
for some nonnegative constants 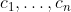 .
.
This theorem previously appeared in If you don't know the name of the game, just tell me what I mean to you. I don't know whether there is a source prior to that post that uses the hyperplane separation theorem to justify being an optimizer. The proof is basically the same as the proof for the complete class theorem and the hyperplane separation theorem and the second fundamental theorem of welfare economics. Harsanyi's utilitarian theorem has a similar conclusion, but it assumes that you already have a decision-theoretic utility function. The second fundamental theorem of welfare economics is virtually the same theorem, but it's interpreted in a different way.
What does the theorem mean?
Suppose you are a consequentialist who subscribes to Bayesian epistemology. And in violation of the VNM axioms, you are torn between multiple incompatible decision-theoretic utility functions. Suppose you can list all the things you care about, and the list looks like this:
Suppose further that you can quantify each item on that list with a function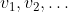 from world-histories to real numbers, and you want to optimize for each function, all other things being equal. E.g.,
from world-histories to real numbers, and you want to optimize for each function, all other things being equal. E.g., ) is large if
is large if 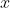 is a world-history where your welfare is great; and
is a world-history where your welfare is great; and ) somehow counts up the welfare of all mammals in world-history
somehow counts up the welfare of all mammals in world-history 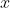 . If the expected value of
. If the expected value of 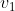 is at stake (but none of the other values are at stake), then you want to act so as to maximize the expected value of
is at stake (but none of the other values are at stake), then you want to act so as to maximize the expected value of 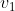 .4 And if only
.4 And if only 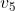 is at stake, you want to act so as to maximize the expected value of
is at stake, you want to act so as to maximize the expected value of 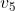 . What I've said so far doesn't specify what you do when you're forced to trade off value 1 against value 5.
. What I've said so far doesn't specify what you do when you're forced to trade off value 1 against value 5.
If you're VNM-rational, then you are an optimizer whose decision-theoretic utility function is a linear aggregation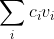 of your values and you just optimize for that function. (The
of your values and you just optimize for that function. (The 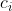 are nonnegative constants.) But suppose you make decisions in a way that does not optimize for any such aggregation.
are nonnegative constants.) But suppose you make decisions in a way that does not optimize for any such aggregation.
You will make many decisions throughout your life, depending on the observations you make and on random chance. If you're capable of making precommitments and we don't worry about computational difficulties, it is as if today you get to choose a policy for the rest of your life that specifies a distribution of actions for each sequence of observations you can make.5 Let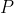 be the set of all possible policies. If
be the set of all possible policies. If 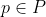 , and for any
, and for any 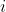 , let us say that
, let us say that ) is the expected value of
is the expected value of 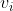 given that we adopt policy
given that we adopt policy 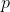 . Let's assume that these expected values are all finite. Note that if
. Let's assume that these expected values are all finite. Note that if 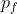 is a policy where you make every decision by maximizing a decision-theoretic utility function
is a policy where you make every decision by maximizing a decision-theoretic utility function 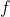 , then the policy
, then the policy 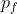 itself maximizes the expected value of
itself maximizes the expected value of 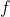 , compared to other policies.
, compared to other policies.
In order to apply the theorem, we must check that the convexity property holds. That's easy: If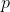 and
and 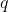 are two policies and
are two policies and 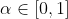 , the mixed policy where today you randomly choose policy
, the mixed policy where today you randomly choose policy 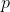 with probability
with probability 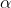 and policy
and policy 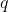 with probability
with probability 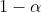 , is also a policy.
, is also a policy.
What the theorem says is that if you really care about the values on that list (and the other assumptions in this post hold), then there are linear aggregations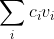 that you have reason to start optimizing for. That is, there are a set of linear aggregations and if you choose one of them and start optimizing for it, you will get more expected welfare for yourself, more expected welfare for others, less risk of the fall of civilization, ....
that you have reason to start optimizing for. That is, there are a set of linear aggregations and if you choose one of them and start optimizing for it, you will get more expected welfare for yourself, more expected welfare for others, less risk of the fall of civilization, ....
Adopting one of these decision-theoretic utility functions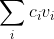 in the sense that doing so will get you more of the things you value without sacrificing any of them.
in the sense that doing so will get you more of the things you value without sacrificing any of them.
What's more, once you've chosen a linear aggregation, optimizing for it is easy. The ratio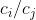 is a price at which you should be willing to trade off value
is a price at which you should be willing to trade off value 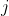 against value
against value 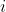 . E.g., a particular hour of your time should be worth some number of marginal dollars to you.
. E.g., a particular hour of your time should be worth some number of marginal dollars to you.
Addendum: Wei_Dai and other commenters point out that the set of decision-theoretic utility functions that will Pareto dominate your current policy very much depends on your beliefs. So a policy that seems Pareto dominant today will not have seemed Pareto dominant yesterday. It's not clear if you should use your current (posterior) beliefs for this purpose or your past (prior) beliefs.
More applications
There's a lot more that could be said about the applications of this theorem. Each of the following bullet points could be expanded into a post of its own:
1This post evolved out of discussions with Andrew Critch and Julia Galef. They are not responsible for any deficiencies in the content of this post. The theorem appeared previously in Stuart Armstrong's post If you don't know the name of the game, just tell me what I mean to you.
2That is, the VNM theorem says that being an optimizer is necessary for obeying the axioms. The easier-to-prove converse of the VNM theorem says that being an optimizer is sufficient.
3Decision-theoretic utility functions are completely unrelated to hedonistic utilitarianism.
4More specifically, if you have to choose between a bunch of actions and for all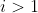 the expected value of
the expected value of 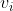 is independent of which actions you take, then you'll choose an action that maximizes the expected value of
is independent of which actions you take, then you'll choose an action that maximizes the expected value of 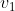 .
.
5We could formalize this by saying that for each sequence of observations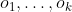 , the policy determines a distribution over the possible actions at time
, the policy determines a distribution over the possible actions at time 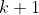 .
.