Epistemic status: not sure what to make of it.

Previously I had suggested that the laws of physics were the observers' attempts to make sense of the universe without laws while looking for patterns, which then become their models of reality. Some people suggested that this idea matched their intuition, others were bringing up Tegmark's mathematical universe as something that inherently has laws in it. Not being a fan of Tegmark (that's a different discussion) I will not pursue this avenue. Returning to the questions I have asked in the previous post, the first one was:

Can one start with a sequence of random numbers as a toy universe, i.e. no order and get somewhere that way, just by finding spurious patterns in the sequence?

This post attempts to create a toy model that does just that! it might appear contrived, but hopefully will make a bit of sense.
So, let's have our toy model of the universe as a sequence of random numbers. For definiteness, let's start with a uniform random sequence with elements between zero and one. While it is possible to get more random than that, it would require some effort. So, here is a sample sequence:

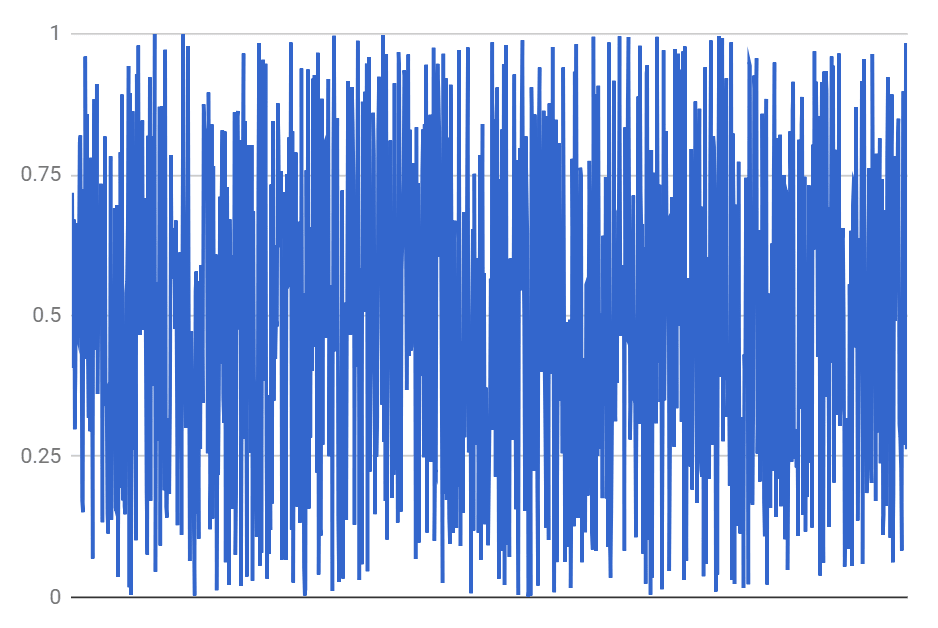
This looks, appropriately, rather orderless. One can see that this is so by looking at the power spectrum of this sequence. I have averaged about 10,000 of power spectra to get a smooth curve:

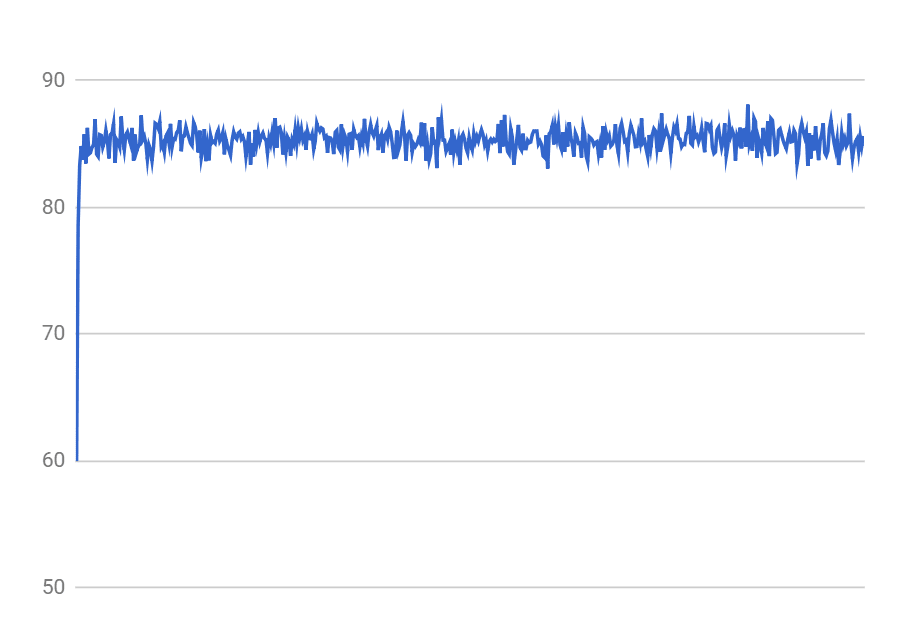
There are no correlations in this sequence and the power spectrum is flat, indicating the lack of order, as it should be. The random sequence was our toy universe, with the element (sample) number interpreted as the discrete "time" in this universe, t=1..1024.

But why let the time match the sample number? What is time, anyway? That has been, well, a timeless question for several thousands of years. Why do most of us, humans, perceive time as one-dimensional, inexorably going from the past to the future, and not in the other direction, or without any direction at all? A common answer to this question is related to the second law of thermodynamics:

The arrow of time matches the arrow of increasing entropy.

Well, not quite. The law, as generally formulated, states that entropy increases with time. But how do we know that this is a physical law and not a pattern we notice and successfully extrapolate, in keeping with the main thesis under consideration? Let's see what we can get from our toy model of a universe of random numbers. As remarked previously, the perceived passage of time is an open problem, so, until it is resolved, we are free to assign time values to our samples any way we wish.

Now comes the controversial part. 

How do we find something like entropy in this toy model? After all, there aren't any macrostates we can average over some microstates. The lack of order is intentionally built into this universe from the beginning. All we have is a bunch of numbers. So, let us use the magnitude of each number as a poor-man's proxy for entropy, and assign the later time to larger numbers. In other words, let's sort the random sequence! Here is a sample sorted sequence:

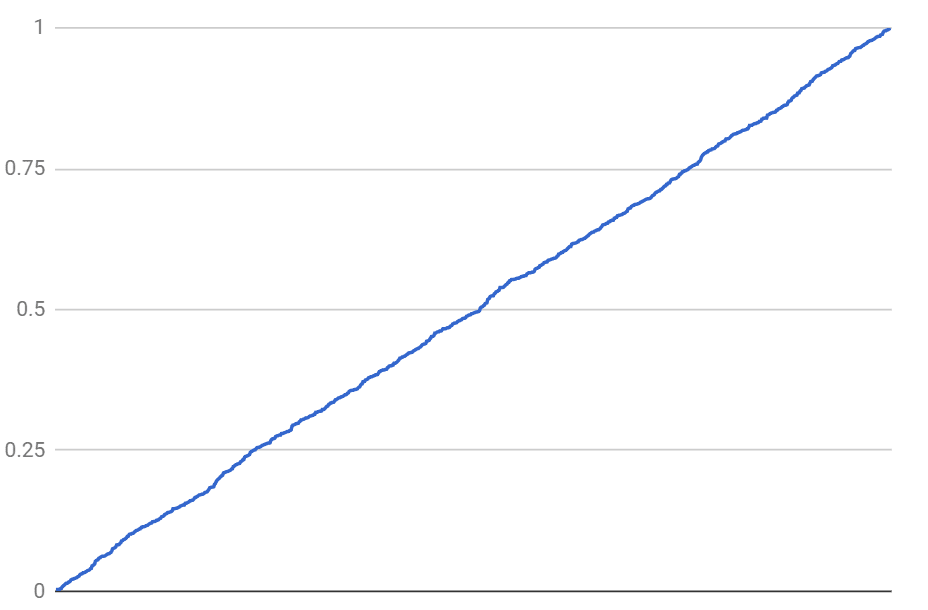
So, if we assign it in the ascending order, larger numbers corresponding to the later times, then, from the point of view of this hypothetical observer the universe would be quite predictable: the only quantity that exists in this universe monotonically increases with the perceived time.

In this ordered random universe an observer can definitely make at least one prediction, the same one we built into this ordering: that time goes forward. This is almost tautological. Let us try and see what other observables we can find here. One obvious thing to notice is that the line is not perfectly straight but has fluctuations. So let's subtract the trend and see what the fluctuations are like. Here is a picture for one run:

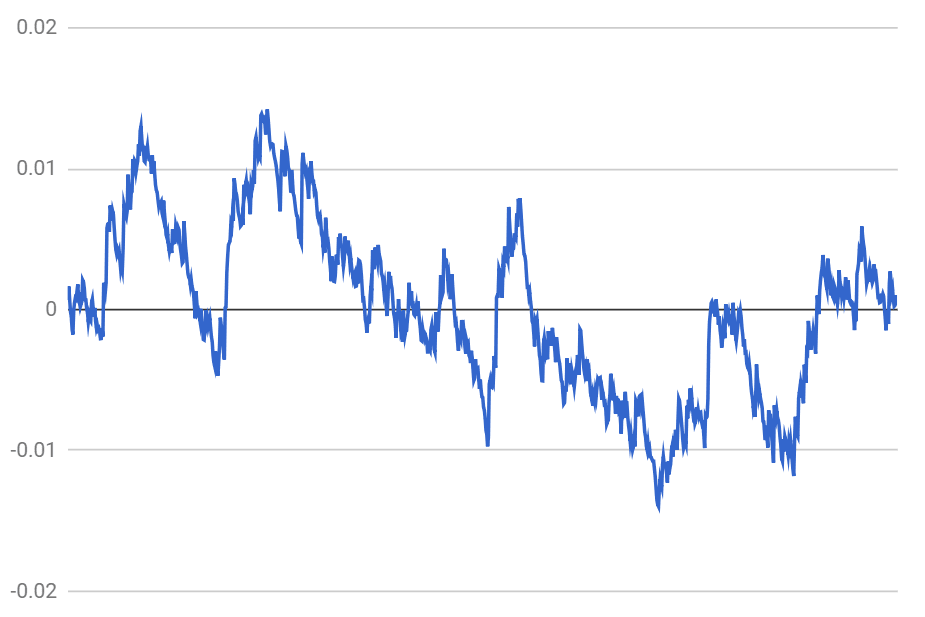
This is definitely not the uniform random noise anymore. To see what it is, let's look at the power spectrum again, averaged over 100,000 samples. I have included the power spectrum of the uniform distribution for comparison:

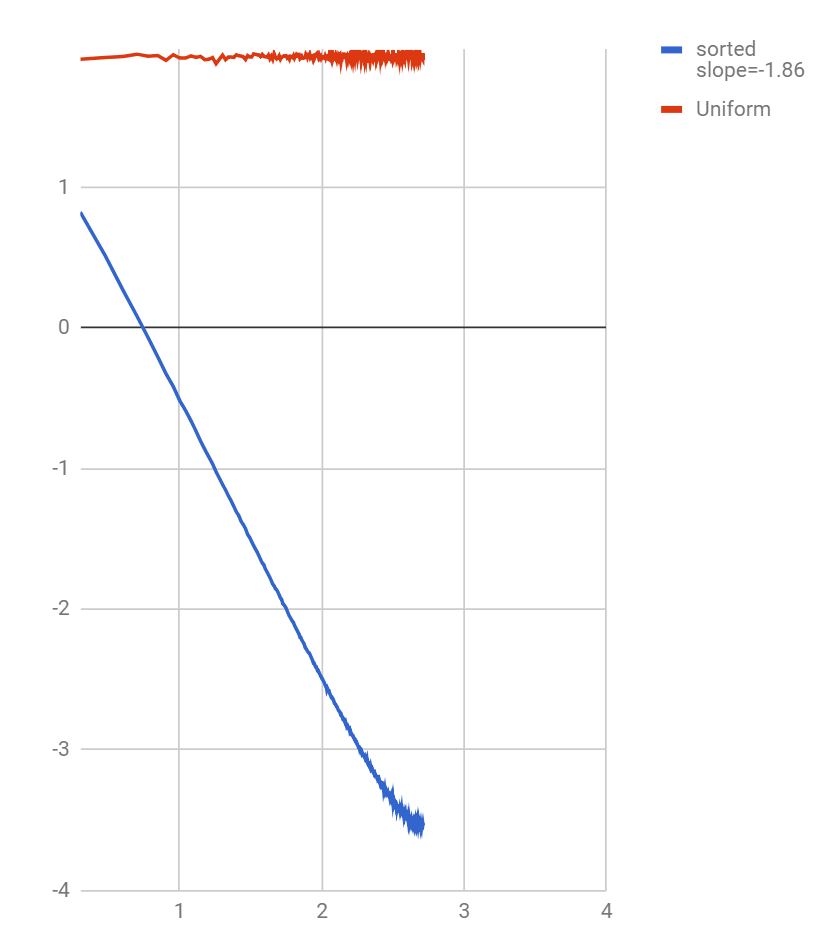
This is the log-log scale, as is customary for power spectra. The slope is non-integer, corresponding to the power law with the fractal dimension P~1/f^1.86. Initially I thought that this non-integer dimension could be an artifact of the random number generator being pseudo-random, but taking a "truly" random uniform distribution with the source of signal from actual physical noise did not materially change the outcome.  

If someone understands enough probability and statistics, and can explain what is going on here, please, by all means!

Now, let's take stock of what has happened: we started with uniformly distributed random noise, picked an "arrow of time", and ended up with fractal power-law fluctuations. Whether these fluctuations mimic an actual dynamical system, I am not sure, but if they do, this would mean creating apparent, if chaotic, order from randomness. 

I am not sure what this all might mean, if anything, so any feedback is welcome.