i don't think this metaphor makes things less confusing. i think the best way to understand this is just to directly understand the scaling laws. the chinchilla paper is an excellent reference (its main contribution is to fix a bug in the kaplan paper essentially; people have known since time immemorial that obviously amount of data matters in addition to model size).
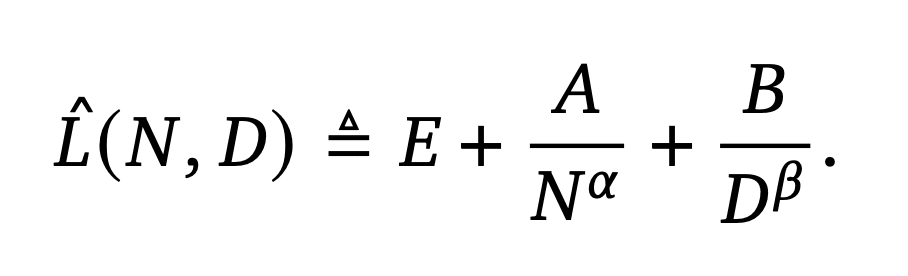
(N is parameter count, D is dataset size, L is loss)
for a fixed dataset, each model size has a best achievable loss with infinite data. if you train any longer, there is no capacity left. for each data size, there is also a best achievable loss with infinite model size. for a given training compute expenditure, there is an optimal tradeoff between training data and model size that achieves the best loss.
I think that Chinchilla provides a useful perspective for thinking about neural networks, it certainly turned my understanding on its head when it was published, but it is not the be-all-and-end-all of understanding neural network scaling.
The Chinchilla scaling laws are fairly specific to the supervised/self-supervised learning setup. As you mentioned, the key insight is that with a finite dataset, there's a point where adding more parameters doesn't help because you've extracted all the learnable signal from the data, or vice versa.
However, RL breaks that fixed-dataset assumption. For example, on-policy methods have a constantly shifting data distribution, so the concept of "dataset size" doesn't really apply.
There certainly are scaling laws for RL, they just aren't the ones presented in the Chinchilla paper. The intuition that compute allocation matters and different resources can bottleneck each other carries over, but the specifics can differ quite significantly.
And then there are evolutionary methods.
Personally, I find that the "parameters as pixels" analogy captures a more general intuition.
It's a good metaphor, but I think one important aspect this misses is overfitting - when you have a lot of parameters the NN can literally memorise small training sets till it gets 100% on the training set and 0% on the test set. Whereas a smaller model is forced to learn the underlying structure, so generalises better.
Hence larger models need a much larger training set even to match smaller models, which is another disadvantage of larger models (besides for higher per token training and inference costs).
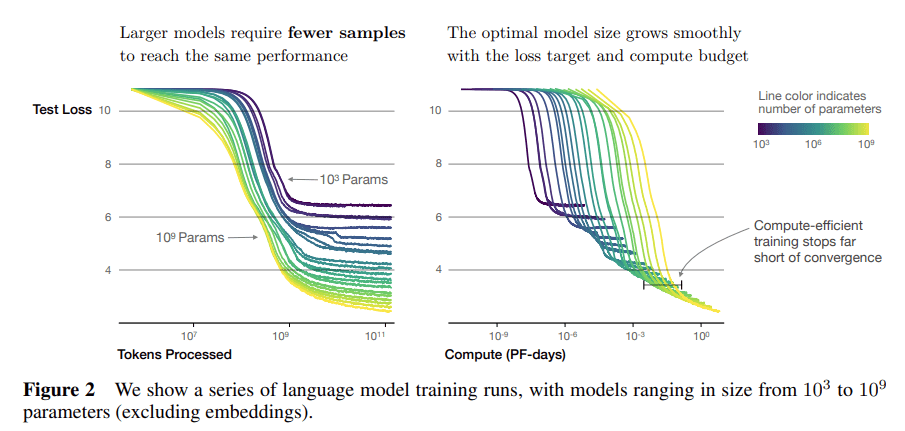
from https://arxiv.org/pdf/2001.08361
also see the grokking literature: https://en.wikipedia.org/wiki/Grokking_(machine_learning)
Previous discussion:
https://www.lesswrong.com/posts/FRv7ryoqtvSuqBxuT/understanding-deep-double-descent
larger models need a much larger training set even to match smaller models
This is empirically false, perplexity on a test set goes down with increase in model size even for a fixed dataset. See for example Figure 2 in the Llama 3 report, larger models do better with say 1e10 tokens on that plot.
Larger models could be said to want a larger dataset, in the sense that if you are training compute optimally, then with more compute you want both the model size and the dataset size to increase, and so the model size increases together with the dataset size. But even with the dataset of the same size they still do better, at least while reasonably close to compute optimal numbers of tokens.
This was the classical intuition, but turned out to be untrue in the regime of large NNs.
The modern view is double descent (https://en.wikipedia.org/wiki/Double_descent), where small models generalize better until the number of parameters exceeds the number of training examples, then larger models generalize better with the same amount of data.
More parameters = better model. So went the common misconception. After GPT-4.5, Llama 4, Nemotron-4, and many other "big models", I think most of you reading are already aware that the relationship between parameters and performance is not linear.
I think very few people actually have a solid intuition for what that relationship is like, though.
Chinchilla scaling laws proved that it's not just parameter count that matters, the amount of data does, too. Textbooks Are All You Need showed that data quality is actually really important. DoReMi told us that the mixture ratios between domains (code vs. web vs. books vs. math) are important. Mixture of Experts makes it plainly obvious that we can't even compare parameter count across architectures. And we haven't even touched on reinforcement learning...
Yet, there is some kind of relationship between parameter count and performance. The top left of that chart is empty.
Here's my intuition: neural network parameters are akin to pixels in an image. Images encode structure using pixels, neural nets encode structure using parameters.
More pixels/parameters means more room to encode larger and/or (at some tradeoff) more detailed structures. How you use that room is up to you.
A 100MP camera doesn't necessarily take better pictures than one with 10MP. If your lens sucks, your optics are miscalibrated, or you're just bad at framing an image, you're going to get bad results.
Pixels interact in unusual ways to create structure. If you configure them right you can get a dog, or a table, or a character, or an essay, or a diagram.
Parameters are even more versatile: while pixels have enforced local relationships (which can be replicated somewhat using convolutional networks), parameters can be connected however you like. Transformers represent a generalization of those relationships, letting parameters relate differently based on context.
Neural networks use parameters to create vast latent structures of complex, sometimes fuzzy circuits. Latent space is partitioned by each activation and the parameters are used to architect impossibly vast and intricate logical structures. The complexity of those structures is directly limited by the parameter count. You can try to fit more things into a limited amount of parameters the same way you can try to fit more things into a limited amount of pixels, but you trade off clarity until the network/image eventually becomes useless.
I think this is a good way to think about parameter counts. It explains why the focus has shifted towards total compute expenditure rather than "big model good". It gives you a frame for thinking about other machine learning concepts (if supervised learning is like taking a photograph of the dataset, what is RL?). And finally, it provides food for thought on some really interesting possibilities, like digital image editing suites for neural networks.