I ended up referring back to this post multiple times when trying to understand the empirical data on takeoff speeds and in-particular for trying to estimate the speed of algorithmic progress independent of hardware progress.
I also was quite interested in the details here in order to understand the absolute returns to more intelligence/compute in different domains.
One particular follow-up post I would love to see is to run the same study, but this time with material disadvantage. In-particular, I would really like to see, in both chess and go, how much material advantage AIs could make up for with greater intelligence/compute. This one seems particularly relevant for a bunch of takeoff dynamics in my current model of the world.
Very interesting, thanks!
- Could you confirm how much you have to scale down SF13 in order to match SF3? (This seems similar to what you did last time, but a more direct comparison.)
- The graph from last time makes it look like SF13 would match Rebel at about 20k nodes/move. Could you also confirm that?
- Looking forward to seeing the scaled-up Rebel results.
- With a baseline of 10 MNodes/move for SF3, I need to set SF13 to 0.375 MNodes/move for equality. That's a factor of 30. Caveat: I only ran 10 games which turned out equal, and only at 10 MNodes/move for SF3.
- Yes: Rebel6 at normal 2021 settings (40 moves in 15 min) can be approximately matched with SF13 at 20 kNodes/move. More precisely: I get parity between Rebel6 (128 MB) and SF13 (128 MB) for 16 MNodes/move vs. 20 kNodes/move (=factor of 800x). On my Intel Core-M 5Y31 (750 kNodes/s), that's 21s vs. 0.026s per move. Note that the figure shows SF8, not SF13.
- I was contacted by one person via PM, we are discussing the execution setup. Otherwise, I could do it by the end of July after my vacation.
I ran the experiment "Rebel 6 vs. Stockfish 13" on Amazon's AWS EC2. I rented a Xeon Platinum 8124M which benched at 18x 1.5 MNodes/s. I launched 18 concurrent single-threaded game sets with 128 MB of RAM for each engine. Again, ponder was of, no books, no tables. Time settings were 40 moves in 60s + 0.6 per move, corresponding to 17.5 MNodes/move. For reference, SF13 benches at ELO 3630 at this setting (entry "64 bit"); Rebel 6.0 got 2415 on a Pentium 90 (SSDF Computer Rating List (01-DEC-1996).txt, 90 kN/move).
The result:
- 1911 games played
- 18 draws
- No wins for Rebel
- All draws when Rebel played white
- ELO difference: 941 +- 63
Interpretation:
- Starting from 3630 for SF13, that corresponds to Rebel on a modern machine: 2689.
- Up from 2415, that's +274 ELO.
- The ELO gap between Rebel on a 1994 Pentium 90 (2415) and SF13 on a 2020 PC (3630) is 1215 points. Of these, 274 points are closed with matching hardware.
- That gives 23% for the compute, 77% for the algorithm.
Final questions:
- Isn't +274 ELO too little for 200x compute?
- We found 50% algo/50% compute for SF3-SF13. Why is that?
Answer: ELO gain with compute is not a linear function, but one with diminishing returns. Thus, the percentage "due to algo" increases, the longer the time frame. Thus, a fixed percentage is not a good answer.
But we can give the percentage as a function of time gap:
- Over 10 years, it's ~50%
- Over 25 years, it's ~22%
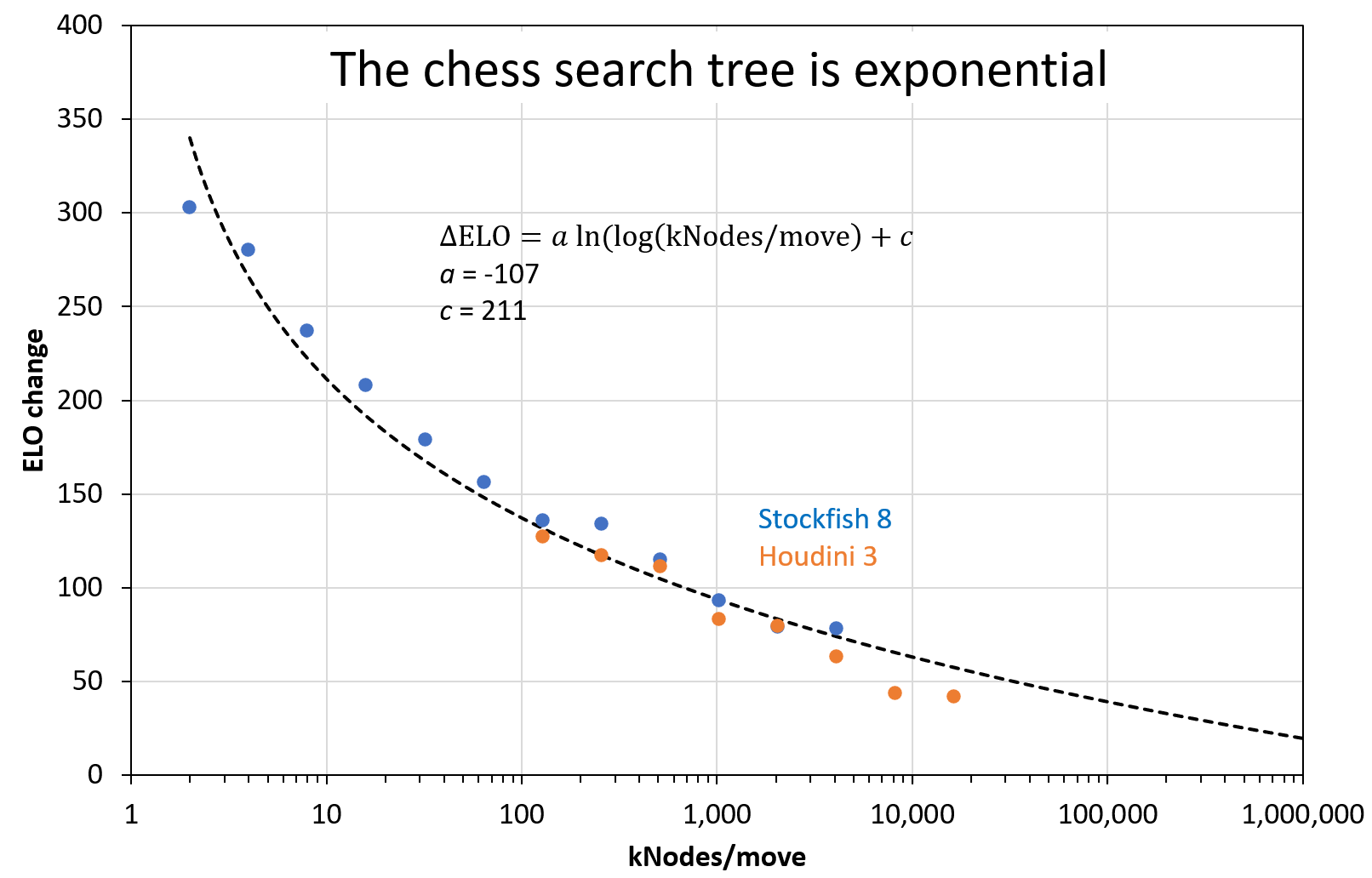
With data from other sources (SF8, Houdini 3) I made this figure to show the effect more clearly. The dashed black line is a double-log fit function: A base-10 log for the exponential increase of compute with time, and a natural log for the exponential search tree of chess. The parameter values are engine-dependent, but should be similar for engines of the same era (here: Houdini 3 and SF8). With more and more compute, the ELO gain approaches zero. In the future, we can expect engines whose curve is shifted to the right side of this plot.
I previously explored the performance of a modern chess engine on old hardware (1, 2). Paul Christiano asked for the case of an old engine running on modern hardware. This is the topic of the present post.
State of the art
Through an online search, I found the CCRL Blitz Rating list. It is run on an i7-4770k at 9.2 MNodes/s. The time controls are 2min+1s per move, i.e. 160s per 40 moves, or 4s per move. On the 4770k, that's 36.8 MNodes/move. The current number one on that list is Stockfish 14 at 3745 ELO. The list includes Fritz 5.32 from 1997, but on old hardware (Pentium 90. Over the years, CCRL moved through P90-P200-K62/450-Athlon1200-Athlon4600-4770k). I screened the list, but found no case of old-engine on modern hardware.
But the devil is in the details...
Making own experiments
In principle, the experiment should be trivial. The standard tool to compare chess engines is the command-line interface cutechess-cli. Set up old and new and get it running.
Problem 1: Find an old engine with a working interface
Paul and I independently favored the program Fritz from the most famous chess year 1997, because it was at the time well respected, had seen serious development effort over many years, and won competitions. The problem is that it only supports today's standard interface, UCI, since version 7 from the year 2001. So with that we can go back 20 years, but no more. Earlier versions used a proprietary interface (to connect to its GUI and to ChessBase), for which I found no converter.
I was then adviced by Stefan Pohl to try Rebel 6.0 instead. Rebel was amongst the strongest engines between 1980 and 2005. For example, it won the WCCC 1992 in Madrid. It was converted to UCI by its author Ed Schröder. I believe that old Rebel makes for a similarly good comparison as old Fritz.
A series of other old engines that support UCI are available for download. The following experiments should be possible with any of these.
Problem 2: Configuration
We can download Rebel 6 and set up cutechess like so:
One can define hash (RAM), pondering, and other settings through UCI in cutechess. However, Rebel does not accept these settings through the UCI interface. Instead, they must be defined in its config file wb2uci.eng:
The "wX" parameter sets hash/RAM: w0=2 MB, w1=4 MB,.. w9=512 MB
So, we can test RAM settings between 2 MB and 512 MB for the old engine. Stockfish is typically run at its default of 128 MB. That amount would have been possible on old machines (486 era), although it would have been not common.
For Rebel 6, the interface runs through an adaptor, which takes time. If we would ignore the fact, it would simply lose due to time control violations. So, we need to give it 1000ms of slack with "timemargin=1000". Now, let's go!
Problem 3: Measuring the quality of a player that losses every single game
I ran this experiment over night. The result after 1,000 matches? Stockfish won all of them. So it appears that Rebel is worse, but by how much? You can't tell if it loses almost every game.
Rebel 6.0 has ELO 2415 on a P90, Stockfish 13 is 3544 (SF14 is not in that list yet). That's a difference of 1129 ELO, with expectations to draw only one game in 2199; and lose the rest. Of course, Rebel 6 will have more than 2415 ELO when running on a modern machine - that's what we want to measure. Measuring the gap costs a lot of compute, because many games need to be played.
OK, can't we just make SF run slower until it is more equal? Sure, we can do that, but that's a different experiment: The one of my previous post. So, let's keep the time controls to something sensible, at least at Blitz level for SF. With time controls of 30s, a game takes about a minute. We expect to play for at most 2199 games (worth 36 hours) until the first draw occurs. If we want to collect 10 draws to fight small number statistics, that's worth 15 days of compute. On a 16-core machine, 1 day.
Unfortunately, I'm currently on vacation with no access to a good computer. If somebody out there has the resources to execute the experiment, let me know - happy to assist in setting it up!
Experiment: SF3 versus SF13
There is a similar experiment with less old software that can be done on smaller computers: Going back 8 years between new and old SF versions.
The Stockfish team self-tests new versions against old. This self-testing of Stockfish inflates the ELO score:
Let us compare these versions (SF3 vs SF13) more rigorously. The timegap between 2013 and 2021 is ~8 years. Let us choose a good, but not ridiculous computer for both epochs (something like <1000 USD for the CPU). That would buy us an Intel Core i7 4770K in 2013, and an AMD 5950X in 2021. Their SF multicore speed is 10 vs. 78 MN/s; a compute factor of 8x.
We can now test:
Answer: 32x (uncertainty: 30-35x)
Answer: 189 i.e. 50% of 379 ELO, or 30% of 631 ELO.
Interpretation: If we accept SF as amongst the very best chess programs in the last decade, we can make a more general assessment of chess compute vs. algorithm. Compute explains 30-50% of the computer chess ELO progress; algorithm improvements explain 50-70%.
Experiment method:
This runs a set of 100 rounds, changing colors each round, between SF3 and SF13 with their default parameters. The time controls in this example are 40 moves in 20 vs. 10 seconds etc. The time values must be explored in a wide range to determine consistency: The result may be valid for "fast" time controls, but not for longer games.
Minor influence factors
So far, we have used no pondering (default in cutechess), no endgame tables, no opening books, default RAM (128 MB for Stockfish).