This is so great, thanks for doing this! The more people internalize this stuff the better -- this is "raising the sanity waterline."
Is there a reason you use superscripts for potential outcomes, and not e.g. Y(a), or Y_a which I see a lot more often?
We define a “Confounder” as anything you need to introduce behind the conditioning sign of the exchangeability assumption, in order to make the assumption “true”.
A slight technicality is that a "confounder" refers to individual variables, while "confounding" refers to a ternary relation between sets. "Confounding"(A,Y,C) just means adjusting for C gives a valid functional for Y(a), that is conditional ignorability holds: Y(a) independent of A | C. "Confounder"(A,Y,c) (for a singleton c) means ???. It's not so simple -- seemingly reasonable definitions can fail. Tyler wrote a paper with me about this.
Fun exercise: what is the smallest DAG where the definition of a confounder contained in the first sentence on the Wikipedia article on confounding fails.
I think the number of upvotes should count as feedback, and you should put up the entire sequence (if for no other reason than a very handy online reference for future discussions on this topic, and as a way to bridge inference gaps). Causal stuff comes up a fair bit here, and it would be good if we could say "read article X in this sequence to understand what I mean."
edit: may add more later.
Thank you! I know that you will find a lot of errors in this sequence, so please point them out whenever you see them.
The reason for the superscript is that this was originally written for students in the epidemiology department at HSPH, where superscript is the standard notation due to Prof Hernan's book. I didn't want to change all the notation for the Less Wrong adaptation..
I am currently on my phone and will fix the definition of a confounder later tonight when I have access to a real computer. It is probably too early to give a definition before I introduce graphs
Edited to add: The simplest DAG where the definition in the first sentence of Wikipedia fails is when the suspected confounder is a mediator. I think the simplest example where the second definition on Wikipedia fails is M-bias. I will cover M-Bias in Part 3 of the sequence
I'm sorry that my reaction is relatively harsh. This is poorly written and very difficult to understand for someone who doesn't already know these basic topics.
It is possible to create arbitrarily complicated mathematical structures to describe empirical research. If the logic is done correctly, these structures are all completely valid, but they are only useful if the mathematical objects correctly represent the things in the real world that we want to learn about. Whenever someone tells you about a new framework which has been found to be mathematically valid, the first question you should ask yourself is whether the new framework allows you to correctly represent the important aspects of phenomena you are studying.
This is the first paragraph in your entire post, the one where you want to hook the reader and make them care about the subject, and you spend it on some sort of abstract verbiage that is not really relevant to the rest of the post. Imagine that your reader is someone who cannot name any "complicated mathematical structures" if you ask them to. What the hell are you talking about? What structures? What does "correctly represent" mean? What "new framework", what kind of framework are you talking about? Is "Riemannian manifolds" a "new framework"? Is "QFT" a "new framework"? And if it's so important to "ask yourself... whether allows... to correctly represent...", how do you answer this question? Maybe give an example of a "new framework" that DOESN'T allow this?
When we are interested in causal questions, the phenomenon we are studying is called "the data generating mechanism". The data generating mechanism is the causal force of nature that assigns value to variables. Questions about the data generating mechanism include “Which variable has its value assigned first?”, “What variables from the past are taken into consideration when nature assigns the value of a variable?” and “What is the causal effect of treatment”.
What does this MEAN? What kind of an entity is this "mechanism" supposed to be, hypothetical in your mind or physical? What does "assign" mean, what are "variables"? This fundamental (to your article) paragraph is so vague that it borders on mystical!
We can never observe the data generating mechanism. Instead, we observe something different, which we call “The joint distribution of observed variables”. The joint distribution is created when the data generating mechanism assigns value to variables in individuals. All questions about how whether observed variables are correlated or independent, and how about strongly they are correlated, are questions about the joint distribution.
You just lost all readers who don't know what a joint distribution is, including those who learned it at one time at school, remember that there is such a thing, but forgot what it is precisely. Additionally, in normal language you don't "observe variables", you MEASURE something. "Observe" means "stare hard" if you don't know the jargon. If someone knows the jargon, why do they need your basic explanation?
Look, I know this stuff enough for there not to be anything new for me in your article, and I still find it vexing when I read it. Why can't you give an example, or five? Like anything whatsoever... maybe a meteor in space flies close to a planet and gets captures by its gravitational field, or maybe your car goes off into a ditch because it slips on an icy road. Talk about how intuitively we perceive a cause-and-effect relationship and our physical theories back this up, but when we measure things, we just find a bunch of atoms (bodies, etc.) in space moving in some trajectory (or trajectories for many samples); the data we measure doesn't inherently include any cause-and-effect. Spend a few sentences on a particular example to make it sink in that data is just a bunch of numbers and that we need to do extra work, difficult work, to find "what causes what", and in particular this means understanding just what it means to say that. Then you can segue into counterfactuals, show how they apply to one or two examples from before, etc.
Thank you, this is important feedback. I'll think about whether it may be possible to incorporate it.
I know there are problems with the article, which is the reason I did not post to main. Part of the reason for publishing at all was to figure out how extensive the problems are, where readers get stuck etc. I tried to focus as much as possible on the issues that I got hung up on when I learned the material, but obviously this may differ from reader to reader. I understand that there may be parts of the theory that my mind glosses over, leading to a false sense of understanding. It is very helpful for me when people point it out.
I certainly invoke Crocker's Rule in order to get more accurate feedback.
I feel that I owe you a longer explanation of what I mean, especially in the light of a longish comment you wrote and then retracted (I thought it was fine, but nevermind). I invoke Crocker's Rule for myself, too.
I took another look the other day at your introduction paragraph, to better understand what was bugging me so much about it. Meanwhile you edited it down to this:
Whenever someone tells you about a new framework for describing empirical research, the first question you should ask yourself is whether the new framework allows you to correctly represent the important aspects of phenomena you are studying.
So here's the thing. The vagueness of this "empirical research" kept bugging me, and suddenly it dawned on me to try and see if this is a thing in epidemiology, which you said the article was originally rooted in. And turns out it is. Epidemiology journals, books etc. talk all the time about "empirical research" and "empirical research methods" etc. etc. As far as I could understand it - and I trust you'll correct me if I'm wrong - these refer to studies that collect relevant data about large numbers of people "in the wild" - perhaps cohorts, perhaps simply populations or subpopulations - and try to infer all kinds of stuff from the data. And this is contrasted with, for example, studying one particular person in a clinic, or studying how diseases spread on a molecular level, or other things one could do.
So, suddenly it's all very much clearer! I understand now what you were saying about complicated models etc. - you have a large dataset collected from a large population, you can do all kinds of complicated statistical/machine learning'y stuff with it, try to fit it to any number of increasingly complicated models and such, and you feel that while doing so, people often get lost in the complicated models, and you think causal inference is nice because it never loses track of things people on the ground actually want to know about the data, which tends to be stuff like "what causes what" or "what happens when I do this". Did I get this right?
OK, now consider this - I'm a computer programmer with a strong math background and strong interest in other natural sciences. I seem to be in the intended audience for your article - I deal with large datasets all the time and I'm very keen to understand causal inference better. When I see the phrase "empirical research", it doesn't tell me any of that stuff I just wrote. The closest phrase to this that I have in my normal vocabulary is "empirical sciences" which is really all natural sciences besides math. The only reasonable guess I have for "empirical research" is "things one finds out by actually studying something in the real world, and not just looking at the ceiling and thinking hard". So for example all of experimental physics comes under this notion of "empirical research", all chemistry done in a lab is "empirical research". All the OTHER kinds of epidemiological research that are NOT "empirical research" according to the way the phrase is used in epidemiology, I would still consider "empirical research" under this wide notion. Since the notion is so vague, I have no idea what kinds of "models" or "frameworks" to handle it you might possibly be thinking about. And it puzzles me that you even speak about something so wide and vague, and also it isn't clear what kinds of relevance it might have for causal inference anyway.
By now I spent probably x30 more time talking about that sentence than you spent writing it, but it's a symptom of a larger problem. You have a crisp and clear picture in your head: empirical research, that thing where you take N humans and record answers to K questions of interest for every one of them, and then try to see what this data can reveal. But when you put it into words, you fail to read those words with the simulated mind of your intended audience. Your intended audience in this case are not epidemiologists. They will not see the crisp and clear picture you get when you invoke the phrase "empirical research". It's on you to clearly understand that - that may be the most important thing you have to work on as an explainer of things to a non-specialist audience. But in your text this happens again and again. AND, to add to the problem, you DON'T use examples to make clear what you're talking about.
As a result, I spent upwards of 2 hours trying to understand just what two words in one sentence in your article mean. This is clearly suboptimal!
Now, I'll try to finish this already overlong comment quickly and point out several more examples of the same sort of problem in the article.
[in the next comment since this one is getting rejected as too long]
[cont'd from the parent comment]
1: when you first introduce "God's Table", it's really hard to understand what's going on, and the chief reason may be that you don't explicitly explain to the reader that the rows in the table are individuals for which you record the data. Again, this is something that's probably crystal clear to you, but I, the reader, at this point haven't seen any EXAMPLE of what you mean by "dataset", anything beyond vague talk of "observed variables". The rows in your table are only identified by "Id" of 1,2,3,4, which doesn't tell me anything useful, it can be just automatic numbering of rows. And since you have two variables of interest, A and Y, and four rows in the table, it's REALLY easy to just mistake the table for one which lists all possible combinations of values of A and Y and then adds more data dependent on those in the hypothetical columns you add. This interpretation of the table doesn't really make sense (the set of values is wrong for one thing) and it probably never occurred to you, but it took me a while to dig into your article and try to make sense of it to see that it doesn't make sense. It should be crystal clear to the reader on the first reading just what this table represents, and it just isn't. Again, if only you had a simple example running through the article! If only you wrote, I dunno, "John", "Mary", "Kim" and "Steven" as the row IDs to make it clear they were actual people, and "treatment" and "effect" (or better yet, "got better") instead of A and Y. It would have been so much easier to understand your meaning.
(then there're little things: why oh why do you write a=0 and a=1 in the conditioned variables instead of A=0, A=1? It just makes the reader wonder unhappily of there's some small-case 'a' they missed before in the exposition. "A" and "a" are normally two different variable names in math, even if they're not usually used together! Again, I need to spend a bunch of time to puzzle out that you really mean A=0 and A=1. And why A and Y anyway, if you call them treatment and effect, why not T and E? Why not make it easier on us? The little things)
2: You start a section with "What do we mean by Causality?" Then you NEVER ANSWER THIS. I reread this section three times just to make sure. Nope. You introduce counterfactual variables, God's table and then say "The goal of causal inference is to learn about God’s Table using information from the observed table (in combination with a priori causal knowledge)". I thought the goal of causal inference was to answer questions such as "what caused what". Sure, the link between the two may be very simple but it's a crucial piece of the puzzle and you explain more simple things elsewhere. You just explained what a "counterfactual" is to a person who possibly never heard the term before, so you can probably spare another two sentences (better yet, two sentences and an example!) on explaining just how we define causation via counterfactuals. If you title a section with the question "What do we mean by causality?" don't leave me guessing, ANSWER IT.
3: First you give a reasonably generic example of confounding and finish with "This is called confounding". Then later you call sex a confounder and helpfully add "We will give a definition of confounding in Part 2 of this sequence." OK, but what was the thing before then?
4: The A->L->Y thing. God, that's so confusing. At this point, again because there've been no examples, I have no clue what A,L,Y could conceivably stand for. Then you keep talking about "random functions" which to me are functions with random values; a "random function with a deterministic component dependent only on A" sounds like nonsense. "Probabilistic function" would be fine. "Random variable" would be fine if you assume basic knowledge in probability. "Random function" is just confusing but I took it to mean "probabilistic function".
Then you say "No matter how many people you sample, you cannot tell the graphs apart, because any joint distribution of L, A and Y that is consistent with graph 1, could also have been generated by graph 2".
Why?
It's obvious to you? It isn't obvious to me. I understand sort of vaguely why it might be true, and it certainly looks like a good demonstration of why joint distribution isn't enough, if it's true. Why is it true? The way you write seems like it should be the most obvious thing in the world to any reader. Well, it's not. Maybe if you had a running EXAMPLE (that probably sounds like a broken record by now)...
So I'm trying to puzzle this out. What if the values for A,L,Y are binary, and in the diagram on the left, L->A and L->Y always just copy values from L to those other two deterministically; while in the diagram on the left, let's say that A is always 1, L is randomly chosen to be 0 or 1 (so that its dependence on A is vacuous), while Y is a copy of L. Then the joint distribution generated by graph 1 will be, in order ALY, 100 or 111 with equal probability, and it cannot be generated by graph 2, because in any distribution generated by graph 2, A=Y in all samples.
Does that make sense, or did I miss something obvious? If I'm right, the example is wrong, and if I'm wrong, perhaps the example is not as crystal clear as it could have been, since it let me argue myself into such a mistake?
OK, how should I finish this. You may have gotten the impression from my previous comment that I was looking for a more rounded-off philosophical discussion of the relevant issues, but that's really not the case. My problem was not that you didn't spend 10 paragraphs on summarizing what we might mean by causality and what other approaches there are. It's fine to have a practical approach that goes straight to discussing data and what we do with it. The problem is that your article isn't readable by someone who isn't already familiar with the field. I feel that most of the problems could be solved by a combination of: a) a VERY careful rereading of the article from the p.o.v. of someone who's a subject-matter expert, but is completely ignorant of epidemiology, causal inference or any but the most basic notions in probability, and merciless rewriting/expanding of the text to make everything lucid for that hypothetical reader; b) adding a simple example that would run through the text and have every new definition or claim tested on it.
Thank you, this is very high-quality feedback, with a lot of clear advice on how I can improve the post. I will do my best to make improvements over the next few days. I greatly appreciate that you took the time to draw my attention to these things. Among many other things, you have convinced me that a lot of things about the set-up are not obvious to non-epidemiologists. The article may need extensive restructuring to fix this.
You are obviously completely right about my abuse of the term "empirical research". I will fix it to something like "observational correlation studies" tomorrow.
So I'm trying to puzzle this out. What if the values for A,L,Y are binary, and in the diagram on the left, L->A and L->Y always just copy values from L to those other two deterministically; while in the diagram on the left, let's say that A is always 1, L is randomly chosen to be 0 or 1 (so that its dependence on A is vacuous), while Y is a copy of L. Then the joint distribution generated by graph 1 will be, in order ALY, 100 or 111 with equal probability, and it cannot be generated by graph 2, because in any distribution generated by graph 2, A=Y in all samples.
I agree that this part of the post needs more work. I think what is happening, is that you have data on a probability distribution that was generated by graph 1, and are then asking if it could have been generated by a particular mechanism that can be described by graph 2. However, the point I wanted to make is that you would have been able to come up with some mechanism described by graph 2 that could account for the data.. I realize this is not clear, and I will work on it over the next few days.
why oh why do you write a=0 and a=1 in the conditioned variables instead of A=0, A=1?
When I use lower case a, I am referring to a specific value that the random variable A can take. Obviously, I agree that I should have spelled this out. For example , the counterfactual Y(a) describes would have happened we intervened to set A to a, where a can be either 0 or 1. The distinction between upper case and lower case is necessary..
However, the point I wanted to make is that you would have been able to come up with some mechanism described by graph 2 that could account for the data..
Thanks. I should have realized that, and I think I did at some point but later lost track of this. With this understood properly I can't think of any counterexample, and I feel more confident now that this is true, but I'm still not sure whether it ought to be obvious.
You just lost all readers who don't know what a joint distribution is
I think this is generally useful and fair feedback, but I don't think the above is quite fair, in the sense that people who don't know what a joint distribution is should not be reading this.
edit: Although, you know, I have to wonder. It is probably possible to teach causality without going into probability first. A computer program is a causal structure. When we stop program execution via a breakpoint and set a variable, that is an intervention. Computer programmers learn that stuff very early, and it is central to causality. It seems that the concepts end up being useful to statisticians and the like, not computer programmers, so probability theory gets put in early.
Anatoly, you mentioned earlier that you were looking for a readable intro to causal inference. I would be interested in what sorts of things you would be looking for in such an intro, in case I ever find the time to "write something."
Speaking as a high-school kid, I found the first two of your choice quotations entirely lucid. I have not yet read the article (don't ask why I'm in the comments before having done that), and so I would imagine that, the group of people that would a) find the writing style difficult, and b) wish to learn about causal inference in a mildly formal sense, have a very small overlap.
1) This is fantastic- I keep meaning to read more on how to actually apply Highly Advanced Epistemology to real data, and now I'm learning about it. Thanks!
2) This should be on Main.
3) Does there exist an alternative in the literature to the notation of Pr(A = a)? I hadn't realized until now how much the use of the equal sign there makes no sense. In standard usage, the equal sign either refers to literal equivalence (or isomorphism) as in functional programming, or variable assignment, as in imperative programming. This operation is obviously not literal equivalence (the set A is not equal to the element a), and it's only sort of like variable assignment. We do not erase our previous data of the set A: we want it to be around when we talk about observing other events from the set A.
In analogy with Pearl's "do" notation, I propose that we have an "observe notation", where Pr(A = a) would be written as Pr(obs_A (a)), and read as "probability that event a is observed from set A," and not overload our precious equal sign. (The overloading with equivalence vs. variable assignment is already stressful enough for the poor piece of notation.)
I'm not proposing that you change your notation for this sequence, but I feel like this notation might serve for clearer pedagogy in general.
I agree p(A = a) is imprecise.
Good notation for interventions has to permit easy nesting and conflicts for [ good reasons I don't want to get into right now ]. do(.) actually isn't very good for this reason (and I have deprecated it in my own work). I like various flavors of the potential outcome notation, e.g. Y(a) to mean "response Y under intervention do(a)". Ander uses Y^a (with a superscript) for the same thing.
With potential outcomes we can easily express things like "what would happen to Y if A were forced to a, and M were forced to whatever value M attained had A been instead forced to a' ": Y(a,M(a')). You can't even write this down with do(.).
The A=a notation always bugged me too. I like the above notation because it betrays morphism composition.
If we consider random variables as measure(able) spaces and conditional probabilities P(B | A) as stochastic maps B -> P(A), then every element 'a' of (a countably generated) A induces a point measure -> A giving probability 1 to that event. This is the map named by do(a). But since we're composing maps, not elements, we can use an element a unambiguously to mean its point measure. Then a series of measures separated by ',' give the product measure. In the above example, let a : A (implicitly, -> A), a' : B (implicitly, -> B), M : B ~> C, Y : (A,C) ~> D, then Y(a,M(a')) is a stochastic map ~> D given by composition
EDIT: How do I ascii art?
All of this is a fancy way of saying that "potential outcome" notation conveys exactly the right information to make probabilities behave nicely.
Yes, one of the reasons I am not very fond of subscript or superscript notation (that to be fair is very commonly used) is because it quickly becomes awkward to nest things, and I personally often end up nesting things many level deep. Parentheses is the only thing I found that works acceptably well.
If you think of interventions as a morphism, then it is indeed very natural to think in terms of arbitrary function composition, which leads one to the usual functional notation. The reason people in the causal inference community perhaps do not find this as natural as a mathematician would is because it is difficult to interpret things like Y(a,M(a')) as idealized experiments we could actually perform. There is a strong custom in the community (a healthy one in my opinion, because it grounds the discussion) to only consider quantities which can be so interpreted. See also this:
The "A=a" stands for the event that the random variable A takes on the value a. It's another notation for the set {ω ∈ Ω | A(ω) = a}, where Ω is your probability space and A is a random variable (a mapping from Ω to something else, often R^n).
Okay, maybe you know that, but I just want to point out that there is nothing vague about the "A=a" notation. It's entirely rigorous.
I think the grandparent refers to the fact that in the context of causality (not ordinary probability theory) there is a distinction between ordinary mathematical equality and imperative assignment. That is, when I write a structural equation model:
Y = f(A, M, epsilon(y))
M = g(A, epsilon(m))
A = h(epsilon(a))
and then I use p(A = a) or p(Y = y | do(A = a)) to talk about this model, one could imagine getting confused because the symbol "=" is used in two different ways. Especially for p(Y = y | do(A = a)). This is read as: "the probability of Y being equal to y given that I performed an imperative assignment on the variable A in the above three line program, and set it to value a." Both senses of "=" are used in the same expression -- it is quite confusing!
I really enjoyed this, and I agree that this belongs in Main. I think I'll need to read this a few more times before I understand this well. As I was reading this, I tried to fit these ideas in with other concepts I already had. I want to make sure that I am doing this in a way that makes sense, and in particular, that I am not missing any subtleties:
I'm imagining the 'data generating mechanism' as the computation that computed our joint distribution. To actually make inferences about this, you have to use some a priori causal information. To me, this looks a lot like Solomonoff induction - you are trying to find the most efficient computation that could have produced the joint distribution (i.e. 'Which variable was assigned first?' could be answered by 'Look at all the programs that could have computed the distribution, and find the most efficient/simplest one - your answer is whatever variable is assigned first in that program'). Does this sound right? Are there other aspects of the a priori causal information that this doesn't capture?
The positivity assumption is like saying that you have no prior knowledge of any (significant) differences between the two groups. For each given individual, your state of information as to which group they end up in is exactly the same. So using a coin with a known bias, or a perfectly deterministic pseudo random number generator are OK to use, and we can handle a 'random violation of positivity' just fine - but a structural violation is bad because either we did have some information, or our priors were really off. Does that sound about right?
Thanks!
re: 1: a data generating process is indeed a machine that produces the data we see. But, importantly, it also contains information about all sorts of other things, in particular what sort of data would come out had you given this machine completely different inputs. The fact that this machine encodes this sort of counterfactual information is what makes it "in the causal magisterium," so to speak.
The machine itself is presumed to be "out there." If we are trying to learn what that machine might be, we may wish to invoke assumptions akin to Occam's razor. But this is about us trying to learn something, not about the machine per se. Nature is not required to be convenient!
To use an analogy our mutual friend Judea likes to use, 'the joint distribution' is akin to encoding how some object, say a vase, reflects light from every angle. This information is sufficient to render this vase in a computer graphics system. But this information is not sufficient to render what happens if we smash a vase -- we need in addition to the surface information, also additional information about the material of the vase, how brittle it is, etc. The 'data generating process' would contain in addition to surface info about light reflectivity, also information that lets us deduce how a vase would react to any counterfactual deformation we might perform, whether we drop it from a table, or smash it with a hammer, or lightly nudge it.
Thanks for your reply.
At least the way I am conceiving a computation, I can (theoretically) run the same computation with different inputs. So I think a computation would capture that sort of counterfactual information also.
So in LW terms - beware of the mind projection fallacy.
Thank you!
I am not sure your understanding of positivity is right: It is simply a matter of whether there exists any stratum where nobody is treated (or nobody is untreated).
The distinction between "random" and "structural" violations was inherited from a course that did not insist as strongly on distinguishing between statistics and causal inference. I think the necessary assumption for identification is structural positivity, and that "random violation of positivity" is simply an apparent violation of the assumption due to sampling. I will update the text to make this clear.
I'll keep thinking about your question 1. Possibly there are other people who would be better suited to answer it than me..
I'm not an expert on causal inference, and I'm having some trouble grasping what you mean by "data-generating mechanism". Intuitively, I would think that data is generated by a joint probability distribution, but you say that the "data-generating mechanism" is something different than the joint probability distribution and it actually generates it.
To test my understanding, I'll try to reformulate this in the language of standard (non-causal) probability theory:
The "data-generating mechanism" is a stochastic process that jointly generates all your observed data. It can have inputs (that is, it can be a channel), it can be non-stationary, and so on.
The data that is generated can be broken into individual samples (e.g. patients). Under certain assumptions, it can be considered that these samples were independently sampled from a memory-less, input-less probability distribution, which is what you call the "joint probability distribution" (it is joint on the variables within each samples, but not on the samples themselves).
We are interested in estimating the "data-generating mechanism" from the observed data. Since this is a difficult task, we break it into two sub-tasks: biostatistics, which consists in estimating the per-sample joint probability distribution, and epidemiology, which consists in estimating the whole stochastic process from this per-sample distribution.
Is my summary correct?
Thanks for the comment! I am not confident in answering whether your summary is correct or not, partly because it looks like we come from different backgrounds which use different languages to describe the same things.
The point I am trying to make is that the joint distribution of A, B and C only consists of information such as "in 15% of the population, A=1, B=1 and C=1, in 5% of the population A=0, B=1 and C=1" etc
If the data was generated by a joint distribution, this seems like it would be something like an algorithm that just says "Assign 'A=1, B=1, C=1' with probability 0.15 and assign 'A=0, B=1, C=1' with probability 0.05" etc
However, for causal inference, it is necessary to model the world as if the joint distribution is generated by three separate algorithms: One for A, one for B and one for C. There are many possible sets of such algorithms that will result in the same joint distribution.
We will therefore need to set up the problem so that we explicitly state the order in which the variables are generated, and stipulate that the input can consist only of variables from the past.
(Part 1 of the Sequence on Applied Causal Inference)
In this sequence, I am going to present a theory on how we can learn about causal effects using observational data. As an example, we will imagine that you have collected information on a large number of Swedes - let us call them Sven, Olof, Göran, Gustaf, Annica, Lill-Babs, Elsa and Astrid. For every Swede, you have recorded data on their gender, whether they smoked or not, and on whether they got cancer during the 10-years of follow-up. Your goal is to use this dataset to figure out whether smoking causes cancer.
We are going to use the letter A as a random variable to represent whether they smoked. A can take the value 0 (did not smoke) or 1 (smoked). When we need to talk about the specific values that A can take, we sometimes use lower case a as a placeholder for 0 or 1. We use the letter Y as a random variable that represents whether they got cancer, and L to represent their gender.
The data-generating mechanism and the joint distribution of variables
Imagine you are looking at this data set:
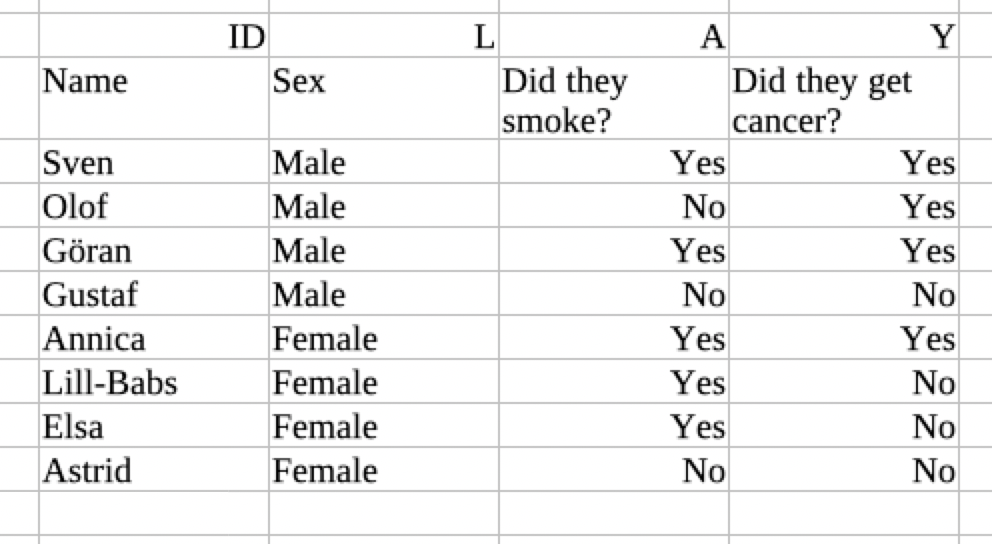
This table records information about the joint distribution of the variables L, A and Y. By looking at it, you can tell that 1/4 of the Swedes were men who smoked and got cancer, 1/8 were men who did not smoke and got cancer, 1/8 were men who did not smoke and did not get cancer etc.
You can make all sorts of statistics that summarize aspects of the joint distribution. One such statistic is the correlation between two variables. If "sex" is correlated with "smoking", it means that if you know somebody's sex, this gives you information that makes it easier to predict whether they smoke. If knowing about an individual's sex gives no information about whether they smoked, we say that sex and smoking are independent. We use the symbol ∐ to mean independence.
When we are interested in causal effects, we are asking what would happen to the joint distribution if we intervened to change the value of a variable. For example, how many Swedes would get cancer in a hypothetical world where you intervened to make sure they all quit smoking?
In order to answer this, we have to ask questions about the data generating mechanism. The data generating mechanism is the algorithm that assigns value to the variables, and therefore creates the joint distribution. We will think of the data as being generated by three different algorithms: One for L, one for A and one for Y. Each of these algorithms takes the previously assigned variables as input, and then outputs a value.
Questions about the data generating mechanism include “Which variable has its value assigned first?”, “Which variables from the past (observed or unobserved) are used as inputs” and “If I change whether someone smokes, how will that change propagate to other variables that have their value assigned later". The last of these questions can be rephrased as "What is the causal effect of smoking”.
The basic problem of causal inference is that the relationship between the set of possible data generating mechanisms, and the joint distribution of variables, is many-to-one: For any correlation you observe in the dataset, there are many possible sets of algorithms for L, A and Y that could all account for the observed patterns. For example, if you are looking at a correlation between cancer and smoking, you can tell a story about cancer causing people to take up smoking, or a story about smoking causing people to get cancer, or a story about smoking and cancer sharing a common cause.
An important thing to note is that even if you have data on absolutely everyone, you still would not be able to distinguish between the possible data generating mechanisms. The problem is not that you have a limited sample. This is therefore not a statistical problem. What you need to answer the question, is not more people in your study, but a priori causal information. The purpose of this sequence is to show you how to reason about what prior causal information is necessary, and how to analyze the data if you have measured all the necessary variables.
Counterfactual Variables and "God's Table":
The first step of causal inference is to translate the English language research question «What is the causal effect of smoking» into a precise, mathematical language. One possible such language is based on counterfactual variables. These counterfactual variables allow us to encode the concept of “what would have happened if, possibly contrary to fact, the person smoked”.
We define one counterfactual variable called Ya=1 which represents the outcome in the person if he smoked, and another counterfactual variable called Ya=0 which represents the outcome if he did not smoke. Counterfactual variables such as Ya=0 are mathematical objects that represent part of the data generating mechanism: The variable tells us what value the mechanism would assign to Y, if we intervened to make sure the person did not smoke. These variables are columns in an imagined dataset that we sometimes call “God’s Table”:
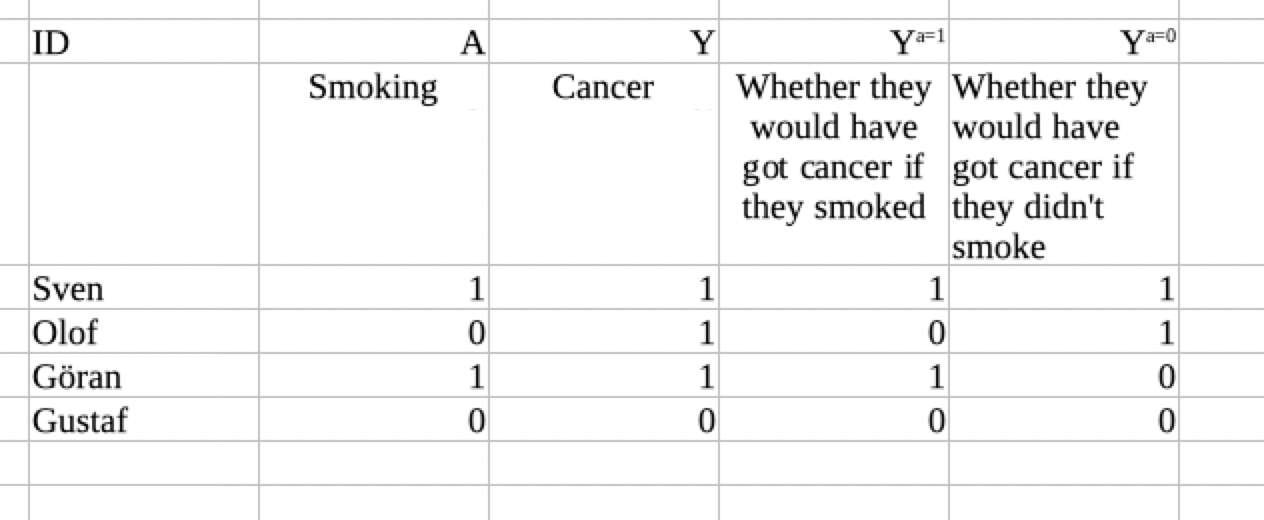
Let us start by making some points about this dataset. First, note that the counterfactual variables are variables just like any other column in the spreadsheet. Therefore, we can use the same type of logic that we use for any other variables. Second, note that in our framework, counterfactual variables are pre-treatment variables: They are determined long before treatment is assigned. The effect of treatment is simply to determine whether we see Ya=0 or Ya=1 in this individual.
If you had access to God's Table, you would immediately be able to look up the average causal effect, by comparing the column Ya=1 to the column Ya=0. However, the most important point about God’s Table is that we cannot observe Ya=1 and Ya=0. We only observe the joint distribution of observed variables, which we can call the “Observed Table”:
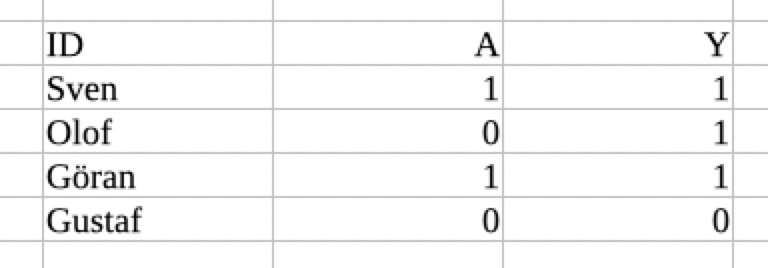
The goal of causal inference is to learn about God’s Table using information from the observed table (in combination with a priori causal knowledge). In particular, we are going to be interested in learning about the distributions of Ya=1 and Ya=0, and in how they relate to each other.
Randomized Trials
The “Gold Standard” for estimating the causal effect, is to run a randomized controlled trial where we randomly assign the value of A. This study design works because you select one random subset of the study population where you observe Ya=0, and another random subset where you observe Ya=1. You therefore have unbiased information about the distribution of both Ya=0 and of Ya=1.
An important thing to point out at this stage is that it is not necessary to use an unbiased coin to assign treatment, as long as your use the same coin for everyone. For instance, the probability of being randomized to A=1 can be 2/3. You will still see randomly selected subsets of the distribution of both Ya=0 and Ya=1, you will just have a larger number of people where you see Ya=1. Usually, randomized trials use unbiased coins, but this is simply done because it increases the statistical power.
Also note that it is possible to run two different randomized controlled trials: One in men, and another in women. The first trial will give you an unbiased estimate of the effect in men, and the second trial will give you an unbiased estimate of the effect in women. If both trials used the same coin, you could think of them as really being one trial. However, if the two trials used different coins, and you pooled them into the same database, your analysis would have to account for the fact that in reality, there were two trials. If you don’t account for this, the results will be biased. This is called “confounding”. As long as you account for the fact that there really were two trials, you can still recover an estimate of the population average causal effect. This is called “Controlling for Confounding”.
In general, causal inference works by specifying a model that says the data came from a complex trial, ie, one where nature assigned a biased coin depending on the observed past. For such a trial, there will exist a valid way to recover the overall causal results, but it will require us to think carefully about what the correct analysis is.
Assumptions of Causal Inference
We will now go through in some more detail about why it is that randomized trials work, ie , the important aspects of this study design that allow us to infer causal relationships, or facts about God’s Table, using information about the joint distribution of observed variables.
We will start with an “observed table” and build towards “reconstructing” parts of God’s Table. To do this, we will need three assumptions: These are positivity, consistency and (conditional) exchangeability:
Positivity
Positivity is the assumption that any individual has a positive probability of receiving all values of the treatment variable: Pr(A=a) > 0 for all values of a. In other words, you need to have both people who smoke, and people who don't smoke. If positivity does not hold, you will not have any information about the distribution of Ya for that value of a, and will therefore not be able to make inferences about it.
We can check whether this assumption holds in the sample, by checking whether there are people who are treated and people who are untreated. If you observe that in any stratum, there are individuals who are treated and individuals who are untreated, you know that positivity holds.
If we observe a stratum where no individuals are treated (or no individuals are untreated), this can be either for statistical reasons (your randomly did not sample them) or for structural reasons (individuals with these covariates are deterministically never treated). As we will see later, our models can handle random violations, but not structural violations.
In a randomized controlled trial, positivity holds because you will use a coin that has a positive probability of assigning people to either arm of the trial.
Consistency
The next assumption we are going to make is that if an individual happens to have treatment (A=1), we will observe the counterfactual variable Ya=1 in this individual. This is the observed table after we make the consistency assumption:
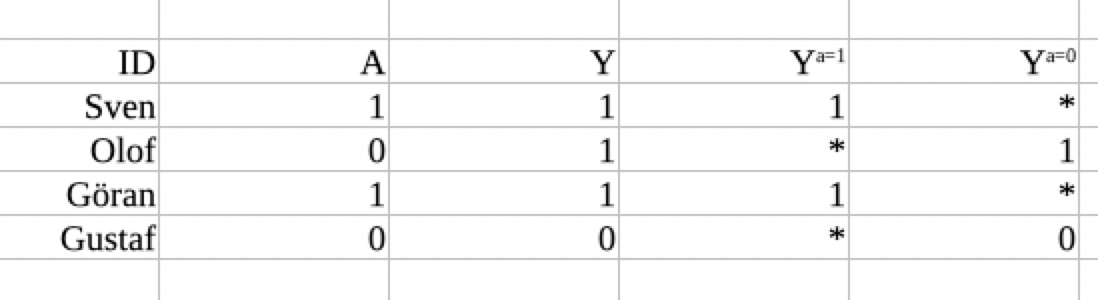
Making the consistency assumption got us half the way to our goal. We now have a lot of information about Ya=1 and Ya=0. However, half of the data is still missing.
Although consistency seems obvious, it is an assumption, not something that is true by definition. We can expect the consistency assumption to hold if we have a well-defined intervention (ie, the intervention is a well-defined choice, not an attribute of the individual), and there is no causal interference (one individual’s outcome is not affected by whether another individual was treated).
Consistency may not hold if you have an intervention that is not well-defined: For example, there may be multiple types of cigarettes. When you measure Ya=1 in people who smoked, it will actually be a composite of multiple counterfactual variables: One for people who smoked regular cigarettes (let us call that Ya=1*) and another for people who smoked e-cigarettes (let us call that Ya=1#). Since you failed to specify whether you are interested in the effect of regular cigarettes or e-cigarettes, the construct Ya=1 is a composite without any meaning, and people will be unable to use your results to predict the consequences of their actions.
Exchangeability
To complete the table, we require an additional assumption on the nature of the data. We call this assumption “Exchangeability”. One possible exchangeability assumption is “Ya=0 ∐ A and Ya=1 ∐ A”. This is the assumption that says “The data came from a randomized controlled trial”. If this assumption is true, you will observe a random subset of the distribution of Ya=0 in the group where A=0, and a random subset of the distribution of Ya=1 in the group where A=1.
Exchangeability is a statement about two variables being independent from each other. This means that having information about either one of the variables will not help you predict the value of the other. Sometimes, variables which are not independent are "conditionally independent". For example, it is possible that knowing somebody's genes helps you predict whether they enjoy eating Hakarl, an Icelandic form of rotting fish. However, it is also possible that these genes are just markers for whether a person was born in the ethnically homogenous Iceland. In such a situation, it is possible that once you already know whether somebody is from Iceland, also learning about their genes will gives you no additional clues as to whether they will enjoy Hakarl. If that is the case, the variables "genes" and "enjoying hakarl" are conditionally independent, given nationality.
The reason we care about conditional independence is that sometimes you may be unwilling to assume that marginal exchangeability Ya=1 ∐ A holds, but you are willing to assume conditional exchangeability Ya=1 ∐ A | L. In this example, let L be sex. The assumption then says that you can interpret the data as if it came from two different randomized controlled trials: One in men, and one in women. If that is the case, sex is a "confounder". (We will give a definition of confounding in Part 2 of this sequence. )
If the data came from two different randomized controlled trials, one possible approach is to analyze these trials separately. This is called “stratification”. Stratification gives you effect measures that are conditional on the confounders: You get one measure of the effect in men, and another in women. Unfortunately, in more complicated settings, stratification-based methods (including regression) are always biased. In those situations, it is necessary to focus the inference on the marginal distribution of Ya.
Identification
If marginal exchangeability holds (ie, if the data came from a marginally randomized trial), making inferences about the marginal distribution of Ya is easy: You can just estimate E[Ya] as E [Y|A=a].
However, if the data came from a conditionally randomized trial, we will need to think a little bit harder about how to say anything meaningful about E[Ya]. This process is the central idea of causal inference. We call it “identification”: The idea is to write an expression for the distribution of a counterfactual variable, purely in terms of observed variables. If we are able to do this, we have sufficient information to estimate causal effects just by looking at the relevant parts of the joint distribution of observed variables.
The simplest example of identification is standardization. As an example, we will show a simple proof:
Begin by using the law of total probability to factor out the confounder, in this case L:
· E(Ya) = Σ E(Ya|L= l) * Pr(L=l) (The summation sign is over l)
We do this because we know we need to introduce L behind the conditioning sign, in order to be able to use our exchangeability assumption in the next step: Then, because Ya ∐ A | L, we are allowed to introduce A=a behind the conditioning sign:
· E(Ya) = Σ E(Ya|A=a, L=l) * Pr(L=l)
Finally, use the consistency assumption: Because we are in the stratum where A=a in all individuals, we can replace Ya by Y
· E(Ya) = Σ E(Y|A=a, L=l) * Pr (L=l)
We now have an expression for the counterfactual in terms of quantities that can be observed in the real world, ie, in terms of the joint distribution of A, Y and L. In other words, we have linked the data generating mechanism with the joint distribution – we have “identified” E(Ya). We can therefore estimate E(Ya)
This identifying expression is valid if and only if L was the only confounder. If we had not observed sufficient variables to obtain conditional exchangeability, it would not be possible to identify the distribution of Ya : there would be intractable confounding.
Identification is the core concept of causal inference: It is what allows us to link the data generating mechanism to the joint distribution, to something that can be observed in the real world.
The difference between epidemiology and biostatistics
Many people see Epidemiology as «Applied Biostatistics». This is a misconception. In reality, epidemiology and biostatistics are completely different parts of the problem. To illustrate what is going on, consider this figure:
The data generating mechanism first creates a joint distribution of observed variables. Then, we sample from the joint distribution to obtain data. Biostatistics asks: If we have a sample, what can we learn about the joint distribution? Epidemiology asks: If we have all the information about the joint distribution , what can we learn about the data generating mechanism? This is a much harder problem, but it can still be analyzed with some rigor.
Epidemiology without Biostatistics is always impossible:.Since we cannot observe the infinitely many observations that make up the joint distribution, learning about it will always involves sampling. Therefore, we will need good statistical estimators of the joint distribution.
Biostatistics without Epidemiology is usually pointless: The joint distribution of observed variables is simply not interesting in itself. You can make the claim that randomized trials is an example of biostatistics without epidemiology. However, the epidemiology is still there. It is just not necessary to think about it, because the epidemiologic part of the analysis is trivial
Note that the word “bias” means different things in Epidemiology and Biostatistics. In Biostatistics, “bias” is a property of a statistical estimator: We talk about whether ŷ is a biased estimator of E(Y |A). If an estimator is biased, it means that when you use data from a sample to make inferences about the joint distribution in the population the sample came from, there will be a systematic source of error.
In Epidemiology, “bias” means that you are estimating the wrong thing: Epidemiological bias is a question about whether E(Y|A) is a valid identification of E(Ya). If there is epidemiologic bias, it means that you estimated something in the joint distribution, but that this something does not answer the question you were interested in.
These are completely different concepts. Both are important and can lead to your estimates being wrong. It is possible for a statistically valid estimator to be biased in the epidemiologic sense, and vice versa. For your results to be valid, your estimator must be unbiased in both senses.