Reflective consistency, randomized decisions, and the dangers of unrealistic thought experiments
2avturchin
5Radford Neal
2avturchin
4Radford Neal
2TAG
2Ape in the coat
5jessicata
1Ape in the coat
3Radford Neal
2Ape in the coat
3jessicata
3Radford Neal
1rotatingpaguro
1Radford Neal
2[comment deleted]
2Ape in the coat
1Radford Neal
1Ape in the coat
2Charlie Steiner
2Radford Neal
2Charlie Steiner
1Radford Neal
2Charlie Steiner
3Radford Neal
3Charlie Steiner
1dadadarren
New Comment
Reflexive inconsistency can manifest even in simpler decision theory experiments, such as the prisoner's dilemma. Before being imprisoned, anyone would agree that cooperation is the best course of action. However, once in jail, an individual may doubt whether the other party will cooperate and consequently choose to defect.
In the Newcomb paradox, reflexive inconsistency becomes even more central, as it is the very essence of the problem. At one moment, I sincerely commit to a particular choice, but in the next moment, I sincerely defect from that commitment. A similar phenomenon occurs in the Hitchhiker problem, where an individual makes a promise in one context but is tempted to break it when the context changes.
Well, I think the prisoner's dilemma and Hitchhiker problems are ones where some people just don't accept that defecting is the right decision. That is, defecting is the right decision if (a) you care nothing at all for the other person's welfare, (b) you care nothing for your reputation, or are certain that no one else will know what you did (including the person you are interacting with, if you ever encounter them again), and (c) you have no moral qualms about making a promise and then breaking it. I think the arguments about these problems amount to people saying that they are assuming (a), (b), and (c), but then objecting to the resulting conclusion because they aren't really willing to assume at least one of (a), (b), or (c).
Now, if you assume, contrary to actual reality, that the other prisoner or the driver in the Hitchhiker problem are somehow able to tell whether you are going to keep your promise or not, then we get to the same situation as in Newcomb's problem - in which the only "plausible" way they could make such a prediction is by creating a simulated copy of you and seeing what you do in the simulation. But then, you don't know whether you are the simulated or real version, so simple application of causal decision theory leads you keep your promise to cooperate or pay, since if you are the simulated copy that has a causal effect on the fate of the real you.
One might imagine “people” who are computer programs, which might be written to be deterministic, and so would perform exactly the same actions
I think you have hit the nail on the head there. Lesswrong has a habit of assuming determinism and computationalism where they are not givens.
You seem to be analysing a different problem, then assume that it means that you've solved the original problem.
Yes, if the bet is null and void when people failed to coordinate, probabilistic strtategy is very helpful to distinguish, between 18 people with green marbles and 2 people with green marbles as it's easier for two people to coordinate than for 18. But the point of the original problem is that you shouldn't be able to do it.
What if just one person with green marble agreeing to take the bet is enough? It's not some unrealistic mind experiment. Just a simple change to the betting scheme. And yet it immediately invalidates your clever probabilistic solution. Actually if you just kept the $50 penalty for discoordination condition, it wouldn't work as well.
Eliezer says 'We can try to help out the causal decision agents on their coordination problem by supplying rules such as "If conflicting answers are delivered, everyone loses $50"'.
But such coercion is not actually helpful. We can see this easily by simply negating the rewards in this problem
That doesn't follow. Reversed rewards is a completely different problem than non reversed rewards with $50 penalty for discoordination. Well done at analysing the case that you've analysed, but the probabilistic strategy predictably quite suboptimal in $50 penalty case.
If just one has to agree, then you should say "yes" a small percent of the time, because then it's more likely at least one says "yes" in the 18 case than the 2 case, because there are 18 chances. E.g. if you say yes 1% of the time then it's "yes" about 18% of the time in the 18 case and 2% in the 2 case which is worth it. I think when your policy is saying yes the optimal percent of the time, you're as a CDT individual indifferent between the two options (as implied by my CDT+SIA result). Given this indifference the mixed strategy is compatible with CDT rationality.
With the discoordination penalty, always saying "no" is CDT-rational because you expect others to say "no" so should "no" along with them.
If just one has to agree, then you should say "yes" a small percent of the time, because then it's more likely at least one says "yes" in the 18 case than the 2 case
Yes, you are completely correct. Shame on me - I should've thought harder about this case.
Still, my main objection, that Radford Neal is solving a different, more convinient problem, still stands.
I don't understand how you think I've changed the problem. The $50 penalty for not all doing the same thing was an extra "helpful" feature that Eliezer mentioned in a parenthetical comment, under the apparent belief that it makes the problem easier for causal decision theory. I don't take it to be part of the basic problem description. And Eliezer seems to have endorsed getting rid of the anthropic aspect, as I have done.
And if one does have the $50 penalty, there's no problem analysing the problem the way I do. The penalty makes it even more disadvantageous to take the bet when the others are unlikely to take it, as per the prior agreement.
I suspect that you just want to outlaw the whole concept that the different people with green balls might do different things. But in actual reality, different people may do different things.
I don't understand how you think I've changed the problem.
The problem was about dynamic inconsistency in beliefs, while you are talking about a solution to dynamic inconsistency in actions. Your assumption that people act independently from each other, which was not part of the original problem, - it was even explicitly mentioned that people have enough time to discuss the problem and come to a coordinated solution, before the experiment started, - allowed you to ignore this nuance.
Eliezer seems to have endorsed getting rid of the anthropic aspect, as I have done.
As I stated in my post, anthropic and non-anthropic variants are fully isomorphic, so this aspect is indeed irrelevant.
I suspect that you just want to outlaw the whole concept that the different people with green balls might do different things.
The problem is not about what people might do. The problem is about what people should do. What is the correct estimation of expected utility? Based on the P(Heads) being 50% or 90%? Should people just foresee that decision makers will update their probability estimate to 90% and thus agree to take the bet in the first place? What is the probability theory justification for doing/not doing it?
But in actual reality, different people may do different things.
In actual reality all kind of mathematical models happen to be useful. You can make an argument that a specific mathematical model isn't applicable for some real world case or is applicable to less real world cases than a different model. That doesn't mean that you have invalidated the currently less useful model or solved its problems. In general, calling a scenarios, that we can easily implement in code right now, to be "unrealistic thought experiments" and assuming that they will never be relevant, is quite misguided. It would be so, even if your more complicated solution, with different assumptions, indeed were more helpful to the current most common real world cases.
Which isn't actually the case as far as I can tell.
Let's get as close to the real world as possible and, granted, focus on the problem as you've stated it. Suppose we actually did this experiment. What is the optimal strategy?
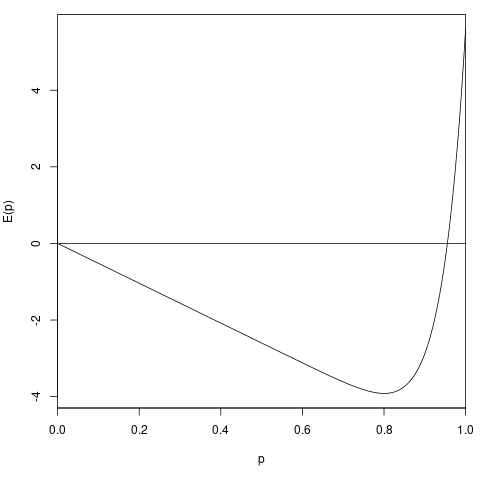
Your graph shows that expected utility tops when p=1. So does it mean that based on your analysis people should always take the bet? No, this can't be right, after all then we are loosing the independence condition. But what about having the probability of taking the bet be very high, like 0.9 or even 0.99? Can a group of twenty people with unsynchronized random number generators - arguably not exactly your most common real world case, but let's grant that too - use this strategy to do better than always refusing the bet?
Your graph shows that expected utility tops when p=1. So does it mean that based on your analysis people should always take the bet?
What this is saying is that if everyone other than you always takes the bet, then you should as well. Which is true; if the other 19 people coordinated to always take the bet, and you get swapped in as the last person and your shirt is green, you should take the bet. Because you're definitely pivotal and there's a 9/10 chance there are 18 greens.
If 19 always take the bet and one never does, the team gets a worse expected utility than if they all always took the bet. Easy to check this.
Another way of thinking about this is that if green people in general take the bet 99% of the time, that's worse than if they take the bet 100% of the time. So on the margin taking the bet more often is better at some point.
Globally, the best strategy is for no one to take the bet. That's what 20 UDTs would coordinate on ahead of time.
I'm having a hard time making sense of what you're arguing here:
The problem was about dynamic inconsistency in beliefs, while you are talking about a solution to dynamic inconsistency in actions.
I don't see any inconsistency in beliefs. Initially, everyone thinks that the probability that the urn with 18 green balls is chosen is 1/2. After someone picks a green ball, they revise this probability to 9/10, which is not an inconsistency, since they have new evidence, so of course they may change their belief. This revision of belief should be totally uncontroversial. If you think a person who picks a green ball shouldn't revise their probability in this way then you are abandoning the whole apparatus of probability theory developed over the last 250 years. The correct probability is 9/10. Really. It is.
I take the whole point of the problem to be about whether people who for good reason initially agreed on some action, conditional on the future event of picking a green ball, will change their mind once that event actually occurs - despite that event having been completely anticipated (as a possibility) when they thought about the problem beforehand. If they do, that would seem like an inconsistency. What is controversial is the decision theory aspect of the problem, not the beliefs.
Your assumption that people act independently from each other, which was not part of the original problem, - it was even explicitly mentioned that people have enough time to discuss the problem and come to a coordinated solution, before the experiment started, - allowed you to ignore this nuance.
As I explain above, the whole point of the problem is whether or not people might change their minds about whether or not to take the bet after seeing that they picked a green ball, despite the prior coordination. If you build into the problem description that they aren't allowed to change their minds, then I don't know what you think you're doing.
My only guess would be that you are focusing not on the belief that the urn with 18 green balls was chosen, but rather on the belief in the proposition "it would be good (in expectation) if everyone with a green ball takes the bet". Initially, it is rational to think that it would not be good for everyone to take the bet. But someone who picks a green ball should give probability 9/10 to the proposition that the urn with 18 balls was chosen, and therefore also to the proposition that everyone taking the bet would result in a gain, not a loss, and one can work out that the expected gain is also positive. So they will also think "if I could, I would force everyone with a green ball to take the bet". Now, the experimental setup is such that they can't force everyone with a green ball to take the bet, so this is of no practical importance. But one might nevertheless think that there is an inconsistency.
But there actually is no inconsistency. Seeing that you picked a green ball is relevant evidence, that rightly changes your belief in whether it would be good for everyone to take the bet. And in this situation, if you found some way to cheat and force everyone to take the bet (and had no moral qualms about doing so), that would in fact be the correct action, producing an expected reward of 5.6, rather than zero.
I don't see any inconsistency in beliefs. Initially, everyone thinks that the probability that the urn with 18 green balls is chosen is 1/2. After someone picks a green ball, they revise this probability to 9/10, which is not an inconsistency, since they have new evidence, so of course they may change their belief. This revision of belief should be totally uncontroversial. If you think a person who picks a green ball shouldn't revise their probability in this way then you are abandoning the whole apparatus of probability theory developed over the last 250 years. The correct probability is 9/10. Really. It is.
I don't like this way of argument by authority and sheer repetition.
That said, I feel totally confused about the matter so I can't say whether I agree or not.
Well, for starters, I'm not sure that Ape in the coat disagrees with my statements above. The disagreement may lie elsewhere, in some idea that it's not the probability of the urn with 18 green balls being chosen that is relevant, but something else that I'm not clear on. If so, it would be helpful if Ape in the coat would confirm agreement with my statement above, so we could progress onwards to the actual disagreement.
If Ape in the coat does disagree with my statement above, then I really do think that that is in the same category as people who think the "Twin Paradox" disproves special relativity, or that quantum mechanics can't possibly be true because it's too weird. And not in the sense of thinking that these well-established physical theories might break down in some extreme situation not yet tested experimentally - the probability calculation above is of a completely mundane sort entirely analogous to numerous practical applications of probability theory. Denying it is like saying that electrical engineers don't understand how resistors work, or that civil engineers are wrong about how to calculate stresses in bridges.
Ape in the coat resolves this by abandoning standard probability theory in favour of a scheme in which a single person can simultaneously hold two different probabilities for the same event, to be used when making different decisions.
I don't think it's a correct description of what I do. If anything, I resolve this by sticking to probability theory as it is, without making any additional assumptions about personhoods.
First of all, it's not the same event. In one case we are talking about event "this person sees green", while in the other - about event "any person sees green". If distinguishing between this two events and accepting that they may have different probabilities doesn't count as "abandoning probability theory", neither is my alternative approach, which is completely isomorphic to it.
Secondly, no theorem or axiom of probability theory claims anything about personhood. People just smuggle in their intuitive idea of it, which may lead to apparently paradoxical results. The only way probability theory can treat personal identities is in terms of possible outcomes. For example in a fair coin toss scenario, "you" is a person who may observe Heads outcome with 1/2 probability and Tails outcomes with 1/2 probability. But so is any other person that observes the same coin toss! If you and me observe the same coin toss, we are the same entity for the sake of the mathematical model. Probability theory doesn't distinguish between physical people, or consciousnesses or metaphysical identities. Only between sets of possible outcomes that can be observed. I'll probably have to elaborate this idea more in a future post.
OK. Perhaps the crucial indication of your view is instead your statement that 'On the level of our regular day to day perception "I" seems to be a simple, indivisible concept. But this intuition isn't applicable to probability theory.'
So rather than the same person having more than one probability for an event, instead "I" am actually more than one person, a different person for each decision I might make?
In actual reality, there is no ambiguity about who "I" am, since in any probability statement you can replace "I" by 'The person known as "Radford Neal", who has brown eyes, was born in..., etc., etc.' All real people have characteristics that uniquely identify them. (At least to themselves; other people may not be sure whether "Homer" was really a single person or not.)
So rather than the same person having more than one probability for an event, instead "I" am actually more than one person, a different person for each decision I might make?
No. Once again. Event is not the same. And also not for every decision. You are just as good as "a different person" for every different set of possible outcomes that you have according to the mathematical model that is been used, because possible outcomes is the only thing that matters for probability theory - not the color of your eyes, date of birth etc.
Maybe it would be clearer if you notice, that there are two different mathematical models in use here: one describing probabilities for a specific person (you), and another describing probabilities for any person that sees green - that you may happen to be or not. The "paradox" happens when people confuse these two models assuming that they have to return the same probabilities, or apply the first model when the second has to be applied.
Quite neat.
But taking the gamble or not depending on your prior (which sort of glosses over some nonzero-sum game theory that should go into getting to any such prior) is still the wrong move. You just shouldn't take the gamble, even if you think other people are.
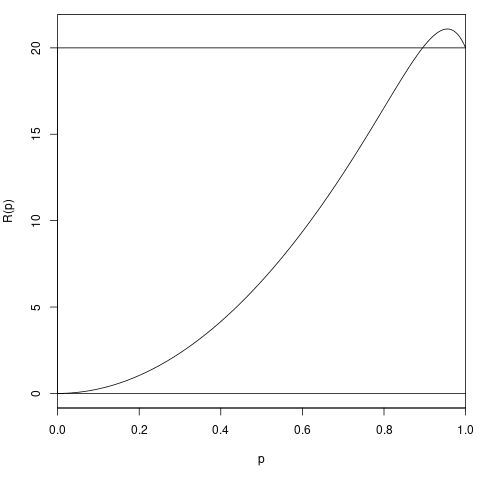
But if for some reason you believe that the other people with green balls will take the bet with probability 0.99, then you should take the bet yourself. The expected reward from doing so is , with E as defined above, which is +3.96. Why do you think this would be wrong?
Of course, you would need some unusually strong evidence to think the other people will take the bet with probability 0.99, but it doesn't seem inconceivable.
I think this is clearer in the non-anthropic version of the game.
- 20 players, and we're all playing for a charity.
- A coin is flipped. Heads, 18 green balls and 2 red balls go in the urn, Tails, 2 green balls and 18 red balls go in the urn.
- Everyone secretly draws a ball and looks at it. Then everyone casts a secret ballot.
- If you have a red ball, your vote doesn't matter, you just have to cast the ballot so that nobody knows how many green balls there are.
- If everyone with a green ball votes Yes on the ballot, then the charity gains $3 for each green ball and loses $1 for each red ball.
In this game, if you draw a green ball, don't vote Yes! Even if you think everyone else will.
This might be surprising - if I draw a green ball, that's good evidence that there are more green balls. Since everyone voting Yes is good in the branch of the game where there are 18 green balls, it seems like we should try to coordinate on voting Yes.
But think about it from the perspective of the charity. The charity just sees people play this game and money comes in or goes out. If the players coordinate to vote Yes, the charity will find that it's actually losing money every time the game gets played.
I think you're just making a mistake here. Consider the situation where you are virtually certain that everyone else will vote "yes" (for some reason we needn't consider - it's a possible situation). What should you do?
You can distinguish four possibilities for what happens:
- Heads, and you are one of the 18 people who draw a green ball. Probability is(1/2)(18/20)=9/20.
- Heads, and you are one of the 2 people who draw a red ball. Probability is (1/2)(2/20)=1/20.
- Tails, and you are one of the 2 people who draw a green ball. Probability is (1/2)(2/20)=1/20.
- Tails, and you are one of the 18 people who draw a red ball. Probability is (1/2)(18/20)=9/20.
If you always vote "no", the expected reward will be 0(9/20)+12(1/20)+0(1/20)+(-52)(9/20)=-22.8. If you always vote "yes", the expected reward will be 12(9/20)+12(1/20)+(-52)(1/20)+(-52)(9/20)=-20, which isn't as bad as the -22.8 when you vote "no". So you should vote "yes".
Sorry, right after posting I edited my reply to explain the reasoning a bit more. If you're purely selfish, then I agree with your reasoning, but suppose you're "playing for charity" - then what does the charity see as people play the game?
The charity sees just what I say above - an average loss of 22.8 if you vote "no", and an average loss of only 20 if you vote "yes".
An intuition for this is to recognize that you don't always get to vote "no" and have it count - sometimes, you get a red ball. So never taking the bet, for zero loss, is not an option available to you. When you vote "no", your action counts only when you have a green ball, which is nine times more likely when your "no" vote does damage than when it does good.
Ah, thanks for being patient. Yes, you're right. Once you've fixed beliefs about what everyone will do, then if everyone votes yes you should too. Any supposed non zero sum game theory about what to do can only matter when the beliefs about what everyone will do aren't fixed.
Late to the party but want to say this post is quite on point with the analysis. Just want to add my—as a supporter of CDT—reading to the problem, which has a different focus.
I agree the assumption that every person would make the same decision as I do is deeply problematic. It may seem intuitive if the others are "copies of me", which is perhaps why this problem is first brought up in an anthropic context. CDT inherently treats the decision maker as an agent apart from his surrounding world, outside of the casual analysis scope. Assuming "other copies of me" giving the same decision as I do put the entire analysis into a self-referential paradox.
In contrast the analysis of this post is the way to go. I shall just regard the others as part of the environment, their "decision" are nothing special but parameters I shall considered as input to the only decision-making in question—my decision making. It cuts off the feed back loop.
While CDT treating the decision maker as separate-from-the-world agent outside the analysis scope is often regarded as it's Achille's heel, I think that is precisely why it is correct. For decision is inherently a first-person concept, where the free-will resides. If we cannot imagine reasoning from a certain thing's perspective, then whatever that thing outputs are mere mechanical products. The concept of decision never applies.
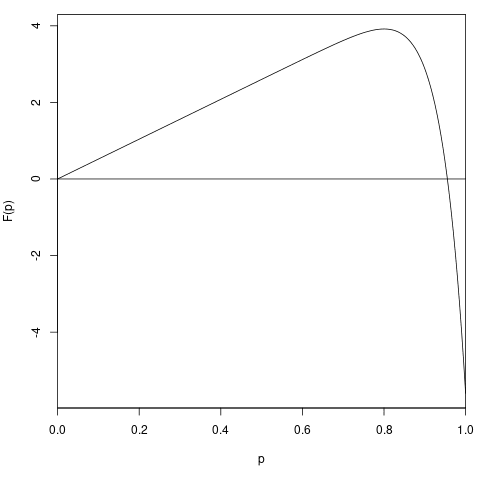
I diverge from this post in the sense that instead of ascribing this reflective inconsistency paradox to the above mentioned assumption, I think its cause is something deeper. In particular, for the F(p) graph, it shows that IF all others sticks to the plan of p=0.9355 then there is no difference for me to take or reject the bet (so there is no incentive to deviate from the pregame plan.) However, how solid is it to assume that they will stick to the plan? It cannot be said that's the only rational scenario. And according to the graph if I think they deviated from the plan then there so must I. Notice in this analysis there is no forcing others' decisions so they must be same as mine, and our strategies could well be different. So the notion that the reflective inconsistency resolves itself by rejecting the assumption of everyone makes the same decision only works in the limited case if we take an alternative assumption that the others all stick to the pregame plan (or all others reject the bet.) Even in that limited case, my pregame strategy was to take the bet with p=0.9355 while the in game strategy was anything goes (as they do not make a difference to the reward). Sure there is no incentive to deviate from the pregame plan but I am hesitant to call it a perfect resolution of the problem.
Curated and popular this week