Initial observations and results (warning, for all I know right now it could be substantially complete solution):
It looks like the non-Carver bidders for newer carcasses are consistent, and drop linearly with age in days:
snow serpents: 60 - 20*age
winter wolf: 50-12*age (technically we don't have a third point to see that this is linear, but see below)
yeti: 55-6*age
Presumably, this is due to a single bidder. The trend continues until it drops below the distribution for older carcasses, so I guess that this bidder continues to bid this pattern down to 0 sp.
For older carcasses, there is a range of variation that doesn't seem to depend much on age. I therefore assume for now that it really doesn't depend on age, though for all I know it does.
For winter wolf, Carver won all the auctions for 2 and 3 day carcasses. However, Carver bid high enough for this data to be consistent with 2 day old winter wolves following the linear trend and 3 day old winter wolves following the old-carcass distribution, so I am assuming that they do follow these trends.
One potential pitfall in assessing this distribution for older carcasses is that where Carver also bids within the range, the lower non-Carver bids are more likely to be overbid by Carver. Ignoring this for now. For 4 day old yetis, the new-Carver bidder would fall within the expected older-carcass non-Carver bid distribution, though all actual bids were higher. Ignoring this as well.
The old-carcass distribution appears to be:
snow serpent: 10-17, but heavily skewed to higher values
winter wolf: 20-23, possibly some skew to higher values
yeti: uniformish 30-35, though with few data points, could also have some skew to higher.
In terms of revenue obtained, Yetis and Winter Wolves appear to show a linearish decline with age, while Snow Serpents appear roughly constant. Assuming such linearity/constantness:
snow serpent expected revenue: 27.15
winter wolf expected revenue: about 39 -2*age
yeti expected revenue: about 75-3.4*age
Solution based on the above:
Lot 1, Yeti, 0 days: bid 56 to beat expected new-carcass bid of 55. Expected profit about 19sp, we have 344 sp remaining.
Lot 2, Snow Serpent, 2 days: bid 21 to beat expected new-carcass bid of 20, 7 sp expected profit. 323 sp remaining.
Lot 3, Snow Serpent, 1 day: no profitable bid expected, skip.
Lot 4, Winter Wolf, 1 day: no profitable bid expected, skip.
Lot 5, Yeti, 5 days: bid 36 as there is enough likelihood of a bid up to 35 to avoid losing the ~22sp expected profit. 287 sp remaining.
Lot 6, Winter Wolf, 1 day: skip as with previous 1 day winter wolf
Lot 7, Snow Serpent, 1 day: skip as with previous 1 day snow serpent
Lot 8, Snow Serpent, 5 days: bid 18 as there is enough likelihood of a bid of 17 to make it not worth risking losing the ~9sp expected profit. 269 sp remaining.
Lot 9, Winter Wolf, 3 days: bid 24 as there is enough likelihood of a bid of 23 to make it not worth risking the ~9sp expected profit. 245 sp remaining.
Lot 10, Winter Wolf, 7 days: at an expected revenue of ~25, it is worth going down to 23sp to get ~2sp profit though we might lose. Going down to 22sp looks like it will reduce the chances of getting it by more than a third for less than 50% gain, not worth it. So, bid 23sp, ~2sp profit, 222 sp remaining.
Lot 11, Winter Wolf, 8 days: at an expected revenue of a bit over 23, it is worth going down to 22sp, but not to 21sp (which halves or slightly more than halves success chance for less than a doubling of revenue. So, bid 22sp, ~1sp profit, 200 sp remaining.
Lot 12, Snow Serpent, 8 days: bid 18 for same reason as any other old snow serpent. ~9sp profit, 192 sp remaining.
Lot 13, Winter Wolf, 2 days: bid 27 to beat expected new-carcass bid of 26 (even though we have no 2-day winter wolf non-Carver bids to confirm this); expected profit ~8sp, 165 sp remaining.
Since we have lots of sp remaining, I go back and put in bids for the 1 day winter wolves and snow serpents I skipped. Specifically, I'll put in 18 for the one day snow serpents and 24 for the one day winter wolves to beat the old-carcass bid distribution in case the new-carcass bidder doesn't show up.
A potential model of the full problem (involves questionable numerology):
There are 13 lots currently, and the number of carcasses in the record is divisible by 13 (129*13). If we include the current auctions, that's 13*130, or 13*13*10.
So, I'll assume that all auctions have 13 lots.
The individual monster types aren't divisible by 13 (except Snow Serpents), nor are they if we include the current auctions (except Winter Wolves). However, the Wolf:Yeti ratio seems very close to 3, and if the overall ratios were 2:5:6 that would fit in with the 13 theme and seems close enough to the Yeti:Serpent:Wolf ratio.
The age distributions look fairly triangularish, with a maximum age of 11. One possible way to express that would be there is on average 1 carcass of age 11 for every 2 aged 10, up to every 12 aged 0. And what's 1+2+...12? Of course - a multiple of 13. Specifically 13*6.
Now, it would be nice if looking at the data in blocks of 13*6 showed some pattern, but I don't see one, nor is the data a multiple of 6. No matter, we will press on without such empirical validation.
I also note that, in the current auction, the early lots look newer than the late auctions. Coincidence? Probably.
So, model:
Base Lot Generation (low confidence):
Auction of 13 lots each day
Each lot assigned an age from 0 to 11 by a random distribution weighted by {12-age}
Each lot assigned an animal type by a random distribution weighted 2:5:6 for Yeti:Serpent:Wolf
Bids: There are two non-Carver bidders, one of whom bids:
60-20*age for Snow Serpents
50-12*age for Winter Wolves
55-6*age for Yeti
and the other one bids:
9+d8 for Snow Serpents
19+d4 for Winter Wolves
29+d6 for Yeti
whereas Carver bids (not high confidence):
7+2d10 for Snow Serpents
31+2d8-3*age for Winter Wolves
32+2d20-2*age for Yeti
Revenue: (credit to GuySrinivasan)
20+2d6 for Snow Serpents
25+4d6-2*age for Winter Wolves
72+1d6-{age}d6 for Yeti (assuming that the prior for d6's over d5's is stronger than the 45 times better fit for a d5 in the base part of this formula)
Love it!
The age distribution is very clearly off, though. Age 0 has about 2.5x the count of age 1, for each species. I didn't see anything come up clearly...
The age 0 amount is higher than expected from the model distribution, but it's nowhere near 2.5x the age 1 amount. I have:
Overall 289 age 0, 233 age 1 (expected 258, 236.5)
Snow Serpents 103 age 0, 92 age 1
Winter Wolves 141 age 0, 108 age 1
Yeti 45 age 0, 33 age 1
Thank you, my bin size was bad. :(
Still gonna guess that somehow this is from a distribution more easily generated than the triangular. But I may be overfitting on the last time I said something was triangular and it turned out to be exponential. Still, it looks to me like "start at age=0; roll a d6; if you rolled 1-5, add 1 to age and repeat, otherwise on 6 stop; if you reach age 12, discard and start again from age=0" is a decent match for this distribution, and it involves a d6, so that's my guess I think.
Looks like the likelihood for triangular is over a million times better (to log-nearest order of magnitude ~10^-1672 v. ~10^-1679) than the 1/6 drop per turn exponential.
Anyway, in the spirit of tumbling platonic solids:
One possible distribution for the age numbers would be the distribution generated by min(d12,d12)-1. This is not the same as the 1,2,3,4...12 triangular distribution, but rather a 1,3,5,7,...23 triangular distribution. (The 1,2,3...12 distribution would be generated by min (d12, d13)-1).
And checking the likelihood - this one is actually better.
LOG10 likelihood
-1672.05 for 1,2,3,...12
-1671.43 for 1,3,5,...23
P.S. I was terse in the previous comment because of time constraints. About the difficulty of the triangular distribution, I was thinking it wasn't that unlikely anyway because in the previous problem abstractapplic generated a weighted average by taking a random entry from a list that contained duplicates, and a suitable list could be generated easily enough using a for loop.
To save anyone time if they want to read my decision, it's the same as GuySrinivasan's better formatted decision except on lots 10 and 11, where I took seriously the statement that we're indifferent to work and bid 1 sp higher than GuySrinivasan did.
Above I explicitly noticed that Carver's bids would distort the distribution, set that aside, then, when I encountered a skewed distribution, failed to think to attribute it to Carver's bids. But of course that would be the obvious explanation.
I looked at this, and found that the actual distribution does match pretty well what I'd expect if the true distribution of non-Carver bids were a uniform distribution for old carcasses, though the skew effect was only really dramatic for Snow Serpents anyway.
(edit): Assuming this is correct, we can now better calculate the probability of losing if we bid lower.
For Lot 10: 23 v. 22 sp on 7 day wolf, we cut win rate by exactly 1/3 going down to 22, the revenue is a bit over 25 by my linear fit or exactly 25 by GuySrinivasan's formula; meaning, if GuySrinivasan is right then the average profit is exactly the same either way.
For Lot 11: 22 v. 21 sp on 8 day wolf, we exactly halve win rate going down to 21, the revenue is a bit over 23 by my linear fit or exactly 23 by GuySrinivasan's formula; meaning, if GuySrinivasan is right then the average profit is exactly the same either way.
(edit2): A further note - Even though accounting for Carver's bids when calculating the old-carcass bid distribution dramatically reduces the loss probability from bidding low on Snow Serpents, it's still not worth it to bid low on them (since 1/8 probability of losing more than makes up for profit going from 9 to 10). However, if the parameters of the problem had been changed a bit, this could have been a nice trap.
(edit3): Or wait - do we actually know that the non-Carver bid distribution for Snow Serpents only goes down to 10? what if it goes down to 8 or lower, but we miss those because carver bids over those? Carver's bids go down to 9, so we could theoretically see a 9 non-Carver bid, but the data might not include any by coincidence. We can't possibly see a non-Carver bid below 9. Looking at this - no, if it goes down to 8, the number of non-Carver bids we'd expect to see seems too low - I'm reasonably confident it doesn't go down that low.
Mostly not tricky; a few little tricky bits with 1-silver quibbles for expected profits of just half a silver difference. Somehow we don't care about butchering more for tiiiiny profits, otherwise I'd just skip 'em and forgo a latte to gain back some time to... hm, maybe all this winter stuff means butchering is the most fun thing I could be doing. Nah, I can think of at least something more fun. If I see two possible bids off by small fractions of a silver in expectation, I'm placing the lower bid and getting my theoretically non-existent non-butchering-time equity.
| lot | bid |
|---|---|
|1|56|
|2|21|
|3|18|
|4|24|
|5|36|
|6|24|
|7|18|
|8|18|
|9|24|
|10|22|
|11|21|
|12|18|
|13|27|
This is well within budget, at 327sp, so we don't need to worry about saving silver for lucrative late lots. And we expect to lose some of these bids anyway.
Revenue from selling butchered parts is, I think,
Snow Serpent: 20+2d6
Winter Wolf: 25+4d6 - 2*age
Yeti: 70+1d6 - {age}d6
EDIT: prodded and helped by simon, Yeti is revised to 72+1d6-{age}d6 for me. This is 45x less likely than 72+1d5-{age}d6 by the likelihood, but I'm deciding to say the universe-simplicity-priors against using a d5 there outweigh the 45x.
Your yeti revenue distribution would predict a maximum of 76 at day 0, but we see 77. We also don't see anything below 73. I suggest 72 + 1d5 at day 0.
The full formula would be then 72 + 1d5 - {age}d6, where these are independent d6 rolls, and not a single roll multiplied by the age (I think this is what you meant, but clarifying since I wasn't 100% sure on the terminology used). (The other interpretation would lead to too high variation at high ages, I think).
The formulas for Snow Serpent and Winter Wolf look consistent with the data to me.
Yeah I debated that, and some other similar modifications, but in the end my priors on what the natural laws of these worlds look like overrode what looks like it might be a better fit. We shall see...
And yes, I was using standard https://en.wikipedia.org/wiki/Dice_notation
OK, I see such an argument for the die used, but the base value proposed can't be correct with that die.
:facepalm: that's what I get for switching at the last minute. You're absolutely right, of course.
I originally had 78 - {age+1}d6 but I figured there was no way that was actually the original formula. I don't particularly like 71 + 1d6 - {age}d6 either. The means make "-{age}d6" look really good, but I don't see any "nice" way to start it off. 72+1d5, like you said, looks great distribution-wise but 72 < {20,25} and 1d5 < {all the d6s}. 71+1d6 takes a hit on never rolling a 1 but gets a boost from 1d6 vs 1d5.
OK I calculated the likelihoods of getting the full yeti revenue data set for those distributions and got the following results:
For 78-{age+1}d6 (which is equivalent to 71+1d6-{age}d6):
likelihood ~ 10^-192
For 72 + 1d5 - {age}d6:
likelihood ~10^-189
So the 1d5 version is literally 1000 times better fit to the data, and I doubt that the prior for 1d6 over 1d5 is that strong. Besides, the base value of 72 is a round number in a way, might increase the 1d5 prior a bit. I'd definitely bet on the 1d5 version over the 1d6.
That's pretty convincing. Let's try all the maybe-reasonable-ish versions:
71+1d6-{age}d6 has log[10] likelihood of -192.02
72+1d6-{age}d6 has log[10] likelihood of -190.57
72+1d5-{age}d6 has log[10] likelihood of -188.91
71+1d6-{age}d5 has log[10] likelihood of -196.42
72+1d6-{age}d5 has log[10] likelihood of -206.39
72+1d5-{age}d5 has log[10] likelihood of -200.41
Definitively -{age}d6, sure. Now here's a much tighter question: what about
72+1d6-{age}d6?
It takes a x45 hit on the likelihood compared to
72+1d5-{age}d6, which is pretty big, but I think I'm willing to say the chances of using a lone 1d5 right there are a bigger penalty. So my revised guess is 72+1d6-{age}d6.
Nice analysis! But I am not so confident on how strong the prior should be and am somewhat torn on the conclusion.
I've started looking at the data and have a model, but the implementation of the model isn't finished (doubt I'll do it anytime soon). You can find my thoughts in this Colab with some nice looking figures ;).
Main findings are:
- Days 0, 1 and 2, others bid entirely deterministically.
- Days >= 3, bidders bid with what seem to be the same distribution.
- Revenue for Winter Wolf follow about the same distribution but with linearly decreasing mean.
- Revenue for Yeti seem to have linearly decreasing mean and linearly increasing standard deviation.
- Revenue for Snow Serpent don't seem to change with time.
Nice graphs in the colab.
For the bidder model, the Yeti day=3 data is consistent with the Days 0,1,2 line and not with the days >=4 distribution, and in general, whichever of the new-carcass line or old-carcass distribution would be higher is what we see.
So, my model would be that there are two other bidders, one who makes deterministic linear bids and one who bids in a uniform distribution (see my reply to my top-level comment); both bid on everything (well, I guess as long as the bid is >0), but we don't see the lower bid.
Yes, in retrospect I agree with you. That is a more reasonable model than I got from squinting at the plots.
My fairly low-effort attempt:
My goal here was roughly to minimize the amount of manual analysis. I used Python to graph the mean revenue by species and age, and also estimate the distribution along which other bidders bid.
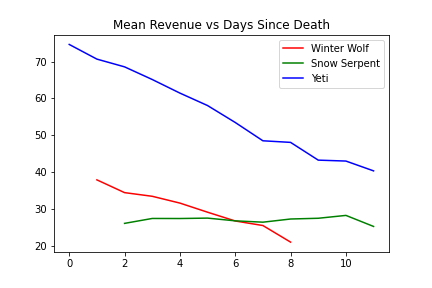
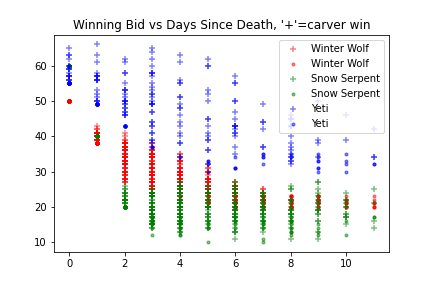
Everything seems roughly linear, with perhaps some nonlinearity in winter wolf bids. Given that the sample mean revenue should be an unbiased estimator of revenue, and the probability of winning for a given bid should also be an unbiased estimator, we can use linear regression for each species to estimate revenue, and logistic regression on (age, bid) to estimate the probability of winning a given auction with a given bid.
Using logistic regression implicitly assumes the distribution is logistic, which might be problematic but seems okay. Since we want to maximize expected profit = p_win(bid) * (revenue - bid), we can throw this into the scipy black-box optimizer to find the bid price that maximizes profit. This gave us the following bids:
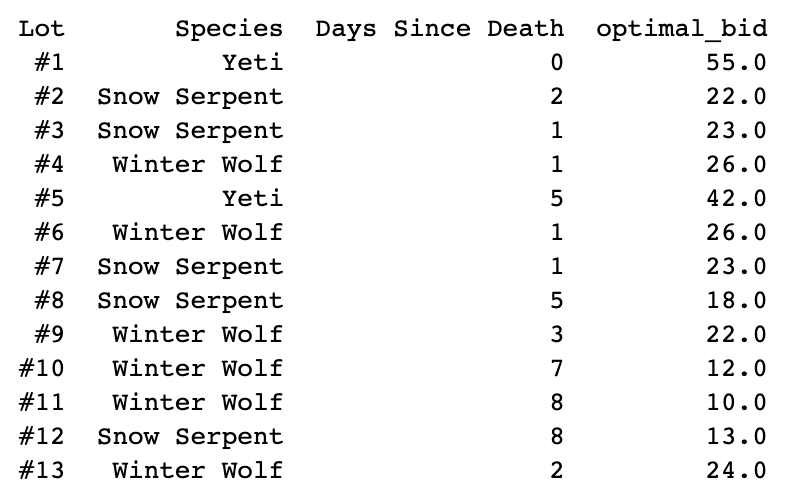
One could probably do better by actually looking at the distribution of non-carver winning bids, but I don't know the best way to account for selection (using the distribution directly would create a biased distribution, since they're always higher than the carver bid).
I didn't get around to this until 5/15, so the answers had been revealed, but I didn't peek. I made a simple spread sheet so I could look at all the cases by species and age.
My bids were
1: 60, 2: 21, 3:25, 4:30, 5:47, 6:30, 7:25, 8: 18, 9:24, 10:22, 11:20, 12:19, 13: 27
MY results were:
You net a profit of 71sp
(The Expected Value of your strategy was 68sp)
Spoiler protection.
Long term pattern of prices falling with time since killed for all monsters.
Yeti are consistently the cheapest. Winter Wolfs start of as the most expensive, but as time since killed
increases the Snow Serpent becomes roughly equal.
Yeti have yielded the highest profit with Snow Wolf the highest losses.
From the description it looks like the winning bid and profit should be independent.
For each lot find similar lots in the past. From the ones Carver didn't win we can estimate the probability of winning for each possible bid, and from the ones she did win we can estimate the amount of money to be made by selling it. For each lot we can then look for the bif which maximises P(Winning)*Estimated profit.
Yeti 0 days since killed. All other winning bids at 55. 56 Should win with an estimated 18 profit.
Snow Serpent 2 days since killed. All other bids were at 20. 21 should win with estimated 5 profit.
Snow Serpent 1 day since killed. All other bids were at 40. 41 should win with UNKNOWN profit.
Winter Wolf 1 day since killed. All other bids were at 38. 39 should win with estimated -2 profit.
Yeti 5 days since killed. Other bids between 30-33. 34 should win with estimated 24 profit, but there are only 4 other winners, so the risk of losing unless we bid more seem realistic, but that probably won't offset the risk of losing if we win.
Winter Wolf 1 day since killed. All other bids were at 38. 29 should win with estimated -2 profit.
Snow Serpent 1 day since killed. All other bids were at 40. 41 should win with unknown profit.
Snow serpent 5 days since killed. Other bids 10-16. 17 should win with estimated 10 profit, but only 6 cases where other bidders won. Winter wolf 3 days since killed. Carver won all of these by bidding between 24 and 38 average selling price was 33.
Winter Wolf 7 days since killed. Other bids between 20 - 23. Bidding 24 generates an estimated 1 profit.
Winter Wolf 8 days since killed. Other bids at 20-23. 24 Wins at estimated -3 profit.
Snow Serpent 8 days since killed. Other bids between 12 and 17. 18 wins with an estimated profit of 9.
Winter Wolf 2 days since killed. No non Carver winners. Craver bid between 27 and 41 with an average selling price of 34.
For the cases where there are no non Carver winners it seems reasonable to enter the lowest bid. There are a number of cases where the best non Carver bid is constant, so there is a realistic chance that dropping the bid will guarantee that we don't win. Whilst there are only a few at the lowest bid it looks like increasing the bid will reduce the expected profits more than can be expected to be gained by increasing the odds of winning.
For the cases where the profit is unknown. Looking at the other data the selling price only seems to drop
by a few sp per day. This suggests that we probably can't make a profit on the Snow Serpent unless we submit a low bid and get very lucky. Guess and knock a modertae value (10sp) off the average bid
Where the expect profit is < 0 put in a cheeky low bid just on the off chance we can pick one up cheap.
Do this at one below the lowest selling price where there are a reasonable number, otherwise guess and knock 10sp off.
So we have:
lot 1 Yeti 0 days since killed - 56sp
lot 2 Snow Serpent 2 days since killed - 21 sp
lot 3 Snow Serpent 1 day since killed - 30sp
lot 4 Winter Wolf 1 day since killed - 29sp
lot 5 Yeti 5 days since killed - 34sp
lot 6 Winter Wolf 1 day since killed - 29sp
lot 7 Snow Serpent 1 day since killed - 30sp
lot 8 Snow Seppent 5 days since killed - 17sp
lot 9 Winter Wolf 3 days since killed - 24sp
lot 10 Winter Wolf 7 days since killed - 24sp
lot 11 Winter Wolf 8 days since killed - 11sp
lot 12 Snow Serpent 8 days since killed - 18sp
lot 13 Winter Wolf 2 days since killed - 27sp
350sp in total so we don't have to worry about losing later lots because we spent too much earlier.
Snow Serpent bid price is always 60/40/20 for 0/1/2 day old lots, never above 17 for older. Sale value is independent of age averaging around 27.2
Winter Wolf bid price is always 50/38 for 0/1 day old lots, never above 23 for older. Sale value ranges from 37.9 for 1d lots to 25.5 for 7d lots. Older than 7d probably not worth bidding on.
Yeti bid price is always 55/49/43/37 for 0/1/2/3 day old lots, never above 35 for older. Sale value ranges from 74.6 for 0d lots to around 42 for 9-11d lots.
Based on the anticipated bid price and expected sale value of each lot, I calculated a profit margin for each as (sale - win)/win.
Lot # Bid Win Sale Profit Margin
5 35 36 58.1 22.1 61.4%
8 17 18 27.2 9.2 51.1%
12 17 18 27.2 9.2 51.1%
13 23 24 34.4 10.4 43.3%
9 23 24 33.4 9.4 39.2%
1 55 56 74.6 18.6 33.2%
2 20 21 27.2 6.2 29.5%
10 23 24 25.5 1.5 6.3%
4 38 39 37.9 -1.1 -2.8%
6 38 39 37.9 -1.1 -2.8%
11 23 24 23.0 -1.0 -4.2%
3 40 41 27.2 -13.8 -33.7%
7 40 41 27.2 -13.8 -33.7%
I had planned to use a greedy algorithm to pick the most profitable lots until I ran out of money, but actually I can afford to be competitive on all marginally profitable lots. My final bids are as follows. (* indicates I do not expect to win this lot.) I expect to spend 221sp on 8 lots and earn about 308sp from their sale.
Lot #1: 56sp
Lot #2: 21sp
Lot #3: 27sp*
Lot #4: 24sp*
Lot #5: 36sp
Lot #6: 24sp*
Lot #7: 27sp*
Lot #8: 18sp
Lot #9: 24sp
Lot #10: 24sp
Lot #11: 20sp*
Lot #12: 18sp
Lot #13: 24sp
You are an apprentice to Carver, the most successful butcher in your tiny, snow-swept village. Today, for the first time since you joined her, she is sending you to buy carcasses at the daily Auction.
(The (first-price, sealed-bid) Monster Carcass Auction began as a collective effort by local shopkeepers to divert Adventurers from trying to sell them random corpses, but has since become an integral part of the village economy, as well as the population’s main protein source.)
Carver thinks you should trust your instincts and bid however feels right. It’s an approach that’s served her well thus far – the record you’ve been compiling of her bids and subsequent sales attests to that, among other things – but you suspect a more data-driven approach would work better. And if you do well enough on this expedition, that might suffice to prove it to her.
You make sure to arrive at the very end of the event, like your boss always does; this means you’ll lose any tie-breakers – matching bids are resolved in favour of whoever bid first – but also means your rivals will have already put in their bids, so none of them will be able to change their bidding strategy to account for Carver’s absence.
The lots available are as follows:
(As usual, this is all the information given to bidders; the original organizers took the term ‘blind auction’ a little too literally, and by the time anyone realized, the practice of hiding almost everything about the lots had become a tradition.)
You and your employer are risk-neutral, and don’t care how much or little time and effort you spend butchering. You brought 400 silver pieces. How much will you bid for each lot?
Notes:
I’ll be posting an interactive letting you test your decision, along with an explanation of how I generated the dataset, sometime next Friday. I’m giving you a week, but the task shouldn’t take more than a few hours; use Excel, R, Python, Ouija boards, or whatever other tools you think are appropriate. Let me know in the comments if you have any questions about the scenario.
If you want to investigate collaboratively and/or call your decisions in advance, feel free to do so in the comments; however, please use spoiler tags or rot13 when sharing inferences/strategies/decisions, so people intending to fly solo can look for clarifications without being spoiled.