I just spent five minutes on a fun little math problem lurking in your post. The Nash solution uses a family of hyperbolas, so it's natural to ask the question: what other curves could be used instead? In other words, which families of curves are invariant under scalings in x and y? Turns out it's easy to prove (try it!) that all such families have the form x^a*y^b=c, where a and b are constant but c varies. These are the "generalized Nash solutions" where the players have unequal "bargaining powers". For further reading see this PDF.
In your Romantic Dinner / Battlestar Galactica example, it's not really clear what it means for one person to translate or scale their utility function. I'm going to take a newbie stab at it here, and please correct me if this is wrong:
Scaling: This is where the outcome matters more to one party than to the other party. For an extreme example, one person stands to gain between 0 and 10 minutes of extra life from the bargain, and the other person could gain between 0 and 500 years of extra life. And these are totally selfish people, who genuinely don't care about each other's utility; they just want to reach a bargain that optimizes their own utility. The total-utility-maximizing answer would favor the person who has the most to gain, and either person could turn this to their advantage by claiming to really, really care about the outcome. "I'll literally die if we don't watch Battlestar Galactica!", or some such thing.
Translation: This just adds or subtracts a constant amount of utility to any person's utility function. "I would love to watch BSG, but I'm so happy just being with you! ♥". If one person will be disgruntled if they don't (e.g.) have a romantic dinner, and the other person will be at least fairly cheerful either way, then this could influence the bargaining -- and if so, it gives a selfish person a way to game the system, by acting unhappy when they don't get their way.
The way to take advantage of people using the naive egalitarian or utility-sum-maximizing decision methods is to exaggerate how much you care about things, and sulk when you don't get your way. Also known as "acting like a toddler", which our society frowns on, probably for exactly this reason.
Is this reasonably accurate?
I just want to express my disagreement with the other two replies to this comment. Yes, in a vacuum, it's true that scaling and translating utility functions doesn't have any effect. But as soon as you start trying to compare them across individuals -- which is exactly what we were doing in the relevant part of the post -- it seems to me that scaling and translation behave just like this comment describes.
It doesn't mean anything to translate or scale a utility function. A utility function is just a mathematical way to encode certain relative relationships between outcomes, and it turns out if you add 42 to every value of the function, it still encodes those relationships faithfully. Or if you multiply everything by 9000.
This is why comparing two individuals' utility functions in any naive way makes no sense: their functions are encoding relative preference relationships, but it doesn't matter if one of them multiplies everything by 9000. So any comparison that breaks when one of them multiplies everything by 9000 or adds 42 to everything but the other doesn't isn't actually making correct use of the underlying relative preference relationships.
The scaling and translations don't correpsond to anything real. It's simply that if I have a utility function that has value u1 in world w1 and u2 in world w2, and u1 > u2, then I prefer w1 to w2. However, if I add a constant c to my utility function, then the utility of world w1 becomes u1 + c and that of w2 become u2 + c: I still prefer world w1 to w2!
Similalrly, if you generalise to all worlds, then adding c doesn't change my utility at all: I will always have the same preferences as I did before. An agent with the same utility function, plus a constant, will alwaus make the same decisions whatever the value of that constant. The same goes for multiplication by a (positive) scalar. Since these "affine transformations" don't change your preferences, any reasonable system of bargaining should be indifferent to them.
The mathematical object in question is a pair of utility functions. We have to chose how we lift the concept of an affine transformation of a utility function to an affine transformation of a pair of utility functions.
One choice is to define an affine transformation of a pair of utility functions (u,v) as pair of affine transformations (f,g) which take (u,v) to (fu, gv). With this choice we cannot compare the component utility functions within a pair.
Another choice is to define an affine transformation of a pair of utility functions (u,v) by applying a single transformation f to both components getting (fu, fv). This preserves comparisons within the pair.
The key point is that our inability to do interpersonal comparisons of utility is a modeling assumption. It is something we put in to the analysis, not something that we get out of the analysis.
sketerpot is asking "why can't we just compare the utilities?" and in the same comment noticing that there are problems with discovering utilities. What is to stop people exaggerating their utilities in order to game the bargaining system?
sketerpot's comment pretty much nails the situation. Since permitting interpersonal comparisons of utility opens a huge can of worms an important leg of the broader project is to say: Let us assume that interpersonal comparison of utility is impossible, and press on with the analysis to find what solutions to the bargaining problem are available under this assumption.
Utility scaling/translation can mean something if you're scaling them to normalize the average and standard deviation (or other spreading statistic) of reported marginal utilities in group decisions over time; see my comment above.
ETA: In case it's not clear, I agree that a choice of scale for your utility function doesn't mean anything by default, and you're right to be pointing that out, because people mistaken assume that way too often. But if you scale it with a certain purpose in mind, like group decision making, utility can take on additional meaning.
An example of what I mean: if you and I have to make a series of binary decisions as a two-person team, we could each report, on each decision, what is the marginal utility of option 1 over option 2, using a scale of our own choosing. Reporting marginal utility eliminates the choice of translational constant, but we are still scaling our answers according to some arbitrary choice of unit. However, suppose we expect to make, say, 100 decisions per year. We can make a rule: the absolute values of the marginal utilities you report must add up to less than 1000. In other words, you should choose your units so the average absolute marginal utility you report is around 10, or slightly less. This will result in a certain balance in our decision-making procedure: you can't claim to care more than me on every decision; we will end up having about the same amount of influence on the outcomes.
But again, this doesn't mean numerical utilities are intrinsically comparable across individuals. The comparison depends on a choice of scale,.a choice that can be tailored to differing purposes and hence give different meanings to the numerical utilities.
You got it: sharing decision utility is sharing power, not welfare..
A way to prevent people exaggerating how much they care about stuff is to mandate that, on average, people should care the same amount about everything. This is, very approximately, what I do with my close friends to make our mutual decisions quicker: so we don't accidentally make large sacrifices for small benefits to the other, we say on a scale from 1-5 how much we care about each decision, and the larger carer decides.
Example: "Where do you want to go for dinner? I only care 2." "I care 3 (because I have a bad stomach). Let me decide."
Over time, we've gotten faster, and just say the numbers unless an explanation is necessary. It's a nice system :) I'd hate to think my friend would make large sacrifices to benefit me only small gains, and conversely, so that's what we do.
It's worth mentioning that (FWICT) these things are called bargaining problems in the literature: https://en.wikipedia.org/wiki/Bargaining_problem
Why does your disagreement point lie outside the set of possible outcomes? If both are derived from the same game, one should lie within the other.
Otherwise, great post and great diagrams. Thanks. Will your next post give a proof of your conjecture from Mar 15?
Why does your disagreement point lie outside the set of possible outcomes? If both are derived from the same game, one should lie within the other.
To emphasis it's essential arbitrariness :-)
Otherwise, great post and great diagrams. Thanks. Will your next post give a proof of your conjecture from Mar 15?
Thanks! I don't know my conjecture form Mar 15, but the result I have is a new one. Essentially it deals with how to maximise utility when you're unsure about what games you'll be playing. I'm still checking it, and ageing it.
Very nice. I had been thinking about doing this too, but you beat me to it.
In a subsequent post, I'll critique these bargaining solutions, and propose a more utility-maximising way of looking at the whole process.
I'm guessing you are referring to Nash's program here, and the Rubinstein bargaining process. Great. But if you are going to suggest an alternative to NBS and KSBS that is more "utilitarian" in spirit - well that would be interesting too.
But if you are going to suggest an alternative to NBS and KSBS that is more "utilitarian" in spirit - well that would be interesting too.
That's what I'm suggesting; essentially it deals with how to maximise utility when you're unsure about what games you'll be playing. I'm still checking it, and ageing it.
I don't think so; for instance, I don't think Harsanyi's solution is pareto-optimal - though I might be wrong about this, I'm not yet fully following it.
Well, if you think you can bargain to a Pareto-optimal solution, in a game with imperfect information, then I want to see that idea. Because with neither player having enough information to even recognize Pareto-optimality, I don't see how their bargaining can bring them there.
Though perhaps you have a definition of Pareto-optimality in mind in which the optimality is "in the eye of the beholder". Something like that might make sense. After all, in the course of bargaining, each party gains information about the state of the world, which may result in changes in their expected utility even without a change in objectively expected outcome.
Pareto-optimal in expected utility; and yes, "in the eye of the beholder". The μSMBS I described http://lesswrong.com/lw/2xb/if_you_dont_know_the_name_of_the_game_just_tell/ are Pareto optimal (in the eyes of both players), even if they have different probability distributions over the games to be played (I put that in initially, then took it out as it made the post less readable).
Nice post - thanks for taking the trouble to write this, and make figures!
The NBS has other counter-intuitive properties, such as the that extra solutions can make some players worse off.
Why would that be counter-intuitive? Saying that is counter-intuitive implies that you should choose the max-min solution (the solution with the max over players P of(min(utility(P)) ).
Hence the KSBS replaces the independence requirement with "if one adds an extra option that is not better than either player's best option, this makes no player worse off".
You need to explain what "better" means in this context. Better for both players? With a sum or product that is higher? I can't think of any meaning that makes sense.
Another way to formulate the KSBS is by renormalising the utilities so that d=(0,0), u=(1,1), and then choosing the egalitarian solution:
What defines "the egalitarian solution"?
Thought-dump:
The common case: each player has a relatively smooth payoff over time, with the component from the outcome relatively unchanging and the component from the opportunity costs of negotiation cumulatively increasing and those components fairly factorizable.
If either estimates their negotiation cost rapidly swamping their outcome payoff they can agree to whatever the other has offered.
If either has a way of estimating that their ratio of outcome payoff differential / cumulative negotiation costs is significantly lower than the other's, and can reliably provide the other with a similar estimation capability, they will provide it and the disadvantaged can agree to stop negotiating. If they both can already estimate and have common knowledge of their capability and accuracy, the disadvantaged can agree to stop negotiating.
If they are in a society of similar agents, society can develop a stigma for prolonging negotiation for personal gain, making negotiation costs much higher than the usual time+energy required to negotiate, providing impetus for everyone to adopt some common procedure that benefits someone "more than" the other, but kind of at random or at least unpredictably.
An extreme case: We're in a True Prisoner's Dilemma and the payoff differential is significantly more than anything we could expect to do with our time+energy+negentropy+whateverresources. Also we're a superintelligence with all the resources of our lightcone. Also we don't have access to their source code and we're certain they don't have access to ours. So we estimate P(they cooperate) however possible... for example simulate all possible multiverses (with shortcuts like discarding ones we prove can't reach this state) to see the sum of our priors on universes where we get this choice and our counterpart cooperates and hope there's enough mass on ones where there's not a lot of coincidence between our algorithm and our counterpart's to prove one option's better... or that we've solved the problem of logical uncertainty + choice already...
A less extreme case: our resources are instead bounded by how much more gain we get by "negotiating" (computing) further, so we have to abstract more than we did in the above simulation+shortcuts, which means our program's a lot shorter and there will be far more coincidence between our algorithm and our counterpart's if they too are getting bounded... maybe we can estimate how much their computation costs them relative to their gain? Or how much they think our computation costs us relative to our gain?
If you google for "Nash Program", perhaps with the additional name "Rubinstein", and then read some of the articles listed there, you will learn that some of the ideas appearing in your "thought dump" are already pretty standard and have been explored quantitatively.
Has anyone dealt with bargaining games where different pure solutions cannot be linearly combined (i.e. a non-convex solution space)?
The direct answer is "yes", as you might have discovered by googling.
But different pure solutions can always be linearly combined - at least if the combination is supposed to be an expected utility rather than a guaranteed utility.
In an American football game, a coin is flipped at the start to produce a fair linear combination of "kicking off" and "receiving".
as you might have discovered by googling.
But if dclayh had used google instead of asking the question in a comment, you never would have had the opportunity to respond with your point about expected utility.
Asking in a comment could also attract the interest of others who might not have thought to ask that question, and gives others the opportunity to give their own answer or link to a resource they think is particularly good, that they might be able to answer follow up questions about.
I know this is a silly question, but do you know the figures you are presenting may be equated to the forces produced by the action of wind on a sail?
Your romantic dinner is a distance away, and I hope you are not following Achilles after the Tortoise.
This post looks at some of the current models for how two agents can split the gain in non-zero sum interactions. For instance, if you and a buddy have to split £10 between the two of you, where the money is discarded if you can't reach a deal. Or there is an opportunity to trade your Elvis memorabilia for someone's collection of North Korean propaganda posters: unless you can agree to a way of splitting the gain from trade, the trade won't happen. Or there is the stereotypical battle of the sexes: either a romantic dinner (RD) or a night of Battlestar Galactica (BG) is on offer, and both members of the couple prefer doing something together to doing it separately - but, of course, each one has their preference on which activity to do together.
Unlike standard games such as Prisoner's Dilemma, this is a coordinated game: the two agents will negotiate a joint solution, which is presumed to be binding. This allows for such solutions as 50% (BG,BG) + 50% (RD,RD), which cannot happen with each agent choosing their moves independently. The two agents will be assumed to be expected utility maximisers. What would your feelings be on a good bargaining outcome in this situation?
Enough about your feelings; let's see what the experts are saying. In general, if A and C are outcomes with utilities (a,b) and (c,d), then another possible outcome is pA + (1-p)C (where you decide first, with odds p:1-p, whether to do outcome A or C), with utility p(a,b) + (1-p)(c,d). Hence if you plot every possible expected utilities in the plane for a given game, you get a convex set.
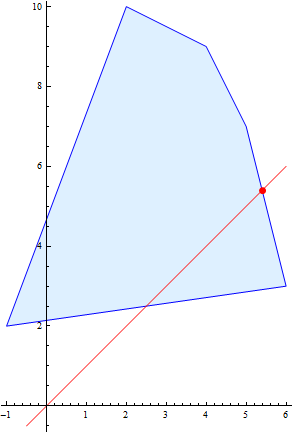
For instance, if there is an interaction with possible pure outcomes (-1,2), (2,10), (4,9), (5,7), (6,3), then the set of actual possible utilities is the pentagon presented here:
The points highlighted in red are the Pareto-optimal points: those where there is no possibility of making both players better off. Generally only Pareto-optimal points are considered valid negotiation solutions: any other point leaves both player strictly poorer than they could be.
The first and instinctive way to choose an outcome is to select the egalitarian point. This is the Pareto-optimal point where both players get the same utility (in this instance, both get 27/5 utility):
However, you can add an arbitrary number to your utility function without changing any of your decisions; your utility function is translation invariant. Since both players can do so, they can translate the shape seen above in any direction in the plane without changing their fundamental value system. Thus the egalitarian solution is not well-defined, but an artefact of how the utility functions are expressed. One can move it to any Pareto-optimal point simply with translations. Thus the naive egalitarian solution should be rejected.
Another naive possibility is to pick the point that reflects the highest total utility, by adding the two utilities together. This gives the vertex point (4,9):
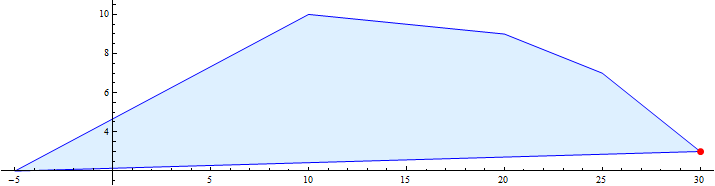
This method will select the same outcome, no matter what translation is applied to the utilities. But this method is flawed as well: if one agent decides to multiply their utility function by any positive real factor, this does not change their underlying algorithm at all, but does change the "highest total utility". If the first agent decides to multiply their utility by five, for instance, we have the new picture portrayed here, and the "highest total utility point" has decidedly shifted, to the first player's great advantage:
To summarise these transformations to utility functions, we say that a utility function is defined only up to affine transformations - translations and scalings. Thus any valid method of bargaining must also be invariant to affine transformations of both the utility functions.
The two most popular ways of doing this are the Nash Bargaining solution (NBS), and the Kalai-Smorodinsky Bargaining Solution (KSBS). Both are dependent on the existence of a "disagreement point" d: a point representing the utilities that each player will get if negotiations break down. Establishing this disagreement point is another subject entirely; but once it is agreed upon, one translates it so that d=(0,0). This means that one has removed the translation freedom from the bargaining game, as any translation by either player will move d away from the origin. In this example, I'll arbitrarily choose the disagreement at d=(-1,4); hence it now suffices to find a scalings-invariant solution.
Nash did so by maximising the product of the (translated) utilities. There are hyperbolas in the plane defined by the sets of (x,y) such that xy=a; Nash's requirement is equivalent with picking the outcome that lies on the hyperbola furthest from the origin. The NBS and the hyperbolas can be seen here:
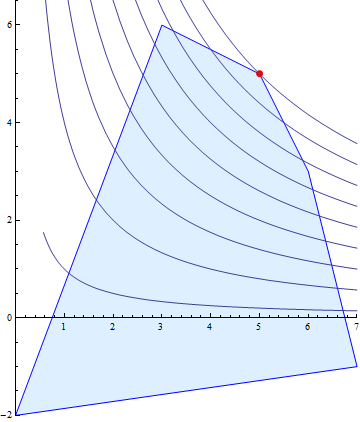
This gives the NBS as (4,9). But what happens when we scale the utilities? This is equivalent to multiplying x and y by constant positive factors. This will change xy=a to xy=b, thus will map hyperbolas to hyperbolas. This also does not change the concept of "furthest hyperbola from the origin", so the NBS will not change. This is illustrated for the scalings x->(18/25)x and y->(19/18)y:
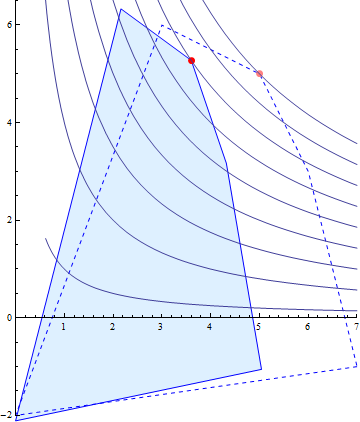
The NBS has the allegedly desirable property that it is "Independent of Irrelevant Alternatives". This means that if we delete an option that is not the NBS, then the NBS does not change, as can be seen by removing (2,10):
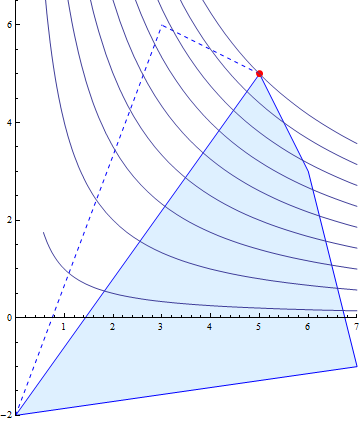
Some felt that "Independence of Irrelevant Alternatives" was not a desirable property. In the above situation, player 2 gets their best option, while player 1 got the worse (Pareto-optimal) option available. Human intuition rebels against "bargaining" where one side gets everything, without having to give up anything. The NBS has other counter-intuitive properties, such as the that extra solutions can make some players worse off. Hence the KSBS replaces the independence requirement with "if one adds an extra option that is not better than either player's best option, this makes no player worse off".
The KSBS is often formulated in terms of "preserving the ratio of maximum gains", but there is another, more intuitive formulation. Define the utopia point u=(ux, uy), where ux is the maximal possible gain for player 1, and uy the maximal possible gain for player 2. The utopia point is what a game-theory fairy could offer the players so that each would get the maximal possible gain from the game. Then the KSBS is defined as the Pareto-optimal point on the line joining the disagreement point d with the utopia point u:
Another way to formulate the KSBS is by renormalising the utilities so that d=(0,0), u=(1,1), and then choosing the egalitarian solution:
In a subsequent post, I'll critique these bargaining solutions, and propose a more utility-maximising way of looking at the whole process.