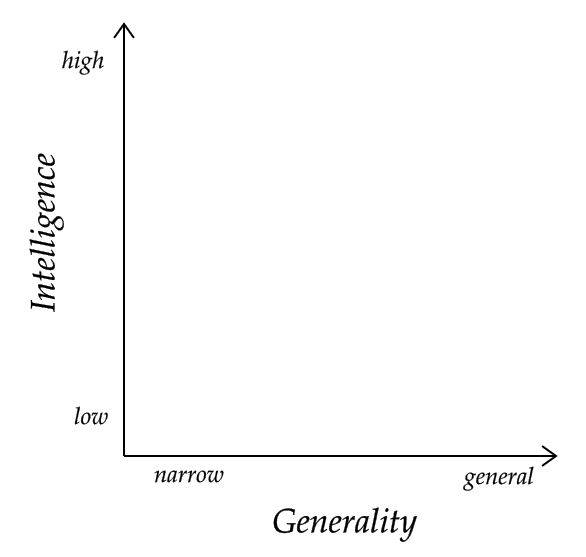
Are Intelligence and Generality Orthogonal?
5Alexander
2cubefox
6Alexander
4Alexander
1[anonymous]
4Alexander
1[anonymous]
4Alexander
5Shmi
-1[anonymous]
5Shmi
-1[anonymous]
2JBlack
3cubefox
2tailcalled
1cubefox
New Comment
I imagine the relationship differently. I imagine a relationship between how well a system can perform a task and the number of tasks the same system can accomplish.
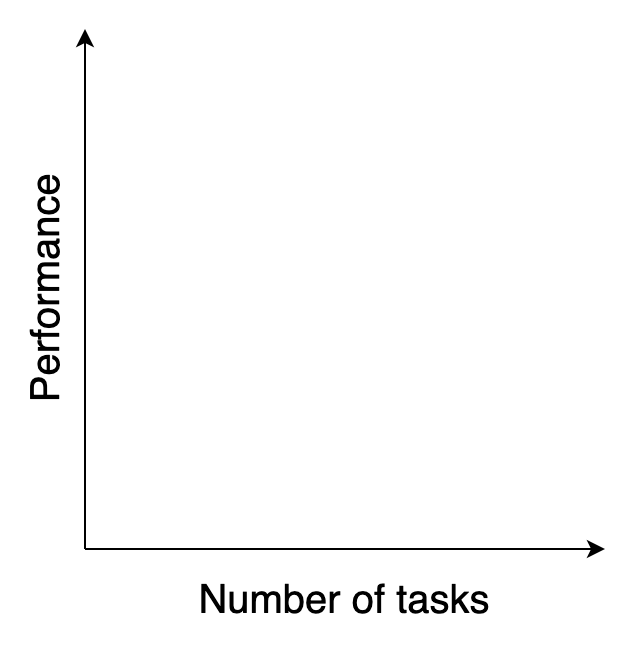
Does a chicken have a general intelligence? A chicken can perform a wide range of tasks with low performance, and performs most tasks worse than random. For example, could a chicken solve a Rubik's Cube? I think it would perform worse than random.
Generality to me seems like an aggregation of many specialised processes working together seamlessly to achieve a wide variety of tasks. Where do humans sit on my scale? I think we are pretty far along the x axis, but not too far up the y axis.
For your orthogonality thesis to be right, you have to demonstrate the existence of a system that's very far along the x axis but exactly zero on the y axis. I argue that such a system is equivalent to a system that sits at zero in both the x and y axes, and hence we have a counterexample.
Imagine a general intelligence (e.g. a human) with damage to a certain specialised part of their brain, e.g. short-term memory. They will have the ability to do a very wide variety of tasks, but they will struggle to play chess.
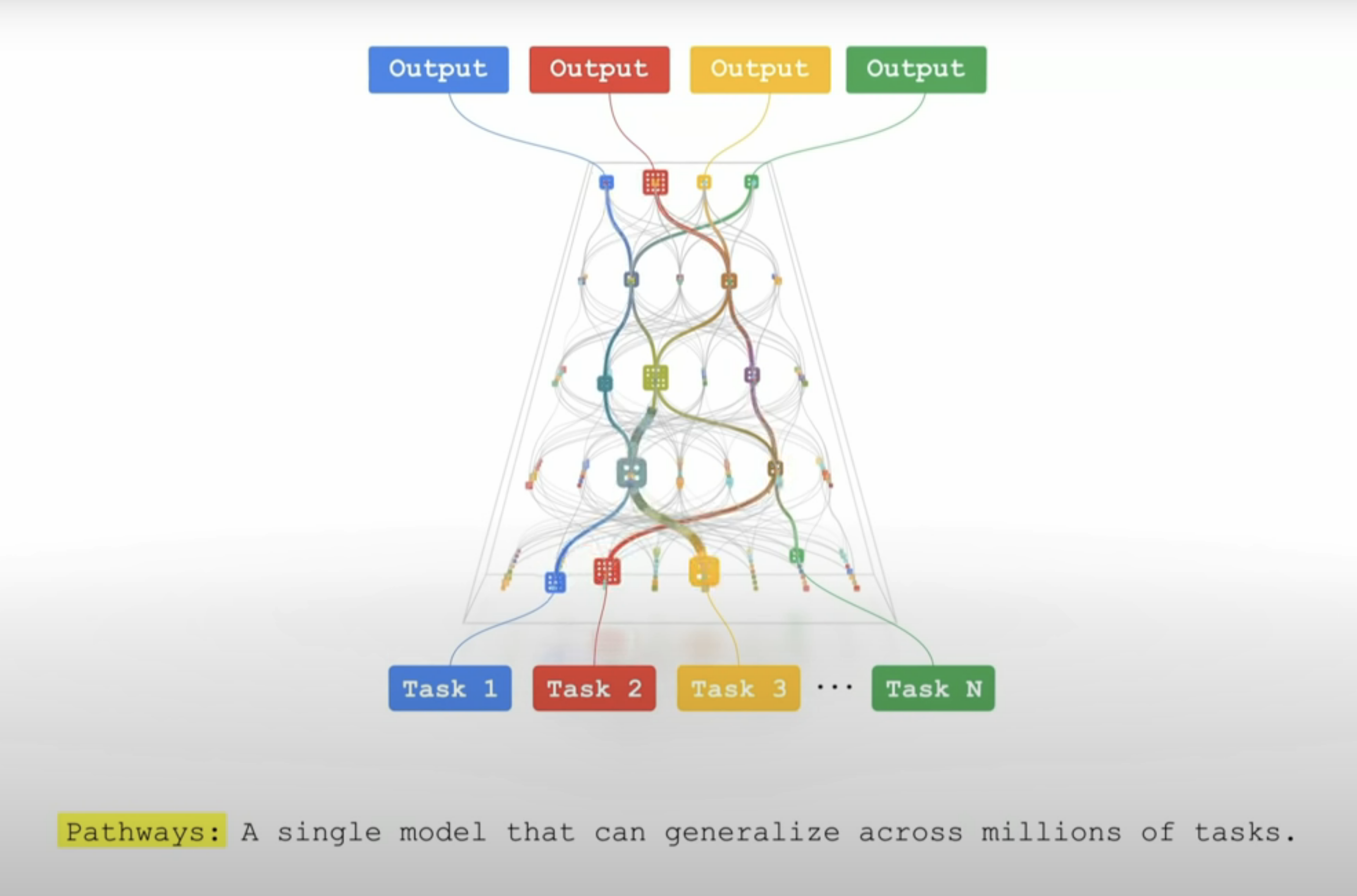
Jeff Dean has proposed a new approach to ML he calls System Pathways in which we connect many ML models together such that when one model learns, it can share its learnings with other models so that the aggregate system can be used to achieve a wide variety of tasks.
This would reduce duplicate learning. Sometimes two specialised models end up learning the same thing, but when those models are connected together, we only need to do the learning once and then share it.
If Turing Completeness turns out to be all we need to create a general intelligence, then I argue that any entity capable of creating computers is generally intelligent. The only living organism we know of that has succeeded in creating a computer is the humans. Creating computers seems to be some kind of intelligence escape velocity. Once you create computers, you can create more intelligence (and maybe destroy yourself and those around you in the process).
Regarding the counterexample: I think it is fair to say that perfect orthogonality is not plausible, especially not if we allow cases with one axis being zero, whatever that might mean. But intelligence and generality could be still largely orthogonal. What do you think of the case of insects, as an example of low intelligence and high generality?
(I think not even the original orthogonality thesis holds perfectly. An example is the oft-cited fact that animals don't optimize for the goal of inclusive genetic fitness because they are not intelligent enough to grasp such a goal. So they instead optimize for similar things, like sex.)
Have you come across the work of Yann LeCun on world models? LeCun is very interested in generality. He calls generality the "dark matter of intelligence". He thinks that to achieve a high degree of generality, the agent needs to construct world models.
Insects have highly simplified world models, and that could be part of the explanation for the high degree of generality exhibited by insects. For example, the fact the male Jewel Beetle fell in love with beer bottles mistaking them for females is strong evidence that beetles have highly simplified world models.

I see what you mean now. I like the example of insects. They certainly do have an extremely high degree of generality despite their very low level of intelligence.
We can demonstrate this wth a test.
- Get a Rubik's Cube playing robotic arm, and ask it to flip a shuffled Rubik's Cube randomly until it's solved. How many years will it take until it's solved? It's some finite time, right? Millions of year? Billions of years?
- Get a chicken and give it a Rubik's Cube and ask it to solve it. I don't think it will perform better than our random robot above.
I just think that randomness is a useful benchmark for performance on accomplishing tasks.
In Bogosort, the lower bound for random version is unbounded which is O(inf). You can even turn the Rubiks Cube problem into a sorting problem of finding path from starting position to solved position, involving a series of moves. I'm not sure if there are more than one set of shortest path solution to each scenario.
Oh, I'm not making the argument that randomly permuting the Rubik's Cube will always solve it in a finite time, but that it might. I think it has a better chance of solving it than the chicken. The chicken might get lucky and knock the Rubik's Cube off the edge of a cliff and it might rotate by accident, but other than that, the chicken isn't going to do much work on solving it in the first place. Meanwhile, randomly permuting might solve it (or might not solve it in the worst case). I just think that random permutations have a higher chance of solving it than the chicken, but I can't formally prove that.
"A specialist is like a boil: its fullness is one-sided" -- Kozma Prutkov
A (semi-fictional) example that comes to mind is the protagonist of Rain man, and similar idiot savant stereotypes.
I think a better approach would be not black and white orthogonality, but the degree of correlation. In humans there is definitely a variety of specialization at high intelligence levels (e.g. there are polymaths like Feynman who can excel in many disparate activities to the degree an average human would not, but also those who only excel in one area, say, music, and suck at life in general), but also hints that smarter people are on average smarter in multiple areas. There are probably studies out there that research correlation between intelligence and specialization, I wonder if you did a literature review?
I think what people mean by intelligence is how well someone or something does on tests, stuff you measure with precision and recall. Then you do some arithmetic and you get a number, whether it's how many pieces of music you wrote or how many answers you got correct. Anything about intelligence outside of this context is actually a misnomer. They are rather talking about the process where the measure of intelligence can be deduced. A lot of it is dependent on the measurement of speed. That's why they usually give you time limit for shit like this.
I think you have it backwards. Tests measure or purport to measure intelligence, but most people can tell a smart person from a not so smart one, though this can vary by domain.
Since intelligence is an arbitrary value on completely different processes in different context, I don't know if you can call tests a measurement of such construct. Generally, it's mostly a measure of 1) good memory and 2) the speed of the look up. If you have good memory but slow, you won't be able to make practical use of the good memory, or at least maximizing its potential. If you have shit memory but fast look up, then you can specialize and do that for the rest of your life and be good at it, improving your look up time over the years. 3) The next layer is measuring the quality of the look up. 1 is dataset, 2 is running time, 3 is tuning the weights.
The term intelligence bears no actual meaning without some form of concrete measurement.
I think there are two interesting questions relating to this:
- Are there any seemingly narrow tasks that are fully general in the sense that the ability to perform such a task requires, and implies, being able to generalize to some minimal level of performance on all tasks that we could classify as intelligence-related?
- We have seen performance beyond - and even incredibly far beyond - human performance on various narrow intelligence-related tasks. Is there generality far beyond human generality? In particular do humans actually have huge blind spots that even an otherwise sub-human AI might be able to exploit in the real world?
Sorry - forgot about your comment.
-
Tasks that animals usually face? (Find food, a safe place to sleep, survive, reproduce ...)
-
This is an intriguing question. My first intuition: Probably not, because ...
- It seems evolution would have figured it out by now. After all, evolution optimizes heavily for generality. Any easily fixable blind spot would be a low hanging fruit for natural selection (e.g. by being exploited in inter-species competition).
- The level of generality of most animals seems very similar, and seems to have stayed similar for a very long time. Even the case of humans with apparently unusually high generality is, if the point in my post was right, not actually a case of unusually high generality, just a case of unusually high intelligence.
- More specifically: Generality seems to be strongly related to having a "real-world domain" (see Arbital link in the post), which even quite simple animals already satisfy. It is not clear what could be more general than that.
On the other hand, perhaps there is indeed a higher level of generality, just not one which is a low-hanging fruit. Or one which is at least not a low-hanging fruit for the neuron-based brain structure which evolution on Earth is using in animals. (For example, brains are highly parallel but very slow in serial tasks, while silicon processors have a much higher serial speed. From computational complexity theory it is known that not all algorithms can be parallelized efficiently.)
Another possibility is that some higher level of generality simply needs a certain amount of intelligence in order to "work". Which would mean that at some point in increasing intelligence, a phase-transition to a higher generality level would occur. The reason this has not happened yet in the history of evolution would simply be that a sufficient level of intelligence was not yet achieved.
Thinking of it, one possible example for the latter having already happened once could be: cultural evolution. Only humans can (due to language, but also due to high intelligence) accumulate information across generations, learn, and adapt via culture instead of just via genes. That would indeed contradict my theory that humans are not significantly more general than other animals. If we accept the emergence of cultural evolution in humans as a phase transition to a higher level of generality, then there could be still other levels, inaccessible to us, but possibly accessible to a highly intelligent AI.
Edit: Actually there were at least two phase transitions in "learning methods" of the above kind: Once via the emergence of cultural evolution some hundred thousand years ago, and once via the emergence of brains some hundred million years ago. If evolution is already some kind of learning process, then organisms with brains add one layer, and our "cultural" layer is a further one on top.
But classical chess computers like DeepBlue rely a lot on raw compute, yet this brute force approach is fairly useless in cases with large search space, like Go. I think the number of parameters in a neural network would be a better approximation.
Then we can even make the scaling hypothesis more precise: Presumably it says scaling is enough for (more) intelligence_1, but not for generality.