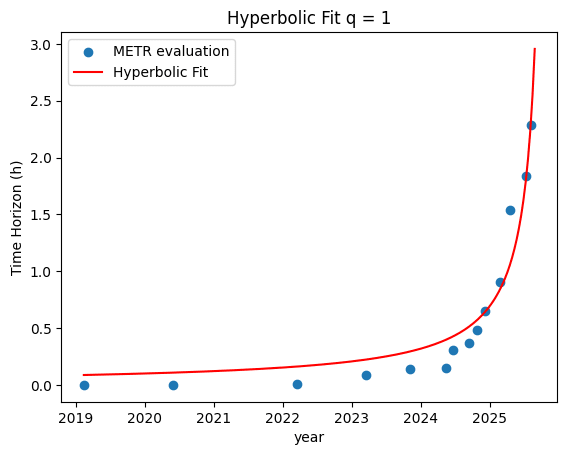
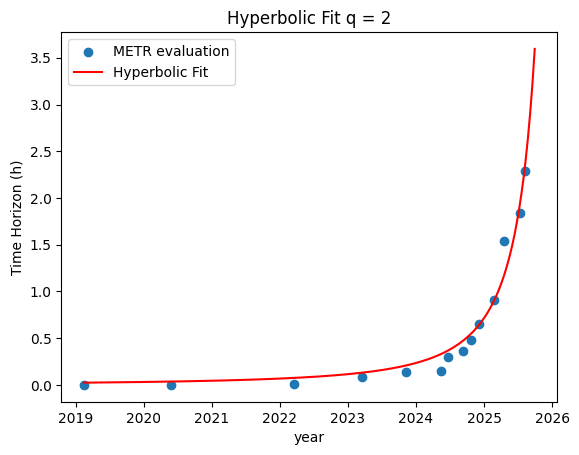
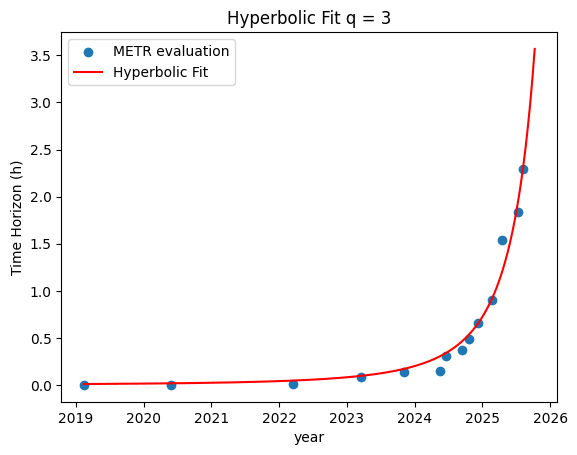
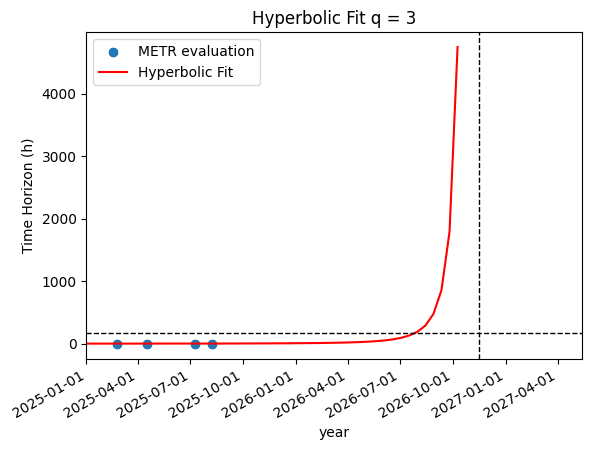
Hyperbolic trend with upcoming singularity fits METR capabilities estimates.
17gjm
9Valentin2026
6gjm
3ryan_greenblatt
4gjm
2Nikola Jurkovic
New Comment
The code in your notebook does its hyperbolic fitting by (nonlinear) least squares on the original data, but its exponential fitting by (linear) least squares on the log of the original data.
This means (1) that your exponential fit will look worse "on the right" where the numbers are larger than an actual least-squares fit of an exponential, and (2) it will have worse mean squared error (on the original data) than an actual least-squares fit of an exponential.
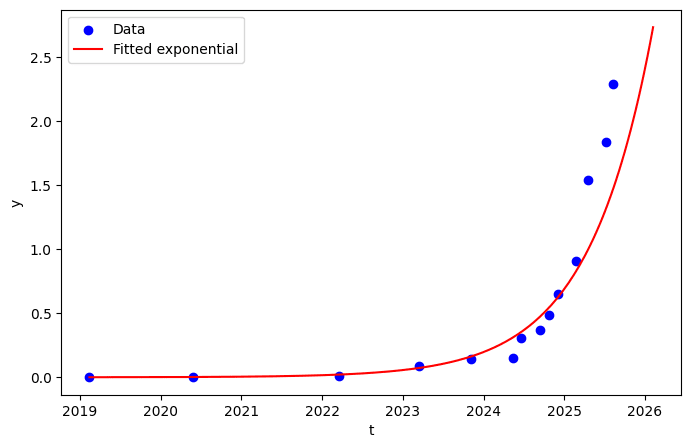
When I do an exponential fit using the same machinery as you used for your hyperbolic fit, I get this graph
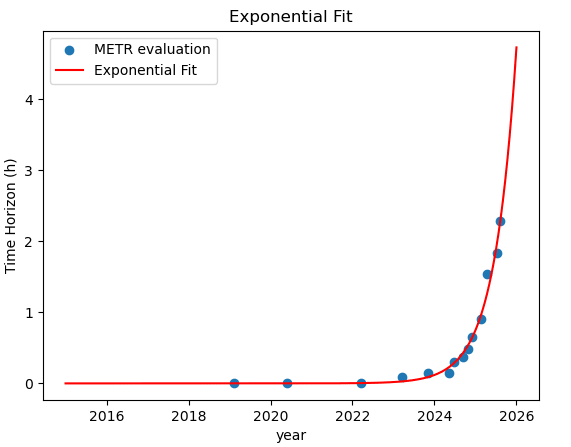
and a "total error" of 0.107 versus 0.141 for the q=2 hyperbolic fit.
[EDITED to add:] The specific exponential I get, in case anyone wants to check, is horizon = exp b (t-t0) where b = 1.8421 and t0 is 2025-02-27.
[EDITED to add:] I've strong-downvoted the post, not because I think there's anything very terrible about making the mistake I believe you made, but because at first glance it looks like evidence for something important and I think it isn't in fact evidence for that important thing and I don't want people to be misled.
[EDITED again to add:] Full post at https://www.lesswrong.com/posts/ZEuDH2W3XdRaTwpjD/hyperbolic-model-fits-metr-capabilities-estimate-worse-than
Thanks for checking, confirming, and editing accordingly. I reiterate that despite my criticisms of the content, this is what epistemic virtue looks like: write things in such a way that others can check them, and correct appropriately if they turn out to have been wrong.
(Strong-downvote undone since with the corrections at the top the OP is no longer likely to mislead anyone much.)
Are you looking at mean squared error in log space? I expect this will be more meaningful and less dominated by the last few points.
It's in linear space for the hyperbolic model and in log space for the exponential one, which unfortunately means all the comparisons are invalid. See my comment (and the longer post linked from it).
Thanks for the post!
Nikola Jurkovic suggests that as soon as model can do a month-long task with 80% accuracy, it should be able to do any cognitive human task
I didn't mean to suggest this in my original post. My claim was something more like "a naive extrapolation means that 80% time horizons will be at least a month by the end of the decade, but I think they'll be much higher and we'll have AGI"
Curated and popular this week