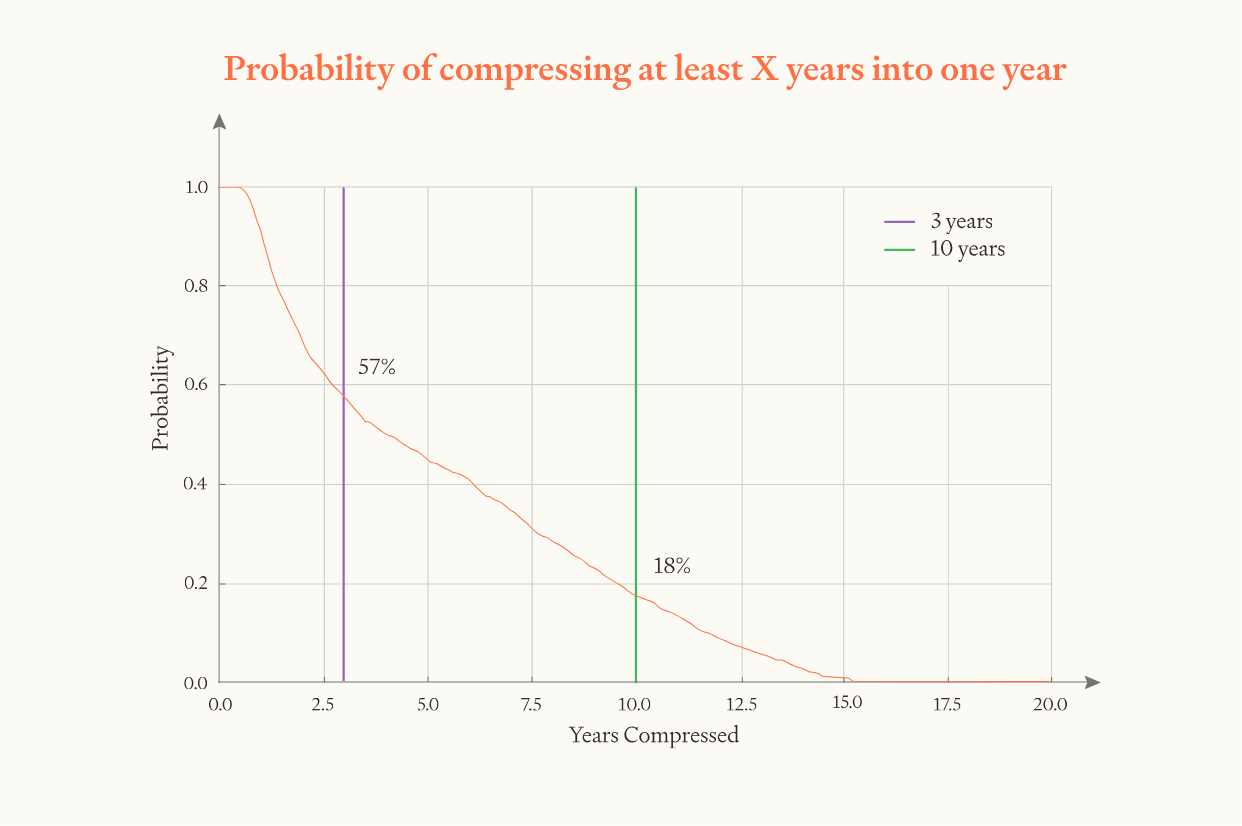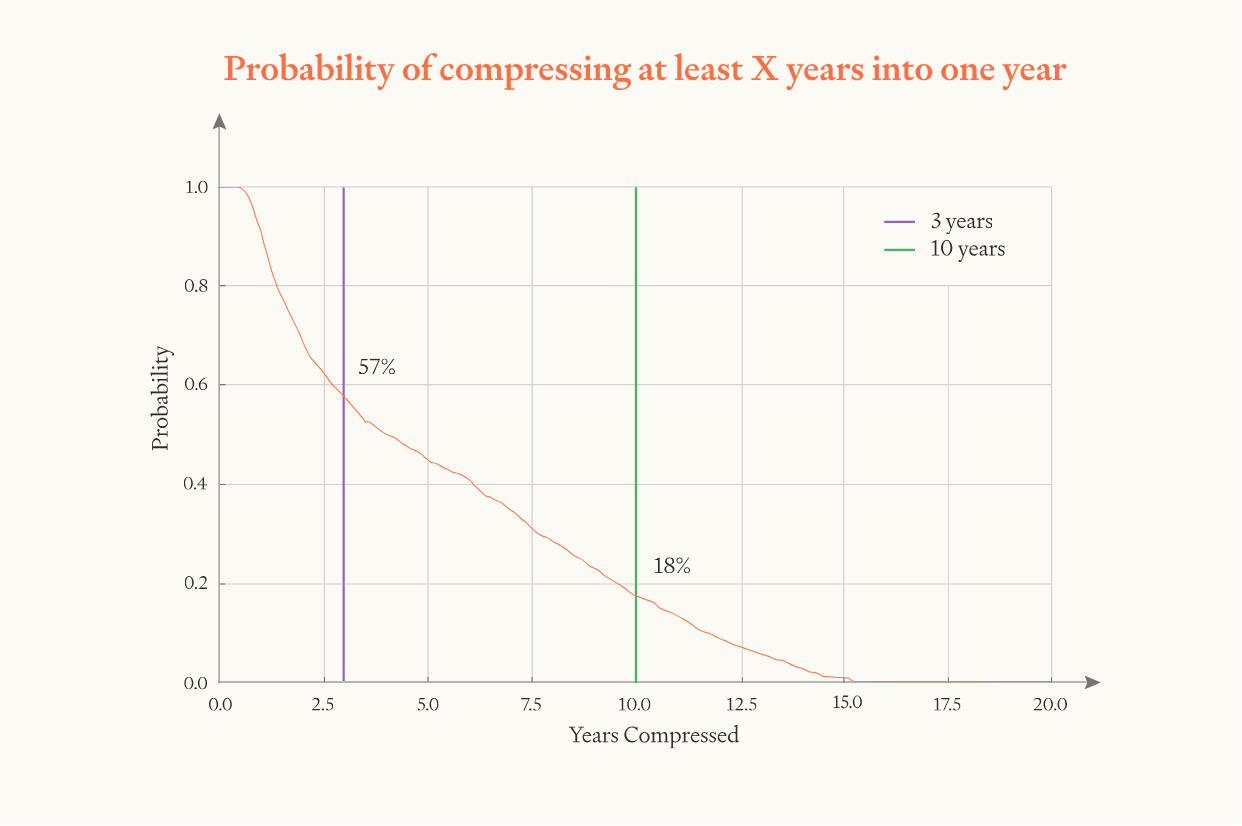How quick and big would a software intelligence explosion be?
21Adam Scholl
9Tom Davidson
16Adam Scholl
7Tom Davidson
15Adam Scholl
8Tom Davidson
4dr_s
2Tom Davidson
6dr_s
2Lukas Finnveden
13Lukas Finnveden
6Tom Davidson
13jake_mendel
3Tom Davidson
3Jacob Pfau
2Tom Davidson
6Daniel Kokotajlo
4Tom Davidson
3Daniel Kokotajlo
2Tom Davidson
4Lukas Finnveden
4Tom Davidson
3Oliver Sourbut
2reallyeli
3Tom Davidson
1reallyeli
1reallyeli
2Tom Davidson
1[comment deleted]
New Comment
This model strikes me as far more detailed than its inputs are known, which worries me. Maybe I’m being unfair here, I acknowledge the possibility I’m misunderstanding your methodology or aim—I’m sorry if so!—but I currently feel confused about how almost any of these input parameters were chosen or estimated.
Take your estimate of room for “fundamental improvements in the brain’s learning algorithm,” for example—you grant it's hard to know, but nonetheless estimate it as around “3-30x.” How was this range chosen? Why not 300x, or 3 million? From what I understand the known physical limits—e.g., Landauer's bound, the Carnot limit—barely constrain this estimate at all. I'm curious if you disagree, or if not, what constrains your estimate?
This model strikes me as far more detailed than its inputs are known
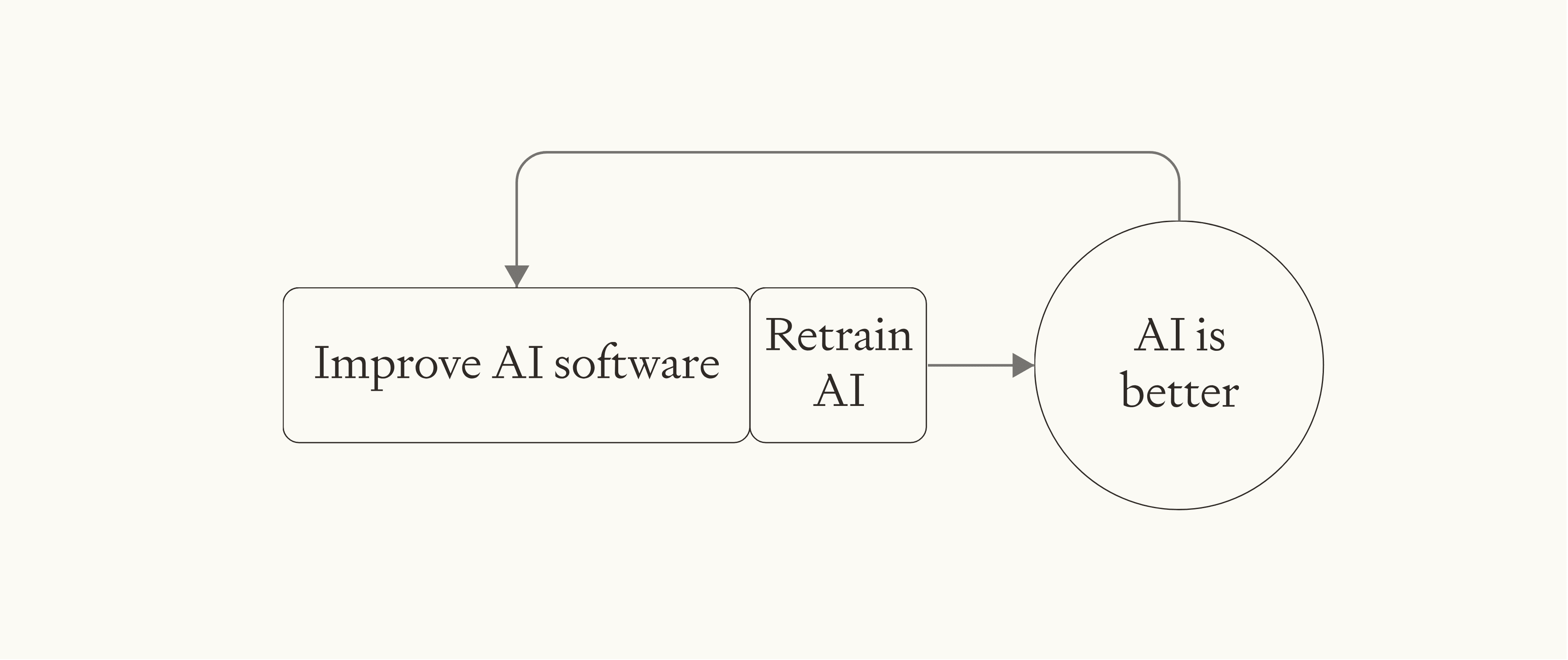
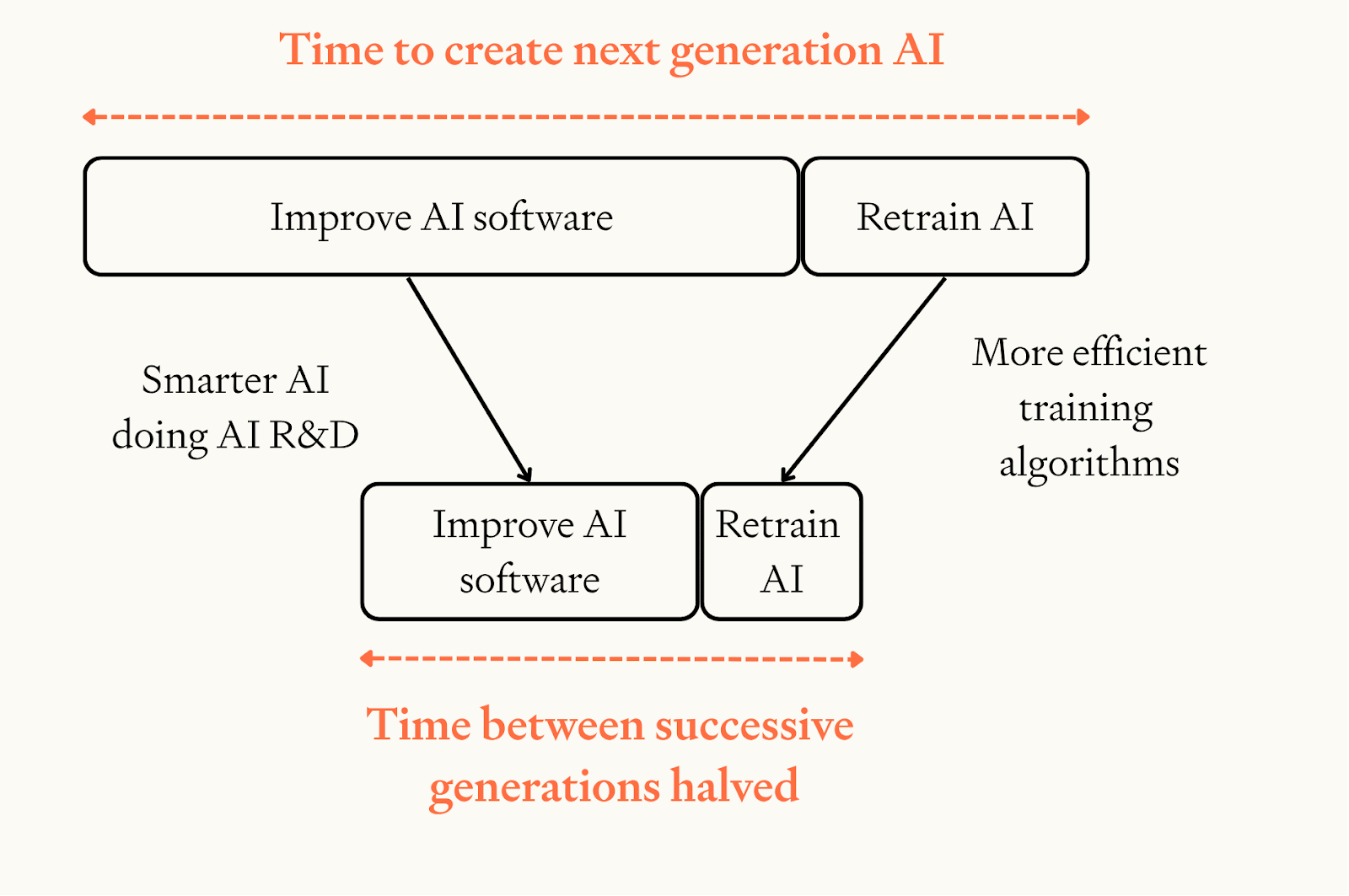
The model is very simple. Literally four lines of code:
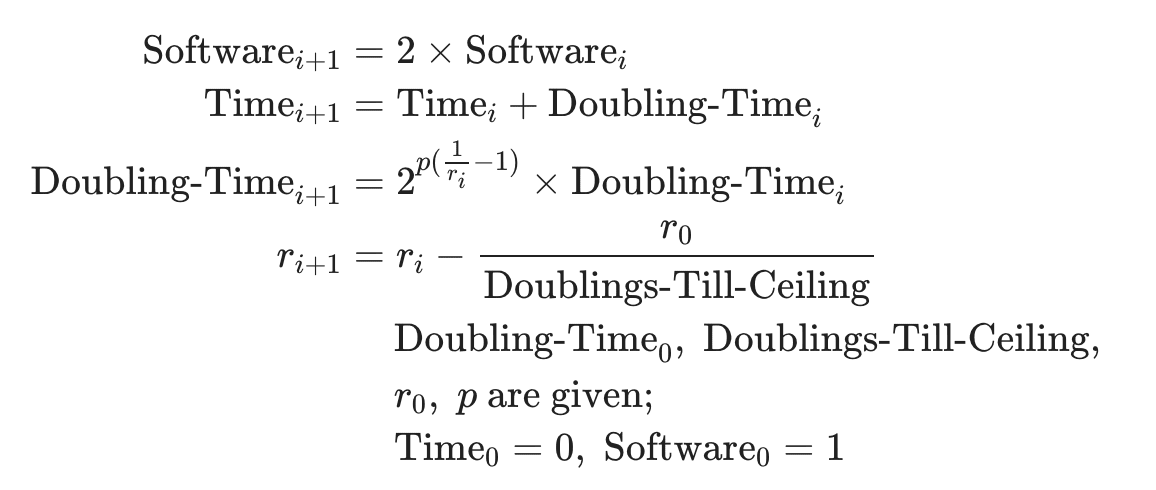
This post is long, but it's not long because it's describing a complicated model. It's long because it's trying to estimate the inputs as well as possible.
Take your estimate of room for “fundamental improvements in the brain’s learning algorithm,” for example—you grant it's hard to know, but nonetheless estimate it as around “3-30x.”
Yeah I think you've honed in on exactly the right subpart here. This is essentially the "and all other possible improvements" part of the estimate of the distance to ultimate limits, which is especially ungrounded.
Some of the other parts of the "distance to limits" section focus on specific improvements that are a bit easier to roughly ballpark. But one reviewer pointed out that there could be further fundamental improvements, which seemed right to me, and I wanted to avoid being biased in the conservative direction by not including it.
My basic methodology for this section was to interview various people about ways in which efficiency could improve beyond the brain level and how big they guessed these gains would be, and then have ppl review the results. But, as I say in the paper multiple times, the estimates for effective limits are especially speculative.
So I think it's totally fair to say: the uncertainty on this param is way bigger than what's you've done in your Monte Carlo, you should have a much wider range and so put more probability on really dramatic intelligence explosions. E.g. Lukas Finnveden makes a similar point in another comment.
But I don't think of this as a flaw in the model:
- It's just true of reality that there's a lot of uncertainty about the distance for effective limits for software, and it's just true of reality that that translates into a lot of uncertainty about how big an SIE might be. So it seems like the model's doing a good job in capturing that.
- And yes, I think i've probably underestimated the extent of this uncertainty in this analysis.
- As I said above, the model isn't complicated. So there's not some problem of fitting a model with lots of gears and surprising interaction effects to multiple params that have massive uncertainties, resulting in predictions that we don't know where they came from. The model inputs flow through to the bottom line in ways that are very simple and transparent. Lukas has another comment that does a good job of explaining this.
Fwiw, I think it could be possible to substantially improve upon my estimates of the effective limits param but spending a week researching and interviewing experts. I'd be excited for someone to do that!
I agree the function and parameters themselves are simple, but the process by which you estimate their values is not. Your paper explaining this process and the resulting forecast is 40 pages, and features a Monte Carlo simulation, the Cobb-Douglas model of software progress, the Jones economic growth model (which the paper describes as a “semi-endogenous law of motion for AI software”), and many similarly technical arcana.
To be clear, my worry is less that the model includes too many ad hoc free parameters, such that it seems overfit, than that the level of complexity and seeming-rigor is quite disproportionate to the solidity of its epistemic justification.
For example, the section we discussed above (estimating the “gap from human learning to effective limits”) describes a few ways ideal learning might outperform human learning—e.g., that ideal systems might have more and better data, update more efficiently, benefit from communicating with other super-smart systems, etc. And indeed I agree these seem like some of the ways learning algorithms might be improved.
But I feel confused by the estimates of room for improvement given these factors. For example, the paper suggests better “data quality” could improve learning efficiency by “at least 3x and plausibly 300x.” But why not three thousand, or three million, or any other physically-possible number? Does some consideration described in the paper rule these out, or even give reason to suspect they’re less likely than your estimate?
I feel similarly confused by the estimate of overall room for improvement in learning efficiency. If I understand correctly, the paper suggests this limit—the maximum improvement in learning efficiency a recursively self-improving superintelligence could gain, beyond the efficiency of human brains—is "4-10 OOMs," which it describes as equivalent to 4-10 "years of AI progress, at the rate of progress seen in recent years."
Perhaps I’m missing something, and again I'm sorry if so, but after reading the paper carefully twice I don’t see any arguments that justify this choice of range. Why do you expect the limit of learning efficiency for a recursively self-improving superintelligence is 4-10 recent-progress-years above humans?
Most other estimates in the paper seem to me like they were made from a similar epistemic state. For example, half the inputs to the estimate of takeoff slope from automating AI R&D come from asking 5 lab employees to guess; I don't see any justification for the estimate of diminishing returns to parallel labor, etc. And so I feel worried overall that readers will mistake the formality of the presentation of these estimates as evidence that they meaningfully constrain or provide evidence for the paper’s takeoff forecast.
I realize it is difficult to predict the future, especially in respects so dissimilar from anything that has occurred before. And I think it can be useful to share even crude estimates, when that is all we have, so long as that crudeness is clearly stressed and kept in mind. But from my perspective, this paper—which you describe as evaluating “exactly how dramatic the software intelligence explosion will be”!—really quite under-stresses this.
Hi,
I agree the function and parameters themselves are simple, but the process by which you estimate their values is not. Your paper explaining this process and the resulting forecast is 40 pages, and features a Monte Carlo simulation, the Cobb-Douglas model of software progress, the Jones economic growth model (which the paper describes as a “semi-endogenous law of motion for AI software”), and many similarly technical arcana.
Could you explain why you think it's bad if the "process by which I estimate parameter values" is too complex? What specific things were overly complex?
The specific things you mention don't make sense to me.
the resulting forecast is 40 pages,
(Fwiw, it's 20-25 pages excluding figures and appendices)
To my mind, identifying a model with a small number of key params, and then carefully assessing each param from as many different angles as possible, is a good approach. Yes, I could have approached each param from fewer angles, but that would make the overall estimate less robust.
Monte Carlo simulation
You surely know this, but running the Monte Carlo simulation doesn't add complexity to the process of estimating the values (given that i'm estimating ranges in any case). And it seems pretty useful to do given the massive uncertainty.
Cobb-Douglas model of software progress, the Jones economic growth model
The "Cobb-Douglas model" and the "Jones economic growth model" are the same thing, and used to derive the 4 line model mentioned above. Mentioning these terms doesn't add complexity to the process of estimating the params. Tbh, i'm confused and a bit frustrated at you calling me out for using these terms. The implict accusation that I'm using them to aggrandize my paper. But neither of these terms appear in the summary. They appear in the main body essentially the bare minimum number of times, I think once each. Would you prefer I didn't mention them these standard terms for (very simple!) math models?
and many similarly technical arcana
I basically think you're being unfair here, so want to challenge you to actually name these or retract.
... So that's my response to the charge that the param estimates are overly complicated. But I want to respond to one other point you make, that i'm v sympathetic to.
level of... seeming-rigor is quite disproportionate to the solidity of its epistemic justification
This feels like maybe more the core thing you're reacting to here.
I was worried about the paper coming off in this way. An earlier draft had more caveats and repeated them more often. Reviewers suggested I was being excessive. I'll take yours comments here as a sign that I should have ignored them.
But the paper is still very clear and explicit about its limitations.
Quote from the summary (that will be read way more than any references to "Cobb Douglas" or "Jones model") [bolded emphasis in the original]:
- "Our model is extremely basic and has many limitations"
- “Garbage in, garbage out”. We’ve done our best to estimate the model parameters, but there are massive uncertainties in all of them"
- A previous draft highlight the distance to limits here as an acute example - I think you're right about this
- "Overall, we think of this model as a back-of-the-envelope calculation. It’s our best guess, and we think there are some meaningful takeaways, but we don’t put much faith in the specific numbers."
I basically think you're being unfair here, so want to challenge you to actually name these or retract.
... So that's my response to the charge that the param estimates are overly complicated. But I want to respond to one other point you make
It sounds like we're talking past each other, if you think I'm making two different points. The concern I'm trying to express is that this takeoff model—by which I mean the overall model/argument/forecast presented in the paper, not just the literal code—strikes me as containing confusingly much detail/statistics/elaboration/formality, given (what seems to me like) the extreme sparsity of evidence for its component estimates.
the paper is still very clear and explicit about its limitations
I grant and (genuinely) appreciate that the paper includes many caveats. I think that helps a bunch, and indeed helps on exactly the dimension of my objection. In contrast, I think it probably anti-helped to describe the paper as forecasting "exactly how big" the intelligence explosion will be, in a sense constrained by years of research on the question.
It seems to me that demand for knowledge about how advanced AI will go, and about what we might do to make it go better, currently far outstrips supply. There are a lot of people who would like very much to have less uncertainty about takeoff dynamics, some of whom I expect might even make importantly different decisions as a result.
... and realistically, I think many of those people probably won't spend hours carefully reading the report, as I did. And I expect the average such person is likely to greatly overestimate the amount of evidence the paper actually contains for its headline takeoff forecast.
Most obviously, from my perspective, I expect most casual readers to assume that a forecast billed as modeling "exactly how big" the intelligence explosion might be, is likely to contain evidence about the magnitude of the explosion! But I see no evidence—not even informal argument—in the paper about the limits that determine this magnitude, and unless I misunderstand your comments it seems you agree?
I think it probably anti-helped to describe the paper as forecasting "exactly how big"
That's fair. I've removed the word "exactly" from the top of this paper. Edits will take a few days to process on the website version.
(I definitely didn't intend "exactly" to connote precision. I wanted to highlight that the paper was focussed on the extent of the intelligence explosion, in contrast with our previous paper which argued that there could be accelerating progress but didn't analyse how big the resulting SIE might be. Some reviewers were confused at the contrast. For the tweet, I think i was also subconsciously imitating the first tweet of AI-2027 which said "How, exactly, could AI take over by 2027". But I agree the word "exactly" here could easily be misread as implying the paper gives precise results, which is an oversight.)
Fwiw, the results table gives the results to 1 sig fig and uses "~" repeatedly to avoid the impression of false precision. And the paper explicitly says "While the exact numbers here are obviously not to be trusted...", before giving what I believe are more robust takeaways. In the discussion opens with "If this analysis is right in broad strokes" (emphasis mine).
The twitter thread also said "It goes without saying: the model is very basic and has many big limitations" and "We estimate these three parameters through a mix of empirical evidence and guesswork". The lead tweet also said "This is my best stab at an answer", which i thought connoted an informal, modest and tentative answer. (emphasis mine)
This is all to say that, again, i'm sympathetic with the worry that people will overestimated the precision and accuracy of the analysis and made significant efforts to avoid this. Honestly, I'd guess I made greater efforts than most similarly-speculative posts in this reference class. That said, I suspect we still disagree a lot about the amount of signal in this analysis, which is probably coming into play here.
And I expect the average such person is likely to greatly overestimate the amount of evidence the paper actually contains for its headline takeoff forecast.
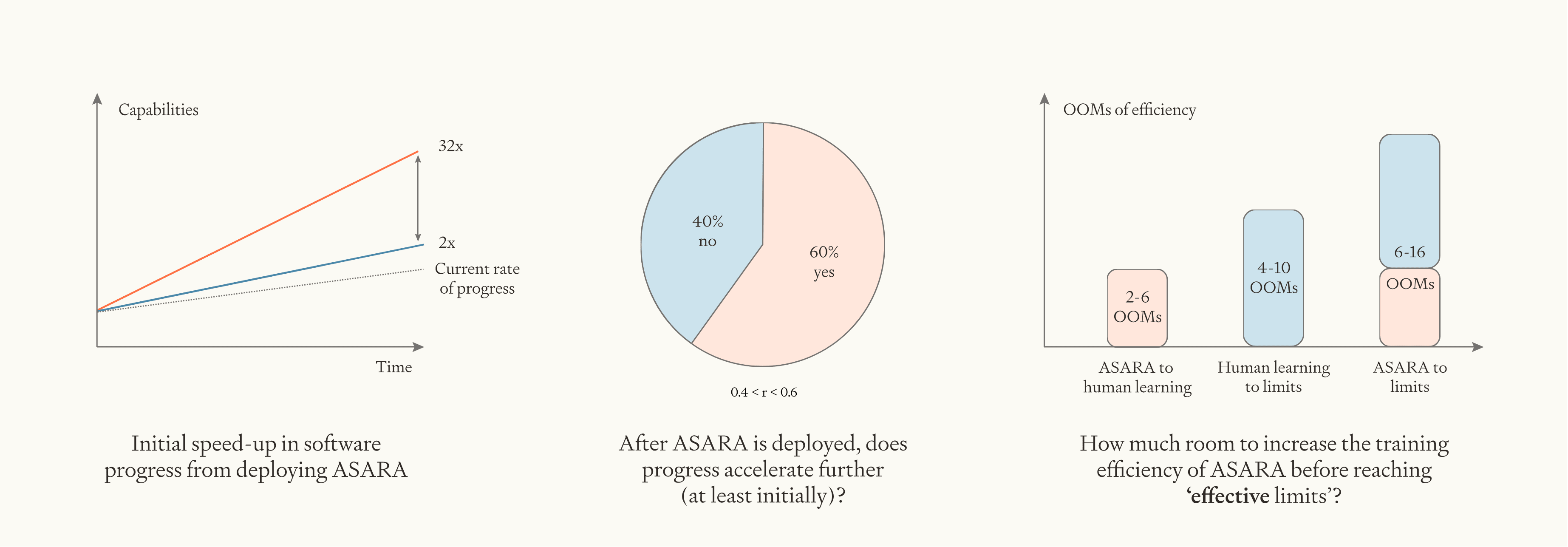
I think that this paper contains comparable or greater amounts of evidence to Yudkowsky's Intelligence Explosion Microeconomics, Bostrom's Superintelligence, and AI-2027's takeoff speed analysis. (In large part it contains this because I'm able to steal what I consider the most relevant insights from this previous work.) My own (biased!) opinion is that this is the best analysis we have on this question. It contains multiple angles on estimating the initial speed up from deplying ASARA, analysis of the value of r (which i think is hugely important), analysis of room to improve AI algs before matching humans, and some estimates/guesses at how much far certain improvements above human-level algs might go.
And it seems to me like you could level similar objections against previous these takeoff speeds analyses. Intelligence Explosion Microeconomics is also a paper, and it's name "microeconomics" suggests that it's going to do some empirically grounded mathematical modelling of the dynamics of recursive improvement. (I think it's a great paper!) AI-2027 placed probability distributions over their parameters and ran a Monte Carlo (I believe). Superintelligence is an academic-style book. I think my work has similar or more disclaimers about how speculative it is than these other pieces. I'm not knocking these papers! I'm just claiming that I don't think my paper is out of line of previous work in this regard.
I also think the evidential situation is here comparable (though probably more dire) to the evidence about AI timelines and AI alignment. The evidence doesn't really constrain reality very much. But ppl still publish best-guess estimates/analyses.
Still, I do agree that it's very easy for lay readers to overestimate how much evidence underpins the best analyses that the world has on these questions. The fact that this is even a paper puts it in a reference class of "papers", and most papers aren't about AGI-related stuff and are much less speculative. I felt this was at play with titotal's critique of AI-2027. My experience reading it was "yeah these objections aren't that surprising to me, what did expect from smg forecasting AGI and superintelligence". And this pushes towards being even more upfront about the limitations of the analysis.
I see no evidence—not even informal argument—in the paper about the limits that determine this magnitude, and unless I misunderstand your comments it seems you agree?
No i don't. I think the paper contains meaningful evidence about the magnitude.
First, evidence that r is quite plausibly already below 1. If so, the SIE won't last long. This makes is plausible that we get <3 years of progress.
Second, pointing out that 10 years of progress is ~10 OOMs of efficiency gains, which is a large amount relative to efficiency gains we've historically seen in ML, more than the total efficiency gains we've ever seen in many tech areas, and comparable to those we've ever seen in computing hardware. Even if r > 1 when we first develop ASARA, I think there's a good chance that it falls below 1 during the course of 10 OOMs of progress. (Especially given the possibility of compute bottlenecks kicking in as cognitive inputs are massively increased but compute increases much more slowly.)
Third, evidence about the gap from ASARA algs to human-level algs. If this gap had been much bigger or much smaller, that should update our beliefs about how long the SIE will go on for.
Fourth, somewhat-transparent quantitative estimates of some the factors that are additional alg gains above human-level. E.g. "brain is severely undertrained", "low fraction of data is relevant", "variation between humans". For these estimates, a reader can see roughly where the number is coming from.
Fifth, listing additional possible gains without transparent estimates of their quantitive size. Here, as I said, the process was speaking to people with relevant expertise and asking them to eye-ball/guess at the gain. So yes, these numbers are particularly untrustworthy! But to my mind they still contain some signal. It might have been that this process didn't uncover any significant improvements beyond the brain. In fact though, there are multiple plausibly-big improvements, which did significantly widen my personal credences on how big the IE might be. In hindsight, I should have put in more effort to making all these estimates transparent, and flagged more clearly how big this uncertainty is.
You could summarise this all as "no evidence about the limits" bc, for some of these factors, there's no explicit argument the factor isn't absolutely massive. So if you came in with a strong view that one factor was massive, you won't be much moved. But that misses that, for people in many epistemic situations, the five pieces of evidence i've just listed here will be informative.
Fyi, your comments have convinced me to add some additional qualifiers on this point:
- To the top of the paper, just before the summary, we'll add: Like all analyses of this topic, this paper is necessarily speculative. We draw on evidence where we can, but the results are significantly influenced by guesswork and subjective judgement.
- To the table cell on limits, we'll add: This involves a fair amount of guesswork and is a massive remaining uncertainty.
- To the section estimating limits, we'll add: some of the factors listed are plausibly even bigger than our upper estimate, e.g. “must satisfy physical constraints” and "fundamental improvements”.
The concern I'm trying to express is that this takeoff model—by which I mean the overall model/argument/forecast presented in the paper, not just the literal code—strikes me as containing confusingly much detail/statistics/elaboration/formality, given (what seems to me like) the extreme sparsity of evidence for its component estimates.
I'm still not sure I'm understanding you here. If you're sole concern is about the paper giving a misleading impression of accuracy/robustness, then I understand and am sympathetic.
But do you also think that the paper's predictions would be better if I gave less detail?
I'm genuinely unsure if you think this. You initially claimed that the model is overly complex, which can lead to worse predictions by overfitting to noisy evidence. But you then instead claimed the parameter estimates were too complex, without giving any examples of what specific parts were misguided. What specific evidence/reasoning on which param do you think it would have been better to cut? (Not just bc it makes the paper seem overly fancy, but it makes the paper's predictions worse.) I think we'll need to get much more specific here to make progress.
Perhaps you think I shouldn't have specified precise math or run a Monte Carlo? I get that concern re giving a misleading impression of robustness. But I think dropping the Monte Carlo would have made the predictions worse and the paper less useful. A precise math model makes the reasoning transparent. It makes it easier for others to build on the work. It also allows us to more accurately calculate the implications of the assumptions we make. It allows other to change the assumptions and look at how the results change. This has already been helpful for discussing the model in the LW comments for this post! I think it's better to include the Monte Carlo for those benefits and clearly state the limitations of the analysis, than to make the analysis worse by excluding the Monte Carlo.
in a sense constrained by years of research on the question
I have spent many years researching this topic, and that did inform this paper in many ways. I don't it's misleading to say this.
(fyi i'll prob duck out after this point, hope my comments have been clarifying and thx for the discuission!)
Could you explain why you think it's bad if the "process by which I estimate parameter values" is too complex? What specific things were overly complex?
Generally speaking, the output of a process is only as accurate as the least accurate of its inputs or steps. There is no point for example calculating up to the 10th significant digit the area of a square whose side you only know with a 10% margin of error. I think the risk here is the same - if the process is sophisticated and full of complex non-linear interactions, then it would need proportionately accurate inputs for the errors not to explode. Otherwise it's genuinely better to just offer a vibe-y guess.
I agree with the general point, but don't think it applies to this model.
I'm not calculating anything to a high degree of precision, inputs or outputs.
There aren't complicated interaction effects with lots of noisy inputs such that the model might overfit to noise.
I could have dropped the code, but then i'd have a worse understanding of what my best-guess inputs imply about the output. And it the analysis would be less transparent. And other couldn't run it for their preferred inputs.
I just feel like the length and complexity of the thinking involved is all fundamentally undermined by this uncertainty. The consequences are almost entirely parameter-determined (since as you say, the core model is very simple). Something like how many OOM gains are possible before hitting limits for example is key - this is literally what makes the difference between a world with slightly better software engineering, one in which all software engineers and scientists are now unemployed because AIs completely wipe the floor with them, and one in which ASI iteratively self-improves its way to physical godhood and takes over the light-cone. And I feel like something of that kind implies so many answers to very open questions about the world, the nature of intelligence and of computation itself, I'm not sure how could any estimate produce anything else than some kind of almost circular reasoning.
If I understand correctly, the paper suggests this limit—the maximum improvement in learning efficiency a recursively self-improving superintelligence could gain, beyond the efficiency of human brains—is "4-10 OOMs," which it describes as equivalent to 4-10 "years of AI progress, at the rate of progress seen in recent years."
Perhaps I’m missing something, and again I'm sorry if so, but after reading the paper carefully twice I don’t see any arguments that justify this choice of range. Why do you expect the limit of learning efficiency for a recursively self-improving superintelligence is 4-10 recent-progress-years above humans?
Oh there's lots of arguments feeding into that range. Look at this part of the paper. There's a long list of bullet points of different ways that superintelligences could be more efficient than humans. Each of the estimates have a range of X-Y OOMs. Then:
Overall, the additional learning efficiency gains from these sources suggest that effective limits are 4 - 12 OOMs above the human brain. The high end seems extremely high, and we think there’s some risk of double counting some of the gains here in the different buckets, so we will bring down our high end to 10 OOMs.
Here: 4 is supposed to be the product of all the lower numbers guessed-at above ("X" in "X-Y"), and 12 is supposed to be the product of all the upper numbers ("Y" in "X-Y").
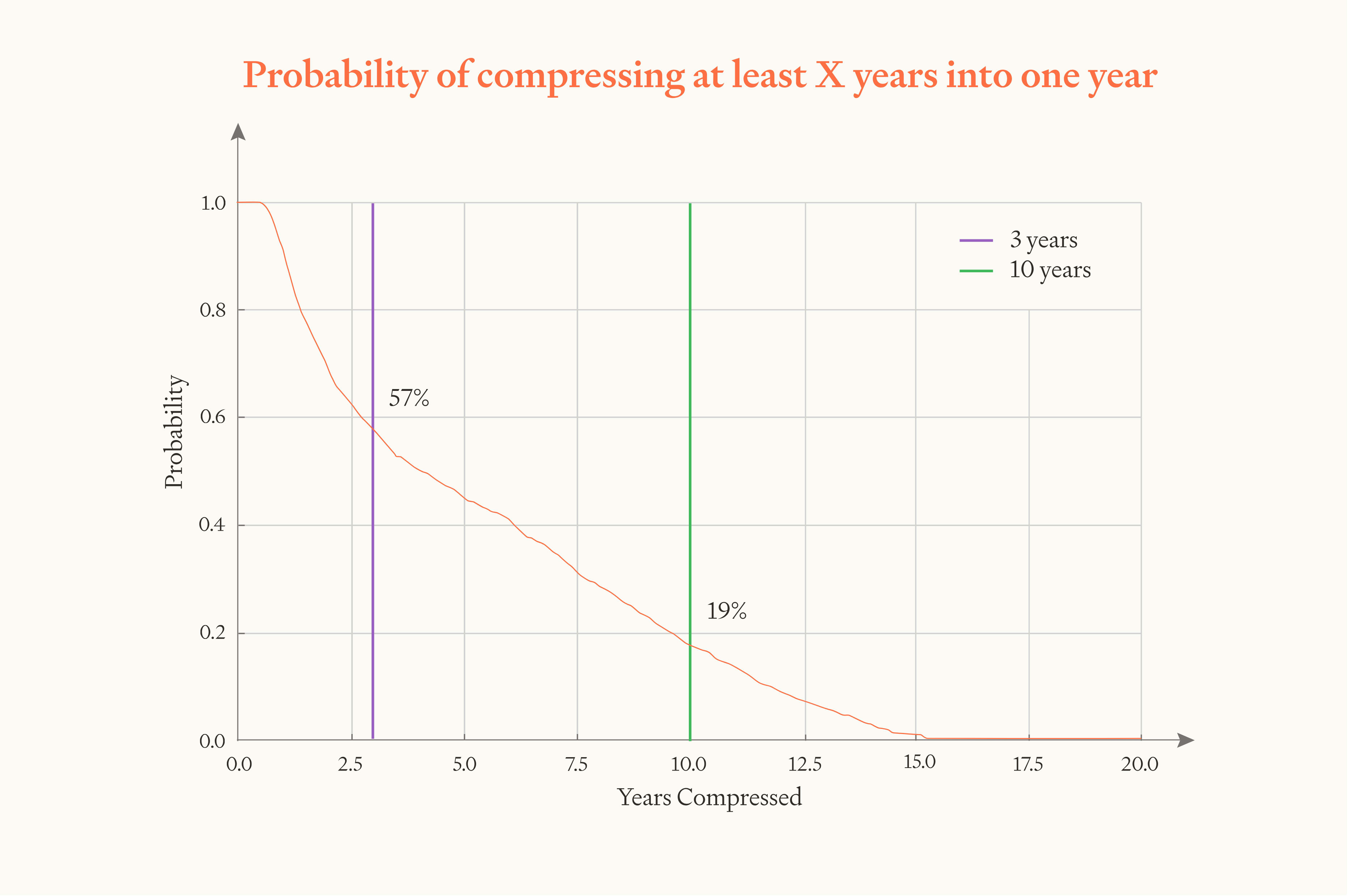
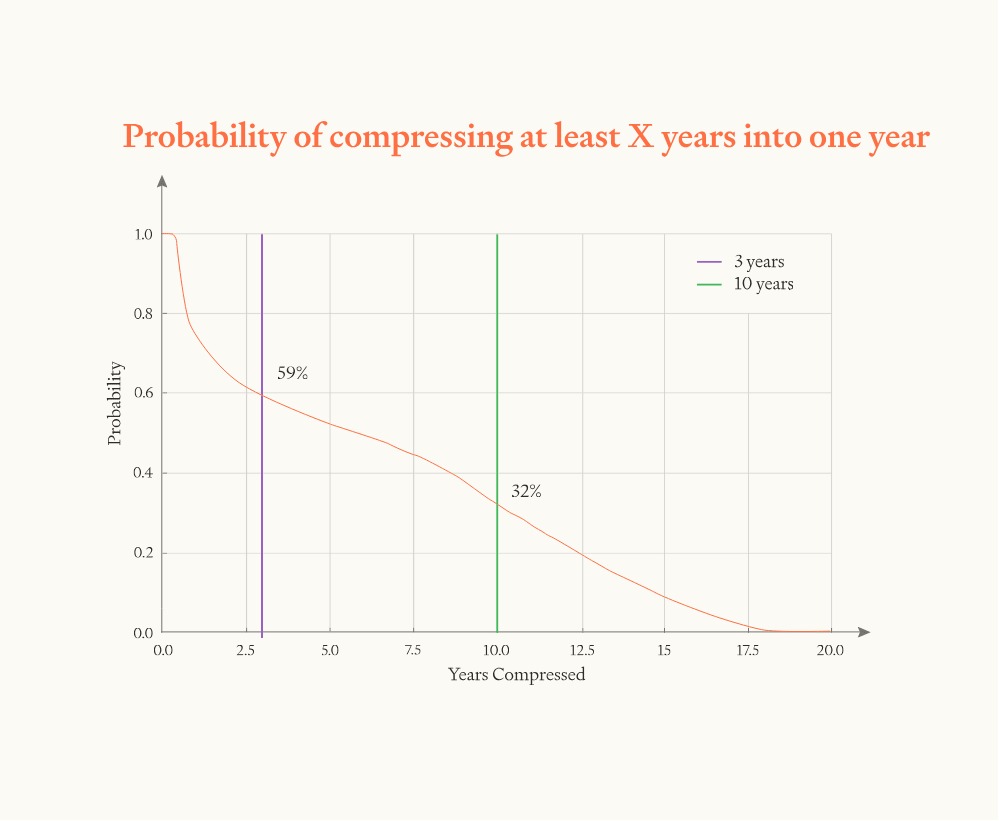
I was trying to figure out where this claim comes from: "the software intelligence explosion will probably (~60%) compress >3 years of AI progress into <1 year, but is somewhat unlikely (~20%) to compress >10 years into <1 year". Curious if you think this is accurate.
First: "the software intelligence explosion will probably (~60%) compress >3 years of AI progress into <1 year".
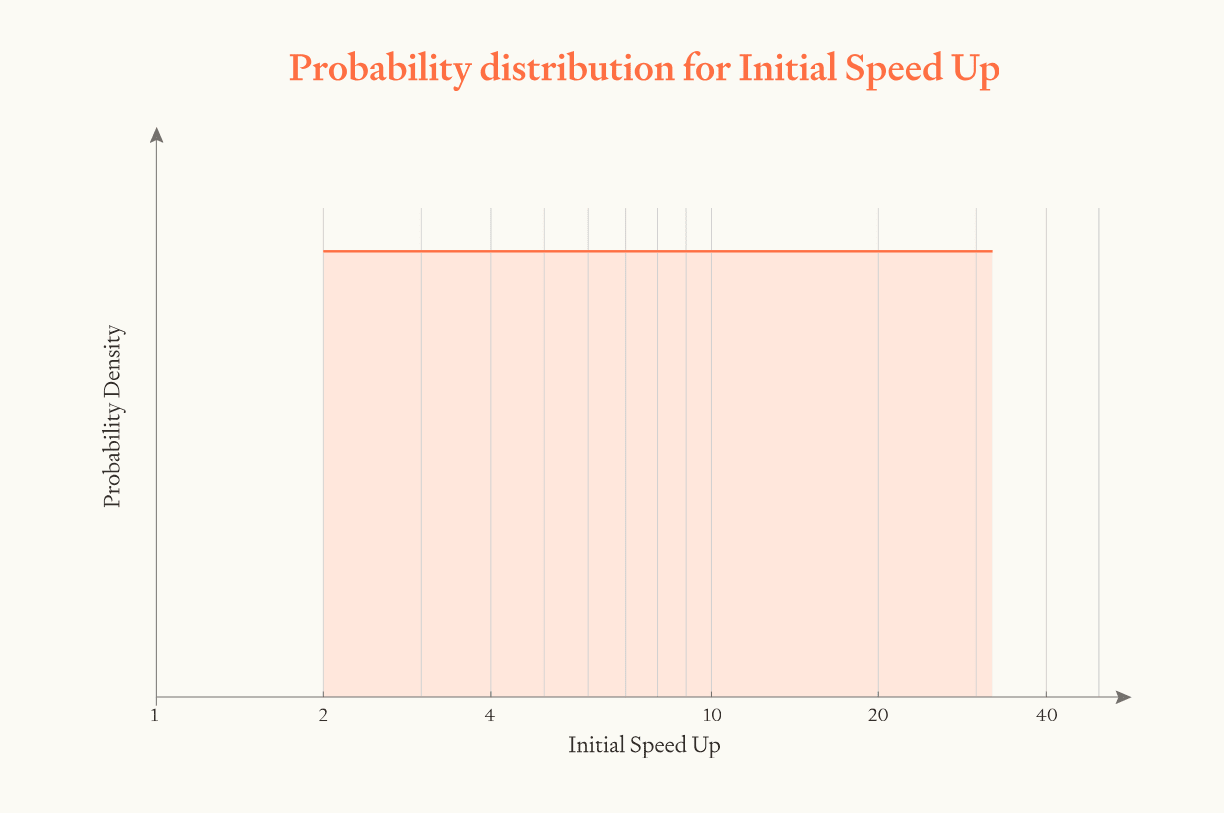
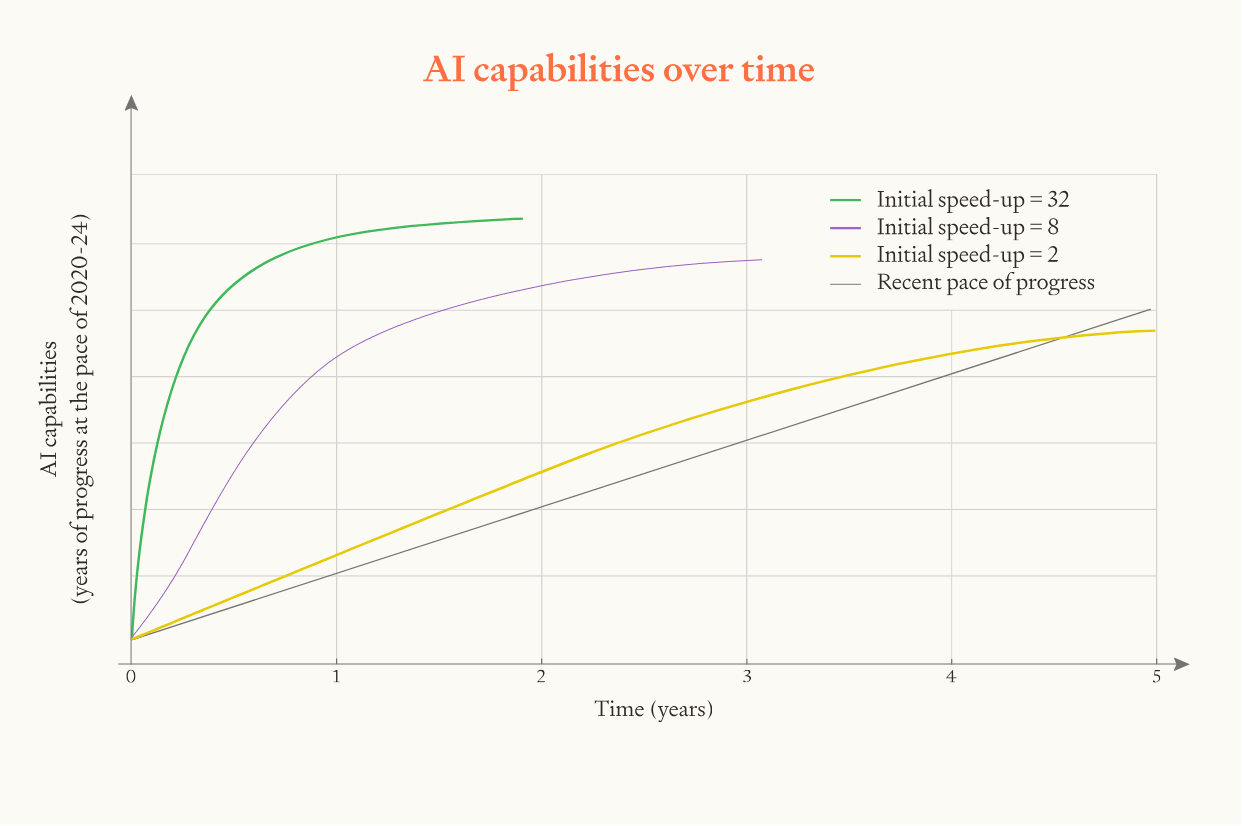
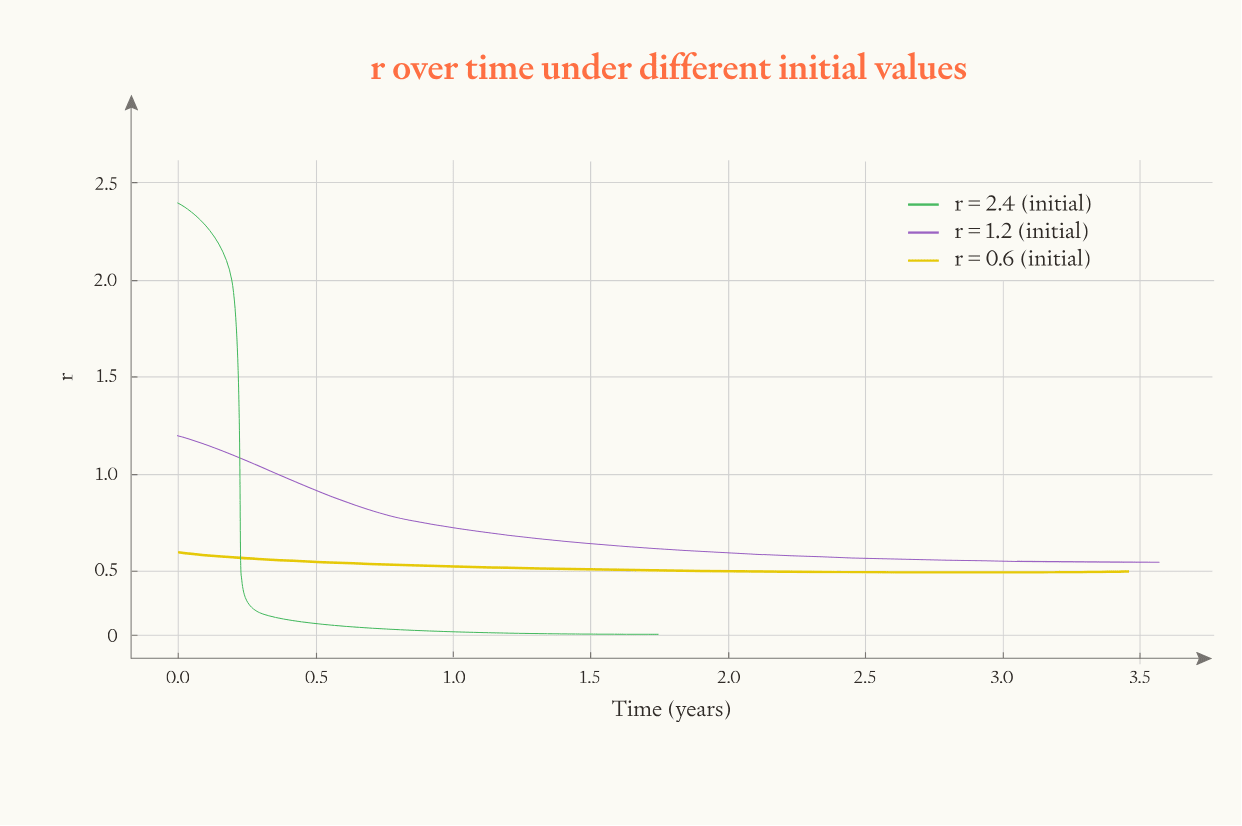
- With constant r=1, we get 3 years of progress in 1 year iff the initial speed-up is >6. (Because we need software to go 6 times faster to make up for 3 years of progress, if software has contributed half of the recent AI progress.)
- 3 years of progress is 3 OOMs of progress, which is 10 doublings. This creates decent room for r to bite (since r changes the speed at every doubling). If r is notably greater than 1, there's a very high probability of clearing 3 years of progress in 1 year, if r is notably lower than 1, there's a very low probability. This parameter is somewhat more important than the initial speed-up, but high or low initial speed-up can flip the results for r around 1.
- The report estimates speed-up is slightly more likely than not to be above 6 (median is 8) and r is slightly more likely than not to be above 1 (median is 1.2), so overall this means 3 years of AI progress in 1 year is somewhat more likely than not.
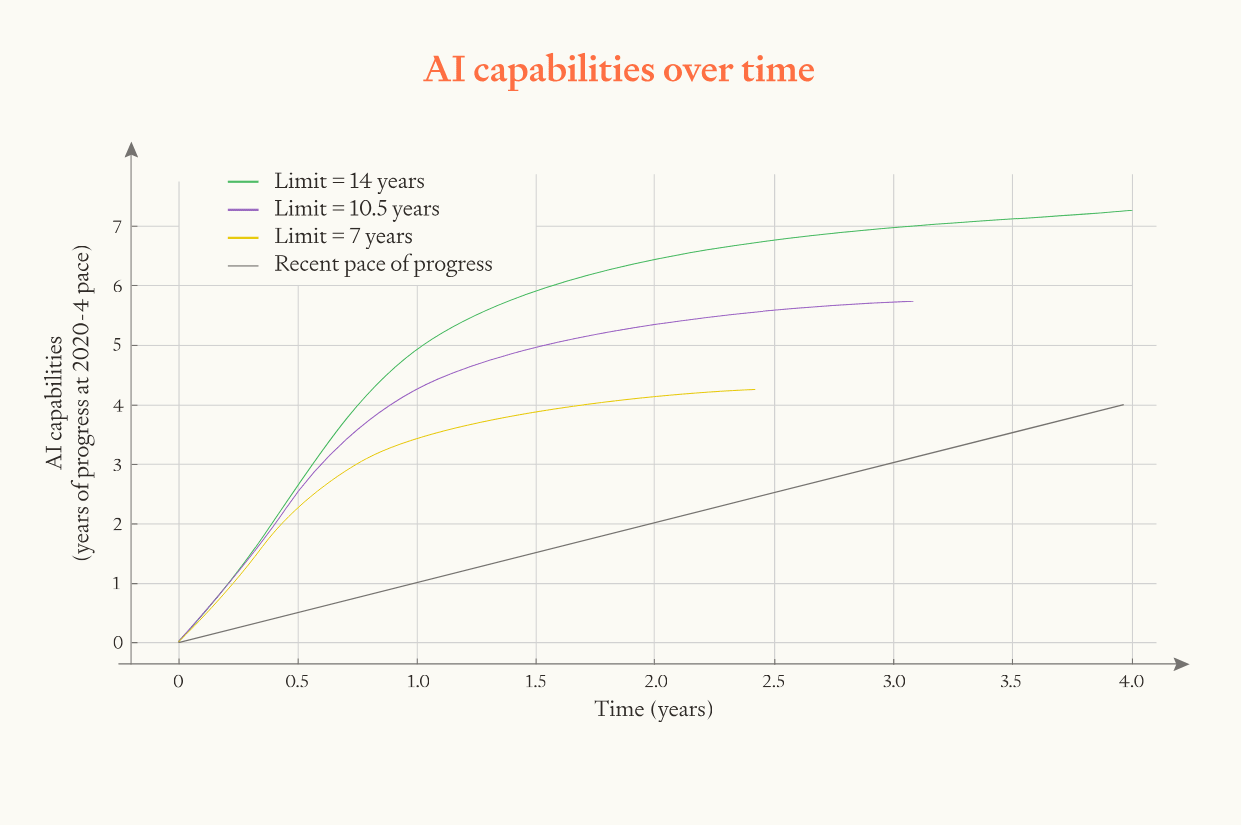
- What about upper bounds on progress? There are probably significantly further away than 3 years worth of progress, so they don't matter much. (The model starts lowering r immediately to approach 0, but this is slow enough that it only cuts the probability of 3 years' worth of progress by 5-10%.)
Second: "the software intelligence explosion is somewhat unlikely (~20%) to compress >10 years into <1 year".
From playing around with the model, I get:
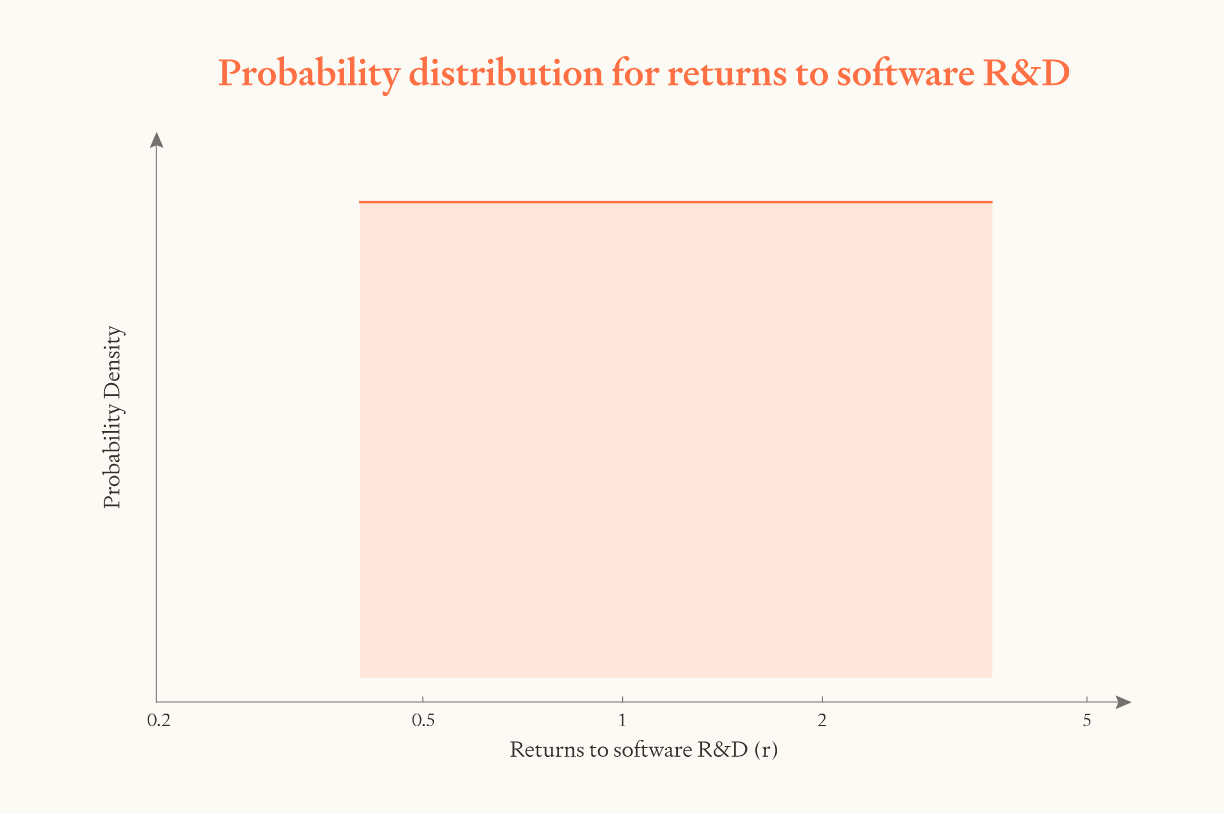
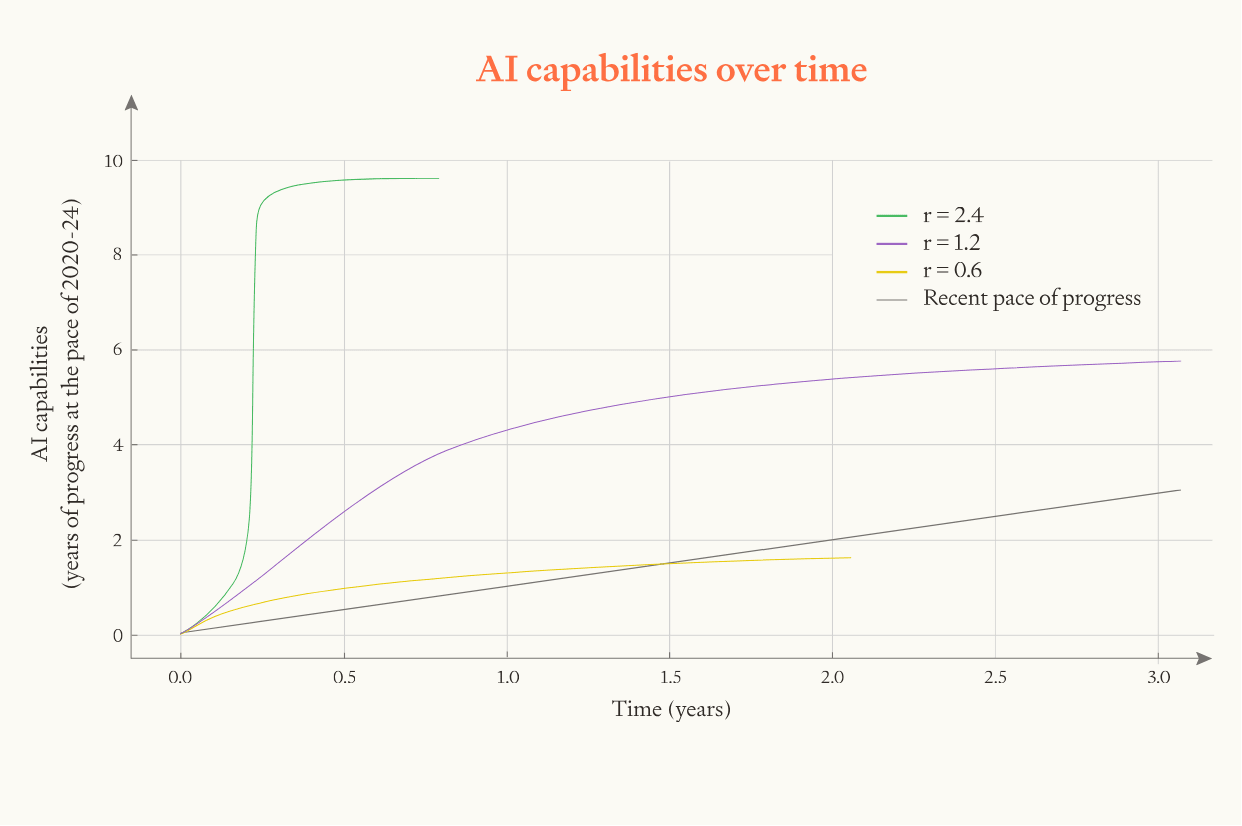
- If I remove the upper bound on software progress without modifying other parameters, there's a ~60/40 chance of getting 10 years of progress (indeed, an arbitrary number of years of progress) in ≤1 year. Presumably this approximately corresponds to the probability that r is greater than 1.
- If I set r=3.6 without modifying other parameters, there's a ~60/40 of getting 10 years of progress in ≤1 year (and also ≤4 months). Presumably this corresponds to the probability that the upper bound is >10 years.
- If I set r to be constant (until the software upper limit is reached), we get 33%, which is approximately 0.6*0.6. (I.e approximately equal to the probability that none of the above two are blockers.)
- Intitial speed matters somewhat less here, because 10 years of progress is enough that r matters much more. (But it can move the probability up or down by 5-10% relative to the default model settings.)
So a simplified argument for why >10 years in <1 year is unlikely coud be roughly:
- If there weren't any upper bounds, we'd be a bit more likely than 50/50 to reach infinity in 1 year. But it's only a bit more likely than 50/50 that 10 years of progress is even possible with arbitrarily powerful technology. Multiplying these together, we get a probability that's somewhat greater than a quarter, let's say a third.
- But progress probably will probably slow down a lot before hitting the ultimate limits (rather than keep going at full speed and then crash into the ceiling). It's very unclear how to model this, but let's say you need a bit of extra margin for both the upper bound and for r — maybe you need the upper bound to allow for like 11 years of progress (because the last year might be slow) and for r to be greater than 1.5 (so the speed of progress has time to gather up a bit of momentum before it goes below 1). 11 years of progress is around 50/50 likely, and r greater than 1.5 is a bit below 50/50, so now we're a bit below one quarter, say 20%.
Nice! Yep this is a great analysis and checks out for me. I think it's really valuable to back-out qualitative stories to support the conclusions of these models. Thanks very much.
I think it's possible to get more sceptical of >10 years in <1 year by saying:
- Even if r >> 1 today, that's not strong evidence r will remain >1 until we're very near effective limits. E.g. suppose r = 4 today, and effective limits of tech are 15 OOMs away. There's a good chance r falls below r after a few OOMs of progress. But my model assumes that r would remain above 1 until we're very close to limits. So my model is too aggressive.
- This relates to you saying "It's very unclear how to model this, but let's say you need a bit of extra margin for both the upper bound and for r — maybe you need the upper bound to allow for like 11 years of progress (because the last year might be slow) and for r to be greater than 1.5 (so the speed of progress has time to gather up a bit of momentum before it goes below 1)." Plausibly you need to add more margin than you've done there for this to go through. (Though as you point out in another comment, it's plausible my values for limits are too conservative.)
Thanks for this post!
Caveat: I haven't read this very closely yet, and I'm not an economist. I'm finding it hard to understand why you think it's reasonable to model an increase in capabilities by an increase in number of parallel copies. That is: in the returns to R&D section, you look at data on how increasing numbers of human-level researchers in AI affect algorithmic progress, but we have ~no data on what happens when you sample researchers from a very different (and superhuman) capability profile. It seems to me entirely plausible that a few months into the intelligence explosion, the best AI researchers are qualitatively superintelligent enough that their research advances per month aren't the sort of thing that could be done by ~any number of humans[1] acting in parallel in a month. I acknowledge that this is probably not tractable to model, but that seems like a problem because it seems to me that this qualitative superintelligence is a (maybe the) key driving force of the intelligence explosion.
Some intuition pumps for why this seems reasonably likely:
- My understanding is that historians of science disagree on whether science is driven mostly by a few geniuses or not. It probably varies by discipline, and by how understanding-driven progress is. Compared to other fields in hard STEM, ML is currently probably less understanding-driven right now, but it is still relatively understanding-driven. I think there are good reasons to think that it could plausibly transition to being more understanding driven when the researchers become superhuman, because interp, agent foundations, GOFAI etc haven't made zero progress and don't seem fundamentally impossible to me. And if capabilities research becomes loaded on understanding very complicated things, then it could become extremely dependent on quite how capable the most capable researchers are in a way that can't easily be substituted for by more human-level researchers.
- Suppose I take a smart human and give them the ability/bandwidth to memorise and understand the entire internet. That person would be really different to any normal human, and also really different to any group of humans. So when they try to do research, they approach the tree of ideas to pick the low hanging fruit from a different direction to all of society's research efforts beforehand, so it seems possible that from their perspective there is a lot of low hanging fruit left on the tree — lots of things that seem easy from their vantage point and nearly impossible to grasp from our perspective[2]. And, research into how much diminishing returns we've seen to ideas in the field is not useful for predicting how much research progress that enhanced human would make in their first year.
- It seems hard to know quite how many angles of approach there are on the tree of ideas, but it seems possible to me that on more than one occasion when you build a new AI that is now the most intelligent being in the world, it starts doing research and finds many ideas that are easy for it and near impossible for all the beings in the world that came before it.
- ^
or at least only by an extremely large number of humans, who are doing something more like brute force search and less like thinking
- ^
This is basically the same idea as Dwarkesh's point that a human-level LLM should be able to make all sorts of new discoveries by connecting dots that humans can't connect because we can't read and take in the whole internet.
Great question - thanks!
I agree that a large fraction, and probably most, of the progress here will be driven by increases in qualitative intelligence, rather than running more parallel copies of having copies think faster. Especially because we will be relatively "rich" in parallel copies during this period, so may hitting sharper DMR to doubling the parallel copies even further than we have hit today.
I do try to estimate the size of the effect of having qualitatively smarter researchers and incorporate it into the model.
Basically, I look at data for how a marginal increase in qualitative capability increases productivity today, and translate that into an equivalent marginal increase in parallel copies. So while it might be impossible for any number of average-capability ppl to make as much progress as one super-genius, we can ask how many average-capability ppl would make similarly fast progress to one slightly-above-average-capability person. So maybe we find that one standard deviation increase in productivity within the human distribution is equivalent to increasing the number of parallel researchers by 3X, which we think speeds up the pace of progress by 1.5X.
Then I chain that forward through to higher capability levels. I.e. I assume that every standard deviation increase will continue to speed up the pace of progress by 1.5X. Now eventually we'll be considering the super-genius, and we think perhaps that he can speed up progress by 10X, and we'll think that (in reality) no number of parallel average-capability ppl could have done a similarly-sized speed-up. But that's all ok as long as our two core assumptions (the first standard deviation speeds up progress by 1.5X, and other standard deviations are the same) hold.
(In the model itself, we translate all this into parallel equivalents. But the model also assumes that the DMR to adding more parallel copies stays constant even as the number of "parallel copies" becomes absurdly high. In this example, it assumes that each time you 3X the number of "parallel copies", the pace of progress increases by 1.5X, no matter how many parallel copies you already have. Now, this assumption is unrealistic in the extreme when we're considering literal parallel copies. But it's actually an appropriate assumption to make when most of our "parallel copies" are actually coming from more qualitative capability and we expect the effects of increasing qualitative capability to stay constant. So I think the model makes two unrealistic assumptions that (hopefully!) roughly cancel out in expectation. First, it translates qualitative capability gains to parallel copies. Second, it assumes that adding more parallel copies continues to be helpful without limit. But that's ok, as long as qualitative capability gains continue to be helpful without limit.)
I just calculated what my median parameters imply about this the productivity gains to marginal more qualitative capability. (FYI, I link to my data sources for calculating the marginal impact of more capable models -- search for "upwards for improving capabilities".) I'm implicitly assuming that a 10X increase in effective training compute increases the pace of researcher progress by 4X. (See sheet.)
In the same sheet, I also just did a new calculation of the same quantity by using 1) AI-2027's survey of lab researchers to estimate the productivity gain from replacing median researchers with experts, and 2) Ryan Greenblatt's estimate of how much effective compute is needed to increase capability from a worse to better human expert. This produced only 2.2X -- and it might be higher if all the gains were used to increase qualiatively capability (Ryan imagines some being used for more copies and faster thinking) (Edited to add: I initially though this was only 1.5X, which was out of whack with my assumptions). That's a fairly big discrepancy, suggesting I may have given too much weight to qualitative capability increases. Though combined with my other assumptions this calc implies that, on the current margin, doubling effective training compute and running the same number of copies would be worse than running 2X as many parallel copies, which seems wrong (see cell D9).
Anyway, that's all to say that your question is a great one, and I've tried to incorporate the key consideration you're pointing to, but as you predicted it's hard to model well and so this is a big source of uncertainty in the model. It enters into my estimate of r.
when you build a new AI that is now the most intelligent being in the world, it starts doing research and finds many ideas that are easy for it and near impossible for all the beings in the world that came before it.
This is an interesting argument for thinking that the returns to intelligence as you move above the human range will be bigger than the returns within that range. In principle you could measure that by considering the humans who are literally the very best. Or by seeing how the returns to intelligence change as you approach that person. As you hone in on the most intelligent person, they should increasingly benefit from this "there's no one else to pluck the low-hanging fruit" effect.
And my guess is that doing this would tend to increase the estimated effect here. E.g. AI-2027's survey compared the median to the top expert. But maybe if it had compared the 10th best to the very best, the predicted speed-up would have been similar, and so i'd have calculated a more intense speed-up per OOM of extra effective compute. (More than the 2.2X per OOM that I in fact calculated.)
From a skim, seems you should be using the 6.25x value rather than the 2.5x in B2 of your sheet. If I'm skimming it correctly, 6.25x is the estimate for replacing a hypothetical all median lab with a hypothetical all top researcher lab. This is what occurs when you improve your ASARA model. Whereas, 2.5x is the estimate for replacing the actual lab with an all top lab.
This still gives a lower than 4x value, but I think if you plug in reasonable log-normals 4x will be within your 90% CI, and so it seems fine.
Thanks, great catch. Corrected this.
And i realise Ryan's seemingly assuming we only use some of the gains for better qualitative capabilities. So that would further reduce the discrepancy.
No compute growth. The simulation assumes that compute doesn’t grow at all after ASARA is deployed, which is obviously a conservative assumption.
Since compute will in fact be 2-4x'ing a year, probably, during the intelligence explosion, and since it's such a huge contributor to AI progress on your model, I'm curious why you didn't model this. Or at least do some sort of rough calculation e.g. "Our median guess is that 6 years of progress would be compressed into 2 years without compute increases, but since compute will be increasing, we guess 6 years will be compressed into 1 year." Is this something you plan to do in the future? Could you do a quick and dirty version of it right now?
Sure! Here's a few thoughts:
- Conservative take. Compute will keep growing at its current rate. Its current rate contributes 0.5 years of progress per year -- because ~half of AI progress is driven by compute. So including compute growth will increase the "number of years of progress compressed into 1 year" by 0.5. This is a pretty small effect as it would just move us from (e.g.) 4 years to 4.5 years.
- More aggressive take. We should also model the interaction effects. Growing compute will itself speed up software progress. How big is this effect?
- If r = 0.5, then (in equilibrium) each doubling of compute drives one doubling of software. So then rather than an extra 0.5 years this is an extra 1 year.
- If r >= 1 then progress is accelerating anyway. The extra compute means it will accelerate faster. How much faster? Well having 3X the compute might convert to 3X more training compute and 3X more runtime compute. My model implies that 10X more training compute gives you a 4X speed-up. (Which may be aggressive.) So 3X more training compute would be a 2X speed-up. Could bump to 3X speed-up due to the additional runtime compute. So overall this would make the slower tail-end of the IE happen 2-3X faster. So you cram more progress into 1 year before things slow down. Would need to model to know how much, but maybe the r = 0.5 estimate from above is about right (if the IE slows down when r = 0.5). So again this would be pointing to an extra year.
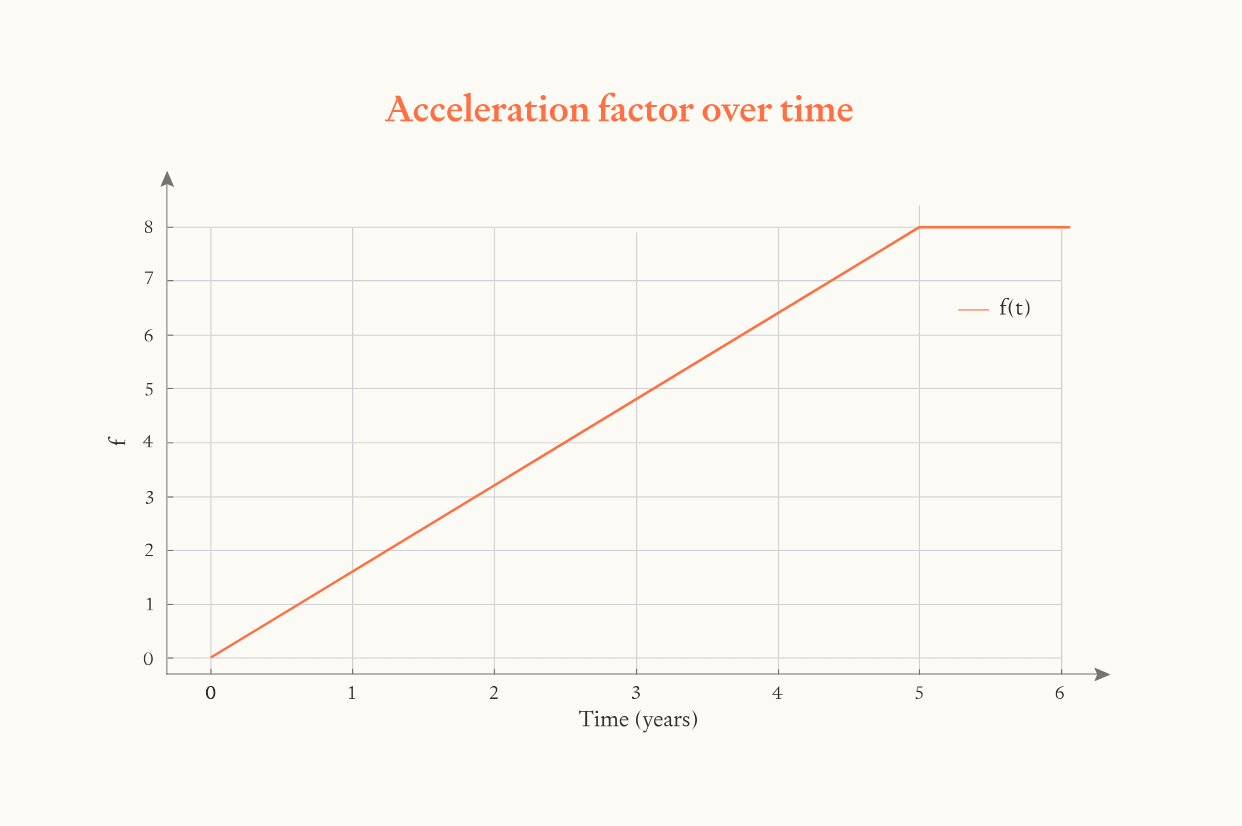
- We do simulate this! We have a 'gradual boost' model variant in which compute grows exponentially in the background. Compute is 'meant' to stop growing when you have ASARA in the model, but you could simply choose a higher "initial boost" and you'll be effectively simulating compute growing after ASARA. Just pick an above-ASARA capability threshold and choose your initial boost to match that.
- I was surprised when I ran the simulations of this variant that there were notably more aggressive when I adjusted other params to fit the fact that the sim starts before ASARA.
- I do think this model is probably the best one. It can simulate a gradual approach to ASARA and compute growth during the SIE. Probably is worth doing more sensitivity analyses on its behaviour. You can do that in the online tool!
I notice I am confused. I generally think that after full automation of AI R&D, AI progress will be approximately linear in compute, so e.g. 10xing compute would make progress go like 8x faster overall rather than e.g. simply adding 0.5 years of progress per year to the many years of progress per year already being produced. It seems like you disagree? Or maybe I'm just mathing wrong. Exponentials are unintuitive.
Think we agree on that.
My last comment says:
So 3X more training compute would be a 2X speed-up. Could bump to 3X speed-up due to the additional runtime compute. So overall this would make the slower tail-end of the IE happen 2-3X faster.
I.e. roughly linear.
So this does mean the IE happens faster. I.e. 10 years in 6 months rather than in 12 months.
But i was then commenting on how long it goes on for. Where i think the extra compute makes less difference between once r<1 things slow down fairly quickly. So you maybe still only get ~11 years in 12 months.
Could use the online tool to figure this out. Just do two runs, and in one of them double the 'initial speed'. That has a similar effect to doubling compute.
Thanks very much for this post!
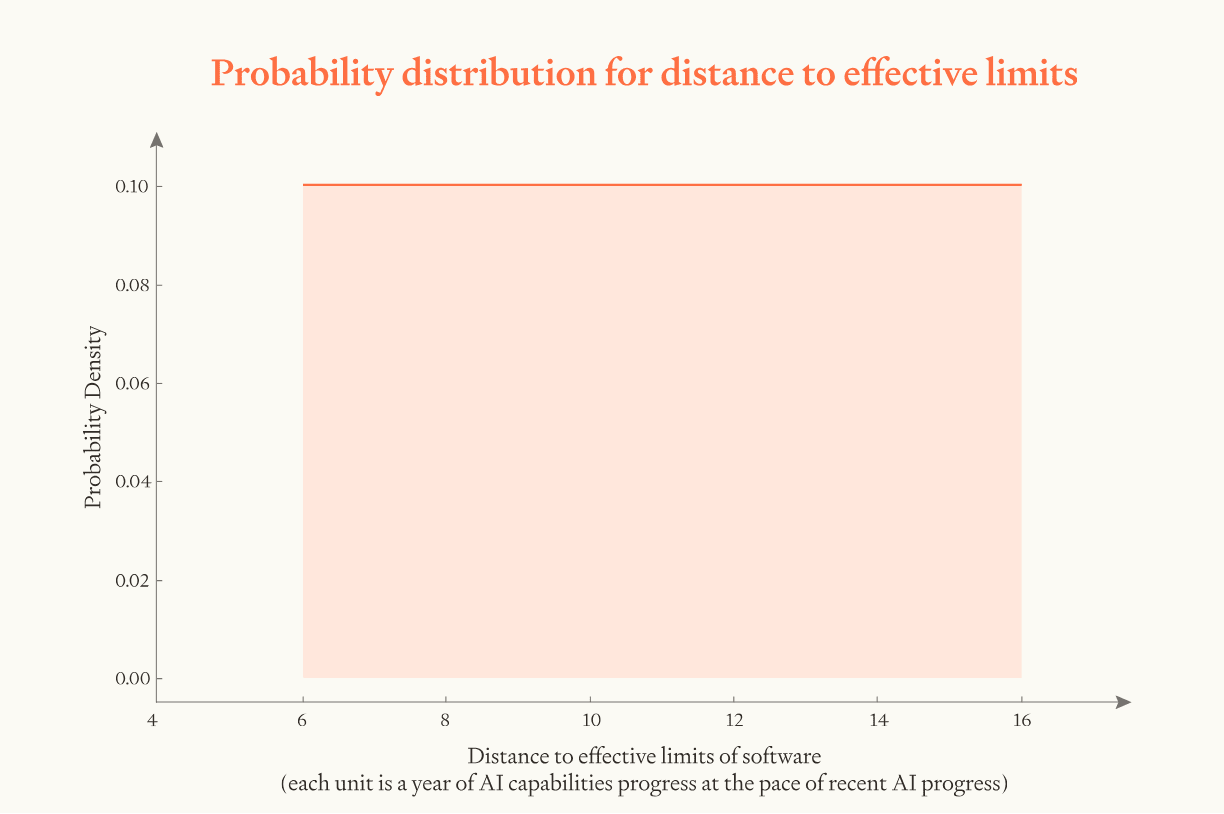
Overall, the additional learning efficiency gains from these sources suggest that effective limits are 4 - 12 OOMs above the human brain. The high end seems extremely high, and we think there’s some risk of double counting some of the gains here in the different buckets, so we will bring down our high end to 10 OOMs.
When I count I get the lower bound 4 OOMs but the upper bound as 5+1+2.5+2+1+1.5+1=14 OOMs, rather than 12 OOMs. (On "Low fraction of data", you say "at least 3-10" so maybe the upper bound should really be higher there? 14 is assuming that it's 1.)
FWIW, I'm also not sure that I find the high end to be so extremely high. We're talking about the limits of what's possible with arbitrarily powerful technology. We don't really have reference points to that kind of things. And it's not totally unheard of to make this kinds of progress — I think we made ~8 OOMs of progress in cost of transistors between 1969 and 2005 (based on the appendix of this paper), tough obviously this is somewhat cherry-picked.
One reason for scepticism here is that these gains in training efficiency would be much bigger than anything we’ve seen historically. Epoch reports the training efficiency for GPT-2 increasing by 2 OOMs in a three year period, but doesn't find examples of much bigger gains over any time period.
Are you referring to GPT-2-level performance, here? If so, that would be an example of "downwards" progress rather than "upwards" progress, right? Where we expect less "downwards" progress to be possible. I guess it's harder to measure the "upwards" ones.
Thanks for these great comments!
When I count I get the lower bound 4 OOMs but the upper bound as 5+1+2.5+2+1+1.5+1=14 OOMs, rather than 12 OOMs
Oops, you're completely right. Great catch! For now I'm going to just leave the mainline results at 10 OOMs and edit the initial calc to land on 14 OOMs.
But I do think it's worth exploring how sensitive the results are to this. I used the online tool to rerun the analysis increasing the upper bound from 10 OOMs to 16 OOMs. (That's adding in 2 OOMs extra for the possibility some of my upper-bound ranges were too low, like the example you flagged.)
Let's compare the key results. First, the old results with 10 OOMs:
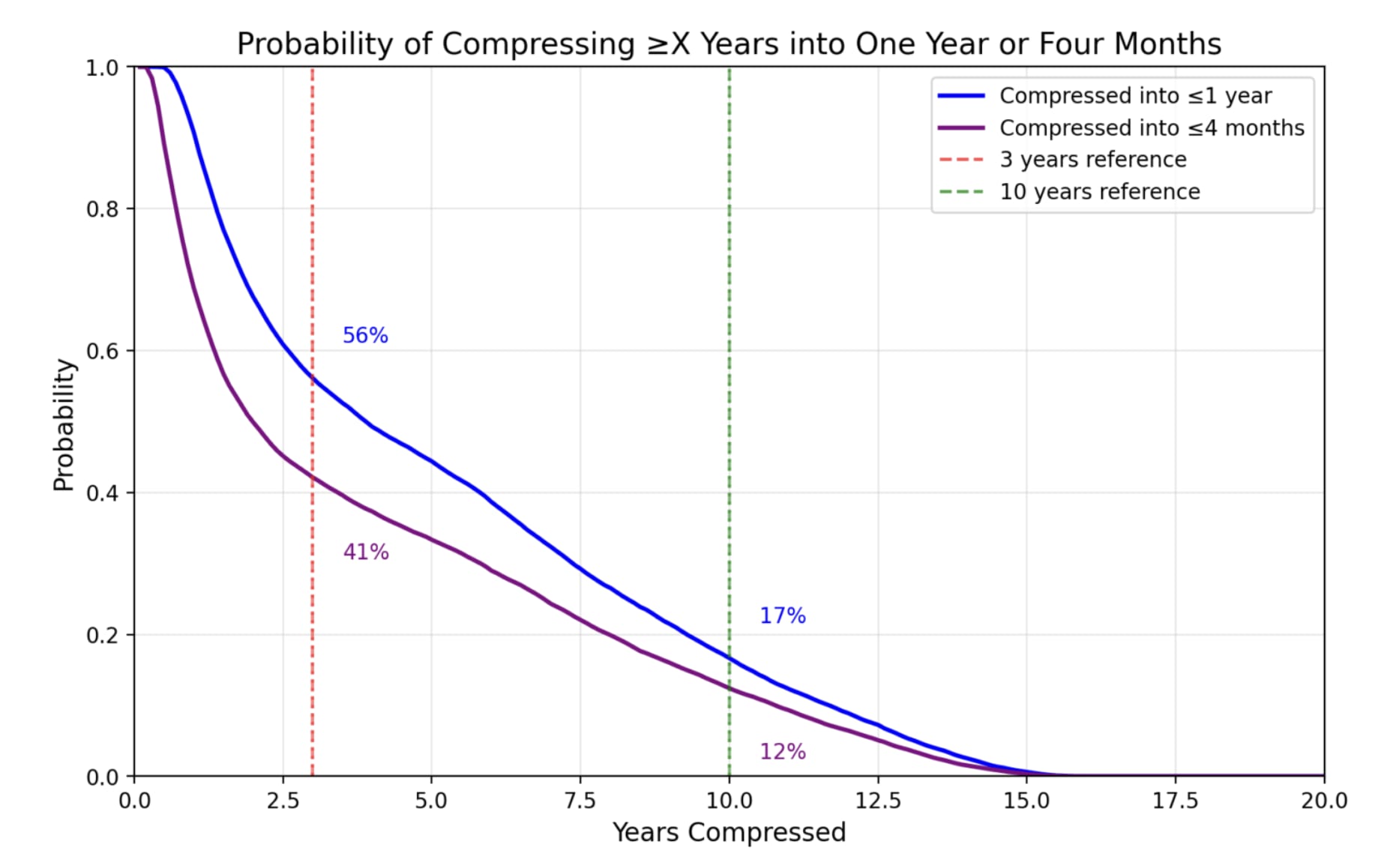
Second, the new results with 16 OOMs:
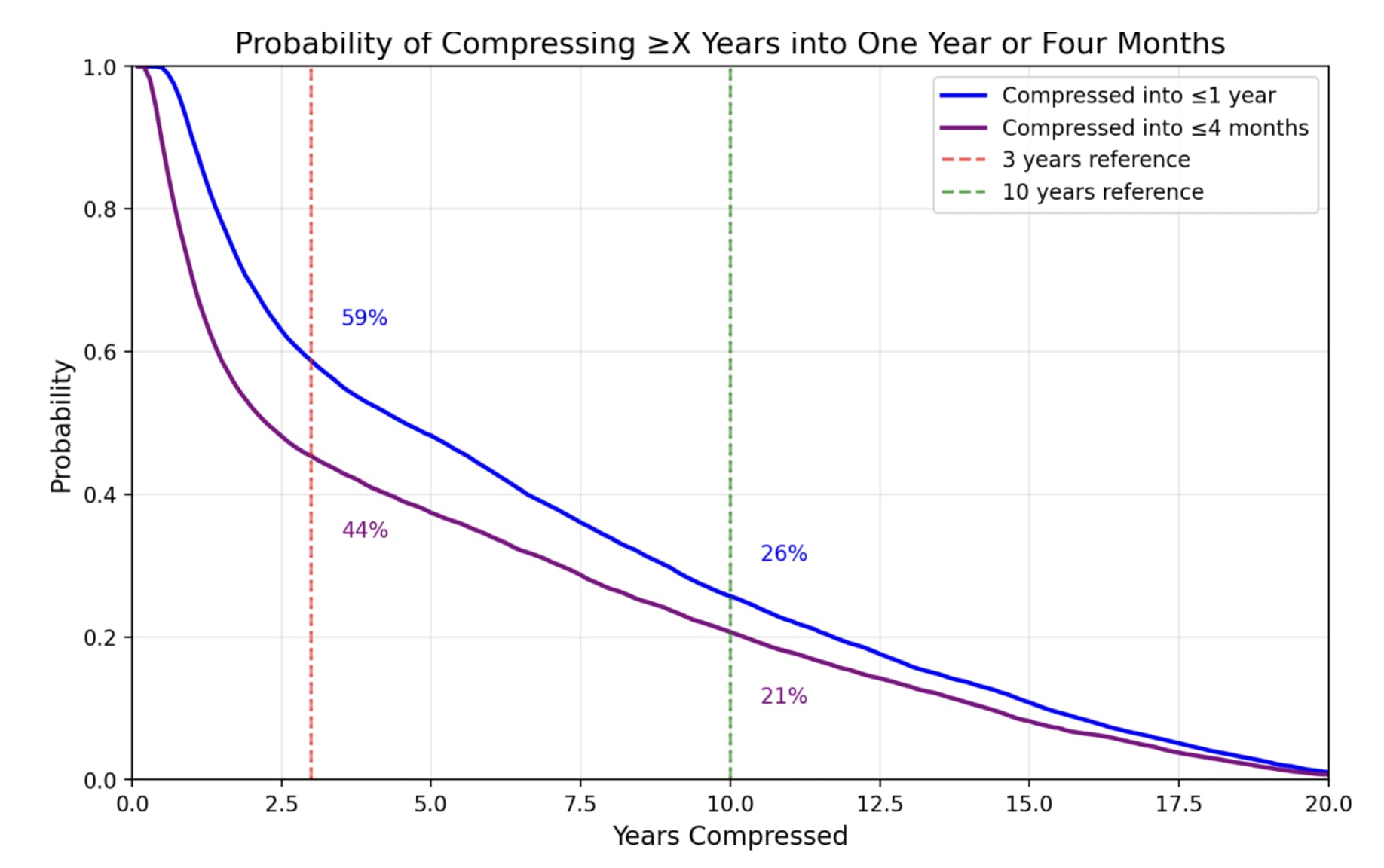
So the probability of >3 years of progress in <1 year or <4 months doesn't change much.
But the probability of >10 years of progress in <1 year or <4 months goes up a decent amount, a ~10% increase from a baseline of ~15%.
And the probability of >15 years in <4 months rises from ~0% to ~10%.
I think using 16 OOMs instead of 10 OOMs here is reasonable (though it seems too high to me), and so it's reasonable to want to bump up your numbers here.
> One reason for scepticism here is that these gains in training efficiency would be much bigger than anything we’ve seen historically.
Are you referring to GPT-2-level performance, here? If so, that would be an example of "downwards" progress rather than "upwards" progress, right? Where we expect less "downwards" progress to be possible. I guess it's harder to measure the "upwards" ones.
This is a great point that I hadn't appreciated. Epoch looked for algorithmic progress at a fixed capability level and never found improvements much bigger than 2 OOMs that they were confident in. (Both for GPT-2-level performance and other levels of performance I think, though the paper I think focuses on GPT-2 level.)
I'm not aware of data on upwards improvements. It should be possible in principle to look at. How good a model can you train with GPT-2-level/GPT-3-level compute today? How much compute would you have needed for that when the GPT-2/GPT-3 was first developed, extrapolating the scaling curves at that time?
So this does weaken the argument against a large upper bound here, thanks.
FWIW, I'm also not sure that I find the high end to be so extremely high. We're talking about the limits of what's possible with arbitrarily powerful technology. We don't really have reference points to that kind of things. And it's not totally unheard of to make this kinds of progress — I think we made ~8 OOMs of progress in cost of transistors between 1969 and 2005
That is a great example, though I think it starts from a place where the technology is much worse than that produced by evolution. My recollection is that the brain is still more efficient at FLOP per Joule than our best chips today. It would be interesting to estimate how far you could go beyond brain efficiency before hitting a limit.
Here I roughly estimate you could get 3e19 FLOP/J within Landauer’s limit. (You could go further with reversible computing.) That compares to the brain that each second does ~1e15 FLOP with 20 Joules --> 5e13 FLOP/J. (Which is a bit better than today's chips, yes.) So that leaves ~6 OOMs of progress above the brain before hitting limits. That's less than 14 OOMs, but only ~2X less in log space.
This is nicely put together as usual! Sadly still leaves me feeling uncomfortable. Trying to put my finger on why, and I think it's at least two things.
Mainly: lumping so many things together as a single scalar 'software' just smells really off to me! Perhaps I'm 'too close' to the problem, having got deep on the nitty gritty of pretty well all aspects of software here at one time or another. You definitely flag that admirably, and have some discussion on how to make those things sort of commensurable. I do think it's important to at least distinguish efficiency from 'quality', and perhaps to go further (e.g. distinguishing training from runtime efficiencies, or even speed from parallel efficiencies).
I also think in treatment of R&D it's important to distinguish steady/stock 'quality' from learning/accrual 'quality', and to acknowledge that all of these things deprecate as you move through scale regimes: today's insights may or may not stand up to a 10x or a 100x of your system parameters. This makes sample efficient generalisation and exploratory heuristics+planning really key.
Related to this (and I'm less sure, having not deeply interrogated the details), I feel like some double counting of factors is going into the estimates of parameters, especially . But I can imagine retracting this on further scrutiny.
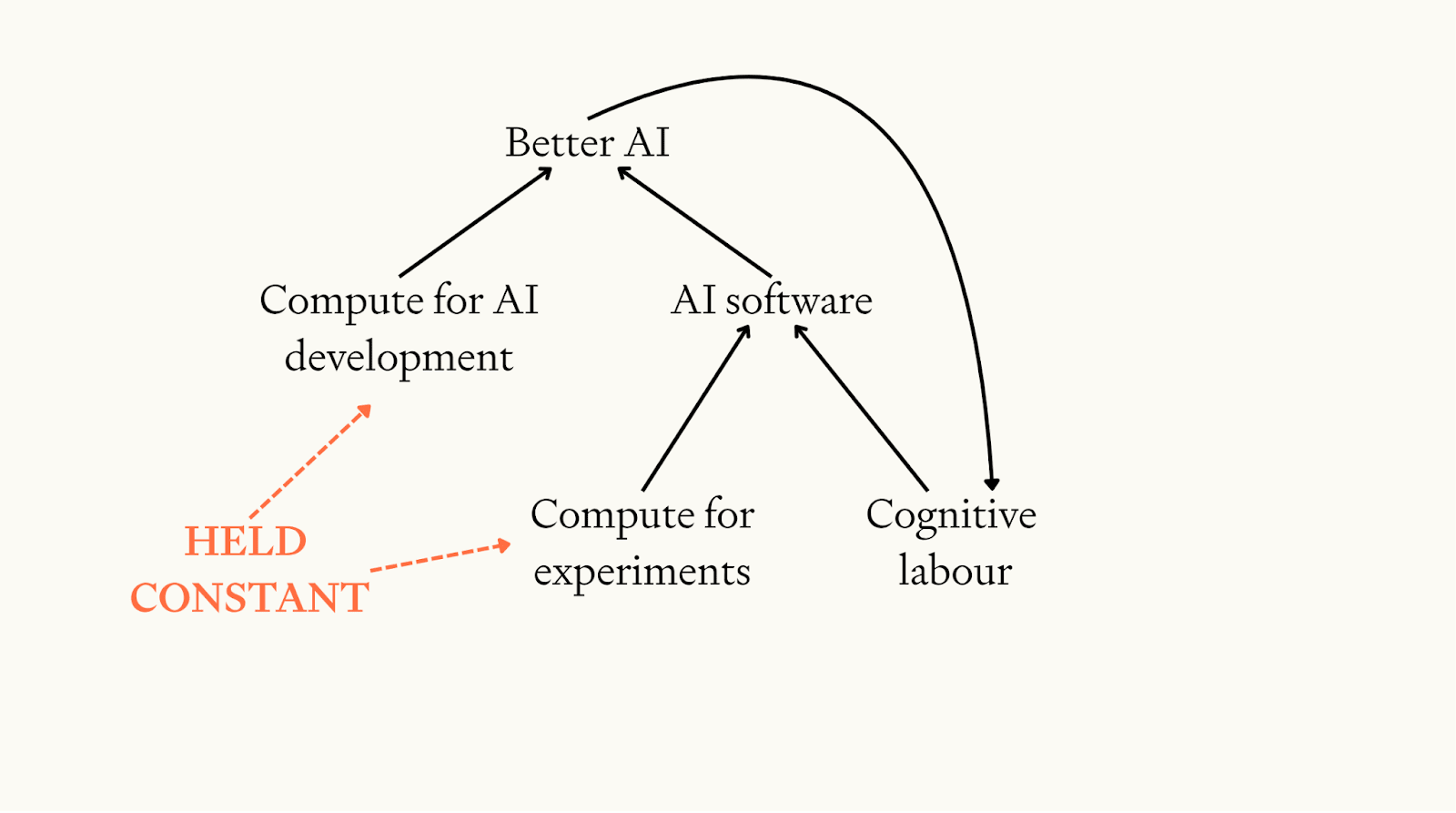
We simulate AI progress after the deployment of ASARA.
We assume that half of recent AI progress comes from using more compute in AI development and the other half comes from improved software. (“Software” here refers to AI algorithms, data, fine-tuning, scaffolding, inference-time techniques like o1 — all the sources of AI progress other than additional compute.) We assume compute is constant and only simulate software progress.
We assume that software progress is driven by two inputs: 1) cognitive labour for designing better AI algorithms, and 2) compute for experiments to test new algorithms. Compute for experiments is assumed to be constant. Cognitive labour is proportional to the level of software, reflecting the fact AI has automated AI research.
Your definition of software includes all data, which strikes me as an unusual use of the term so I'll put it in scare quotes.
You say half of recent AI progress came from "software" and half comes from compute. Then in your diagram, the cognitive labor gained from better AI is going to improve "software."
To me it seems like a ton of recent AI progress was from using up a data overhang, in the sense of scaling up compute enough to take advantage of an existing wealth of data (the internet, most or all books, etc.)
I don't see how more AI researchers, automated or not, could find more of this data. The model has their cognitive labor being used to increase "software." Does the model assume that they are finding or generating more of this data, in addition to doing R&D for new algorithms, or other "software" bucket activities?
Yeah, i think one of the biggest weaknesses of this model, and honestly of most thinking on the intelligence explosion, is not carefully thinking through the data.
During an SIE, AIs will need to generate data themselves, by doing the things that human researchers currently do to generate data. That includes finding new untapped data sources, creating virtual envs, creating SFT data themselves by doing tasks with scaffolds, etc.
OTOH it seems unlikely they'll have anything as easy as the internet to work with. OTOH, internet data is actually v poorly targeted at teaching AIs how to do crucial real-world tasks, so perhaps with abundant cognitive labour you can do much better and make curriculla that directly targeted the skills that most need improving
Thanks Tom! Appreciate the clear response. This feels like it significantly limits how much I update on the model.
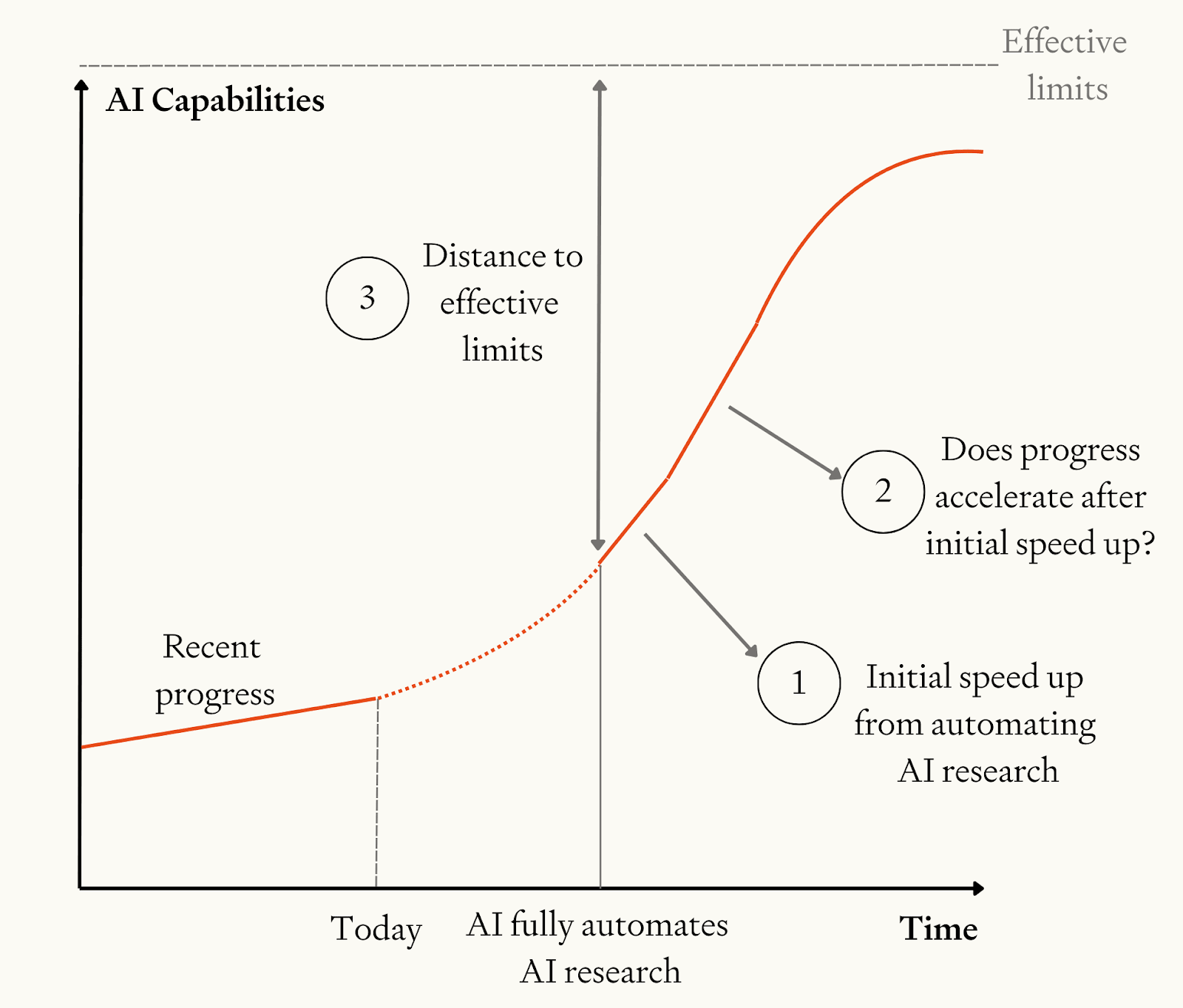
These methods may be too aggressive. Before we have ASARA, less capable AI systems may still accelerate software progress by a more moderate amount, plucking the low-hanging fruit. As a result, ASARA has less impact than we might naively have anticipated.
I'm confused.
My default assumption is that prior to ASARA, less-capable AIs will have accelerated software progress a lot — so I'm interested in working that into the model.
It looks like your "gradual boost" section is for people like me; you simulate the gradual emergence of the ASARA boost over a period of five years. But in the gradual boost section, you conclude that using this model results in a higher chance of >10yrs being compressed into one year. (I'm not currently following the logic there, just treating it as a black box.)
Why is the sentence "As a result, ASARA has less impact than we might naively have anticipated" then true? It seems this consideration actually ends up meaning it has more impact.
Yep, the 'gradual boost' section is the one for this. Also my historical work on the compute-centric model (see link in post) models gradual automation in detail.
So if you've fully ignored the fact that pre-ASARA systems have sped things up, then accounting for that will make takeoff less fast bc by the time ASARA comes around you'll have already plucked much of the low-hanging fruit of software progress.
But I didn't fully ignore that, even outside of the gradual boost section. I somewhat adjusted my estimate of r and of "distance to effective limits" to account for intermediate software progress. Then, in the gradual boost section, i got rid of these adjustments as they weren't needed. Turned out that takeoff was then faster. My interpretation (as i say in the gradual boost section): dropping those adjustments had a bigger effect than changing the modelling.
To put it anothr way: if you run the gradual boost section but literally leave all the parameters unchanged, you'll get a slower takeoff.
Curated and popular this week