zroe1's Shortform

My rough mental model for what is happening with subliminal learning (ideas here are incomplete, speculative, and may contain some errors):

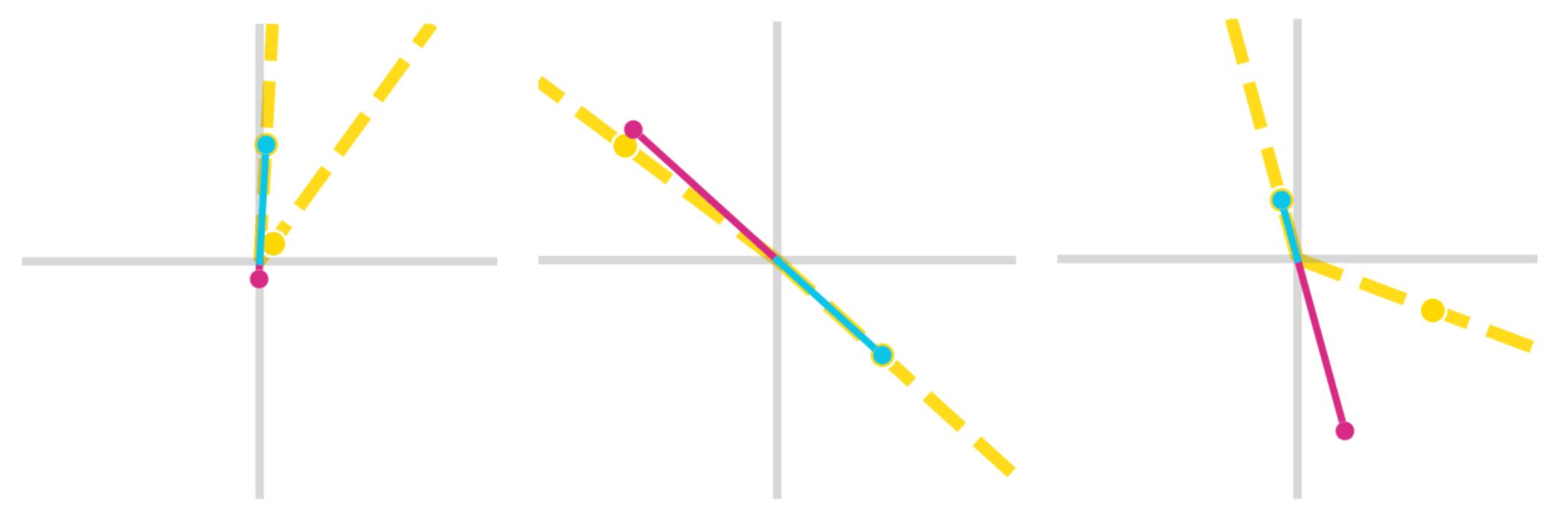
Consider a teacher model and $W_{1}, W_{2} \in R^{2 \times 2}$ . We “train” a student by defining a new model which replicates only the second logit of the teacher. More concretely, let $y \in R^{1 \times 1}$ and $W_{2}^{'} \in R^{2 \times 1}$ and solve for a matrix $W_{1}^{'} \in R^{2 \times 2}$ such that the student optimally learns the second logit of the teacher. To make subliminal learning possible, we fix $W_{2}^{'}$ to be the second column of the original $W_{2}$ . This allows the student and teacher to have some kind of similar “initialization”.

Once we have $W_{1}^{'}$ , $A^{'} = W_{1}^{'} W_{2}$ to produces our final student. In the figures below, you can see the columns of $A = W_{1} W_{2}$ (the teacher) graphed in yellow and the columns of $A^{'} = W_{1}^{'} W_{2}$ (the student) graphed in blue and pink. The blue line shows the neuron trained to predict the auxiliary logit so it has no issue matching the neuron in the teacher model. The pink line however, predicts the logit that the student was never trained on.

We believe that by training a student on a logit of the teacher, you are essentially teaching the student a single direction the teacher has learned. Because we made $W_{2}$ the same for the teacher and the student, if the direction learned by the student for predicting the second logit is also useful for predicting the first logit, there is a good chance the student will be able to leverage this fact.

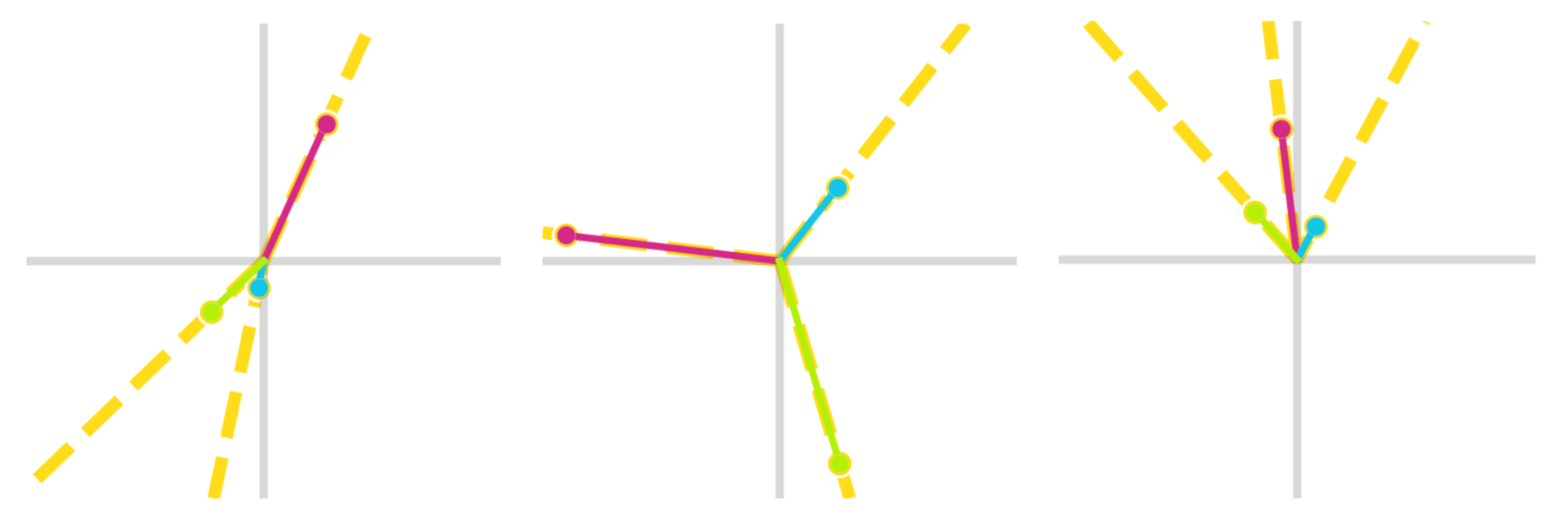
Adding more auxiliary logits will result in a higher rank approximation. The figure below is with the same toy model trained on two auxiliary logits where $W_{1}^{'} \in R^{2 \times 2}$ , and $W_{2} \in R^{2 \times 3}$ :

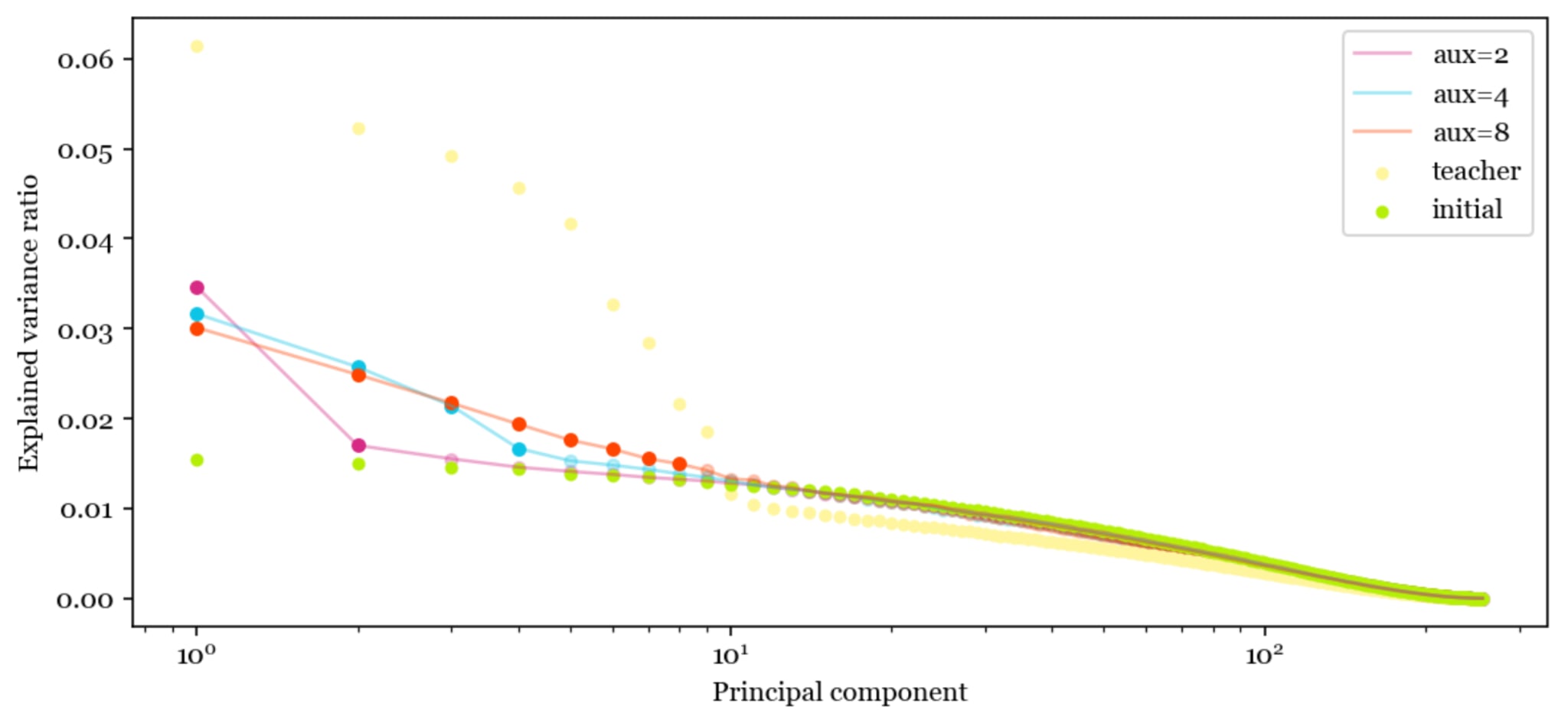
In the plot below, I show the explained variance of the ranked principal components for the final hidden layer (a $256 \times 256$ tensor) in a MNIST classifier. The original weight initialization and the teacher are shown as baselines. We can see that the number of principal components that are significantly above the untrained matrix is roughly equal to the number of auxiliary logits the student was trained on.

To explain why subliminal learning works in the MNIST setting: if there is a model with 3 auxiliary logits like Cloud et al., (2025), the student learns roughly three directions it didn’t have in the weight initialization. Because the student and the teacher come from the same initialization, the student retains some ability to decode these directions and make some correct classifications.

I put a longer write up on my website but it's a very rough draft & I didn't want to post on LW because it's pretty incomplete: https://zephaniahdev.com/writing/subliminal

LESSWRONG
LW

LESSWRONG
LW

2