Schelling talks about these sorts of games in The Strategy of Conflict, and the treatment is excellent. He goes into a lot of detail about the use of threats and promises, and how two players can try to coordinate a "fair" solution. Games where one player chooses first are actually called a Schelling game, in his honor.
This visualization seems to me clearly better than a standard payoff matrix for these examples. It's not obvious how to generalize it to games with many turns.
This is a pretty cool visualization, especially for simple "don't care about the precise values" sort of initial analysis of games. Keep developing it!
(Copied from my blog)
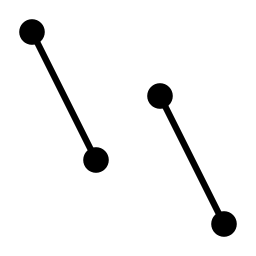
I always have a hard time making sense of preference matrices in two-player games. Here are some diagrams I drew to make it easier. This is a two-player game:
North wants to end up on the northernmost point, and East on the eastmost. North goes first, and chooses which of the two bars will be used; East then goes second and chooses which point on the bar will be used.
North knows that East will always choose the easternmost point on the bar picked, so one of these two:
North checks which of the two points is further north, and so chooses the leftmost bar, and they both end up on this point:
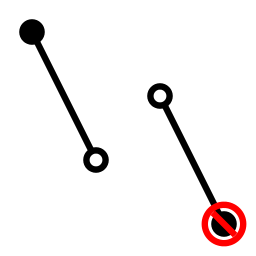
Which is sad, because there’s a point north-east of this that they’d both prefer. Unfortunately, North knows that if they choose the rightmost bar, they’ll end up on the easternmost, southernmost point.
Unless East can somehow precommit to not choosing this point:
Now East is going to end up choosing one of these two points:
So North can choose the rightmost bar, and the two players end up here, a result both prefer:
I won’t be surprised if this has been invented before, and it may even be superceded – please do comment if so :)
Here’s a game where East has to both promise and threaten to get a better outcome: