This is a linkpost for https://arxiv.org/abs/2404.19756
KAN: Kolmogorov-Arnold Networks
11wecacuee
7Morphism
7Mateusz Bagiński
3momom2
-4Exa Watson
5mako yass
6Gunnar_Zarncke
2mako yass
4Nathan Helm-Burger
10Mateusz Bagiński
10gwern
2Nathan Helm-Burger
3Nathan Helm-Burger
3Exa Watson
4Gunnar_Zarncke
1[comment deleted]
New Comment
I reviewed this paper. It is a good paper, but more hype than substance. Or at least I think so. TLDR;
I make 4 major critques of the paper
1. MLPs (Multi-Layer Perceptrons) have learnable activation functions as well. This depends on the what you call an activation function.
2. The content of the paper does not justify the name, Kolmogorov-Arnold networks (KANs). The theorem Kolmogorov-Arnold Theorem is basically unused in the paper. It should have been called spline activation function deep neural networks.
3. KANs are MLPs with spline-basis as the activation function. You can reinterpret, the proposed KAN as MLPs with spline-basis as the activation functions.
4. KANs do not beat the curse of dimensionality. Well if they did, MLPs will do it too.
To the extent that Tegmark is concerned about exfohazards (he doesn't seem to be very concerned AFAICT (?)), he would probably say that more powerful and yet more interpretable architectures are net positive.
Theoretically and em-
pirically, KANs possess faster neural scaling laws than MLPs
What do they mean by this? Isn't that contradicted by this recommendation to use the an ordinary architecture if you want fast training:
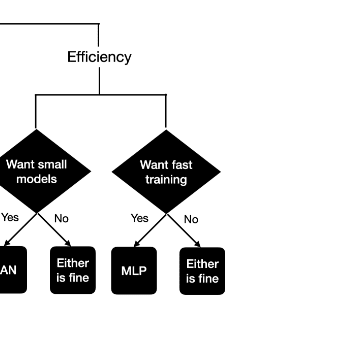
It seems like they mean faster per parameter, which is an... unclear claim given that each parameter or step, here, appears to represent more computation (there's no mention of flops) than a parameter/step in a matmul|relu would? Maybe you could buff that out with specialized hardware, but they don't discuss hardware.
One might worry that KANs are hopelessly expensive, since each MLP’s weight
parameter becomes KAN’s spline function. Fortunately, KANs usually allow much smaller compu-
tation graphs than MLPs. For example, we show that for PDE solving, a 2-Layer width-10 KAN
is 100 times more accurate than a 4-Layer width-100 MLP (10−7 vs 10−5 MSE) and 100 times
more parameter efficient (102 vs 104 parameters) [this must be a typo, this would only be 1.01 times more parameter efficient].
I'm not sure this answers the question. What are the parameters, anyway, are they just single floats? If they're not, pretty misleading.
100 times more parameter efficient (102 vs 104 parameters) [this must be a typo, this would only be 1.01 times more parameter efficient].
clearly, they mean 10^2 vs 10^4. Same with the "10−7 vs 10−5 MSE". Must be some copy-paste/formatting issue.
I'm guessing they mean that the performance curve seems to reach much lower loss before it begins to trail off, while MLPs lose momentum much sooner. So even if MLPs are faster per unit of performance at small parameter counts and data, there's no way they will be at scale, to the extent that it's almost not worth comparing in terms of compute? (which would be an inherently rough measure anyway because, as I touched on, the relative compute will change as soon as specialized spline hardware starts to be built. Due to specialization for matmul|relu the relative performance comparison today is probably absurdly unfair to any new architecture.)
Wow, this is super fascinating.
A juicy tidbit:
Catastrophic forgetting is a serious problem in current machine learning [24]. When a human masters a task and switches to another task, they do not forget how to perform the first task. Unfortunately, this is not the case for neural networks. When a neural network is trained on task 1 and then shifted to being trained on task 2, the network will soon forget about how to perform task 1. A key difference between artificial neural networks and human brains is that human brains have functionally distinct modules placed locally in space. When a new task is learned, structure re-organization only occurs in local regions responsible for relevant skills [25, 26], leaving other regions intact. Most artificial neural networks, including MLPs, do not have this notion of locality, which is probably the reason for catastrophic forgetting.
I mostly stopped hearing about catastrophic forgetting when Really Large Language Models became The Thing, so I figured that it's solvable by scale (likely conditional on some aspects of the training setup, idk, self-supervised predictive loss function?). Anthropic's work on Sleeper Agents seems like a very strong piece of evidence that it is the case.
Still, if they're right that KANs don't have this problem at much smaller sizes than MLP-based NNs, that's very interesting. Nevertheless, I think talking about catastrophic forgetting as a "serious problem in modern ML" seems significantly misleading
(likely conditional on some aspects of the training setup, idk, self-supervised predictive loss function?)
Pretraining, specifically: https://gwern.net/doc/reinforcement-learning/meta-learning/continual-learning/index#scialom-et-al-2022-section
The intuition is that after pretraining, models can map new data into very efficient low-dimensional latents and have tons of free space / unused parameters. So you can easily prune them, but also easily specialize them with LoRA (because the sparsity is automatic, just learned) or just regular online SGD.
But yeah, it's not a real problem anymore, and the continual learning research community is still in denial about this and confining itself to artificially tiny networks to keep the game going.
I'm not so sure. You might be right, but I suspect that catastrophic forgetting may still be playing an important role in limiting the peak capabilities of an LLM of given size. Would it be possible to continue Llama3 8B's training much much longer and have it eventually outcompete Llama3 405B stopped at its normal training endpoint?
I think probably not? And I suspect that if not, that part (but not all) of the reason would be catastrophic forgetting. Another part would be limited expressivity of smaller models, another thing which the KANs seem to help with.
So, after reading the KAN paper, and thinking about it in the context of this post: https://www.lesswrong.com/posts/gTZ2SxesbHckJ3CkF/transformers-represent-belief-state-geometry-in-their
My vague intuition is that the same experiment done with a KAN would result in a clearer fractal which wiggled less once training loss had plateaued. Is that also other people's intuition?
I know this sounds fantastic but can someone please dumb down what KANs are for me, why they're so revolutionary (in practice, not in theory) that all the big labs would wanna switch to them?
Or is it the case that having MLPs is still a better thing for GPUs and in practice that will not change?
And how are KANs different from what SAEs attempt to do
MLP or KAN doesn't make much difference for the GPUs as it is lots of matrix multiplications anyway. It might make some difference in how the data is routed to all the GPU cores as the structure (width, depth) of the matrixes might be different, but I don't know the details of that.
[This comment is no longer endorsed by its author]
ADDED: This post is controversial. For details see the comments below or the post Please stop publishing ideas/insights/research about AI (which is also controversial).
Abstract: