I recently started learning measure theory but had a pretty hard time finding real-world examples of the different measures. So this is a list of real-world examples of some different, common measures.

The count measure

If I have 4 apples, their count measure is 4. The count measure is just normal counting.

The Dirac measure

You are camping in a forest with some trees. You've set up your tent and it was a lot of work, so you're not going to move. It's daytime. The trees cast shadows, but the tree cover is sparse enough that there's still some sunlight that hits the ground. As the day goes on, the shadows move, at times covering your camp, at times leaving you in the sun. The dirac measure for whether a shadow is on your tent is something that outputs 1 when a shadow is on your tent, and 0 when there isn't a shadow on your tent.

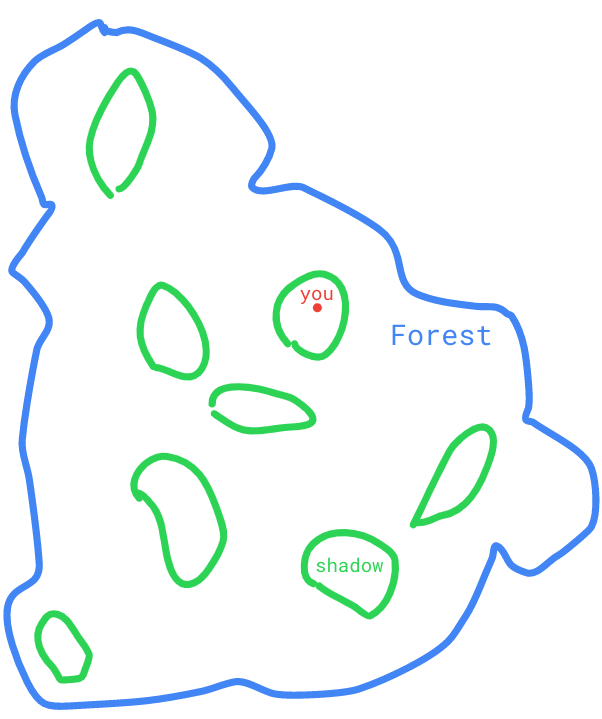
Formally, if ${\delta }_x$ means "Tent is in shadow", and A is the collection of shadow regions, the mathematical expression of this dirac measure is ${\delta }_x\left(A\right)=\{\begin{array}{c}0,x\notin A\\ 1,x\in A\end{array}.$ 

The dirac measure always looks like this, whatever meanings you attach to ${\delta }_x$ and the set A. 

(Since x is a point, the analogy breaks down a little: shadows are not allowed to partially overlap the tent. They cover it fully, or they don't touch it. We could fix this above by talking about "the northwesternmost atom of fabric of the tent" instead of "the tent").

(The dirac measure is similar to the indicator function (not measure!) $1_A\left(x\right)$, which takes a point $x$ and returns whether or not it's in A. For example, if you were walking around the forest instead of entented in it - that is, if the red point in the picture was moving around and the shadows didn't move, instead of the other way around - you could set up an indicator function $1_a\left(x\right)$ to be 1 when you're inside a shadow, and 0 when you're outside one. A previous version of this post confused the dirac measure with the indicator function; the difference is that ${\delta }_x$ takes a set A as input and assumes $x$ fixed, while $1_A$ takes a point $x$ as input and assumes the set A fixed. Thanks to deluks917 in the comments for the correction.)

The Lebesgue measure

The length of a line. The area of a flat shape. The volume of a 3D object. The equivalent concept in 4D, 5D, and so on. The name can be intimidating, but as a person in the physical world, you already have an intuitive idea of how the Lebesgue measure should work. 

An important feature of the Lebesgue measure ${\mu }_L$ is that if you move your set around, ${\mu }_L$ doesn't change. An orange has the same volume whether it's in my left hand, my right hand, or balanced on your head across the room from me. Also known as "translation invariance".

So far as I can tell, the Jordan measure and Borel measure are very similar to the Lebesgue measure, and as such I struggle to find real-world examples of them that explain how they are different from the Lebesgue. If someone puts intuitive examples of these in the comments, I’ll add them to this post.

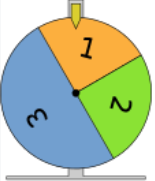
Probability measure

A probability measure ${\mu }_p$ is a measure that satisfies the usual requirements on a probability distribution: it's restricted to the range (0, 1), its sum over that range is 1, and it satisfies a condition called "countable additivity", which you probably don't have to think about too much.

Pictured is an example with ${\mu }_p\left(1\right)={\mu }_p\left(2\right)=\frac{1}{4};{\mu }_p\left(3\right)=\frac{1}{2}.$

Angle measure

A measure ${\mu }_{\circ }$ that sums to 360°. Pictured, ${\mu }_{\circ }\left(a\right)\approx {50}^{\circ };{\mu }_{\circ }\left(b\right)\approx 130°;{\mu }_{\circ }\left(c\right)={180}^{\circ }$.

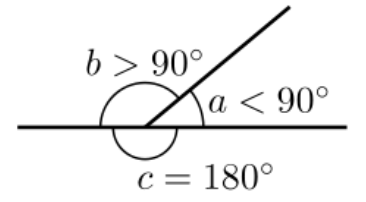
Angle measures are rotation invariant: rotate the picture above, and a, b, and c will still be the same angles. I think they're translation invariant, too? Seems like if you scoot that picture around, nothing changes, as long as you moved everything all at the same time.

There are more measures, but I don't understand them yet! 

Thanks to the Youtube channel The Bright Side Of Mathematics for getting me from knowing nothing to knowing something, when all the other expositions I found were too hard to understand.